
Preparing for advanced math assessments can be a challenging yet rewarding journey. Success depends on understanding key principles and mastering the skills needed to tackle various types of problems. With a clear focus and proper guidance, learners can build the confidence necessary to excel.
These evaluations often emphasize a wide range of mathematical concepts, from foundational operations to more intricate problem-solving techniques. Identifying patterns, interpreting data, and applying logic are central to achieving high scores.
By exploring carefully organized materials and practicing consistently, students can strengthen their understanding and approach these tests with a strategic mindset. Learning from detailed explanations and reviewing solutions is a proven way to enhance knowledge and improve results.
Understanding Algebra 2 Regents Exams
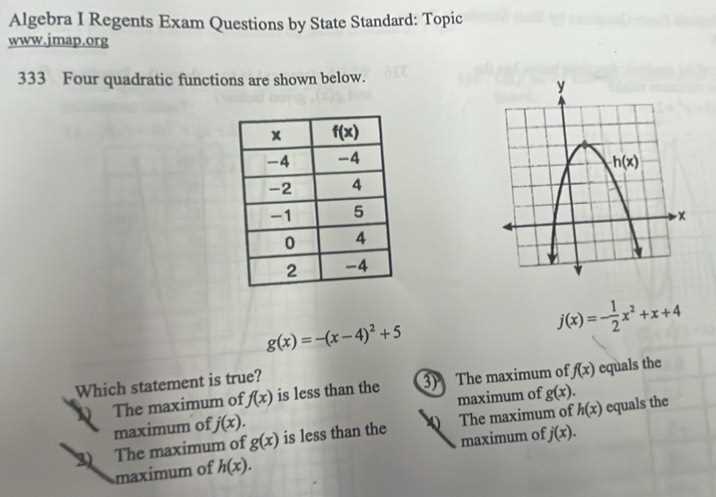
Advanced mathematics evaluations are designed to measure a student’s grasp of essential concepts and their ability to apply these principles in various scenarios. These assessments require critical thinking, problem-solving skills, and a solid understanding of mathematical foundations to navigate effectively.
The structure of these tests often includes a mix of problem formats, encouraging learners to demonstrate versatility in their methods. From calculating complex functions to interpreting data within real-world contexts, each section challenges students to think analytically and efficiently.
To excel, individuals should focus on familiarizing themselves with recurring problem types and practicing consistently. Reviewing detailed explanations of solutions can provide valuable insights into effective approaches, enhancing both accuracy and confidence.
Key Topics Covered in Algebra 2
Advanced mathematics courses often build upon foundational principles, introducing more complex ideas and methods to expand a student’s problem-solving capabilities. These areas of study are interconnected, creating a comprehensive understanding of mathematical relationships and applications.
- Equations and Inequalities: Developing skills to solve various forms of expressions, including linear, quadratic, and higher-order cases.
- Functions and Graphs: Exploring relationships between variables through visual representations and transformations.
- Polynomials and Factoring: Understanding the behavior of these expressions and mastering techniques to simplify and solve them.
- Exponential and Logarithmic Relations: Examining growth and decay models and their inverse operations.
- Data and Probability: Learning to analyze statistical information and calculate likelihoods for diverse scenarios.
By delving into these areas, students gain the tools to tackle a wide variety of challenges, preparing them for both academic assessments and real-world applications.
Breaking Down State Standards
Mathematical frameworks are designed to guide learning and ensure consistency across educational institutions. These frameworks outline essential concepts and skills, helping students build a strong foundation while preparing for advanced problem-solving tasks.
Core Objectives of Learning Guidelines
Learning objectives focus on equipping students with the ability to interpret patterns, apply logical reasoning, and analyze quantitative relationships. These goals emphasize not only procedural fluency but also a deeper understanding of how concepts interconnect.
Emphasis on Practical Applications
In addition to theoretical knowledge, the guidelines encourage applying mathematical principles to real-world scenarios. This includes understanding data trends, solving contextual problems, and making predictions based on numerical analysis, all of which reinforce critical thinking skills.
By understanding these educational frameworks, students can align their study plans with expected outcomes, ensuring a targeted and effective approach to mastering essential concepts.
How to Analyze Exam Questions
To effectively approach a test, it’s essential to break down each problem and understand what is being asked. Recognizing key details and determining the most appropriate method to solve the problem can make a significant difference in your ability to perform under time constraints. A thoughtful analysis ensures that all aspects of the problem are addressed efficiently and accurately.
By focusing on the core elements, you can avoid confusion and approach each task methodically. Identifying patterns, narrowing down the possible solutions, and organizing your thoughts will streamline the process and reduce the likelihood of making mistakes.
| Step | Action | Benefit |
|---|---|---|
| Read Carefully | Examine the problem to understand its requirements fully. | Provides clarity on what needs to be solved. |
| Identify Key Information | Highlight important data and conditions provided in the task. | Ensures focus on relevant details. |
| Choose an Approach | Determine the most effective method or formula to apply. | Increases efficiency and accuracy in solving. |
| Check the Solution | Review the calculations to confirm the result is correct. | Helps catch errors before finalizing the answer. |
By following these steps, you can develop a structured approach to solving problems and improve your overall performance in any assessment.
Common Problem Types in Algebra 2
Mathematical assessments often focus on a wide range of problem types designed to test a student’s understanding of key concepts and their ability to apply those concepts in different situations. Recognizing these common problem structures can help students prepare more effectively and tackle challenges with greater confidence.
Equations and Inequalities
Solving equations and inequalities forms a core part of many assessments. These problems require students to find unknown values by manipulating expressions, simplifying terms, and applying mathematical rules. Mastering linear, quadratic, and rational equations is essential for success.
Functions and Graphs
Problems involving functions often require students to work with equations that define relationships between variables. Graphing these functions, interpreting their behavior, and solving for specific values is a critical skill. Students are often asked to identify transformations, roots, and key features of the graphs.
Being able to identify these common problem types and understand the methods required to solve them enables students to approach their assessments strategically and improve their performance.
Tips for Solving Complex Equations
Solving intricate mathematical problems requires both strategy and precision. These types of problems often involve multiple steps and require a clear understanding of various concepts. By breaking down the problem and approaching it methodically, you can simplify even the most complex expressions.
Step-by-Step Approach
Start by carefully reading the problem and identifying what is being asked. Look for key elements such as unknown variables, constants, and any operations involved. Breaking the problem into smaller parts helps in understanding the structure and allows for more focused work.
Use of Mathematical Properties
Remember to apply fundamental mathematical properties, such as the distributive property, factoring, and combining like terms. These properties help simplify the equation and make it easier to solve step by step. Be sure to manipulate both sides of the equation consistently to maintain equality.
| Step | Action | Benefit |
|---|---|---|
| Isolate Variables | Move terms involving the unknown to one side. | Helps simplify the equation and makes solving more straightforward. |
| Combine Like Terms | Group similar terms to reduce complexity. | Reduces the number of terms and makes the equation easier to manage. |
| Check for Extraneous Solutions | Substitute the solutions back into the original equation. | Ensures the solutions are valid and do not introduce errors. |
With practice, these techniques can significantly improve your ability to solve complicated problems quickly and accurately, ensuring that you approach every equation with confidence.
Strategies for Graphing and Functions
Graphing and working with functions are essential skills that require both analytical thinking and visual interpretation. Understanding how to represent relationships between variables graphically helps clarify complex concepts and simplifies problem-solving. By applying systematic strategies, you can approach graphs and functions with greater ease and accuracy.
One of the key strategies is to begin by identifying the type of function you are dealing with. Linear, quadratic, exponential, and rational functions each have distinct characteristics that affect their graphs. Recognizing these characteristics will help you quickly sketch the graph and identify key features such as intercepts, slopes, and asymptotes.
Understanding Transformations is another important aspect of graphing. Shifting, stretching, and reflecting the graph of a basic function can help you visualize more complex relationships. These transformations affect the shape and position of the graph, so mastering them is crucial for accurate representation.
Working with Coordinates is a practical strategy when graphing. Plotting specific points based on the function’s equation allows you to visualize the overall shape of the graph. Start by finding key points such as intercepts and vertices, and then plot additional points to get a clearer picture of the graph’s behavior.
By combining these strategies, you can graph functions with confidence, interpret their behavior, and solve problems more effectively.
Mastering Polynomials and Rational Expressions

Polynomials and rational expressions are fundamental components of many mathematical problems. Mastering these concepts not only enhances your problem-solving skills but also prepares you for more advanced topics. By learning how to manipulate polynomials and simplify rational expressions, you can approach these problems with greater efficiency and confidence.
To begin with, understanding the basic structure of polynomials is essential. Polynomials consist of terms that are added or subtracted, with each term having a variable raised to a power. Recognizing the degree and coefficients of these terms will help you simplify and solve related problems.
Simplifying Polynomials
Simplifying polynomials involves combining like terms and applying the distributive property. This step is crucial for making the expression easier to work with. Here are a few strategies to simplify polynomials:
- Combine terms with the same variable and exponent.
- Distribute any constants or coefficients across terms.
- Factor expressions when possible to find common factors.
Working with Rational Expressions
Rational expressions are fractions that contain polynomials in both the numerator and denominator. Simplifying these expressions requires finding common factors and reducing the fraction. Key steps for working with rational expressions include:
- Factor both the numerator and denominator completely.
- Cancel any common factors between the numerator and denominator.
- Ensure that no division by zero occurs in the simplified expression.
By practicing these methods, you can master the art of simplifying and manipulating polynomials and rational expressions, making complex problems much more manageable.
Exploring Exponential and Logarithmic Problems
Exponential and logarithmic problems often present unique challenges due to their specific rules and properties. These types of equations and functions deal with rates of change, growth, and decay, which are commonly found in real-world applications. Understanding the relationship between exponential and logarithmic expressions can significantly improve problem-solving skills in various mathematical contexts.
Exponential functions involve a constant raised to a variable exponent, typically showing growth or decay. On the other hand, logarithmic functions are the inverse of exponential functions. By mastering the fundamental concepts and solving problems involving both, you can tackle complex mathematical challenges with confidence.
Solving Exponential Equations
To solve exponential equations, it’s important to isolate the exponential term and then apply logarithms or use properties of exponents. Here are some tips for solving these problems:
- Rewrite the equation in terms of a common base, if possible.
- Take the logarithm of both sides to simplify the equation.
- Use logarithmic properties such as the power rule to simplify further.
Working with Logarithmic Equations

Logarithmic equations often require the use of the properties of logarithms to simplify and solve. The goal is typically to isolate the logarithmic term and then exponentiate both sides to eliminate the log. Key strategies for solving logarithmic equations include:
- Combine logarithms with the same base using the product, quotient, or power rule.
- Exponentiate both sides to remove the logarithmic function.
- Check for extraneous solutions after solving the equation.
With practice, you can develop a strong understanding of how to approach both exponential and logarithmic problems, making them more accessible and easier to solve.
Essential Concepts in Probability and Statistics
Probability and statistics are two fundamental areas of mathematics that focus on data analysis and uncertainty. These concepts help us understand and predict outcomes in various real-world scenarios, from games of chance to analyzing patterns in large datasets. Mastering these areas enhances your ability to make informed decisions based on data and assess the likelihood of different events.
In probability, we calculate the likelihood of an event occurring, which can be represented as a value between 0 and 1. Statistics, on the other hand, focuses on collecting, analyzing, and interpreting data to uncover patterns and make predictions. These subjects are often intertwined and can be applied to a wide range of fields, including finance, healthcare, and social sciences.
Understanding Probability
Probability is the study of randomness and uncertainty, and it involves calculating the likelihood of various events. Here are some key points to remember when working with probability:
- The probability of an event is always between 0 and 1.
- To find the probability of independent events, multiply their individual probabilities.
- For mutually exclusive events, add their probabilities together.
Key Statistical Methods
Statistics involves several methods for analyzing and summarizing data. Some of the key concepts include:
- Mean: The average of a set of numbers, calculated by adding all values and dividing by the total number of values.
- Median: The middle value in a data set when arranged in ascending order.
- Mode: The value that appears most frequently in a data set.
By understanding these essential concepts, you can better analyze data and make more informed predictions and decisions based on probability and statistical analysis.
Preparing for Multiple-Choice Questions
When approaching multiple-choice assessments, it’s crucial to develop strategies that allow you to effectively evaluate each option and identify the correct answer. These types of questions often test your ability to apply knowledge quickly and accurately, making time management and careful analysis key components of success. Understanding common patterns in question structure can help you eliminate incorrect choices and increase your chances of selecting the right one.
One effective approach is to first read the question thoroughly to grasp what it’s asking. Afterward, carefully examine all available choices. Often, there will be one or more options that are clearly incorrect. Eliminating these options can significantly improve your odds, especially when you’re unsure of the answer. Additionally, look for clues within the question itself or in other related areas that may point toward the correct response.
Effective strategies for tackling multiple-choice questions:
- Read carefully: Ensure that you fully understand what the question is asking before considering the options.
- Eliminate wrong answers: Often, you can rule out one or more choices right away based on logical reasoning or obvious errors.
- Work through the problem: If possible, work through the math or logic of the question before looking at the options.
- Don’t second-guess: Trust your initial instinct unless you find clear evidence that suggests otherwise.
By mastering these strategies, you can improve your efficiency and accuracy when facing multiple-choice questions, increasing your confidence and performance on the test.
Best Practices for Open-Ended Problems
Approaching open-ended problems requires a strategic mindset and a methodical approach. Unlike multiple-choice questions, these problems demand that you not only find the solution but also clearly explain how you arrived at it. The focus should be on logical reasoning, step-by-step clarity, and a well-organized presentation of your thought process.
To effectively tackle these types of problems, begin by carefully reading the prompt to fully understand the task at hand. It’s important to identify all the given information and what is being asked before proceeding. Once you have a clear understanding of the problem, plan your approach and break it down into smaller, manageable steps. This approach will prevent errors and help maintain focus throughout the problem-solving process.
Tips for success with open-ended problems:
- Comprehend the problem: Take the time to read the entire prompt thoroughly and determine what is required for a solution.
- Organize your solution: Break the problem down into logical parts and solve each section step by step.
- Show all work: Always demonstrate each stage of your solution, explaining your reasoning at each step.
- Verify your solution: Once completed, review your work to confirm that all aspects of the problem have been addressed.
- Be concise yet clear: Provide a complete explanation, but avoid unnecessary elaboration. Focus on clarity and precision.
By following these best practices, you will be able to present well-organized, thoughtful solutions to open-ended problems, making it easier for others to follow your reasoning and ensuring that you’ve addressed all aspects of the challenge.
Utilizing Answer Keys Effectively
Answer keys can be a powerful tool in enhancing your understanding and reinforcing your learning. However, to maximize their benefit, it’s crucial to approach them strategically. Simply looking at the solution is not enough; it’s important to engage with the material actively and learn from the process, not just the final result. This method will help you improve your problem-solving skills and avoid making the same mistakes in the future.
Start by attempting each problem on your own before referring to the solution. This ensures that you’re practicing independently and challenging yourself. Once you’ve completed the problem, compare your approach to the one provided in the answer key. Look for any discrepancies in reasoning, and identify areas where your solution might differ from the correct one.
Tips for using answer keys effectively:
- Analyze the steps: Don’t just check if the answer matches; review the steps involved in reaching the solution. This will help you understand the logic and methods used.
- Identify mistakes: If your solution doesn’t match the key, try to pinpoint where you went wrong. Understanding your errors is key to preventing them in the future.
- Clarify confusion: If a step in the answer key is unclear, research or ask for clarification. It’s important that you understand each part of the solution.
- Practice similar problems: Use the answer key as a guide to solve similar problems. This helps reinforce the methods and concepts you’ve learned.
- Use it as a review tool: After you’ve learned the material, use the answer key to quickly review and reinforce key concepts before assessments.
By following these strategies, you’ll be able to use answer keys as a valuable resource for improving your problem-solving abilities and gaining deeper insights into the material.
Common Mistakes to Avoid on Exams
When preparing for any type of assessment, it’s crucial to be aware of common pitfalls that can negatively impact performance. These mistakes, often made in the heat of the moment, can be easily avoided with careful attention and a strategic approach. Recognizing and addressing these errors ahead of time will help you approach problems with confidence and precision.
Key mistakes to avoid:
- Rushing through problems: One of the most frequent errors is trying to complete tasks too quickly. While time management is important, rushing can lead to careless mistakes and missed details. Take your time to read and understand each question fully.
- Misinterpreting the question: Often, individuals misread or misunderstand the prompt, leading to incorrect approaches. Carefully examine each part of the problem to ensure you know exactly what is being asked before you start solving.
- Skipping steps: Skipping intermediate steps in your calculations or reasoning can cause you to overlook critical errors or miscalculate. Always show your work and document your thought process as you go through each step.
- Overlooking instructions: Some tasks may contain special instructions that significantly affect how to approach the problem. Always read the entire problem, including any instructions, before beginning your work.
- Failing to double-check answers: It’s easy to overlook small errors if you don’t review your work. After solving a problem, take a few moments to go back and ensure your solution makes sense and that all steps are correct.
- Being too reliant on shortcuts: While shortcuts can save time, relying too heavily on them without fully understanding the underlying concepts can lead to mistakes. Make sure you have a solid understanding of the methods before using shortcuts.
By being mindful of these common errors and practicing strategies to avoid them, you can improve your accuracy and overall performance on assessments.
Improving Test Performance with Practice
Consistent practice is one of the most effective ways to enhance performance in any assessment. By regularly working through problems, you not only reinforce your understanding but also become more adept at identifying patterns and solving challenges quickly and accurately. Practicing under test conditions further helps build confidence and reduces anxiety on the actual day.
Benefits of regular practice:
- Strengthens problem-solving skills: The more problems you tackle, the more comfortable you become with various approaches and techniques. This builds a strong foundation for efficiently solving a range of challenges.
- Familiarizes you with the format: Repeated exposure to the types of problems and the format of the assessment allows you to better understand what is expected. You will be able to anticipate the structure and plan your time more effectively.
- Increases speed and accuracy: Frequent practice allows you to sharpen your skills, enabling you to complete tasks more quickly and with fewer mistakes. This is especially valuable when time is limited during a test.
- Boosts confidence: As you solve more problems successfully, you gain greater confidence in your abilities. This positive mindset can make a big difference when tackling challenging problems during the test.
- Identifies areas for improvement: By practicing regularly, you can pinpoint areas where you may need further review. This allows you to focus your study efforts on specific areas of weakness, leading to more targeted improvement.
Make practice a part of your routine, setting aside time each day to work through different types of problems. Over time, you will notice a significant improvement in your ability to approach and solve challenges effectively.
Resources for Regents Exam Preparation
Preparing for a challenging assessment requires access to the right tools and materials. By utilizing various resources, learners can build their knowledge, practice essential skills, and develop effective strategies for success. A combination of study guides, practice tests, and instructional videos can help solidify understanding and improve performance.
Study Guides and Textbooks
Comprehensive study guides are essential for reviewing key concepts and theories. Many guides break down complex topics into smaller, manageable sections, making it easier to focus on specific areas that need improvement. Textbooks also serve as reliable references, offering detailed explanations and practice exercises.
Online Resources and Tutorials
In addition to traditional study materials, online platforms offer interactive learning opportunities. Websites, videos, and forums allow students to explore topics in greater depth, often providing step-by-step solutions to problems. These platforms also enable learners to ask questions and engage with peers and experts.
Helpful online resources:
- Interactive websites: Websites like Khan Academy or Coursera provide free courses and practice problems tailored to a variety of subjects.
- Video tutorials: Platforms like YouTube host channels dedicated to breaking down difficult concepts and offering visual explanations.
- Discussion forums: Online forums and study groups offer a collaborative space where students can share tips, discuss challenges, and get guidance from others.
By incorporating these resources into your preparation, you can improve your understanding, boost your confidence, and approach the assessment with a stronger foundation.