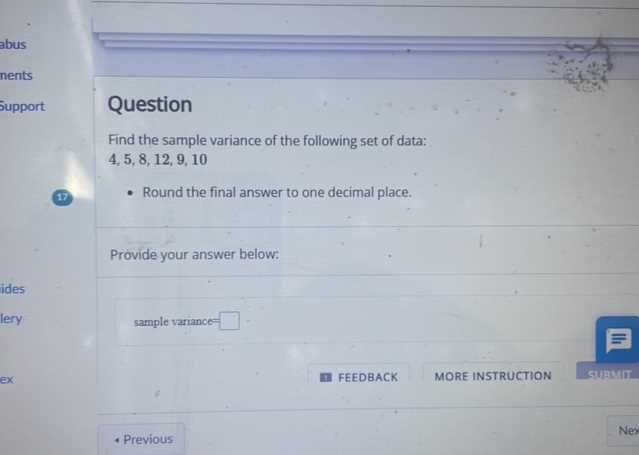
In statistics, measuring how data points differ from a central value provides valuable insights into the spread or dispersion within a dataset. This concept helps in assessing how consistent or varied the observations are. By calculating this measure, one can gain a deeper understanding of the underlying patterns in the data.
Precision plays a crucial role in conveying meaningful results. After calculating a measure of spread, it’s often necessary to express the outcome with a certain level of accuracy. This allows for easier interpretation while maintaining the integrity of the data’s significance.
In this section, we will explore methods to compute the degree of variability, followed by techniques to simplify the final outcome by limiting its complexity. This approach ensures both clarity and usefulness in real-world applications.
Understanding Variance and Its Importance
In data analysis, understanding how spread out or clustered values are around a central point is essential. This measure provides insight into the degree of variability within a set of data, highlighting whether the values are tightly grouped or dispersed. Knowing this is key to making informed decisions based on how predictable or fluctuating a dataset might be.
Significance of Spread in Data Analysis
A greater spread often indicates a higher degree of uncertainty or diversity within the dataset. On the other hand, a lower spread may suggest that the data points are more predictable and closely related. This concept is used across many fields such as finance, research, and quality control, where understanding the consistency of results is crucial.
Applications of Measuring Spread
Measuring how much data points deviate from an average value can assist in various practical scenarios. It can be used to assess risk in financial investments, quality control in manufacturing, or even to interpret scientific research results more effectively.
| Scenario | Use of Spread Measure |
|---|---|
| Finance | Assessing market risk and volatility |
| Manufacturing | Ensuring product consistency |
| Research | Evaluating experimental accuracy |
What Is Variance in Statistics
In statistical analysis, assessing how much data points differ from a central value is essential. This measure helps determine the degree to which individual values deviate from the mean, providing insight into the consistency or unpredictability of the dataset. It is a key concept used in various fields such as research, economics, and quality control.
Key Concept of Deviation
Deviation refers to the difference between each data point and the mean. By analyzing these deviations, one can understand the extent of variability within the dataset. A higher spread indicates more unpredictability, while a lower spread suggests that the values are more consistent and concentrated around the central value.
How It Relates to Other Statistical Measures
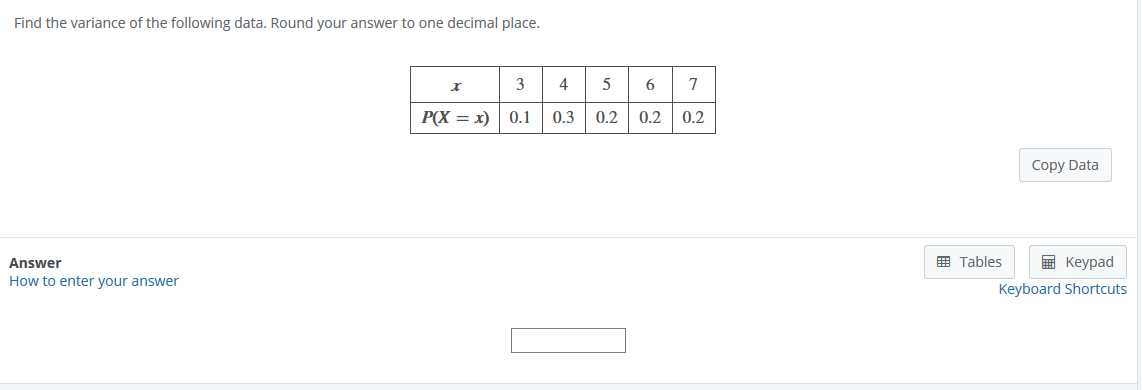
This measure is often used in conjunction with other statistical tools, such as standard deviation, to give a clearer picture of the dataset’s characteristics. While both tools assess spread, the measure discussed here focuses on the squared differences from the mean, making it particularly useful in various advanced analyses.
Key Concepts Behind Variance Calculation
To effectively assess the spread of data, it’s important to understand the underlying principles that drive the calculation process. This involves analyzing how each data point compares to a central value and measuring the differences. These differences are then used to provide a numerical representation of how widely values are distributed across the dataset.
Deviations and Squaring Differences
Each data point’s deviation from the mean is calculated first. This step measures how far each value is from the average. By squaring these differences, the negative values are eliminated, ensuring that all deviations contribute positively to the final result. This squaring process amplifies larger differences and ensures that they have a greater influence on the final result.
Importance of Averaging Squared Deviations
Once the squared differences are calculated, they are averaged to find the mean of squared deviations. This provides an overall measure of spread within the dataset, helping to determine how much variation exists in comparison to the average value. By averaging the squared deviations, one can assess the general level of fluctuation within the data, which is crucial for making informed conclusions.
How Variance Relates to Standard Deviation
Both of these statistical measures are used to evaluate the spread of data, but they provide different perspectives on how data points deviate from the central value. While both concepts are closely related, understanding their differences and how they complement each other is essential for a comprehensive analysis of data distribution.
Connecting the Two Measures
In simple terms, one measure is derived from the other. The measure of spread we’ve been discussing is first calculated, and then the standard deviation is obtained by taking the square root of this result. This relationship helps to simplify interpretation, as the standard deviation is expressed in the same units as the original data, while the spread measure involves squared units.
Key Differences and Uses
- Units: The standard deviation shares the same units as the data, making it more intuitive for practical interpretation.
- Interpretation: While both assess the degree of spread, the standard deviation is often preferred for comparing different datasets due to its direct relevance to the original values.
- Calculation: Calculating the standard deviation requires taking the square root of the measure of spread, simplifying the interpretation without altering the underlying information.
Both metrics are valuable tools in statistical analysis, with each offering a unique perspective on the data’s dispersion. The choice of which to use often depends on the context and the need for precision in interpretation.
Steps to Calculate Variance
To measure the spread of a dataset, there are several steps that need to be followed carefully. By breaking the process into manageable stages, it becomes easier to compute and understand how much the data points deviate from the central value.
Step-by-Step Process
- Step 1: Begin by calculating the mean of all data points. Add up all values and divide by the total number of observations.
- Step 2: Subtract the mean from each data point. This gives the deviation of each value from the central value.
- Step 3: Square each of the deviations. This eliminates any negative values and ensures that all deviations are treated equally.
- Step 4: Add up all the squared deviations to get a total sum.
- Step 5: Divide the sum of squared deviations by the total number of observations. This provides a measure of how spread out the data is.
Final Calculation
The final result reflects the degree of variation present in the dataset. While the process may seem detailed, breaking it down into smaller steps helps ensure accuracy and clarity when interpreting the dataset’s distribution.
Why Rounding Is Important in Statistics
In statistical analysis, precise calculations are crucial, but excessive precision can make results less practical and harder to interpret. Simplifying results through rounding helps improve clarity and enhances the ease of communication, making complex data more understandable for decision-making and reporting.
Benefits of Rounding in Data Analysis

- Simplification: Large numbers or long decimal strings can be overwhelming, and rounding makes the data more accessible for analysis and presentation.
- Consistency: Rounding helps ensure uniformity in reported figures, especially when data is presented in tables or graphs.
- Improved Interpretation: Rounded figures allow stakeholders to grasp key insights more quickly, without getting lost in unnecessary detail.
- Reduction of Errors: By reducing the number of digits, rounding minimizes the potential for errors that might arise when handling overly precise data.
When to Apply Rounding
In most statistical work, rounding is applied after all calculations are completed. This prevents introducing inaccuracies early on in the process. It is essential to choose an appropriate level of precision based on the context and the scale of the data being worked with.
Rounding Techniques for Statistical Answers
When presenting statistical results, the way numbers are simplified can affect both their clarity and precision. Various rounding methods are used to ensure that data remains accurate and easily interpretable, while minimizing the potential for confusion or errors in reporting.
Common Rounding Methods
- Rounding Up (Ceiling): This technique involves increasing the number to the nearest value when the digit after the rounding point is greater than or equal to five. It ensures that the result is always slightly higher than the original value.
- Rounding Down (Floor): The opposite of rounding up, this method reduces the number to the nearest value when the following digit is less than five, ensuring the result is slightly lower.
- Bankers’ Rounding: In cases where there’s a tie (i.e., the digit is exactly five), this technique rounds to the nearest even number, preventing cumulative rounding errors over multiple calculations.
- Truncation: Instead of rounding, truncation involves cutting off the digits after the rounding point, disregarding any remaining values without adjusting the number.
Choosing the Right Method

Deciding which rounding method to use depends on the context of the analysis and the level of precision required. For example, when working with financial data, bankers’ rounding may be preferred to avoid bias, while in scientific studies, a consistent approach might be needed for accuracy in reporting.
Common Errors in Variance Calculations
In statistical analysis, mistakes can easily occur during complex calculations. These errors can lead to incorrect conclusions and affect decision-making. Understanding common pitfalls is crucial for improving accuracy and reliability in results.
Typical Mistakes in Calculation
- Incorrect Mean Calculation: One of the most common mistakes is calculating the mean incorrectly. The mean serves as the foundation for all subsequent calculations, so errors at this stage propagate throughout the process.
- Failure to Square Differences: After finding the differences from the mean, they need to be squared. Some may forget this crucial step, leading to incorrect results.
- Using the Wrong Formula: Using a formula designed for a sample rather than a population (or vice versa) can result in misleading conclusions, as each method adjusts differently for sample size.
- Incorrectly Handling Negative Values: When dealing with negative differences from the mean, improper treatment of these values can lead to a biased or inaccurate outcome.
Preventing Calculation Errors
To avoid these errors, it’s important to double-check each step of the process. Ensuring that the proper formula is used, recalculating the mean, and confirming that all differences are squared correctly can significantly reduce the likelihood of mistakes.
Using Variance in Real-World Scenarios
Understanding how data points vary from a central tendency is vital in various fields. It allows individuals and organizations to assess the spread of information, predict outcomes, and make informed decisions based on statistical analysis. From finance to education, knowing how widely values fluctuate can help better understand patterns and risks.
Applications in Business and Finance
In finance, assessing risk is essential. Analysts use these measures to gauge the consistency of investment returns. High fluctuation values indicate high-risk investments, while low variability suggests stability. This insight helps investors make informed decisions about portfolio management and risk assessment.
Applications in Education and Research
In education, variability analysis is often used to understand the performance differences between students or groups. It helps educators identify areas where interventions may be necessary, and can also assist researchers in understanding the effectiveness of different teaching methods or interventions over time.
Variance in Different Data Sets
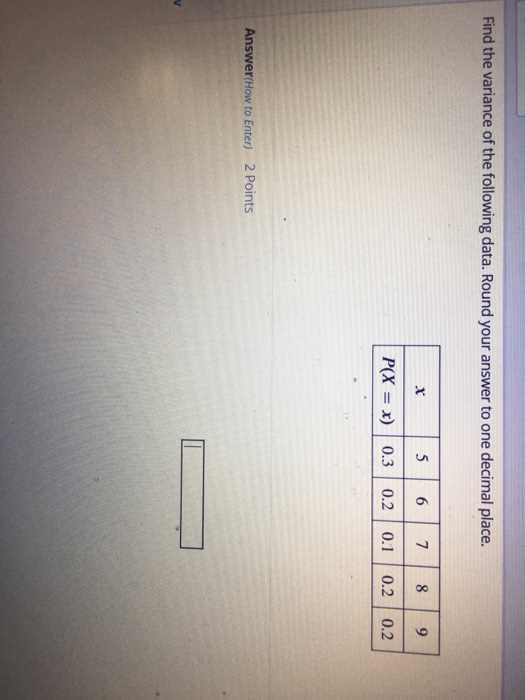
Data sets often present varying levels of consistency. The degree of spread between values can differ significantly depending on the nature of the data. Understanding these differences allows analysts to draw meaningful conclusions and apply appropriate methods for further analysis. By examining how values deviate within various data sets, it becomes easier to determine patterns, trends, and potential outliers.
For example, in financial markets, stock prices may exhibit high variability, reflecting fluctuating values influenced by market conditions. In contrast, data from a manufacturing process may show low variability, indicating consistent performance or product quality over time. Identifying these differences helps make informed decisions based on the data’s inherent characteristics.
How to Interpret Variance Results
Understanding the spread of data values is key to drawing meaningful conclusions. A higher result indicates greater variability, meaning the data points are more spread out from the average. On the other hand, a smaller value suggests that the data points are clustered more closely around the mean. Interpreting this spread helps in making decisions based on the reliability and consistency of the data set.
High vs. Low Variability
A larger result often points to greater uncertainty or inconsistency within the data. For instance, when analyzing test scores, a large result could indicate that students’ performances vary widely. Conversely, a smaller result suggests consistency, which could be seen in processes or operations with minimal fluctuation in results.
Contextual Analysis
Interpreting these results depends on the context in which the data is applied. In some fields, such as finance, higher variability may be expected and even desired, while in other areas, like quality control, low variability may be a sign of success and efficiency. Understanding what is considered “normal” variability in a particular field helps in making appropriate judgments.
Effect of Outliers on Variance
Outliers, or extreme values in a data set, can significantly influence the spread of values. When outliers are present, they can distort measures of variability, leading to misleading interpretations. These unusually high or low values pull the overall result further from the central tendency, causing an increase in the calculated spread. It’s important to recognize their impact when analyzing the consistency of data.
Impact on Statistical Measures
Increased variability often results from outliers because they create larger differences between the mean and the other data points. This leads to a skewed perception of data distribution. In cases where precision is important, such as quality control or financial forecasting, outliers can lead to errors in decision-making if not addressed appropriately.
Managing Outliers in Data Sets

To manage outliers effectively, analysts may choose to remove, adjust, or use robust statistical methods that minimize their effect. However, depending on the situation, outliers can also provide valuable insights into unique occurrences or rare events. Understanding when to include or exclude these points is essential for accurate analysis.
Calculating Variance for Population Data
In statistical analysis, determining the spread or variability of a full set of data points is crucial for understanding its distribution. When working with population data, every data point within the group is considered, and the calculations reflect the entire population’s dispersion. The method involves measuring how far each value deviates from the mean and then averaging those squared deviations.
Steps for Calculating Variability

To compute this measure for population data, begin by calculating the mean. Afterward, subtract the mean from each data point, square the result, and then sum these squared differences. Finally, divide the total by the number of data points in the population. This process yields a measure that captures the extent of spread within the entire group.
Key Considerations
Note: Unlike sample data, there is no need to adjust for a smaller sample size when working with population data. The result provides an accurate measure of how data points are distributed across the entire population without any scaling factors. Understanding these calculations is fundamental for any analysis that deals with complete groups, such as census data or exhaustive surveys.
Calculating Variance for Sample Data
When working with sample data, it is important to measure how much individual values deviate from the mean within a subset of a larger population. This calculation gives an understanding of the spread or dispersion of the sample. Since sample data represents only a part of the whole, adjustments are made to account for the smaller sample size.
Steps for Calculation
To calculate the dispersion for a sample, follow these steps:
- First, calculate the sample mean by summing all values and dividing by the number of sample points.
- Next, subtract the mean from each data point to find the deviations.
- Square each deviation to eliminate negative values and emphasize larger differences.
- Sum all squared deviations.
- Finally, divide this sum by the number of sample points minus one (this adjustment, known as Bessel’s correction, helps avoid bias in estimates).
Why the Adjustment Matters
For sample data, dividing by n-1 rather than n corrects for the fact that samples tend to underestimate variability. This correction ensures that the measure is a more accurate reflection of the larger population, especially when the sample size is small. By applying this approach, sample-based calculations become more reliable for making generalizations about the population from which the sample is drawn.
Why Round to One Decimal Place
In many cases, simplifying numerical results helps in making data easier to interpret and communicate. Precision is important, but in certain contexts, it can be overwhelming or unnecessary to present an excessive number of digits. Adjusting values to a single place after the decimal point strikes a balance between accuracy and clarity, making it more accessible without losing meaningful information.
When performing calculations or presenting data in fields such as statistics, rounding to one decimal place helps ensure that the results are both reliable and user-friendly. While more precision can be important in some advanced analyses, most real-world applications do not require extreme levels of detail. This approach improves consistency and enhances the readability of results, particularly when dealing with large datasets or communicating findings to a broad audience.
How Precision Affects Variance Results
Precision plays a crucial role in determining the outcome of statistical measures, especially when analyzing the spread of data. Small changes in the accuracy of data entries can significantly influence the overall calculations. The more precise the measurements, the more exact the results, but this can sometimes lead to complications when interpreting or simplifying findings. In cases where extreme accuracy isn’t necessary, focusing on a specific level of precision can help make the data more manageable and comprehensible.
When higher precision is used, each data point contributes a smaller error to the final calculation, resulting in a more detailed representation of variability. However, this can also introduce noise or unnecessary complexity, especially when the data isn’t significant to that level of accuracy. In practical applications, it is often a balance between detail and simplicity that leads to the most actionable insights, particularly when considering large datasets or when working within certain constraints.
Common Variance Misconceptions Explained
Many individuals often misunderstand key concepts related to the spread of data, leading to common mistakes in calculations and interpretations. These errors stem from a lack of understanding about the underlying principles and how subtle differences can affect results. It is essential to address these misconceptions to improve comprehension and application in real-world situations.
Misconception 1: Larger Values Always Mean Greater Spread
One of the most common misunderstandings is assuming that larger numbers automatically indicate a greater spread in data. In reality, spread is a measure of variability, not size. While large data values may appear to be more spread out, other factors, such as the presence of outliers or the central tendency of the data, can significantly impact this measure.
Misconception 2: Low Values Indicate Low Variability
Another frequent misconception is that low numerical results indicate low variability. This assumption overlooks how data points are distributed across a set. A low calculated result may still reflect a highly varied dataset if the values are not centered or spread evenly.
| Data Set | Spread (Variance) | Key Insight |
|---|---|---|
| 1, 1, 1, 1, 1 | 0 | All data points are identical, showing no spread. |
| 1, 5, 9, 13, 17 | 26.0 | Data is evenly spread out, leading to a higher result. |
| 5, 9, 15, 25, 45 | 212.5 | A significantly wider spread is observed, indicating a large variability. |
Practical Examples of Variance Calculations
Real-world scenarios often require calculating how spread out or dispersed data is from the average. Understanding this concept is vital for making decisions based on data analysis. Below, we explore several practical situations where these calculations help provide clearer insights into variability.
Example 1: Exam Scores
Consider a class of students who took a test, and their scores were as follows: 85, 90, 88, 92, 100. To understand the level of consistency or disparity in their performance, we can calculate how much each score deviates from the average score. A higher spread indicates greater variability in student performance.
Example 2: Daily Temperatures
Imagine a scenario where the daily temperatures of a city over a week are recorded as follows: 18°C, 20°C, 22°C, 23°C, 24°C, 19°C, 21°C. The purpose of this calculation is to understand how much daily temperatures fluctuate, which can be useful for energy consumption predictions or weather-related studies.
| Data Set | Average | Spread | Key Insight |
|---|---|---|---|
| 85, 90, 88, 92, 100 | 91 | 37.5 | Moderate spread of student performance. |
| 18, 20, 22, 23, 24, 19, 21 | 21.0 | 4.67 | Low spread, showing relatively consistent daily temperatures. |