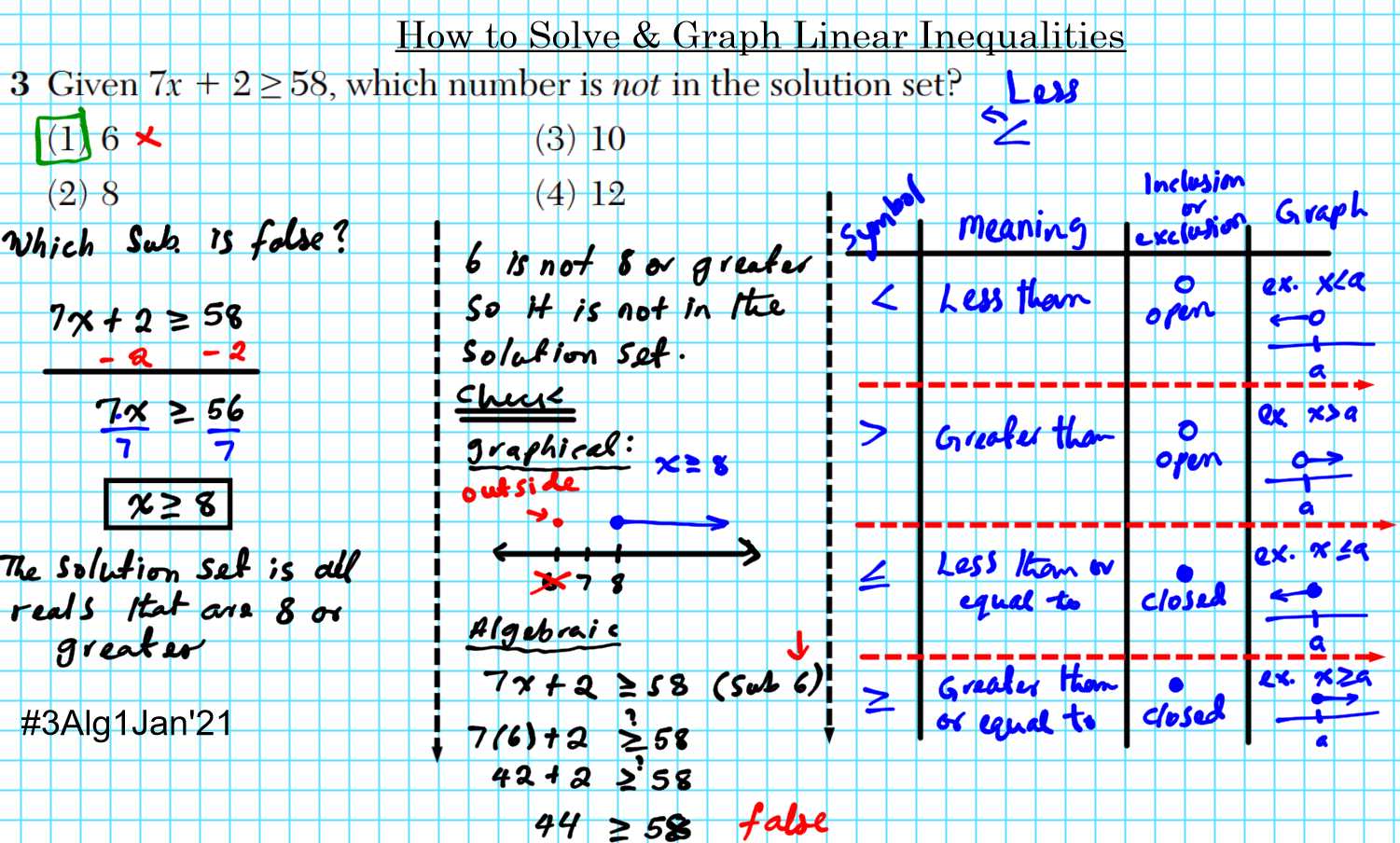
Preparing for standardized assessments requires a thorough understanding of problem-solving techniques and the ability to demonstrate the necessary steps. In this section, we provide detailed explanations and solutions to help students navigate through complex mathematical challenges effectively.
Step-by-step guidance is crucial to grasp the fundamental concepts and tackle each question with confidence. The solutions presented here include essential strategies to break down problems, ensuring clarity in every part of the process. Whether you’re looking to strengthen your skills or double-check your approach, these comprehensive methods will help you reach your goals.
Understanding how to present each solution clearly plays a significant role in achieving optimal results. By carefully analyzing each problem and its components, students can refine their technique and boost their chances of success. This resource serves as a valuable tool for anyone aiming to excel in their upcoming assessments.
Answer Key for the August 2025 Examination
This section provides a comprehensive guide to the solutions of the most recent exam, highlighting the key methods and techniques used to solve each problem. By following the step-by-step breakdowns, students can improve their understanding and enhance their problem-solving skills for similar future assessments.
Key Problem Solving Approaches
The focus is on presenting each solution in a clear and logical manner, allowing students to follow the reasoning behind every step. The examples provided cover a range of difficulties, offering practical insights into how to approach both straightforward and more complex questions.
Exam Solution Breakdown
The table below outlines the problem number along with the method used to arrive at the correct result. Each entry includes a summary of the approach, ensuring that learners can quickly review the steps involved.
| Problem | Method | Solution |
|---|---|---|
| 1 | Identify variables and apply distributive property | 4x = 12 |
| 2 | Use quadratic formula to solve | x = -2, 3 |
| 3 | Simplify expression using factoring | (x-5)(x+3) = 0 |
| 4 | Substitute values into equation and simplify | y = 7 |
| 5 | Graph and identify the intercepts | (0, -4), (2, 0) |
By reviewing each solution carefully, students can gain a deeper insight into the techniques used and prepare more effectively for their next challenge.
Overview of the Examination
This section provides an overview of the key elements and structure of the assessment, focusing on the essential concepts that students need to grasp in order to succeed. The test evaluates a range of mathematical skills, from foundational principles to more advanced problem-solving techniques. Understanding the format and expectations can help students approach the exam with confidence and clarity.
Test Format and Structure
The exam consists of multiple parts, each designed to assess different aspects of mathematical proficiency. The first section typically involves solving equations, simplifying expressions, and applying basic principles. Later sections may include more complex problems, such as systems of equations, functions, and data analysis, requiring a deeper understanding of the subject matter.
Key Areas of Focus
Students are expected to demonstrate their ability to tackle a variety of problems that test both their theoretical knowledge and practical application skills. Topics such as linear equations, inequalities, and graphing are commonly featured, alongside word problems and other real-world applications. The test is structured to assess not only knowledge but also the ability to logically approach and solve problems.
Important Topics Covered in the Examination
This section outlines the primary subjects assessed in the exam, highlighting the concepts that students should focus on to achieve success. The test evaluates a broad range of mathematical principles, each requiring both understanding and application to solve problems effectively. Mastery of these topics is essential for performing well in the assessment.
Key areas include solving linear and quadratic equations, analyzing functions, and working with systems of equations. Additionally, students must demonstrate proficiency in graphing, working with inequalities, and interpreting data. Understanding these core subjects will provide a strong foundation for tackling the exam’s diverse challenges.
Step-by-Step Solutions for Practice Questions
This section provides detailed instructions on how to approach and solve sample problems, breaking down each step to ensure a thorough understanding of the process. By following these stepwise solutions, students can grasp the logical approach needed to tackle similar problems effectively in their assessments.
Breaking Down the Problem
Each problem is explained through a series of logical steps, focusing on the application of key principles. These solutions are designed to enhance problem-solving skills, showing how to navigate through complex situations by breaking them into manageable parts.
Solutions Table
The table below outlines the approach and solution for each practice question, making it easier to follow the steps involved in reaching the correct outcome.
| Problem | Method | Solution |
|---|---|---|
| 1 | Solve using substitution method | x = 3, y = 4 |
| 2 | Factor the quadratic expression | (x – 2)(x + 5) = 0 |
| 3 | Graph and find the slope | Slope = 2 |
| 4 | Use the distributive property to simplify | 3x + 6 = 15 |
| 5 | Identify and solve the system of equations | y = 5, x = 1 |
By carefully reviewing these step-by-step explanations, students can develop a deeper understanding of problem-solving strategies and gain confidence in their ability to approach similar questions on their own.
Understanding the Grading System
The grading system for this exam is designed to assess not only the accuracy of responses but also the clarity and completeness of the solutions provided. Each part of the test contributes to the overall score, and students must meet specific criteria to achieve passing marks. Grasping how each component is scored is essential for maximizing performance on the assessment.
Score Breakdown
Understanding the weight assigned to each section can help students allocate their time and focus appropriately. The test is divided into multiple parts, each with a distinct point value:
- Multiple-choice questions: These questions test fundamental knowledge and are worth fewer points than the open-ended sections.
- Short-answer questions: Students must show their reasoning to earn full credit for these questions.
- Extended-response questions: These require a detailed explanation of the problem-solving process and are worth the most points.
Scoring Criteria
The grading process takes into account several factors to ensure fairness and consistency:
- Accuracy: Correct solutions are necessary for the highest scores.
- Clarity of steps: Clear and logical presentation of each step is essential.
- Completeness: Solutions must be fully explained, not just a final answer.
By understanding how each question is evaluated, students can better focus on presenting their solutions in a clear, concise manner, ensuring they meet all necessary criteria for a high score.
How to Approach Complex Problems
When faced with intricate questions, it’s essential to break them down into smaller, more manageable parts. This approach helps to simplify the problem-solving process and ensures that no steps are overlooked. By focusing on each element individually, students can build confidence and increase their chances of reaching the correct solution.
Step-by-Step Problem Solving
The first step is to carefully read through the problem and identify what is being asked. Look for key information, such as variables, numbers, and relationships between elements. Once this is understood, the next step is to outline a plan or strategy for tackling the problem. Start with the most straightforward elements, and gradually address the more complex aspects as you progress.
Utilizing Logical Reasoning
Logical reasoning plays a vital role in solving more advanced problems. As you work through the question, consistently check that each step flows logically from the previous one. If any part of the solution seems unclear, take a moment to re-evaluate the approach and adjust your strategy. This methodical approach will help you avoid mistakes and improve accuracy in your solutions.
Common Mistakes in the Exam
When preparing for the exam, it’s important to be aware of common errors that can affect performance. These mistakes often arise from a lack of attention to detail, misunderstandings of key concepts, or failure to follow through with all the required steps. Recognizing and addressing these pitfalls can significantly improve your chances of success.
One of the most frequent errors involves rushing through problems, leading to simple calculation mistakes or skipped steps. Another common issue is misinterpreting the question, which can result in an incorrect approach to the solution. Additionally, students often overlook the importance of organizing their work, which can make it difficult to identify and correct mistakes later on.
By being mindful of these common mistakes and adopting careful, methodical strategies, students can better navigate the challenges of the assessment and achieve more accurate results.
Time Management Tips for Exam Day
Effective time management is crucial during an exam, as it allows students to carefully allocate time to each section, ensuring that all questions are addressed. Without proper planning, it’s easy to run out of time or rush through questions, leading to unnecessary mistakes. By managing your time wisely, you can complete the exam confidently and thoroughly.
Prioritize the Easy Questions
Start by quickly scanning the entire test and identifying the questions you feel most comfortable with. Begin with these to build confidence and gain some momentum. This strategy ensures that you secure points from the easier questions before tackling the more difficult ones, leaving you with more time to focus on complex problems.
Set Time Limits for Each Section
Divide the total exam time by the number of sections or problems and set a strict time limit for each. Stick to these limits to avoid spending too much time on any one part. If you get stuck on a question, move on and come back to it later if time allows. This approach helps maintain a steady pace and ensures you complete all parts of the exam.
Best Resources for Exam Preparation
Having the right tools and materials for exam preparation can make all the difference in achieving success. From practice tests to instructional videos, there are numerous resources available that can help students strengthen their understanding and improve their problem-solving skills. These resources offer different approaches to learning, catering to various study preferences and needs.
Study Guides and Textbooks are essential for reviewing core concepts. Comprehensive guides break down topics step by step, making them ideal for reinforcing foundational knowledge. Look for those that include both examples and practice questions to test your understanding.
Online Practice Tests provide a realistic preview of what to expect on exam day. These tests help simulate the time constraints of the actual exam, allowing you to practice managing your time effectively. Many websites offer free or paid practice exams that mirror the format and difficulty level of the real test.
Video Tutorials are an excellent option for visual learners. Websites like YouTube offer a wealth of free educational content, explaining concepts in different ways and showing detailed solutions to common problems. These videos can clarify difficult topics and provide additional examples to reinforce learning.
Study Groups offer a collaborative environment where you can discuss difficult concepts, share strategies, and learn from peers. Being part of a study group can provide motivation and accountability while allowing for different perspectives on problem-solving techniques.
How to Interpret Exam Questions
Being able to accurately understand and interpret questions is a critical skill when taking any exam. Often, the wording of a question can be tricky, and it’s important to identify exactly what is being asked. A clear understanding of the question ensures that you approach each problem correctly, leading to more precise solutions and higher scores.
Key Strategies for Interpreting Questions
Here are several approaches that can help you better understand and tackle exam questions:
- Read the question carefully: Avoid rushing through the text. Take the time to read each question thoroughly, paying attention to key words and instructions.
- Identify what is being asked: Focus on the main task of the question. Look for action words such as “solve,” “simplify,” or “find the value.” These indicate what is required.
- Highlight important details: Mark any numbers, variables, or relationships that are crucial to solving the problem. This helps you stay organized and ensures no information is missed.
Common Pitfalls and How to Avoid Them
Sometimes, exam questions can be misleading or unclear. Here are some common mistakes and how to prevent them:
- Overlooking negative signs: Always double-check your calculations, especially when dealing with negative numbers or fractions. A small mistake in sign can lead to the wrong answer.
- Misunderstanding the question’s context: Ensure that you grasp the overall context of the problem before diving into solving. Take a moment to think about what the question is really asking.
- Skipping steps: Avoid jumping to conclusions. Write out each step of your solution to prevent missing any crucial parts of the process.
By following these strategies and avoiding common mistakes, you’ll be better prepared to tackle questions confidently and accurately. Interpreting each question correctly will allow you to approach the problem-solving process in a structured way, increasing your chances of success.
Significance of Showing Your Solution Process
In any problem-solving scenario, demonstrating the steps taken to arrive at a solution is just as important as the final answer itself. Clearly showing the solution process not only helps to validate the answer but also provides insight into how well the problem was understood. This is essential, especially in exams where partial credit may be awarded for correct reasoning, even if the final result is incorrect.
Why Showing Your Process Matters
Here are some key reasons why it is crucial to showcase your method of solving a problem:
- Clarifies Your Thought Process: Writing down each step ensures that your reasoning is clear and organized. It allows you to trace your logic and easily identify any mistakes.
- Demonstrates Understanding: Even if the final answer is wrong, showing the steps can demonstrate that you understood the concept and applied the right method.
- Earn Partial Credit: In cases where the final result is incorrect, examiners can award points for correct procedures, making it vital to show every step taken to solve the problem.
Common Mistakes to Avoid When Showing Your Work
While it’s important to show your solution process, it’s equally important to avoid common pitfalls that can make your solution unclear or incomplete:
- Skipping Steps: Don’t skip intermediate steps, even if they seem simple. Each step is crucial for clarity and accuracy.
- Illegible Writing: Ensure that your handwriting is neat and legible. If the examiner cannot read your work, they cannot evaluate it accurately.
- Failure to Label: Always label your variables and solutions clearly. Not doing so can make your solution confusing or hard to follow.
By carefully documenting each stage of your solution, you not only improve your chances of receiving partial credit but also demonstrate a deeper understanding of the material. The process itself is a reflection of your grasp of the concepts, and presenting it well is key to achieving the best results.
Techniques for Solving Word Problems
Word problems often present challenges because they require translating a narrative into a mathematical process. To tackle these effectively, it is essential to approach the problem systematically, breaking down the information provided and transforming it into solvable components. Developing a methodical approach will help make even the most complex scenarios more manageable.
Step-by-Step Approach to Word Problems
Here are key techniques to help you solve word problems with confidence:
- Read the Problem Carefully: Start by reading the problem multiple times. Ensure you understand what is being asked before proceeding. Focus on identifying the key pieces of information such as quantities, relationships, and the question itself.
- Identify the Variables: Assign variables to unknown quantities. These might be numbers or items that you need to solve for. Labeling these variables will help you organize your work and avoid confusion.
- Set Up an Equation: Once you have identified the variables, think about the mathematical relationships between them. Translate the information into an equation or system of equations that you can work with.
Common Strategies for Word Problems
Beyond the basic approach, several strategies can help you tackle more complicated problems:
- Draw a Diagram or Model: For some problems, a visual representation can make the relationships clearer. Draw a picture or create a table to organize the data and better understand the problem.
- Look for Patterns: Some word problems involve patterns or sequences. Identifying a pattern can help you create an equation or formula to solve the problem.
- Check Your Solution: Once you have found a solution, take the time to plug it back into the original problem to ensure it makes sense and answers the question correctly.
By following these techniques, you’ll be better equipped to navigate and solve word problems, making even the most complex situations more manageable. Remember, practice and a step-by-step approach are key to mastering this skill.
Key Formulas to Remember for Algebra
When tackling mathematical problems, having a strong grasp of essential formulas is crucial. These formulas provide the necessary foundation for solving a wide range of problems efficiently. Whether working on basic equations or more complex scenarios, knowing these key relationships can help simplify the process and ensure accuracy.
Basic Operations and Properties
These fundamental formulas are used frequently in solving a variety of problems:
- Distributive Property: a(b + c) = ab + ac – This principle is essential for expanding expressions and simplifying terms within parentheses.
- Exponent Rules:
- a^m * a^n = a^(m+n) – When multiplying powers with the same base, add the exponents.
- (a^m)^n = a^(m*n) – When raising an exponent to another power, multiply the exponents.
- Square of a Binomial: (a + b)^2 = a^2 + 2ab + b^2 – Used for expanding binomial expressions and simplifying quadratic terms.
Solving Equations and Functions
These formulas are essential for solving equations and working with different types of functions:
- Slope of a Line: m = (y2 – y1) / (x2 – x1) – A critical formula for finding the slope between two points on a line.
- Quadratic Formula: x = (-b ± √(b² – 4ac)) / 2a – This formula is fundamental for solving any quadratic equation in standard form.
- Distance Formula: d = √((x2 – x1)² + (y2 – y1)²) – Useful for calculating the distance between two points on the coordinate plane.
Mastering these formulas is key to improving problem-solving efficiency and building confidence in mathematical applications. Regular practice will help reinforce these concepts and improve speed in tackling complex problems.
Reviewing Solutions with Detailed Explanations
Understanding how to approach and solve problems is just as important as knowing the final result. Breaking down solutions step by step allows for a deeper understanding of the methods used and helps identify any potential errors. By reviewing solutions thoroughly, you can strengthen your problem-solving skills and ensure you are fully prepared for similar challenges in the future.
When reviewing a solution, it is important to not only focus on the correct outcome but also examine the reasoning behind each step. This allows you to gain insight into the logic that drives each operation, whether it’s simplifying an expression or applying a formula. By understanding the process, you build the ability to approach problems from different angles, which is vital for tackling more complex scenarios.
Here’s how you can approach a detailed review:
- Start with the first step: Understand why each operation is performed and how it moves you closer to the solution.
- Identify key concepts: Each problem usually involves a set of rules or principles. Make sure you understand these before continuing.
- Double-check calculations: Ensure every computation is correct, as small errors can lead to incorrect final results.
- Understand intermediate steps: Break down complex steps into simpler parts to ensure clarity at every stage.
By reviewing solutions in this manner, you can develop a thorough understanding of each problem type and sharpen your problem-solving abilities. A detailed explanation ensures that not only the solution is achieved but also that the process is fully comprehended.
How to Check Your Work Effectively
Reviewing your solutions is a crucial step in ensuring the accuracy and correctness of your results. Effective verification goes beyond just scanning the final answer; it involves carefully retracing your steps and rethinking the approach. By checking your methods and calculations, you not only confirm your results but also reinforce your understanding of the problem-solving process.
The process of checking can be broken down into several strategies. First, go over each step methodically, ensuring that every operation was performed correctly. Pay attention to the logical flow and make sure that each decision was based on sound principles. After this, verify your final result through different methods, such as estimating or using an alternative approach. The goal is to build confidence in your solution while identifying any potential errors before submitting your work.
Steps to Effectively Verify Your Solutions
- Review the problem: Begin by reading the problem again to ensure you haven’t overlooked any important details or misinterpreted the instructions.
- Recheck calculations: Go over each mathematical operation, checking for any small errors like misplacing a decimal or making an incorrect sign change.
- Use estimation: Quickly estimate the expected result and compare it to your final answer to see if they align reasonably.
- Test your result: If possible, use an alternative method to solve the same problem and check if the results match.
Why Checking Matters
Effective checking allows you to catch mistakes early, reducing the risk of overlooking errors that could impact your final results. It not only ensures accuracy but also boosts your confidence in the solutions you present. By regularly practicing effective checking, you develop a strong habit that can be applied to a variety of problems, making you a more reliable and efficient problem solver.
Final Tips for Success
As the exam day approaches, it is essential to focus on refining your skills and enhancing your confidence. A combination of effective preparation, smart strategies, and a calm mindset can significantly impact your performance. In this section, we will highlight some final tips to ensure you are fully equipped for success when tackling the test.
Preparation and Strategy
- Review key concepts: Make sure to revisit essential topics and formulas. Having a strong grasp of core principles will help you navigate more challenging questions.
- Practice regularly: The more problems you solve, the better you will become at recognizing patterns and applying techniques efficiently.
- Simulate real test conditions: Take practice tests under timed conditions to build stamina and get accustomed to working within time limits.
- Prioritize weak areas: Identify topics that you find difficult and focus extra time on practicing those areas to build confidence.
Mindset and Exam Day Tips
- Stay calm: Manage anxiety by practicing relaxation techniques. A calm mind is essential for clear thinking during the exam.
- Read questions carefully: Take the time to understand what each question is asking before jumping into solving it.
- Show all your steps: Demonstrating your thought process can not only help in catching mistakes but may also earn you partial credit if the final answer is incorrect.
- Manage time wisely: Allocate enough time for each section and avoid spending too much time on one question. If you’re stuck, move on and come back to it later.
By following these strategies, staying focused, and applying your knowledge confidently, you can maximize your chances of performing well. Success is the result of consistent effort and a positive mindset. Best of luck!
Frequently Asked Questions about the Exam
Preparing for any assessment can raise a number of questions. It’s normal to feel uncertain about various aspects of the exam, whether it’s about the structure, timing, or specific strategies to succeed. In this section, we will address some common concerns and provide clarity to help you approach the test with confidence.
General Exam Information
- What is the format of the test? The exam typically consists of multiple-choice questions, short answer problems, and extended response sections. It’s designed to assess your understanding and application of key mathematical concepts.
- How long is the test? The duration of the exam generally ranges from two to three hours, depending on the specific requirements. You’ll have a set time limit to complete all questions, so managing time effectively is crucial.
- Can I use a calculator? Yes, calculators are usually permitted for certain sections of the test. However, it’s important to know which type of calculator is allowed and which sections require manual calculations.
Preparation Tips
- How should I prepare for the exam? Review key topics, practice problems, and take simulated tests. Focus on understanding the underlying concepts rather than just memorizing procedures. Consistent practice will help you identify areas of strength and weakness.
- Should I focus more on practice or theory? Both are important. It’s essential to have a solid understanding of the theory, but applying that knowledge through practice problems helps reinforce learning and improves problem-solving speed.
- What should I do if I don’t know how to solve a problem during the test? If you’re stuck, don’t panic. Try to break the problem into smaller steps or look for familiar patterns. If needed, move on to the next question and come back later if you have time.
After the Exam
- How long does it take to get results? The results are typically released a few weeks after the exam. This can vary depending on the testing agency and grading process.
- What happens if I don’t pass? If you do not achieve the required score, you may have the opportunity to retake the exam. Check the guidelines for retaking the assessment and prepare accordingly.
By addressing these frequently asked questions, we hope to ease any concerns and help you feel more prepared as you approach your upcoming test. Remember, preparation and a clear understanding of what to expect are key to success.