
Understanding the dynamics of how substances interact and transform during reactions is a fundamental aspect of studying reaction rates. This section focuses on essential concepts, from basic principles to advanced mechanisms that dictate the speed and outcome of various processes. The goal is to equip you with the knowledge necessary to approach related problems effectively.
Grasping the factors influencing how quickly reactions occur can significantly enhance your ability to solve related challenges. You’ll explore various factors, such as temperature, concentration, and catalysts, that impact how fast a reaction progresses. These concepts are vital for predicting and controlling the outcomes of reactions in real-world scenarios.
Mastering the key equations and methods used to measure and analyze the rate of reactions is crucial. Understanding how to apply these techniques will allow you to break down complex reactions into simpler, manageable steps, paving the way for greater success in solving practical problems related to reaction rates.
Chemical Kinetics Exam Questions and Answers
When studying the principles that govern the speed and efficiency of reactions, it is important to understand the theoretical and practical aspects that influence these processes. This section is designed to help you reinforce key concepts by providing challenges and solutions, making complex topics more accessible. The objective is to build confidence and improve problem-solving skills related to reaction rates and their governing laws.
Understanding Reaction Rates
One fundamental concept is determining the rate at which a reaction occurs. Various factors such as temperature, pressure, and the presence of catalysts play a role in influencing the speed of reactions. It is essential to be able to analyze experimental data and derive the rate laws that describe how these factors affect the reaction. By practicing problems that involve rate determination, you can develop a deeper understanding of the relationship between reactant concentration and time.
Advanced Problems and Solutions

For more complex scenarios, problems may require applying integrated rate laws, half-life calculations, or interpreting reaction mechanisms. These challenges often involve multiple steps and a combination of different techniques. Solving such problems will require a firm grasp of both theoretical principles and practical skills, helping to ensure accurate predictions and understanding of the behavior of different reactions under varying conditions.
Basic Concepts of Chemical Kinetics
Understanding the principles that govern the speed and mechanisms of reactions is essential for predicting and controlling outcomes in various processes. This section delves into foundational ideas such as how reactions progress, what influences their rate, and how to measure these changes. A strong grasp of these concepts will provide the necessary tools for analyzing more complex scenarios.
| Term | Description |
|---|---|
| Reaction Rate | The speed at which reactants are converted into products over time. |
| Concentration | The amount of reactant present in a given volume, which can affect the rate of a reaction. |
| Activation Energy | The minimum energy required for molecules to collide and react. |
| Temperature | A factor that increases the energy of molecules, often leading to faster reactions. |
| Catalysts | Substances that increase the rate of a reaction without being consumed in the process. |
These key terms are the building blocks for exploring the various factors that affect how and why reactions occur at different rates. By studying these concepts, one can gain insights into optimizing processes in both laboratory and industrial settings.
Rate Laws and Reaction Orders

The relationship between the concentration of reactants and the speed at which a reaction occurs is fundamental to understanding how reactions proceed. By defining how changes in reactant concentration affect the reaction rate, one can predict and control outcomes more accurately. This section focuses on rate laws and the concept of reaction orders, which provide a quantitative framework for analyzing reaction behavior.
Understanding Rate Laws
Rate laws describe how the rate of a reaction depends on the concentration of the reactants. These laws are often determined experimentally and provide the mathematical relationship between the concentration of each reactant and the rate at which the reaction progresses. For many reactions, the rate law is expressed as: Rate = k[A]^m[B]^n, where k is the rate constant, and m and n are the orders with respect to each reactant.
Reaction Orders and Their Implications
Reaction order refers to the power to which the concentration of a reactant is raised in the rate law. It indicates how sensitive the rate of reaction is to changes in the concentration of a particular reactant. For example, a first-order reaction has a rate that is directly proportional to the concentration of one reactant, while a second-order reaction depends on the square of the concentration. Understanding these orders helps in predicting how the rate will change under varying conditions.
Factors Affecting Reaction Rates
The speed at which a transformation occurs can be influenced by a variety of factors. Understanding these influences is key to controlling or predicting how reactions unfold. This section examines the most important elements that impact the rate of a process, such as temperature, concentration, and the presence of catalysts.
Temperature and Reaction Speed
Temperature plays a significant role in determining how fast a transformation proceeds. As temperature increases, the energy of the particles involved also rises, leading to more frequent and energetic collisions. This generally results in a faster reaction rate. The relationship between temperature and rate can be quantified using the Arrhenius equation, which shows how the rate constant changes with temperature.
The Role of Concentration
The concentration of reactants is another critical factor. Higher concentrations typically lead to an increased frequency of collisions between molecules, thus accelerating the rate at which reactions occur. This is particularly evident in reactions where the rate is directly proportional to the concentration of one or more reactants. By adjusting the concentration, the speed of the reaction can be controlled.
Understanding Activation Energy
The rate at which a transformation occurs is not solely dependent on the reactant concentration or environmental conditions; it is also influenced by the energy required for the process to begin. This energy barrier, known as activation energy, must be overcome for a reaction to proceed. Understanding this concept is essential for controlling and optimizing reaction speeds in various settings.
What is Activation Energy?
Activation energy refers to the minimum energy required to initiate a reaction. It represents the energy needed to break bonds in the reactants so that new bonds can form to produce the products. If the reactants lack sufficient energy, they will not react, even if the conditions are otherwise favorable. The lower the activation energy, the faster the reaction tends to be.
Factors Influencing Activation Energy

- Temperature: Higher temperatures provide more energy to reactants, making it easier to overcome the activation energy barrier.
- Catalysts: Catalysts lower the activation energy by providing an alternative reaction pathway, thus speeding up the process without being consumed.
- Concentration: Higher concentrations of reactants increase the likelihood of collisions, potentially providing the energy needed to surpass the activation barrier.
By understanding and manipulating activation energy, reactions can be optimized for desired outcomes, making it a critical factor in both laboratory and industrial applications.
Arrhenius Equation Explained

The relationship between the rate of a reaction and temperature is a key factor in understanding how processes unfold. The Arrhenius equation provides a mathematical framework for quantifying this relationship, helping to explain why reactions proceed faster at higher temperatures. This equation links the rate constant of a reaction to both temperature and activation energy, offering insights into reaction behavior under varying conditions.
The Structure of the Equation
The Arrhenius equation is expressed as: k = A * e^(-Ea/RT), where k is the rate constant, A is the frequency factor (pre-exponential factor), Ea is the activation energy, R is the universal gas constant, and T is the temperature in Kelvin. This equation shows how the rate constant changes with temperature and provides a way to predict reaction rates under different conditions.
Key Variables and Their Roles
- Activation Energy (Ea): The energy barrier that must be overcome for the reaction to occur. A higher activation energy means the reaction will be slower at a given temperature.
- Frequency Factor (A): This factor reflects the number of successful collisions between reactants. It is a measure of the likelihood that reactants will come together in the correct orientation to react.
- Temperature (T): As temperature increases, the rate constant increases, as more molecules have the necessary energy to overcome the activation energy barrier.
By using the Arrhenius equation, one can estimate how temperature variations affect reaction rates and better understand the underlying principles governing chemical processes.
Methods for Determining Reaction Rate
Measuring the speed at which a transformation occurs is essential for understanding the underlying mechanisms and controlling the outcome of processes. Several techniques can be used to determine how quickly a reaction proceeds, each offering insights into different aspects of the reaction. This section explores some of the most commonly employed methods for monitoring and calculating reaction rates.
Common Techniques for Measuring Reaction Rates
- Concentration Measurements: This method involves monitoring the concentration of reactants or products over time. By measuring how the concentration changes, one can determine the rate at which the reaction occurs. Techniques such as spectrophotometry or titration are often used for this purpose.
- Gas Volume Measurement: For reactions that produce gas, measuring the volume of gas released can help determine the reaction rate. This method is useful for reactions that involve the formation of gaseous products, and it is typically done using a gas syringe or an inverted burette.
- Change in Mass: In reactions where solids are involved, monitoring the change in mass over time can provide information about the reaction rate. This technique is particularly useful for reactions that produce or consume solids.
- Temperature Monitoring: Since the rate of many reactions is temperature-dependent, measuring the temperature change over time can offer insights into the speed of the reaction. This can be done using thermometers or thermocouples.
Selecting the Right Method
The choice of method depends on the type of reaction and the available equipment. For example, reactions that produce gas can be efficiently monitored using volume measurement, while reactions in solution are often best analyzed through concentration measurements. By selecting the appropriate technique, one can accurately determine the rate and gain a deeper understanding of the reaction’s behavior under various conditions.
Elementary Reactions and Their Rates
In the study of reaction rates, it is crucial to understand the simplest forms of reactions, known as elementary processes. These reactions involve a direct interaction between reactant molecules, and their rate laws can often be derived from the stoichiometry of the reaction. This section delves into the basics of elementary reactions and how their rates are determined.
Understanding Elementary Reactions
Elementary reactions are those that occur in a single step, where reactant molecules collide and react directly to form products. The rate law of such reactions can be directly linked to the number of molecules involved in the process. These reactions are fundamental building blocks for more complex reactions and are essential for understanding reaction mechanisms.
Rate Laws of Elementary Reactions
- Unimolecular Reactions: In a unimolecular reaction, a single reactant molecule undergoes a transformation. The rate law for such a reaction is first-order, meaning that the rate depends on the concentration of just one reactant.
- Bimolecular Reactions: These reactions involve two reactant molecules colliding to form products. The rate law is second-order, as the reaction rate depends on the concentration of two reactants.
- Termolecular Reactions: Although less common, termolecular reactions occur when three molecules collide in a single step. The rate law is third-order and depends on the concentrations of three reactants.
The rate of elementary reactions is typically straightforward to calculate, as it directly reflects the stoichiometry of the reaction. By understanding these basic processes, one can build a more comprehensive picture of how complex reactions unfold over time.
Mechanisms of Complex Reactions
In many processes, reactions occur in multiple steps, involving a series of intermediate stages before reaching the final products. These complex transformations are known as reaction mechanisms. Understanding how a reaction unfolds step by step provides insight into the factors that influence its rate and the pathway it follows. This section explores the key aspects of reaction mechanisms and their importance in determining the outcome of a reaction.
Complex reactions often consist of multiple elementary steps, each of which can have its own rate law. By studying the sequence of these steps, one can deduce the overall reaction rate and identify the slowest step, known as the rate-determining step. This step typically controls the speed of the entire reaction, much like a bottleneck restricts the flow in a system.
Another important feature of complex reactions is the formation of intermediates. These are temporary species that are produced in one step and consumed in another. Although intermediates do not appear in the final products, they play a crucial role in facilitating the transformation of reactants into products.
Collision Theory and Reaction Rates

The fundamental principle behind how reactions occur lies in the interactions between particles. For a reaction to take place, the reacting molecules must collide with sufficient energy and proper orientation. This concept is captured by the collision theory, which helps explain the factors that influence how fast a reaction proceeds. By understanding the conditions under which effective collisions occur, one can gain insights into the speed and efficiency of a reaction.
According to the collision theory, not all collisions between reactants result in a successful reaction. Only those collisions that involve particles with sufficient energy–called activation energy–lead to the formation of products. Additionally, the orientation of the particles during the collision plays a critical role in whether the collision results in a transformation.
Key Factors Affecting Reaction Rates
| Factor | Effect on Reaction Rate |
|---|---|
| Temperature | Increasing temperature provides more energy to the reacting particles, increasing the number of collisions that have sufficient energy to result in a reaction. |
| Concentration | Higher concentration of reactants leads to more frequent collisions, increasing the likelihood of successful reactions. |
| Surface Area | A larger surface area allows more particles to collide at once, increasing the frequency of effective collisions. |
| Catalysts | Catalysts lower the activation energy required for a reaction, allowing more collisions to result in a successful transformation without being consumed in the process. |
By applying the collision theory, one can predict how changes in temperature, concentration, and other factors affect the speed of a reaction. This theory is essential for understanding and controlling the conditions under which chemical processes take place.
Catalysis in Chemical Reactions
In many reactions, the presence of certain substances can significantly speed up the process without being consumed in the reaction itself. This phenomenon is known as catalysis, and the substances that facilitate it are called catalysts. These agents work by lowering the energy barrier required for the reaction to occur, allowing the transformation to proceed more rapidly and efficiently. Understanding catalysis is essential in both industrial applications and laboratory processes.
Catalysts provide an alternative pathway for the reaction, one that requires less energy to reach the transition state. By doing so, they increase the frequency of successful collisions between reactants, leading to an overall faster reaction rate. However, despite participating in the reaction, catalysts remain unchanged at the end, which means they can be used repeatedly.
There are two main types of catalysis: homogeneous and heterogeneous. In homogeneous catalysis, the catalyst is in the same phase as the reactants, usually in a liquid or gas phase. In heterogeneous catalysis, the catalyst is in a different phase, typically a solid, while the reactants are in a liquid or gas phase. Both types of catalysis are widely used in various industries, from petroleum refining to pharmaceuticals.
By utilizing catalysts, industries can enhance reaction rates, reduce energy costs, and improve overall efficiency, making catalysis a cornerstone of modern chemical processes.
Determining Half-Life of Reactions
One of the key aspects of understanding the rate at which a reaction proceeds is the concept of half-life. This term refers to the time required for half of the reactants to be transformed into products during a reaction. It is a useful measure, particularly for reactions that occur at a constant rate, as it allows scientists to predict how long it will take for the reaction to reach a certain point. By determining the half-life, researchers can gain insights into the speed and behavior of reactions under various conditions.
The half-life of a reaction depends on the order of the reaction. For reactions that follow first-order kinetics, the half-life is independent of the initial concentration of reactants. In contrast, for second-order reactions, the half-life is inversely proportional to the concentration of reactants. Understanding these relationships allows chemists to tailor reaction conditions to achieve desired results more efficiently.
For example, in first-order reactions, the half-life (t₁/₂) can be calculated using the following equation:
t₁/₂ = 0.693 / k
where k is the rate constant. This formula illustrates that, for first-order reactions, the half-life remains constant regardless of the concentration of the reactant. In second-order reactions, the half-life is given by:
t₁/₂ = 1 / (k[A])
where [A] is the concentration of the reactant at the start. As the concentration decreases, the half-life increases.
By calculating and analyzing the half-life of reactions, scientists can gain a deeper understanding of the reaction mechanism and its efficiency, as well as make informed decisions about how to optimize reactions in both laboratory and industrial settings.
Integrated Rate Laws for Reactions
Understanding the relationship between the concentration of reactants and time is essential for predicting the behavior of a reaction as it progresses. Integrated rate laws provide a way to express this relationship mathematically, allowing us to track how the concentration of reactants changes over time. These laws are derived from the basic rate laws and offer a deeper understanding of how reactions unfold under different conditions.
For reactions of different orders, the integrated rate laws take different forms. They allow us to calculate the concentration of reactants at any given time during the reaction, which is crucial for determining how long it will take to reach a particular concentration or to complete the reaction entirely. Below, we will discuss the integrated rate laws for zero-order, first-order, and second-order reactions.
Zero-Order Reactions
In zero-order reactions, the rate of reaction is constant and does not depend on the concentration of reactants. The integrated rate law for a zero-order reaction is:
[A] = [A]₀ – kt
where [A]₀ is the initial concentration of reactant, k is the rate constant, and t is the time. This equation shows that the concentration of reactant decreases linearly over time, meaning that as the reaction progresses, the concentration diminishes at a constant rate.
First-Order Reactions

For first-order reactions, the rate is directly proportional to the concentration of one reactant. The integrated rate law for a first-order reaction is:
ln([A]₀ / [A]) = kt
or alternatively:
ln([A]) = ln([A]₀) – kt
Here, the natural logarithm of the concentration is plotted against time, yielding a straight line. This behavior indicates an exponential decrease in the concentration of reactant over time, which is characteristic of first-order reactions.
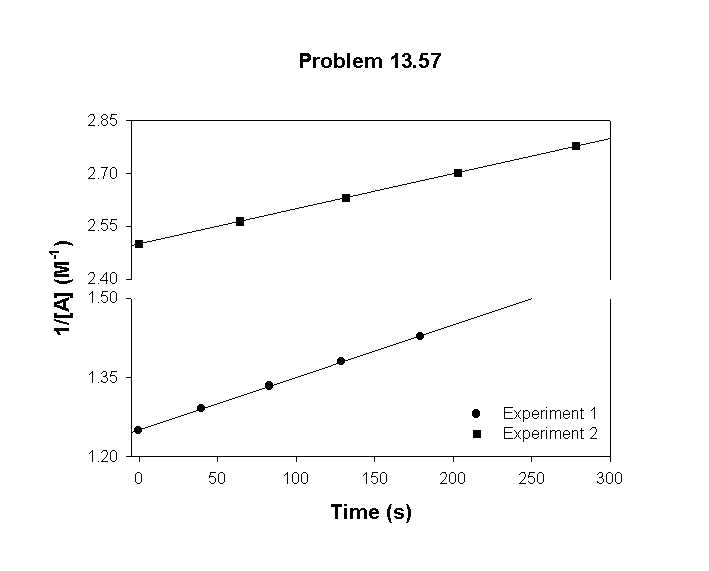
Second-Order Reactions

Second-order reactions are characterized by a rate that is proportional to the square of the concentration of a single reactant, or to the product of the concentrations of two reactants. The integrated rate law for a second-order reaction is:
1 / [A] = 1 / [A]₀ + kt
This equation shows that the inverse of the concentration increases linearly with time, meaning that as the reaction progresses, the concentration of reactant decreases more slowly compared to first-order reactions.
By using the integrated rate laws, scientists can predict the behavior of reactions over time, determine reaction rates, and plan experiments more effectively. These laws are essential tools for studying the dynamics of reactions in both laboratory and industrial settings.
Effect of Temperature on Reactions

Temperature plays a crucial role in determining the speed at which a reaction occurs. In general, increasing the temperature results in an increased rate of reaction, while decreasing the temperature slows down the process. This is because temperature influences the energy of molecules, which affects their ability to collide and react. As temperature rises, molecules move faster, and the frequency and energy of collisions increase, leading to a higher probability of successful reactions.
The relationship between temperature and reaction rate can be described through various principles and equations, such as the Arrhenius equation. Understanding this relationship is important for controlling reaction rates in industrial processes, chemical manufacturing, and laboratory experiments.
Temperature and Collision Frequency
At higher temperatures, molecules move more rapidly. As a result, they collide more frequently, which increases the chances of a successful reaction. The increased collision frequency contributes to a higher reaction rate, especially when reactants require a certain amount of energy to break bonds or form new ones. Key factors include:
- Increased molecular speed: Molecules move faster at higher temperatures, leading to more frequent collisions.
- Higher energy collisions: Molecules have more energy, increasing the likelihood that collisions will overcome the activation energy barrier.
Activation Energy and Temperature
The energy required for a reaction to occur, known as activation energy, can also be affected by temperature. As temperature increases, a greater proportion of molecules have enough energy to overcome the activation energy barrier. This explains why reactions typically speed up at higher temperatures. The relationship between temperature and activation energy can be described by the following:
- Lower activation energy threshold: More molecules possess the necessary energy to react when the temperature is higher.
- Arrhenius equation: This equation shows how the rate constant increases with temperature, further emphasizing the role of temperature in reaction rates.
In practical terms, understanding the effect of temperature on reactions is essential for optimizing reaction conditions in various applications, such as manufacturing, catalysis, and environmental management.
Experimental Methods in Kinetics
To understand how reactions occur and at what rates, various experimental methods are employed to collect data and analyze the process. These techniques allow scientists to determine important factors such as reaction speed, the effect of different variables, and the mechanism of the reaction. By observing the concentration of reactants or products over time, researchers can deduce how fast a reaction takes place and how it responds to changes in temperature, pressure, and other conditions.
Different experimental approaches are used to measure reaction rates, each suited to specific types of reactions and conditions. Some methods are based on monitoring the concentration of substances, while others focus on the physical properties of the system. Below are some commonly used techniques:
Monitoring Concentration Changes
One of the most straightforward ways to study reaction rates is by observing how the concentration of reactants or products changes over time. This can be done using various methods:
- Colorimetry: This technique measures changes in color during a reaction. The intensity of color can be directly related to the concentration of a substance in solution.
- Conductivity Measurement: If the reaction involves ions, changes in electrical conductivity can be monitored to follow the progress of the reaction.
- Spectrophotometry: By measuring the absorption or transmission of light through a sample, the concentration of reacting species can be tracked.
Measuring Physical Changes
In some reactions, physical changes such as pressure or volume variations can provide insight into the reaction rate. These methods are particularly useful for reactions involving gases or changes in the volume of a system. Some key techniques include:
- Pressure Measurement: For gas-phase reactions, changes in pressure over time can be used to determine the rate of reaction, especially when the volume is held constant.
- Gas Collection: Gases produced during a reaction can be collected and measured, providing a direct way to monitor the progress of the reaction.
- Temperature Measurement: Changes in temperature can also give clues about reaction rates, especially if the reaction is exothermic or endothermic.
These methods, combined with appropriate data analysis, provide critical information for understanding how reactions proceed under different conditions, helping to predict outcomes and optimize processes.
Applications of Chemical Kinetics
The study of how fast reactions occur and the factors influencing these rates plays a crucial role in numerous scientific and industrial fields. Understanding the dynamics of processes is vital for optimizing reactions, designing new materials, improving efficiency, and ensuring safety. From the development of pharmaceuticals to the optimization of industrial processes, the knowledge gained from studying reaction rates has far-reaching implications.
Below are some areas where the principles of reaction rates are applied to enhance technology, production, and safety:
Industrial Applications
In industrial settings, reaction rates are crucial for maximizing product yields and minimizing waste. Some key uses include:
- Pharmaceutical Manufacturing: The rate of reactions is critical in drug synthesis to ensure high efficiency and consistent quality. Understanding the mechanisms allows for better control over production processes and the design of more effective medicines.
- Petrochemical Industry: The optimization of reactions in refining processes, such as cracking and distillation, is essential for improving energy output and reducing operational costs.
- Food Industry: Reaction rates affect food preservation, fermentation, and the production of flavors. Monitoring these processes helps improve safety and quality while extending shelf life.
Environmental Impact
Understanding the rate of reactions is also vital for managing environmental impacts. Some key applications include:
- Pollution Control: Knowledge of how pollutants break down over time allows for the development of more efficient cleanup methods and sustainable environmental practices.
- Climate Change Studies: Reaction rates are important for understanding the formation and breakdown of greenhouse gases, helping predict and mitigate environmental changes.
Table: Examples of Applications in Different Fields
| Field | Application | Impact |
|---|---|---|
| Pharmaceuticals | Drug synthesis optimization | Improved efficiency, quality control |
| Petrochemicals | Fuel production and refining | Increased energy output, cost reduction |
| Environmental Science | Pollutant breakdown and remediation | Faster cleanup, less environmental damage |
By applying these principles, industries and researchers can not only enhance efficiency but also reduce costs, mitigate environmental impacts, and contribute to innovations that drive progress in multiple fields.
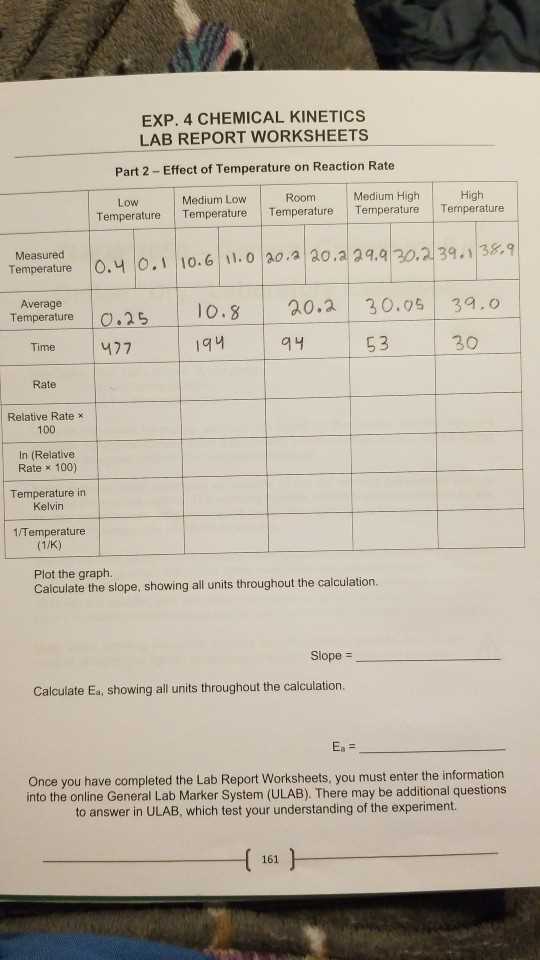
Common Mistakes in Kinetics Problems
When solving problems related to reaction rates and the factors influencing them, it’s easy to overlook key concepts or misapply certain principles. These mistakes can lead to incorrect conclusions or poorly designed experiments. Identifying these common errors is essential for improving problem-solving skills and achieving more accurate results.
Below are some of the frequent mistakes made when dealing with problems in this area:
- Misunderstanding Reaction Order: One common error is incorrectly determining the order of the reaction based on experimental data. It’s crucial to use the right method, such as the method of initial rates or integrated rate laws, to find the correct order. Skipping this step can lead to wrong calculations of rate constants.
- Assuming Constant Temperature: Reaction rates are highly sensitive to temperature. Assuming a constant temperature without considering its effect on the reaction rate can lead to inaccurate results, especially in cases where temperature changes are involved.
- Overlooking Units: It’s easy to forget about the proper units for rate constants, especially when using integrated rate laws. Inconsistent or incorrect units can lead to confusion and incorrect interpretations of data.
- Ignoring the Effect of Concentration: Many problems involve changes in concentration over time, but neglecting how concentration affects the rate can lead to incomplete or incorrect solutions. Always ensure the concentration is appropriately accounted for, particularly when dealing with complex reactions.
- Incorrectly Applying the Arrhenius Equation: The Arrhenius equation is used to relate reaction rates to temperature, but applying it incorrectly or failing to consider the correct parameters can lead to errors in predicting how the rate will change with temperature.
By being aware of these common mistakes, you can refine your approach to solving problems and avoid errors that might otherwise hinder your understanding of reaction mechanisms and their rates.