
Understanding the fundamentals of optimization models is crucial for anyone seeking to solve complex decision-making problems. These models often involve finding the best possible outcome within a given set of limitations, balancing various factors to achieve optimal results. Whether you’re studying for an assessment or simply looking to improve your skills, mastering the concepts and techniques is key to success.
Key methods such as graphical analysis, the simplex approach, and duality theory play a vital role in solving these problems efficiently. They help in navigating through variables, constraints, and objective functions, making sense of real-world scenarios like resource allocation, production planning, and cost minimization.
In this guide, we will explore practical examples, common challenges, and essential strategies for tackling optimization models. You’ll gain the insights needed to approach these problems confidently and effectively, ensuring you’re well-prepared for any related tasks or assessments.
Optimization Models and Solution Techniques
When faced with decision-making problems that involve maximizing or minimizing certain outcomes, a systematic approach is essential. Understanding how to break down the problem into manageable components, identify constraints, and define the objective is the first step toward finding the best possible solution. These types of problems are common in various fields such as business, economics, and engineering.
There are a variety of methods used to solve these challenges, ranging from basic graphical techniques to more advanced algorithms. Each method is suited for different scenarios, allowing for the identification of optimal solutions within the given limits. Familiarity with these approaches not only helps in solving practical problems but also in preparing for related evaluations.
In this section, we’ll explore common problems and how to approach them, providing detailed solutions and insights into effective problem-solving strategies. You will learn how to handle typical cases you may encounter, along with the rationale behind each step, helping you to develop a deeper understanding of the process.
Key Concepts in Optimization Models
At the core of solving optimization problems lies the ability to clearly define the components that influence the outcomes. This involves identifying objectives, constraints, and decision variables, each of which plays a critical role in determining the solution. Gaining a strong understanding of these basic elements is essential to navigating more complex scenarios effectively.
Objective Functions and Constraints
The objective function represents the goal of the problem, whether it’s maximizing profits, minimizing costs, or achieving another desired outcome. Constraints, on the other hand, define the limitations or restrictions that must be adhered to. Together, these two components shape the framework of the problem and guide the search for the optimal solution.
Decision Variables and Feasible Region
Decision variables are the elements you can control within the problem, typically representing quantities such as units produced, resources allocated, or time spent. The feasible region is the set of all possible solutions that satisfy the constraints. It’s within this region that the optimal solution must lie, and understanding its boundaries is crucial to solving the problem efficiently.
Understanding Objective Functions
The objective function serves as the foundation of any optimization problem, representing the outcome that needs to be maximized or minimized. Whether the goal is to maximize revenue, minimize expenses, or optimize another key performance indicator, this function quantifies the central aim of the problem. By analyzing it, one can direct efforts towards achieving the best possible result within given constraints.
Formulating the Objective Function
To formulate an objective function, it is essential to first understand the variables that influence the desired outcome. These variables are often linked to quantities like resources, time, or production levels. Once identified, the relationship between these variables is expressed in a mathematical form, enabling the model to compute the optimal solution based on the available data.
Maximization vs. Minimization
Depending on the problem’s nature, the objective function may either be maximization or minimization. In a maximization scenario, the goal is to increase the value of the objective, such as maximizing profits or production efficiency. In contrast, minimization problems aim to reduce costs or resource usage, striving for the lowest possible value within the constraints.
Defining Constraints and Variables
In optimization problems, defining the key elements that shape the solution is essential. These elements, namely the variables and constraints, determine the boundaries within which the solution must be found. Variables represent the controllable factors in the problem, while constraints set the limitations or restrictions that cannot be violated. Together, they form the framework that guides the search for an optimal outcome.
Understanding Decision Variables
Decision variables are the components of the problem that can be adjusted to achieve the desired objective. These variables often represent quantities such as the amount of resources used, the number of units produced, or the time allocated to a task. The challenge lies in selecting values for these variables that lead to the best possible outcome, while satisfying all constraints.
Setting Constraints and Boundaries
Constraints are conditions or restrictions that must be respected when solving the problem. They may arise from physical limits, such as the maximum capacity of a factory or the availability of resources. Alternatively, they can represent business rules or operational limits, like budget constraints or minimum production requirements. These boundaries ensure that the solution is both feasible and practical.
Graphical Method for Solving Problems
The graphical method is a visual approach to solving optimization problems with two variables. By plotting constraints and the objective function on a coordinate plane, this method allows for a clear representation of feasible solutions and helps identify the optimal point. It is especially useful for problems with simple, linear relationships between variables.
To effectively apply the graphical method, follow these steps:
- Plot the constraints: Each constraint is represented as a line on the graph. The region that satisfies all constraints is called the feasible region.
- Plot the objective function: Draw the line representing the objective function for a given value. Then, move the line to maximize or minimize the function, depending on the problem.
- Identify the optimal solution: The optimal solution lies at a corner point of the feasible region, where the objective function achieves its maximum or minimum value.
This method offers a straightforward way to visually identify the optimal solution, but it becomes less practical when dealing with more than two variables. Nonetheless, for simpler cases, it remains an effective tool for understanding the relationship between variables and constraints.
Simplex Method Step-by-Step
The simplex method is a powerful algorithm used to solve optimization problems, particularly those with multiple variables and constraints. It works by iterating through different feasible solutions until the optimal solution is found. The process involves moving from one corner point of the feasible region to another, improving the objective function at each step, until no further improvement can be made.
Step 1: Set Up the Initial Tableau
The first step in using the simplex method is to set up the initial tableau, which includes the objective function and the constraints. This tableau is a matrix that will be used to perform calculations in the subsequent steps. The tableau format allows for easy manipulation of the coefficients and helps track the progress toward the optimal solution.
| Basic Variables | Coefficients | RHS (Right-Hand Side) |
|---|---|---|
| Variable 1 | Value | Value |
| Variable 2 | Value | Value |
| Objective Function | Value | Value |
Step 2: Pivot and Improve the Solution

Once the initial tableau is set up, the algorithm proceeds by identifying the pivot element. The pivot element is selected based on the need to improve the objective function. By performing a series of row operations, the tableau is updated, and the process continues with each iteration. The goal is to move toward an optimal solution where no further improvements are possible.
Through these steps, the simplex method systematically narrows down the feasible region and identifies the best solution that meets all constraints.
Duality Theory in Optimization Models
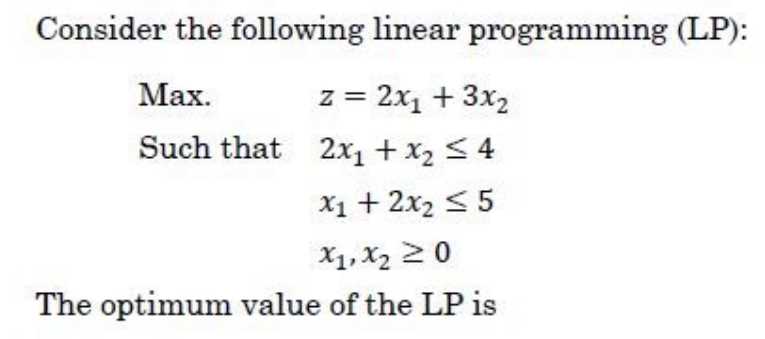
Duality theory provides a powerful framework for understanding the relationship between two interdependent optimization problems: the primal and the dual. This concept offers a way to view a given problem from two perspectives, highlighting how solutions to one problem can offer valuable insights into the other. The theory not only helps in solving complex problems but also provides deeper economic and practical interpretations of the problem’s structure.
Primal and Dual Problems
The primal problem represents the original optimization task, typically involving the maximization or minimization of an objective subject to certain constraints. The dual problem, on the other hand, is derived from the primal, with its own objective function and constraints. Interestingly, solving the dual problem can often lead to solutions that are as effective as solving the primal problem directly.
Duality Theorems and Economic Interpretation
Duality theory is governed by key theorems that establish a connection between the solutions of the primal and dual problems. One of the most significant results is the weak duality theorem, which states that the value of the objective function for the dual problem is always a bound for the primal problem. Furthermore, strong duality asserts that under certain conditions, the optimal values of the primal and dual problems are equal. This relationship offers valuable insights, especially in economics, where the dual variables can represent shadow prices or the value of additional resources.
Integer Programming Challenges and Solutions
Solving optimization problems where decision variables must take integer values presents unique challenges. These problems arise in various real-world applications, such as scheduling, resource allocation, and logistics, where solutions are naturally discrete. The complexity of such problems increases due to the integrality constraints, making them more difficult to solve compared to continuous optimization problems.
Common Challenges in Integer Optimization
Several challenges emerge when working with integer-based optimization problems, including:
- Non-convexity: The feasible region is often non-convex, making it difficult to apply standard solution methods that assume a smooth, continuous space.
- Combinatorial Explosion: The number of potential solutions increases exponentially as the number of variables grows, leading to longer solution times and higher computational costs.
- Difficulty in Exact Solutions: Finding exact solutions can be computationally intensive, often requiring specialized algorithms or heuristics.
Approaches to Overcome Challenges
There are various strategies for tackling these challenges in integer optimization, including:
- Branch-and-Bound: This method systematically explores feasible solutions by dividing the problem into smaller subproblems, “bounding” the regions that cannot contain the optimal solution.
- Cutting Planes: This technique iteratively refines the feasible region by adding constraints, or “cuts,” to eliminate suboptimal solutions.
- Heuristic and Metaheuristic Approaches: For large, complex problems, heuristics like genetic algorithms or simulated annealing can provide near-optimal solutions in less time.
These methods offer ways to manage the complexity and improve the efficiency of finding solutions to integer-based optimization problems, making them more tractable in practical applications.
Common Pitfalls in Optimization Models
While solving optimization problems, there are several common mistakes that can lead to incorrect or suboptimal solutions. These errors often arise from misinterpreting constraints, neglecting important factors, or using inappropriate methods. Being aware of these pitfalls is crucial for anyone working with optimization tasks to ensure accurate and efficient problem-solving.
Frequent Mistakes in Formulating Problems
One of the main sources of issues in optimization is the improper formulation of the problem. Here are some common mistakes to watch out for:
- Incorrectly Defined Constraints: Sometimes, constraints are misunderstood or oversimplified, leading to infeasible or unrealistic solutions.
- Overlooking Variable Boundaries: Failing to properly set the limits for decision variables can result in unbounded solutions or values outside the practical range.
- Misinterpreting Objective Functions: A misalignment between the problem’s goal and the objective function can cause the model to optimize the wrong aspect of the problem.
Challenges in Solving Optimization Problems
Even once the problem is well-defined, several challenges can hinder finding the optimal solution. These include:
- Convergence Issues: Some optimization algorithms may struggle to converge to an optimal solution, especially when the problem is complex or poorly scaled.
- Computational Complexity: As the problem size increases, the time and resources needed to find a solution can grow exponentially, making the task impractical without advanced techniques.
- Inadequate Tools: Using the wrong algorithm or software for the given problem type can lead to inefficiency or failure to find the correct solution.
Acknowledging and addressing these pitfalls is essential for optimizing results and ensuring that the chosen methods are suitable for the problem at hand.
Interpreting Results of Optimization Models
After solving an optimization problem, it’s essential to understand the results to ensure they provide meaningful insights. The solutions obtained from such models need to be interpreted in the context of the original problem, considering the objectives, constraints, and practical implications. Misinterpretation can lead to flawed decisions or inefficient strategies, so careful analysis is critical.
Understanding the Optimal Solution
The optimal solution represents the best outcome based on the objective function, given all the constraints. However, interpreting this solution goes beyond simply reading the final numbers. Key elements to consider include:
- Decision Variables: These values indicate the optimal quantities or choices that should be made to achieve the best result.
- Objective Value: This reflects the value of the objective function at the optimal solution, showing how well the goals of the problem have been met.
- Feasibility: It’s important to check if the solution satisfies all the problem’s constraints. A feasible solution ensures that the results are realistic and achievable.
Analyzing Shadow Prices and Sensitivity
In many optimization models, understanding the sensitivity of the solution to changes in parameters is crucial. Shadow prices, or dual values, provide insight into how the objective function would change with a slight alteration in the constraints. Key factors to analyze include:
- Shadow Prices: These values represent the worth of an additional unit of resource or constraint. A positive shadow price indicates that increasing the resource will improve the objective, while a negative value suggests that the resource is not beneficial.
- Sensitivity Analysis: This technique helps to determine how changes in the input data (such as coefficients in the objective function or constraint boundaries) can affect the optimal solution. It aids in understanding the robustness of the solution.
By carefully interpreting the results, including understanding the sensitivity of the model, decision-makers can make informed choices that align with both the model’s output and real-world considerations.
Application of Sensitivity Analysis

Sensitivity analysis is a powerful tool used to examine how the changes in input parameters of an optimization model affect the optimal solution. By exploring the relationships between variables and constraints, this technique helps identify which factors are most influential in determining the outcome. Understanding sensitivity is essential for making informed decisions, especially when dealing with uncertainty or variability in real-world situations.
In practice, sensitivity analysis allows decision-makers to evaluate the robustness of a solution under different scenarios. It provides insights into how changes in resource availability, costs, or other parameters can impact the overall performance. This approach is particularly valuable in fields such as logistics, finance, and manufacturing, where variables often fluctuate over time.
Key Applications of Sensitivity Analysis
Some common areas where sensitivity analysis can be applied include:
- Risk Management: Sensitivity analysis helps in assessing the potential risks associated with uncertain parameters and their impact on the decision-making process.
- Resource Allocation: By analyzing how changes in available resources affect the optimal distribution, sensitivity analysis can guide better allocation strategies.
- Cost Minimization: It assists in understanding how cost fluctuations or constraints adjustments might influence the overall cost structure of a project or operation.
Example of Sensitivity Analysis in Action
To illustrate the application of sensitivity analysis, consider the following simplified example where a company aims to maximize profit by deciding how much of two products to produce. The profit model is subject to various constraints, such as production capacity and material availability. The table below shows how the optimal solution changes with different values of a key parameter, the material cost:
| Material Cost | Optimal Product A | Optimal Product B | Profit |
|---|---|---|---|
| $5 | 100 units | 200 units | $1500 |
| $7 | 90 units | 210 units | $1450 |
| $10 | 80 units | 220 units | $1400 |
In this example, as the material cost increases, the number of units produced for Product A decreases, while the number for Product B increases. The profit also decreases, showing how sensitive the model is to cost changes. This type of analysis allows businesses to anticipate how changes in external factors will affect their operations and adjust their strategies accordingly.
Advanced Techniques in Optimization
As optimization challenges grow in complexity, innovative and more sophisticated methods are required to efficiently tackle larger and more intricate problems. These advanced approaches are designed to handle higher-dimensional spaces, multiple constraints, and nonlinearities within optimization models. By adopting these methods, practitioners can achieve optimal solutions faster, even in large-scale real-world scenarios where simpler algorithms may struggle.
This section delves into several cutting-edge techniques that have revolutionized optimization problems, particularly when it comes to achieving efficiency and accuracy in solving difficult problems. These strategies offer distinct advantages depending on the problem structure and the nature of the variables involved.
Interior-Point Methods
Interior-point algorithms have become popular for their ability to handle complex and large-scale problems effectively. Unlike boundary-based methods, these techniques work by navigating through the interior of the feasible region. Some of the key advantages include:
- Enhanced scalability: Suitable for solving problems with thousands of variables and constraints.
- Faster convergence: They tend to converge to the optimal solution more quickly compared to other methods.
- Numerical stability: Less prone to issues like degeneracy, which can hinder the progress of simpler algorithms.
Decomposition Methods
Decomposition is particularly useful when dealing with large and complex optimization problems. By breaking down a large problem into smaller, more manageable subproblems, these methods reduce computational complexity. Some well-known decomposition techniques include:
- Primal-Dual Decomposition: Divides the problem into primal and dual components, solving each separately for a more efficient overall process.
- Benders Decomposition: This method is ideal for problems that involve mixed-integer variables, dividing the problem into master and subproblems.
- Column Generation: Focuses on solving a restricted version of the problem and progressively adding new variables as needed.
Cutting-Plane Methods
Cutting-plane techniques are especially useful in solving integer optimization problems. These methods iteratively add constraints to the optimization problem to eliminate infeasible solutions, progressively improving the feasible region. Key features include:
- Relaxation: Solving a simplified problem without integer constraints to obtain an initial feasible solution.
- Iterative refinement: The process continues by adding “cuts” to further narrow down the solution space.
- Convergence: The method continues to iterate until an optimal or near-optimal solution is found.
Multi-Objective Optimization
Real-world optimization problems often involve balancing multiple conflicting goals. Multi-objective optimization techniques aim to find solutions that balance these trade-offs. Common strategies include:
- Pareto Optimality: Solutions are considered optimal if no other solution can improve one objective without worsening another.
- Weighted Sum Method: This approach combines multiple objectives into one by assigning a weight to each, simplifying the optimization process.
- Evolutionary Algorithms: Techniques like genetic algorithms employ population-based search methods to find optimal trade-offs between conf
Impact of Changing Constraints
When constraints within an optimization problem are altered, the solution and its feasibility can be significantly impacted. Constraints represent the limitations and requirements that define the boundaries of acceptable solutions. As these conditions evolve, the model may need to be recalculated to reflect the new environment, which can influence the optimal solution, objective values, and resource allocation strategies.
Understanding how changes in constraints affect the outcome of a problem is crucial for decision-making, especially in dynamic systems where conditions may change over time. The ability to anticipate and evaluate these shifts allows businesses and organizations to adapt to new circumstances effectively, ensuring that they continue to achieve optimal results despite the fluctuations.
Some key effects of modifying constraints include:
- Feasibility Changes: Adjustments to constraints may render previously feasible solutions invalid, requiring a reassessment of the solution space.
- Objective Function Impact: The value of the objective function may shift, either improving or worsening, depending on the direction and nature of the changes to the constraints.
- Resource Allocation Adjustment: The redistribution of resources might be necessary to meet the new set of requirements while still maintaining optimal performance.
In certain cases, small changes to constraints may lead to minimal differences in the overall solution, while larger shifts could require a complete restructuring of the solution approach. The ability to analyze these impacts through sensitivity analysis or other advanced techniques can provide valuable insights into the robustness of a model under varying conditions.
Solving Optimization Problems with Excel
Excel offers a powerful toolset for solving optimization problems, providing an accessible and effective way to model and analyze various decision-making scenarios. Whether for business planning, resource allocation, or maximizing efficiency, Excel’s Solver function can quickly find the optimal solution based on a set of variables and constraints. This makes it an invaluable resource for users who may not have access to specialized optimization software.
To solve optimization problems using Excel, the first step is to clearly define the objective function and the constraints. Once this is done, the Solver tool can be employed to find the best possible outcome. Below are the key steps to setting up and solving these problems:
Setting Up the Problem
- Define Variables: Identify the decision variables that will be adjusted to achieve the objective.
- Set Objective Function: Create a formula that represents the goal you wish to optimize, such as profit maximization or cost minimization.
- Enter Constraints: Specify the limits or conditions that the solution must satisfy, such as resource availability or budget restrictions.
Using Solver to Find the Optimal Solution
- Activate Solver: Access the Solver tool in Excel by navigating to the “Data” tab and selecting “Solver.”
- Input Parameters: Set the objective function cell, define the variables, and input any necessary constraints into the Solver configuration.
- Run Solver: Click “Solve” and allow Excel to calculate the optimal solution based on the given inputs.
By using Excel’s Solver function, users can quickly and efficiently solve complex optimization problems, making it an ideal choice for those who need practical, real-world solutions without specialized knowledge of advanced software. It’s also a helpful tool for analyzing how changes in input parameters affect the outcome, allowing for flexible decision-making and scenario analysis.
Applications in Business and Economics
Optimization techniques are widely used in business and economics to make informed decisions, allocate resources efficiently, and maximize profits. These approaches help in identifying the best solutions for problems involving resource allocation, production planning, and financial management. By formulating objectives and constraints, organizations can find the most effective ways to achieve their goals while considering limitations such as budget, time, and capacity.
In business, the applications of optimization are vast and varied. Here are some key areas where optimization plays a crucial role:
Key Applications in Business
- Production Planning: Companies use optimization models to determine the most efficient way to schedule production, minimize costs, and maximize output given limited resources.
- Supply Chain Management: Optimization helps businesses plan inventory levels, transportation routes, and supplier relationships to minimize costs and ensure timely delivery.
- Portfolio Optimization: In finance, optimization techniques are employed to create investment portfolios that maximize returns while minimizing risk, considering factors such as market conditions and risk tolerance.
- Marketing Strategy: Firms can optimize their marketing spend, targeting strategies, and pricing policies to maximize customer reach and profitability.
Applications in Economics
- Resource Allocation: Economists use optimization models to allocate scarce resources efficiently, ensuring the maximum possible output is achieved in sectors like agriculture, energy, and manufacturing.
- Pricing Strategies: Optimization can help firms determine the best pricing strategies to maximize revenue, considering factors such as competition, demand elasticity, and production costs.
- Market Equilibrium: Economists use optimization techniques to study market dynamics and determine the equilibrium price and quantity where supply and demand meet, maximizing total welfare.
In both business and economics, optimization techniques provide a powerful way to improve efficiency, reduce waste, and achieve desired outcomes in an uncertain environment. By applying these techniques, companies and governments can make more informed, data-driven decisions that lead to long-term success and sustainability.
Linear Programming in Operations Research

In the field of operations research, mathematical optimization is a fundamental tool for solving complex decision-making problems. By focusing on improving efficiency and resource utilization, these techniques assist organizations in maximizing their objectives, such as profit or productivity, while adhering to various constraints like budget, capacity, and time. Operations research employs a variety of methods to optimize processes, making it a critical component in industries such as logistics, manufacturing, finance, and healthcare.
Applications in Operations Research
- Supply Chain Optimization: Efficient management of supply chains relies heavily on optimization methods. These models help businesses determine the most cost-effective way to source, store, and transport goods while minimizing waste and meeting demand.
- Scheduling and Workforce Planning: Operations research techniques are used to allocate tasks and schedule workers effectively, ensuring that operations run smoothly without overloading resources or missing deadlines.
- Inventory Management: Optimization is employed to maintain optimal inventory levels that minimize holding costs while preventing stockouts and meeting customer demand.
- Project Management: In large-scale projects, optimization models are used to allocate resources efficiently, manage timelines, and evaluate risks, ensuring that project goals are met on time and within budget.
Key Benefits in Operations Research

- Cost Reduction: By finding the most efficient allocation of resources, organizations can significantly cut costs, reduce waste, and maximize returns on investment.
- Improved Decision-Making: Mathematical models allow decision-makers to evaluate various scenarios and make data-driven decisions that align with organizational goals.
- Enhanced Resource Utilization: These methods ensure that available resources are used in the most productive manner, whether it’s labor, materials, or capital.
- Risk Management: Optimization models help organizations assess potential risks and create strategies to mitigate them, ensuring smooth operations in the face of uncertainty.
In summary, optimization techniques play a crucial role in operations research by providing organizations with the tools to solve complex problems and make more informed, strategic decisions. These methods are indispensable in achieving efficiency, reducing costs, and maintaining competitive advantage in a rapidly evolving business environment.
Solving Multiple Linear Optimization Problems
When working with several optimization tasks simultaneously, the challenge is to ensure that all objectives are met while adhering to various constraints. This often arises in situations where multiple processes need to be optimized at the same time, such as in production planning, supply chain management, or resource allocation. Each problem might have its own unique set of requirements, but the goal is to find solutions that work together without violating the constraints of any individual task.
Solving multiple related problems requires careful analysis and sometimes the use of specialized techniques that handle the interdependencies between them. The key is to structure the problems in such a way that each solution contributes to the overall optimal outcome, whether that’s maximizing profits, minimizing costs, or balancing multiple conflicting objectives.
Approach to Solving Multiple Problems
Here’s a systematic approach to addressing multiple related optimization problems:
- Identify the objectives and constraints for each problem.
- Formulate the problems into mathematical models, ensuring that each model is solvable independently.
- Analyze how the models interact and adjust for shared resources or constraints.
- Apply optimization methods such as the simplex method, branch and bound, or others to find the best solution that satisfies all conditions.
Example: Solving Multiple Production Optimization Tasks
Suppose a company needs to optimize the production of two products. Each product has different constraints, but the company wants to maximize total profit while using shared resources like labor and raw materials. The problem can be broken down into separate models for each product, as shown below:
Product Objective Function (Profit) Constraints Product A Maximize profit = 30x + 40y 2x + y ≤ 50, x ≥ 0, y ≥ 0 Product B Maximize profit = 25x + 50y x + 3y ≤ 60, x ≥ 0, y ≥ 0 By solving the two models together, the company can determine the optimal production amounts for both products to maximize total profit while respecting shared constraints such as labor and material usage.
In such scenarios, it is essential to consider the interdependencies between the problems. Adjustments in one problem may affect the available resources or constraints of another, which is why a coordinated approach is necessary to achieve the best overall outcome.
Tips for Passing Optimization Assessments
Achieving success in optimization-related assessments requires a blend of solid understanding, methodical practice, and efficient time management. Being prepared for complex problem-solving scenarios and mastering key techniques can help you excel, even when faced with challenging tasks. The following tips will guide you through effective preparation and strategies to perform your best during the test.
Master Key Concepts and Methods
Building a strong foundation in the core principles of optimization is essential. Understanding the fundamental techniques and how to apply them will increase your chances of success. Focus on:
- Understanding different problem types, such as maximization and minimization problems.
- Familiarizing yourself with solution methods like graphical methods, the simplex approach, and duality.
- Knowing how to interpret and manage constraints, ensuring you can define feasible regions and objectives correctly.
Practice Regularly and Simulate Test Conditions
Practice is crucial for mastering optimization methods. The more problems you solve, the more confident you will become in your ability to apply the right techniques under time pressure. To practice effectively:
- Work through various types of problems to become comfortable with diverse scenarios.
- Time yourself when solving practice exercises to simulate the actual test environment.
- Review your work after solving problems, learn from mistakes, and refine your approach.
Here’s a practical approach to preparing for assessments:
Step Action 1 Read and understand the problem thoroughly. 2 Identify the objective and constraints clearly. 3 Formulate the problem into mathematical terms. 4 Choose and apply the appropriate solution technique. 5 Verify your solution and check for optimality. By following these steps, you can streamline your problem-solving process, ensuring that you approach each question with a clear, methodical strategy. This will help you stay organized and improve your performance on the assessment.