
Mastering complex mathematical concepts requires more than just understanding the theory; it demands active problem-solving and critical thinking. For those aiming to excel in higher-level assessments, practicing with real-world examples and challenges is essential. This section will guide you through strategies to enhance your performance and boost your confidence in tackling difficult tasks.
Achieving success in mathematics depends on your ability to break down problems, apply the correct methods, and interpret your results accurately. Knowing how to approach each question methodically can make all the difference when it comes to time management and accuracy.
Effective preparation involves engaging with a variety of scenarios that test your understanding from multiple angles. Through consistent practice, you’ll build the skills necessary to navigate even the most intricate questions. The following sections provide detailed insights into optimizing your approach and avoiding common pitfalls along the way.
AP Calculus AB Exam 2025 Overview
The upcoming assessment is designed to evaluate a student’s ability to apply mathematical concepts to solve complex problems. The focus is on understanding key principles and demonstrating the capacity to work through challenges that test both conceptual and procedural knowledge. It is important to approach this task with a clear strategy to ensure success under timed conditions.
Structure of the Assessment
This evaluation is divided into two main sections, each targeting different aspects of the subject. The first section generally emphasizes multiple-choice questions, where quick reasoning and problem-solving skills are required. The second part tests a deeper understanding, demanding students to provide detailed solutions that showcase their methodical approach to problem-solving. It is critical to develop a strong grasp of both theoretical and practical aspects to excel in this format.
Key Areas of Focus

Students will need to demonstrate proficiency in several key areas, including limits, derivatives, integrals, and their applications. Each concept is tested in various contexts, requiring not only the ability to compute solutions but also to explain reasoning and interpret results. A solid understanding of these topics will be essential for success, as they form the foundation for the more complex problems encountered in the assessment.
Importance of Free Response Questions
In any high-level assessment, the ability to explain and justify your thought process is just as important as obtaining the correct result. Tasks that require detailed solutions are a critical part of the evaluation, as they give a clear picture of a student’s comprehension and problem-solving ability. These types of questions test a student’s capacity to organize their thoughts, apply appropriate methods, and communicate their reasoning effectively.
Why These Tasks Matter

Unlike multiple-choice questions, which only assess recognition and quick recall, these tasks offer a deeper challenge. They push students to demonstrate their full understanding of concepts and their ability to apply those concepts in varied situations. The key lies not just in getting the right answer, but in clearly articulating the steps taken to reach it.
Key Benefits of Detailed Solutions
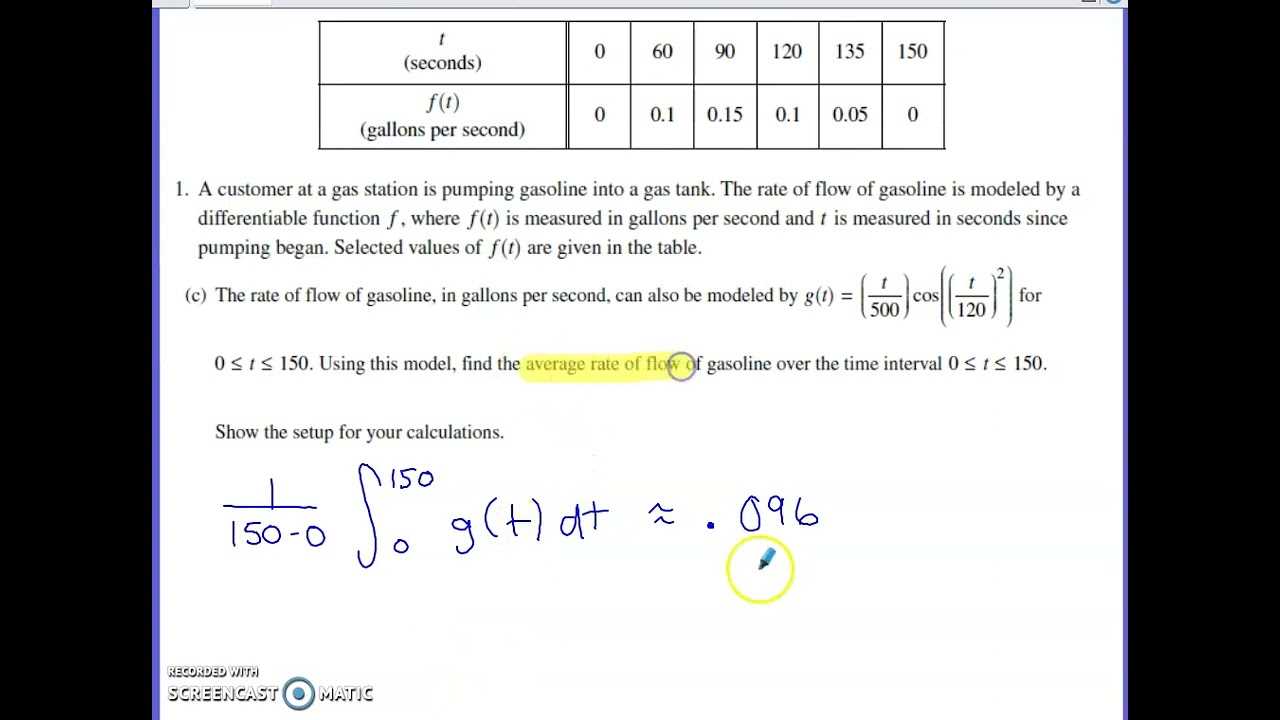
By engaging with problems that require comprehensive answers, students develop a more thorough understanding of the material. These types of tasks also allow students to show their reasoning, which can make a significant difference in scoring. Teachers and graders value clear, structured responses that demonstrate mastery of concepts and methods. Below is a summary of key skills tested through detailed problem-solving:
| Skill Tested | Description |
|---|---|
| Conceptual Understanding | Demonstrates comprehension of core principles and their real-world applications. |
| Problem-Solving Process | Requires a structured approach to solving complex problems step by step. |
| Mathematical Communication | Tests the ability to explain reasoning and support solutions with appropriate methods. |
How to Approach Free Response Problems
Tackling complex mathematical tasks requires a clear strategy and organized thinking. When faced with detailed problem-solving challenges, it is crucial to break down each question into manageable parts. The process involves not only solving the problem but also clearly explaining the steps taken to arrive at the solution. This approach ensures that you demonstrate your understanding of the subject matter while maintaining clarity and precision in your reasoning.
Step-by-Step Problem Solving
To approach detailed tasks effectively, follow a methodical process. The key steps include:
- Understand the Problem: Read the question carefully and identify what is being asked. Pay attention to any conditions or constraints provided in the problem.
- Identify Key Concepts: Determine which principles or formulas apply to the situation. Consider any relevant theories or methods you have learned.
- Plan Your Approach: Outline the steps you will take to solve the problem. Break the process down into smaller, more manageable tasks.
- Execute the Solution: Perform the necessary calculations or apply the correct methods. Be thorough in your work, ensuring each step is accurate.
- Explain Your Work: Clearly write out each step of your solution process. Make sure to explain how you arrived at your conclusion.
- Review Your Solution: After solving, double-check your work to ensure accuracy and clarity. Confirm that your answer is complete and matches the question’s requirements.
Tips for Success
Here are some additional tips to help you succeed in solving detailed problems:
- Stay Organized: Keep your work neat and structured to avoid confusion.
- Work Methodically: Focus on one step at a time, ensuring that each part of your solution is correct before moving on.
- Use Appropriate Notation: Be consistent in your use of mathematical symbols and units. This ensures your solution is easily understood.
- Show All Work: Even if you can solve a problem mentally, always write down each step. It demonstrates your process and allows for partial credit if needed.
Key Concepts Tested in AP Calculus

In any advanced mathematical assessment, students are expected to demonstrate a strong understanding of fundamental principles and their real-world applications. The key concepts tested often involve critical ideas that serve as the building blocks for more complex problem-solving tasks. Mastery of these concepts is essential, as they are frequently revisited throughout the test in various contexts, requiring both theoretical knowledge and practical application.
Among the core areas typically assessed are concepts related to rates of change, accumulation, and the relationships between functions and their derivatives. Additionally, integrals and their various uses are heavily tested, particularly in terms of calculating areas and solving problems involving accumulation. These foundational topics not only serve as the foundation for higher-level mathematical studies but are also crucial for solving a wide range of real-world problems.
Having a thorough understanding of these core ideas is essential for success, as they form the basis for interpreting and solving the more intricate challenges presented in the evaluation. Being able to connect these principles across different problem types is a key skill that will enable you to approach complex questions with confidence.
Effective Study Tips for Success
Success in advanced mathematical assessments relies heavily on focused preparation and strategic study techniques. A well-planned study routine allows students to deepen their understanding and improve their problem-solving abilities. Effective preparation not only involves reviewing key concepts but also practicing how to apply those principles in various contexts.
Active Learning Techniques
One of the most effective ways to retain information is through active learning. Instead of passively reading through notes or textbooks, engage with the material by solving problems, explaining concepts out loud, or teaching the material to someone else. This reinforces your understanding and helps identify areas that need further attention. Additionally, actively working through problems allows you to apply the concepts in a hands-on way, which is crucial for long-term retention.
Time Management and Practice
Time management is key to ensuring consistent progress. Set aside dedicated time each day for focused study, breaking up sessions into manageable chunks. Avoid cramming the night before by spreading your study time out over weeks or months. Practice regularly with a variety of problem types to ensure you are prepared for any situation. The more problems you solve, the more comfortable and confident you’ll become in applying your knowledge.
Breaking Down the Free Response Format
In any comprehensive mathematical assessment, tasks requiring detailed explanations are designed to evaluate a deeper level of understanding. These questions test not only your ability to solve problems but also your capacity to organize and articulate your thought process clearly. The format of such tasks typically involves multiple components that require careful attention to detail and methodical problem-solving.
Understanding the Structure
Questions that require written solutions are usually broken down into distinct parts, each testing a different skill or concept. Below is a breakdown of the common elements you may encounter in this type of task:
- Part 1: Initial Problem Setup – In this section, you’ll be asked to identify key information and formulate a strategy for solving the problem.
- Part 2: Mathematical Calculation – This is where you apply the appropriate methods to compute a solution, often requiring multiple steps.
- Part 3: Justification – After finding a solution, you will be expected to explain the reasoning behind each step and the method you used.
- Part 4: Interpretation – This section might ask you to interpret the result in the context of the problem or real-world scenario.
Tips for Success in Structured Tasks
To excel in these types of questions, consider the following strategies:
- Plan Your Approach: Before diving into calculations, carefully read the problem and break it down into smaller, more manageable tasks.
- Show Your Work: Always write out each step in your solution. Clear, logical progression is key for demonstrating your understanding.
- Double-Check Your Results: Ensure that your answer makes sense in the context of the question and verify your calculations for accuracy.
- Focus on Clarity: Your explanation should be as clear as the solution itself. A well-structured response is easier to follow and earns more credit.
Understanding Grading Criteria for Responses
When tackling detailed problem-solving tasks, understanding how your work will be evaluated is essential. The grading process is designed to assess not only the final solution but also the clarity, structure, and accuracy of your explanation. Each part of your answer, from the initial setup to the final interpretation, is scrutinized to ensure that you demonstrate a complete understanding of the concepts involved.
Key Factors in the Grading Process
The following factors are typically considered when grading written solutions:
- Correctness: The most important factor is whether the final solution is accurate. A correct answer demonstrates that you applied the right methods and formulas.
- Logical Progression: Your response should follow a clear, logical sequence. Each step should be connected and easy to follow, showing how you arrived at the solution.
- Clarity of Explanation: Simply solving the problem is not enough; you must also explain your reasoning clearly. Graders look for well-organized, coherent explanations that demonstrate your thought process.
- Use of Proper Notation: Using correct mathematical symbols and notation ensures that your solution is professional and precise. This includes clearly labeling variables and using appropriate terminology.
- Completeness: Be sure to address all aspects of the question. Incomplete answers, even if correct, may lose points for missing steps or failing to fully address the problem.
How to Maximize Your Score
To maximize your score, focus on the following strategies:
- Show Your Work: Always write out each step in your solution. This demonstrates your understanding and ensures partial credit if the final answer is incorrect.
- Provide Clear Explanations: Clearly articulate the reasoning behind each step. A grader should be able to follow your thought process easily.
- Review for Accuracy: Before submitting your solution, double-check your calculations and explanations for errors. Make sure your work is neat and well-organized.
- Practice Problem-Solving: Regular practice will help you become more efficient at solving problems and presenting your answers in a clear, concise manner.
Common Mistakes to Avoid in Calculus
When solving complex mathematical problems, it’s easy to make mistakes, especially when the tasks involve multiple steps or abstract concepts. Understanding common pitfalls can help you avoid errors that may cost you valuable points. Many mistakes stem from misinterpreting the problem, skipping essential steps, or applying incorrect methods. By recognizing these errors, you can improve your problem-solving skills and approach each question with greater confidence.
Common Errors in Problem-Solving
Here are some of the most frequent mistakes that students make when tackling challenging mathematical tasks:
- Skipping Steps: Failing to show all intermediate steps can lead to confusion and mistakes. Even if you’re confident in the final answer, skipping steps can obscure the logic behind your solution.
- Misinterpreting the Question: Sometimes, students misread the problem or overlook key information. Always read the problem carefully, ensuring that you understand what is being asked before proceeding.
- Incorrect Application of Formulas: Applying the wrong formula or using it incorrectly is a common mistake. Make sure you fully understand which formula is relevant to the specific task at hand.
- Ignoring Units or Context: For problems involving real-world applications, failing to consider units or the context of the question can lead to incorrect conclusions or answers.
- Overlooking Negative Signs: In complex calculations, forgetting to account for negative signs can lead to incorrect results. Double-checking your work can help catch this simple but impactful mistake.
How to Avoid These Mistakes
To reduce the likelihood of making these errors, try the following strategies:
- Double-Check Your Work: Before finalizing your answer, go over your steps to ensure that no part of the solution is missing or incorrect.
- Stay Organized: Keep your work neat and orderly, so it’s easier to identify mistakes and follow your logic.
- Practice Regularly: The more problems you solve, the more familiar you’ll become with common pitfalls. Practice will help you avoid these errors and improve your overall performance.
- Understand the Concepts: Don’t just memorize formulas–understand the underlying concepts. This will help you apply the correct methods more effectively.
Strategies for Time Management During the Exam
Effective time management is crucial when tackling complex problem-solving tasks under pressure. With limited time to answer each question, it’s essential to allocate your time wisely to maximize your performance. Strategic planning before and during the assessment can help ensure that you complete each section thoughtfully and efficiently, without rushing through critical steps or leaving questions unfinished.
Start by familiarizing yourself with the total time available and dividing it proportionally across the sections based on their difficulty and point value. During the test, it’s important to keep track of time and adjust your pace as necessary, ensuring that you leave enough time to review your work at the end.
Effective Strategies to Stay on Track
Here are several tips to help you manage your time efficiently during the assessment:
- Plan Ahead: Before you start, quickly skim through all the questions to get a sense of their difficulty and length. This allows you to prioritize your time and identify any problems that may require more effort.
- Set Time Limits: For each question, set a rough time limit based on its complexity. If you’re spending too much time on one question, move on and come back to it later if necessary.
- Start with What You Know: Begin with the questions you find easiest. This will boost your confidence and ensure that you earn points quickly, leaving more time for the more challenging tasks.
- Avoid Perfectionism: Focus on completing the tasks rather than striving for flawless solutions. If you’re unsure about a problem, jot down your thoughts and move forward. You can return to refine your answer if time permits.
How to Stay Calm and Focused
Maintaining composure is key to managing time effectively. Here’s how to stay calm and focused throughout:
- Practice Under Time Pressure: Before the actual assessment, simulate timed conditions during your study sessions. This will help you become accustomed to managing time while solving complex problems.
- Take Short Breaks: If you’re feeling overwhelmed, take brief moments to clear your mind. A short break can help you refocus and prevent burnout during the assessment.
- Keep Track of Time: Use a watch or a clock to monitor your progress. Keep an eye on how much time you have left for each section to avoid spending too long on any single question.
Resources for Practicing Free Response Questions
To excel in assessments that require complex problem-solving, it’s essential to practice regularly using high-quality resources. There are various tools available that can help you develop a deeper understanding of the material and improve your ability to respond to challenging questions. From textbooks to online platforms, the right resources can guide you in honing the skills necessary for success.
Utilizing a variety of resources helps diversify your learning experience, providing access to different types of problems and solutions. This approach ensures that you are well-prepared for any task, as you’ll become familiar with a range of concepts and techniques that may appear in the assessment.
Top Resources for Preparation

Here are some excellent resources to consider for focused practice:
- Official Practice Materials: Many organizations and institutions provide official materials, including past assessments and sample problems. These resources are a great way to familiarize yourself with the format and the level of difficulty.
- Online Learning Platforms: Websites like Khan Academy, Coursera, or edX offer free and paid courses that cover various topics. These platforms often include practice problems and interactive tools that allow you to track your progress.
- Textbooks and Study Guides: Comprehensive textbooks dedicated to mathematical concepts typically feature numerous practice problems with detailed solutions. Additionally, specialized study guides can provide targeted exercises and tips to improve problem-solving skills.
- Mobile Apps: Many apps offer practice problems, quizzes, and step-by-step solutions. These apps allow you to study on the go, making it easy to practice anytime and anywhere.
- Peer Study Groups: Collaborating with peers can offer valuable insights and different approaches to solving problems. Study groups provide a supportive environment where you can exchange ideas and solve challenges together.
How to Make the Most of These Resources
To maximize the effectiveness of your study sessions, follow these tips when using the above resources:
- Practice Regularly: Consistency is key. Set aside dedicated time each week to focus on solving problems. The more you practice, the more confident you’ll become in tackling similar tasks.
- Review Solutions Thoroughly: Don’t just focus on the answers. Take the time to review the steps involved in solving each problem. Understanding the process is as important as getting the correct result.
- Simulate Real Conditions: Try to replicate the conditions of the actual task by timing yourself while completing problems. This will help improve your time management and reduce stress during the real test.
AP Scoring Guide Explained
The scoring process for assessments that involve complex problem-solving follows a detailed and structured approach, ensuring that every aspect of a student’s work is evaluated fairly. Understanding the criteria used to grade these tasks is essential for students aiming to maximize their performance. The guide provides a breakdown of how scores are assigned based on the quality of responses, the application of relevant techniques, and the logical clarity of the solutions presented.
The scoring system is typically divided into different components, each corresponding to specific aspects of the response. From initial setup to the final solution, each part of the task is assessed to determine how well the student demonstrates their understanding of the material. Recognizing how each component contributes to the total score can help students focus on areas that require more attention.
Components of the Scoring Process
Here are the key elements that are considered when grading the assessment:
- Correct Setup: The initial steps in solving the problem, including identifying the appropriate approach and applying relevant concepts, are crucial. If the setup is incorrect, even a correct final answer may not earn full points.
- Mathematical Accuracy: The accuracy of the calculations, including any intermediate steps, is a major factor in scoring. Mistakes in arithmetic or algebra can lead to a loss of points.
- Logical Reasoning: Clear and coherent explanations of how the solution was derived are vital. Responses that show reasoning behind each step are more likely to earn higher marks than those that simply present the answer.
- Final Answer: While not always the most important factor, providing the correct answer still plays a significant role in determining the score. However, a correct answer without adequate reasoning may not always receive full credit.
- Completeness: Ensuring that every part of the question is addressed is essential for maximizing the score. Partial answers or missing steps can result in deductions.
How to Maximize Your Score
To achieve the best possible score, focus on these strategies:
- Show All Work: Clearly outline each step in your solution. Even if you can solve the problem mentally, writing down all the intermediate steps ensures that you earn credit for your approach.
- Be Methodical: Follow a logical progression from start to finish. Avoid jumping directly to the final answer without explaining how you arrived there.
- Review and Double-Check: Take time to review your work before submitting. Look for any potential errors in logic or calculation that may have been missed during the first pass.
Using Past Assessments to Prepare Effectively
Reviewing previous assessments is one of the most effective strategies for achieving success in any rigorous test. By studying past materials, students gain insight into the types of questions typically asked, the level of difficulty, and the expected structure of the tasks. This not only helps in becoming familiar with the format but also allows students to identify patterns in problem-solving techniques and areas that require more focus.
One of the key benefits of working through past assessments is the opportunity to simulate real test conditions. Time constraints, the sequence of questions, and the format can all be practiced in advance. This prepares students for the pressure of timed assessments and enhances their ability to manage their time efficiently during the actual test.
How Past Materials Enhance Preparation
Here’s how reviewing past assessments can improve your study strategy:
- Familiarity with Question Types: Repeated exposure to similar problem types helps students anticipate what to expect and reduces anxiety on test day.
- Identifying Weaknesses: Working through past tasks allows you to pinpoint areas where you need additional practice. By revisiting these areas, you can strengthen your understanding and improve your performance.
- Time Management Practice: Simulating test conditions by timing yourself helps to improve speed and efficiency, ensuring you can complete tasks within the given time frame.
- Building Confidence: Successfully completing past questions boosts confidence and provides a sense of accomplishment, making you more prepared for the real assessment.
Maximizing the Value of Past Materials
To make the most of past materials, here are some tips:
- Work Under Test Conditions: Set a timer and complete questions as if you were in the real assessment environment. This helps you get used to the pressure and improves your time management skills.
- Analyze Mistakes: After completing the questions, thoroughly review your mistakes. Understanding why you got something wrong will deepen your comprehension and prevent similar errors in the future.
- Focus on Feedback: If past materials include solutions or scoring guides, use them to understand what graders look for in high-quality responses. This can guide you in refining your approach.
What to Expect on the 2025 Assessment
Preparing for a rigorous academic assessment requires an understanding of what to expect during the actual test. Each assessment follows a structured format designed to evaluate a wide range of skills. By becoming familiar with the structure and content of the tasks, students can approach the test with confidence and focus on demonstrating their knowledge effectively.
The upcoming assessment will focus on core principles that test both conceptual understanding and problem-solving abilities. Expect a variety of tasks that challenge your analytical thinking, including both multiple-choice questions and open-ended tasks. The ability to apply theoretical knowledge in practical situations will be key to success.
Task Structure and Question Types
Here’s a breakdown of what to anticipate when tackling each section:
- Conceptual Understanding: You will encounter questions that assess your grasp of core ideas. These may involve theoretical explanations, definitions, or the application of formulas.
- Problem-Solving: Expect to solve complex problems that require you to apply different mathematical techniques. You will need to demonstrate logical reasoning and clearly show your work.
- Time Management: Since there will be a time limit, it is important to allocate sufficient time to each section and not linger too long on any one question. Effective pacing is essential for completing the test on time.
- Graphical Interpretation: Be prepared to analyze graphs and diagrams, as visual representations often play a critical role in problem-solving tasks.
Key Areas of Focus
While specific tasks may vary, the following key areas will likely be emphasized:
- Understanding Functions: The assessment will test your knowledge of various types of functions, including their properties and applications in solving real-world problems.
- Analyzing Rates of Change: Expect tasks that involve determining how one quantity changes in relation to another, a skill essential for many applied mathematical concepts.
- Integration Techniques: Be prepared to solve problems that involve calculating areas, volumes, and other quantities related to integration.
Reviewing Key Theorems for the Assessment
Understanding and applying key theorems is essential for success in any advanced mathematical assessment. These fundamental principles form the backbone of many problems, and knowing them well will allow you to approach various tasks with confidence. Review the most important theorems to ensure that you can apply them effectively under test conditions.
Throughout your preparation, focus on the core concepts that are frequently tested. Being able to recall these theorems, understand their conditions, and apply them to solve problems is a valuable skill. Below are some of the most important theorems that you should review before the assessment:
| Theorem | Key Idea | Application |
|---|---|---|
| Fundamental Theorem of Calculus | Links the concept of the derivative of a function to its integral. | Used to evaluate integrals, particularly when the limits of integration are provided. |
| Mean Value Theorem | Guarantees that at least one point on a continuous curve has a tangent equal to the average slope between two points. | Helpful in proving results involving rates of change, especially for optimization problems. |
| Integration by Parts | Provides a method for integrating the product of two functions. | Useful in evaluating integrals of products or when one function can be easily differentiated while the other can be easily integrated. |
| Fundamental Theorem of Algebra | States that every non-constant polynomial equation has at least one complex root. | Important for solving polynomial equations and understanding their roots. |
By understanding and practicing the application of these theorems, you will enhance your ability to approach different types of problems that are likely to appear in the assessment. It’s crucial to not just memorize these theorems, but to understand how to apply them effectively to solve problems and answer questions during the assessment.
How to Master Graphing in Advanced Mathematics
Mastering graphing is an essential skill in advanced mathematics. Being able to visualize functions and their behaviors provides a deeper understanding of the underlying concepts and helps solve complex problems. Whether you’re analyzing the slope of a curve, finding points of intersection, or understanding the behavior of a function as it approaches infinity, graphing is a tool that makes abstract ideas more tangible.
To master graphing, it’s important to develop a systematic approach and understand the key features of a graph. Below are steps and strategies that will help you improve your graphing skills:
- Understand Key Concepts: Familiarize yourself with concepts such as limits, derivatives, and integrals. Knowing how these concepts translate into the shape of a graph will help you identify important features like local maxima, minima, and asymptotes.
- Sketch Basic Graphs First: Before diving into more complicated functions, practice sketching the graphs of simple functions, such as linear, quadratic, and exponential functions. This helps you recognize common patterns.
- Identify Critical Points: Critical points, such as intercepts, maxima, minima, and points of inflection, are crucial when graphing. Being able to calculate these points quickly will allow you to sketch more accurate graphs.
- Analyze End Behavior: Study the behavior of a function as it approaches infinity or negative infinity. Understanding the asymptotic behavior of a function is key to sketching its overall shape.
- Practice with Transformations: Learn how basic transformations–like shifts, stretches, and reflections–affect the graph of a function. This skill will make it easier to graph more complex functions by transforming simpler graphs.
By following these steps and consistently practicing, you’ll not only become more efficient at graphing but also gain a deeper understanding of the behavior of different types of functions. Graphing isn’t just about drawing curves–it’s about interpreting and understanding the mathematical relationships that shape them.
Building Confidence for Test Day
Confidence is one of the most important factors that can determine your performance on test day. It’s not just about knowing the material, but also about believing in your ability to apply that knowledge under pressure. Preparing mentally is just as crucial as mastering the content itself. With the right mindset and effective preparation, you can face the challenge with calm assurance and perform at your best.
Strategies to Build Confidence
Here are some strategies to help boost your self-assurance and set you up for success:
- Consistent Practice: Regularly solving problems, especially those from past assessments, will help you become familiar with the format and types of questions you may encounter. The more problems you tackle, the more confident you’ll feel when approaching unfamiliar ones.
- Focus on Weak Areas: Identify the areas where you struggle the most and dedicate extra time to improving them. Knowing your weaknesses and working to strengthen them will increase your overall confidence.
- Simulate Test Conditions: Practice under timed conditions to get used to the pressure of working within a set time limit. This can help reduce anxiety and improve your time management on the actual day.
- Positive Visualization: Visualize yourself succeeding. Picture yourself approaching the test with calm focus, answering questions with ease, and finishing the test confidently.
Maintaining a Positive Mindset
A positive attitude is essential for overcoming nerves and maintaining clarity during the assessment. Here are some tips to maintain a positive mindset:
- Stay Calm and Relaxed: Practice relaxation techniques such as deep breathing or meditation before the test to calm your mind and reduce stress.
- Believe in Your Preparation: Trust in the effort you’ve put in. Remember, every bit of preparation counts toward your success.
- Stay Present: Focus on one problem at a time and avoid worrying about what comes next. Tackling each question with full attention will help prevent feelings of being overwhelmed.
| Strategy | Benefit |
|---|---|
| Consistent Practice | Familiarizes you with test structure and question types, increasing comfort on test day. |
| Focus on Weak Areas | Improves skills where you are most vulnerable, boosting confidence in all topics. |
| Simulate Test Conditions | Prepares you for the time pressure, reducing anxiety on test day. |
| Positive Visualization | Mentally primes you for success, creating a sense of readiness and calm. |
By incorporating these strategies into your preparation, you’ll not only improve your knowledge but also your confidence, giving you the edge you need to perform at your best when the time comes.