
When preparing for a major assessment, it’s essential to thoroughly review and reinforce the core principles of mathematics. A solid grasp of fundamental skills will not only boost your confidence but also increase your ability to solve complex problems efficiently. In this guide, we will explore critical topics that will help you sharpen your problem-solving abilities and improve your understanding of key mathematical concepts.
Building a strong foundation is crucial for tackling more challenging questions. By focusing on foundational techniques and understanding the logic behind various mathematical operations, you’ll be better prepared for the final evaluation. This section offers step-by-step insights, explanations, and approaches designed to clarify difficult topics and ensure that you’re ready for any question that might arise.
Throughout this guide, you will find various examples and problem-solving strategies. Whether you’re working through equations or interpreting graphs, each example will guide you toward mastering essential skills. The goal is to not only improve your test scores but also to develop a deeper understanding of the subject that will benefit you in future mathematical studies.
Algebra 1 End of Course Practice Answers
Successfully completing a mathematical assessment requires more than just memorizing formulas. It involves understanding the relationships between concepts, recognizing patterns, and applying techniques to solve problems. This section provides the necessary tools to review key concepts effectively and practice various types of exercises that will help solidify your knowledge and improve performance on the final test.
Key Techniques to Review
Focus on mastering fundamental problem-solving methods. Whether it’s simplifying expressions, solving for unknowns, or interpreting functions, consistent practice will ensure you are comfortable with different types of questions. Work through each type of problem step-by-step, understanding the underlying principles that make these techniques effective.
Practical Examples and Solutions
Reviewing examples is an essential part of mastering mathematical concepts. In this section, you’ll find worked-out solutions to common problems that will guide you through the process. Each example is designed to highlight crucial steps, helping you understand how to approach similar questions in your own assessment.
Key Concepts to Master for Algebra 1
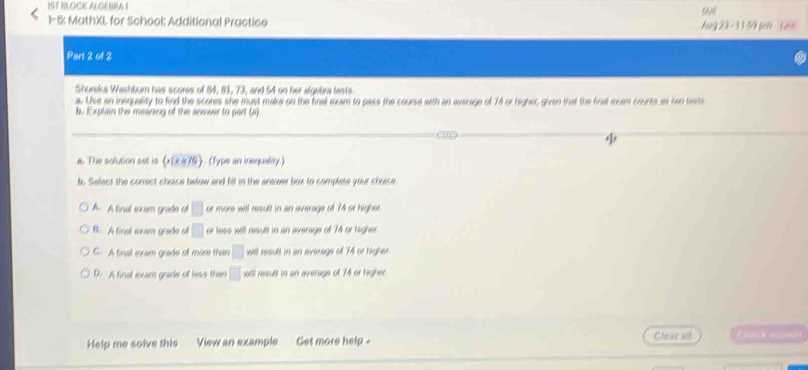
To excel in any mathematical assessment, it is essential to focus on understanding core principles that will form the foundation of more complex problem-solving techniques. Mastering these concepts will not only prepare you for success in exams but also help build the skills necessary for more advanced studies. By familiarizing yourself with the various topics and their applications, you’ll be ready to tackle a wide range of questions with confidence.
The following table outlines some of the most important areas to concentrate on, along with their key components. These concepts are crucial for solving a variety of problems and should be reviewed thoroughly to ensure a strong understanding:
| Concept | Description |
|---|---|
| Equations and Inequalities | Understanding how to manipulate and solve both linear and nonlinear equations and inequalities is fundamental for progressing in mathematics. |
| Functions and Graphs | Being able to interpret and graph various types of functions is key to understanding the relationships between variables. |
| Exponents and Powers | Familiarizing yourself with exponent rules and how they apply to expressions will allow you to simplify and solve more efficiently. |
| Factoring | Breaking down complex expressions into simpler factors is an essential skill for solving polynomial equations. |
| Rational Expressions | Mastering how to work with fractions that involve variables is necessary for solving a wide range of algebraic problems. |
Solving Linear Equations and Inequalities
Solving equations and inequalities is a fundamental skill in mathematics that allows you to find unknown values. Whether you are dealing with simple or complex expressions, understanding the methods for solving these problems is essential for progressing in mathematical studies. These techniques provide a structured approach to solving for variables and determining the range of possible solutions, especially when working with real-world scenarios.
Linear equations involve expressions where the variable is raised to the first power, and solving them typically involves isolating the variable on one side of the equation. Inequalities, on the other hand, deal with relationships between expressions and require special attention when it comes to graphing the solution set. Both concepts share similar solving steps but differ when interpreting the results, particularly with respect to directionality and the use of inequality symbols.
Mastering these techniques is crucial, as they serve as the foundation for more complex algebraic operations and are commonly tested in assessments. By practicing the methods outlined for solving linear equations and inequalities, you can build confidence and improve your problem-solving abilities in various mathematical contexts.
Understanding Polynomials and Their Operations
Polynomials are mathematical expressions that involve sums or differences of terms, each with a variable raised to a power. Understanding how to work with these expressions is essential for solving a variety of problems. Polynomials play a significant role in many areas of mathematics and are often encountered in equations that describe real-world relationships. By mastering operations involving polynomials, you will be able to simplify complex expressions and solve more intricate problems effectively.
Key Concepts in Polynomials
Before diving into operations, it’s important to grasp the basic components of a polynomial. A typical polynomial consists of terms that include a variable, a coefficient, and an exponent. These terms are combined using addition, subtraction, or multiplication. The degree of the polynomial is determined by the highest exponent in the expression.
- Terms: Components of a polynomial, consisting of a coefficient and a variable raised to a power.
- Degree: The highest exponent of the variable in the polynomial.
- Coefficients: The numerical factor in front of the variable in each term.
Operations with Polynomials
There are several key operations that you will frequently encounter when working with polynomials. These operations include addition, subtraction, multiplication, and division. Understanding how to execute these steps properly will help you manipulate polynomials and simplify expressions efficiently.
- Adding and Subtracting: Combine like terms by adding or subtracting the coefficients of terms with the same exponent.
- Multiplying: Use the distributive property (also known as the FOIL method for binomials) to multiply terms in a polynomial.
- Dividing: Polynomial division can be done using long division or synthetic division techniques, depending on the complexity of the expression.
Mastering these operations will provide a strong foundation for solving more complex equations and performing higher-level tasks in mathematics.
Graphing Functions and Their Properties
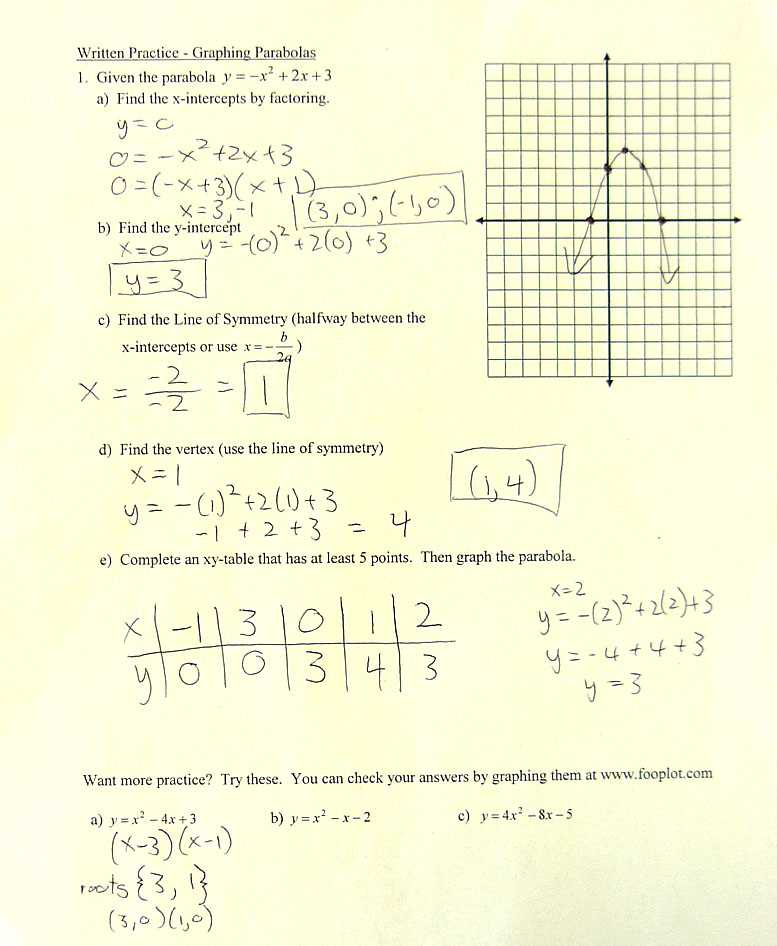
Graphing functions involves plotting data points on a coordinate plane to visually represent the relationship between variables. Understanding the behavior of these graphs allows you to interpret mathematical relationships more effectively and predict outcomes. Whether you’re analyzing linear relationships or more complex curves, knowing how to graph functions is essential for solving problems in mathematics and applied fields.
The properties of a function, such as its domain, range, intercepts, and symmetry, can provide valuable insights into how the function behaves. Analyzing these features helps in understanding the graph’s shape and how it responds to different values of the input variable.
| Property | Description |
|---|---|
| Domain | The set of all possible input values (x-values) that the function can accept. |
| Range | The set of all possible output values (y-values) that the function can produce. |
| Intercepts | The points where the graph crosses the axes. These include the x-intercept (where y = 0) and the y-intercept (where x = 0). |
| Symmetry | Some functions have symmetry, meaning the graph is identical on both sides of a line (vertical, horizontal, or rotational symmetry). |
| Asymptotes | Lines that the graph approaches but never touches or crosses. They represent limits that the function reaches as x approaches infinity or a particular value. |
By understanding these properties, you can more easily analyze and graph various types of functions, helping you solve problems and interpret mathematical data accurately.
Factoring Trinomials with Ease
Factoring trinomials is a key skill in simplifying expressions and solving equations. This process involves breaking down a three-term polynomial into two binomials that, when multiplied, result in the original expression. The ability to factor trinomials efficiently helps you solve quadratic equations and simplifies many types of algebraic problems.
The first step in factoring is identifying the structure of the trinomial, usually in the form of ax² + bx + c. Recognizing patterns between the coefficients allows you to find two numbers that multiply to give the constant term and add up to give the middle coefficient. Once you identify these two numbers, you can express the trinomial as the product of two binomials.
Here’s a basic strategy to factor a trinomial:
- Identify: Look for the structure ax² + bx + c.
- Find factors: Find two numbers that multiply to ac and add up to b.
- Rewrite: Split the middle term using the two numbers you found.
- Factor by grouping: Group the terms and factor out the common factors.
- Final factor: Express the trinomial as the product of two binomials.
With practice, recognizing these patterns becomes easier, allowing you to factor trinomials quickly and accurately. This skill is essential not only for simplifying expressions but also for solving quadratic equations and tackling more complex problems in mathematics.
Working with Rational Expressions and Equations
Rational expressions involve ratios of polynomials and can be simplified, added, subtracted, multiplied, or divided just like numerical fractions. Understanding how to manipulate these expressions is essential for solving a variety of problems, especially when dealing with real-world scenarios that involve rates, proportions, and relationships between variables. The key to working with rational expressions and equations is understanding the restrictions on the variables and ensuring that the denominator is never zero.
When performing operations with rational expressions, the process is similar to working with regular fractions, but with the added complexity of polynomials in the numerator and denominator. This requires factoring, finding common denominators, and simplifying complex expressions. Solving rational equations often involves cross-multiplication and isolating the variable to find its value.
Key Steps for Simplifying Rational Expressions

- Factor: Begin by factoring both the numerator and denominator, if possible.
- Cancel Common Factors: After factoring, cancel out any common factors between the numerator and denominator.
- Simplify: Perform any remaining operations to simplify the expression as much as possible.
Solving Rational Equations

When solving equations that contain rational expressions, you’ll need to follow a series of steps to isolate the variable and find the solution. Often, this includes eliminating the fractions by multiplying both sides of the equation by the least common denominator (LCD). It’s important to check for extraneous solutions, as certain values of the variable may result in division by zero.
- Multiply through by the LCD: Eliminate the denominators by multiplying both sides of the equation by the least common denominator.
- Solve the resulting equation: After removing the denominators, solve the simplified equation as you would any linear or quadratic equation.
- Check for extraneous solutions: Verify that the solutions do not make the denominator zero in the original equation.
Mastering these techniques will allow you to manipulate and solve rational expressions and equations with confidence, providing a solid foundation for more advanced mathematical topics.
Quadratic Equations and Their Solutions
Quadratic equations are a fundamental part of mathematics, representing relationships where the highest exponent of the variable is 2. These equations often describe parabolic curves when graphed and have a wide range of applications in fields like physics, engineering, and economics. Solving these equations allows you to find the values of the variable that satisfy the equation, known as the solutions or roots.
Quadratic equations typically have the form ax² + bx + c = 0, where a, b, and c are constants. There are several methods to solve these equations, each depending on the specific form of the equation and the values of the coefficients. These methods include factoring, completing the square, and using the quadratic formula. Understanding how to apply these techniques ensures that you can solve any quadratic equation, even if it appears complex.
Methods for Solving Quadratic Equations
There are three main techniques for solving quadratic equations, each useful depending on the structure of the equation:
- Factoring: If the quadratic can be factored into two binomials, set each factor equal to zero and solve for the variable.
- Completing the Square: Rearrange the equation to form a perfect square trinomial, then solve for the variable.
- Quadratic Formula: Use the formula x = (-b ± √(b² – 4ac)) / 2a to solve for the variable, regardless of whether the equation is factorable.
Understanding the Roots
The solutions to a quadratic equation are known as the roots, and they can be real or complex, depending on the value of the discriminant (b² – 4ac). If the discriminant is positive, there are two real solutions. If it is zero, there is one real solution, and if it is negative, the solutions are complex conjugates. Understanding the nature of the roots helps to interpret the equation’s solutions and their implications in real-world problems.
Mastering the methods for solving quadratic equations and understanding the properties of their solutions is an essential skill in mathematics that opens the door to solving more advanced problems.
Systems of Equations: Methods and Practice
Solving systems of equations is a crucial skill in mathematics, as it involves finding the values that satisfy two or more equations simultaneously. These systems can represent various types of relationships and are common in real-world problems where multiple factors interact. The goal is to determine the point or points where the equations intersect, which can be interpreted as the solution to the system.
There are several methods available to solve systems of equations, each with its advantages depending on the nature of the equations. The most common techniques include graphing, substitution, and elimination. Each method provides a different approach to finding the solution and can be chosen based on the complexity or form of the equations involved.
Common Methods for Solving Systems
- Graphing: This method involves plotting both equations on a coordinate plane. The point of intersection is the solution to the system.
- Substitution: In this method, one equation is solved for one variable, and then this expression is substituted into the other equation to find the value of the other variable.
- Elimination: By adding or subtracting the equations, terms with one variable are eliminated, allowing for the solution of the remaining variable.
Choosing the Best Method
The best method for solving a system of equations often depends on the specific characteristics of the equations. If the system is relatively simple and the equations can be easily graphed, the graphing method may be the quickest. For systems where one variable is easily isolated, substitution may be the most efficient. In cases where both variables are difficult to isolate, the elimination method may be preferable. Understanding when to use each technique will help you solve systems more effectively.
With practice, mastering these methods will allow you to solve systems of equations quickly and accurately, paving the way for more advanced problem-solving techniques in various mathematical fields.
Exploring Exponential Functions and Laws
Exponential functions are an essential part of mathematics, representing relationships where the rate of change of a variable is proportional to its current value. These functions are often used to model growth or decay processes in various fields, such as biology, economics, and physics. Understanding the properties of exponential functions and the laws that govern them is crucial for analyzing situations involving rapid changes, such as population growth, radioactive decay, and compound interest.
At the heart of exponential functions is the base, which determines how fast the function grows or decays. The most common exponential functions have a base of e (Euler’s number) or 10, although any positive number greater than 1 can serve as the base. Exponential functions follow a consistent pattern and exhibit certain laws that simplify their manipulation and solving. These laws provide a set of rules for working with exponents, helping to simplify complex expressions and equations.
Key Laws of Exponents
There are several fundamental laws of exponents that help to simplify operations involving exponential expressions. These laws apply to any base (except 0) and are essential when solving exponential equations:
| Law | Example | Explanation |
|---|---|---|
| Product Rule: am × an = am+n | 23 × 24 = 27 | When multiplying expressions with the same base, add the exponents. |
| Quotient Rule: am / an = am-n | 58 / 53 = 55 | When dividing expressions with the same base, subtract the exponents. |
| Power Rule: (am)n = am×n | (32)3 = 36 | When raising a power to another power, multiply the exponents. |
| Zero Exponent Rule: a0 = 1 | 70 = 1 | Any non-zero number raised to the zero power equals 1. |
Applications of Exponential Functions
Exponential functions are used to model a wide variety of real-world phenomena, particularly those involving growth or decay. Some common applications include:
- Population Growth: Exponential functions can model the rapid growth of populations over time, assuming a constant rate of increase.
- Radioactive Decay: Exponential decay is used to describe the rate at which radioactive substances lose their activity.
- Compound Interest: In finance, exponential functions are used to calculate the growth of investments over time with compound interest.
By mastering the laws of exponents and understanding the behavior of exponential functions, you’ll be able to solve a wide range of mathematical problems and apply these concepts to real-world situations involving growth, decay, and more.
Radical Expressions Simplified
Radical expressions involve roots, such as square roots, cube roots, and higher-order roots. Simplifying these expressions allows for easier manipulation and understanding, especially when solving equations or performing calculations. In many cases, the goal is to express a radical in a simpler form, removing any unnecessary complexity or irrational parts, which makes the expression easier to work with.
Simplifying radical expressions involves several strategies, including factoring, rationalizing the denominator, and reducing terms under the radical. The process typically requires identifying perfect squares, cubes, or higher powers to simplify the root, as well as using mathematical properties that apply to radicals. By following a systematic approach, complicated expressions can often be reduced to simpler forms that are more manageable.
Key Techniques for Simplification
- Factorization: Break down the number under the radical into its prime factors. If any factor is a perfect square or cube, take it outside the radical.
- Rationalizing the Denominator: When a radical appears in the denominator of a fraction, multiply both the numerator and denominator by a term that will eliminate the radical from the denominator.
- Combining Like Terms: When simplifying expressions with multiple radicals, combine terms that have the same radicand (the number under the root).
Example of Simplification
Consider the expression √72. To simplify it, we first factor 72 into prime factors: 72 = 36 × 2. Since 36 is a perfect square, we can take the square root of 36 outside the radical, leaving us with 6√2. This is the simplified form of √72.
By practicing these techniques, you will become more comfortable simplifying radical expressions and using them in various mathematical applications.
Mastering Word Problems in Algebra
Word problems often present mathematical challenges in the form of real-life scenarios, requiring you to translate the situation into mathematical expressions or equations. These problems can appear complex at first, but with a methodical approach, they become more manageable. The key to solving word problems lies in understanding the relationship between the quantities involved and how to represent them mathematically.
The first step in solving any word problem is carefully reading the question and identifying the important information. Once the relevant details are clear, the next task is to translate them into a solvable equation. Often, this requires breaking down the problem into smaller, more straightforward steps. With practice, identifying these steps becomes more intuitive, allowing for more efficient solutions.
To approach word problems effectively, consider the following tips:
- Identify key information: Extract the essential data points, such as numbers, units, and relationships between variables.
- Translate the words into math: Use variables to represent unknowns and create equations that reflect the relationships described in the problem.
- Solve step by step: Break the problem into manageable steps, solve for one unknown at a time, and ensure each step logically follows from the previous one.
- Check your work: Once you have an answer, plug it back into the original context of the problem to see if it makes sense.
With regular practice, word problems can become a less daunting task. The more you apply these strategies, the easier it will be to navigate complex scenarios and arrive at accurate solutions. Over time, your problem-solving skills will become more refined, making it easier to approach even the most challenging questions with confidence.
Interpreting and Using Algebraic Models
Mathematical models are powerful tools that represent real-world situations through numbers and relationships. By translating a problem into a mathematical expression or equation, you can solve it using various strategies. These models can describe patterns, predict outcomes, and provide insights into various phenomena. Understanding how to interpret and manipulate these models is essential for solving complex problems in everyday contexts.
The ability to work with these models involves recognizing the underlying structure of a situation and converting that structure into a mathematical form. This process often requires identifying variables, constants, and operations that define the relationship between different elements of the problem. Once a model is established, it can be used to make predictions, solve for unknowns, or analyze trends over time.
Key Steps in Using Mathematical Models
- Identify the variables: Determine which quantities in the problem are unknown or need to be measured.
- Set up the model: Translate the relationships and rules described in the problem into mathematical expressions or equations.
- Apply operations: Use algebraic operations to manipulate the model, solve for unknowns, and explore the solution.
- Interpret the results: Once you have a solution, check its relevance to the original situation and draw conclusions based on the findings.
Examples of Real-World Models
Mathematical models are widely used in various fields such as finance, science, engineering, and economics. For instance, a simple model might describe how the cost of a product changes over time, while more complex models can predict population growth or the spread of diseases. Understanding how to build and work with these models is a crucial skill in both academic and professional contexts.
How to Tackle Inequality Word Problems
Inequality word problems can seem tricky at first, but with a clear approach, they become manageable. These problems involve relationships where one quantity is either greater than, less than, or not equal to another. The key to solving these problems is understanding how to translate the words into mathematical expressions and then applying the appropriate operations to find the solution.
When dealing with inequality word problems, the process begins with identifying the important information from the question. You will need to recognize the conditions that involve greater than, less than, or equal to relationships. Once this is clear, you can set up an inequality to represent the situation and solve for the unknown. This often involves simple algebraic manipulation, just like solving equations, but with an added focus on the direction of the inequality sign.
Step-by-Step Approach
- Read the problem carefully: Pay attention to the language used to describe the relationships, such as “more than”, “less than”, “at least”, or “no more than”.
- Identify the variables: Determine what the unknown is and assign a variable to it.
- Set up the inequality: Translate the verbal expression into an inequality using the appropriate symbols for greater than, less than, etc.
- Solve the inequality: Use algebraic operations to isolate the variable and solve for its possible values. Be sure to reverse the inequality sign when multiplying or dividing by a negative number.
- Interpret the solution: After solving, check if the solution makes sense within the context of the problem and understand the possible range of values for the variable.
Examples of Inequality Word Problems
Let’s consider a simple example: “A school is selling tickets for a concert. The total amount raised from ticket sales must be at least $500. Each ticket costs $10. How many tickets must be sold?”
To solve this, you would set up the inequality: 10x ≥ 500, where x represents the number of tickets. After solving, you find that x ≥ 50. This means the school must sell at least 50 tickets to meet the goal. This type of solution shows how inequalities help determine limits or bounds in real-world scenarios.
Common Mistakes in Mathematics and How to Avoid Them
When working with mathematical concepts, many students encounter certain errors that can hinder their progress. These mistakes often arise from misunderstandings of fundamental principles or from rushing through calculations without careful thought. Recognizing these common pitfalls can help you avoid them and improve your problem-solving skills.
To enhance your understanding and accuracy, it’s important to be mindful of frequent missteps and adopt strategies to avoid them. Whether you’re simplifying expressions, solving equations, or interpreting word problems, staying alert to these errors will help you succeed in your studies.
Common Mistakes
- Neglecting to Distribute: One of the most frequent errors is forgetting to distribute a number or variable across terms inside parentheses. For example, in the expression 2(x + 3), failing to distribute the 2 properly results in 2x + 3 instead of the correct 2x + 6.
- Incorrect Sign Handling: When solving equations, especially when multiplying or dividing by negative numbers, students often forget to reverse the inequality sign or mismanage negative signs in terms. Always double-check operations that involve negatives.
- Overlooking Like Terms: Combining terms incorrectly is another common mistake. For instance, adding 2x + 3y together as if they are the same term will lead to an incorrect result. Be sure to combine only like terms.
- Skipping Steps: Rushing through problems can lead to skipping critical steps, such as simplifying before solving or improperly isolating variables. Always perform operations step by step to ensure clarity and correctness.
- Incorrectly Interpreting Word Problems: Word problems often involve setting up an equation or inequality based on a description. A common mistake is misunderstanding the relationship between variables or misinterpreting key phrases. Carefully read each word problem and highlight key information before translating it into a mathematical model.
How to Avoid These Mistakes
- Double-check work: After completing each step, quickly review your calculations and make sure they are correct.
- Take your time: Avoid rushing through problems. Methodically work through each part to ensure all operations are accurate.
- Practice regularly: The more you practice, the more familiar you’ll become with common patterns, and the better you’ll recognize where mistakes tend to occur.
- Ask for help: If you’re unsure about a step or rule, seek clarification from a teacher or tutor. Sometimes a fresh perspective can make all the difference.
By understanding and addressing these common errors, you can significantly improve your skills and approach to mathematical problems, ensuring that your solutions are correct and well-executed.
Tips for Efficient Exam Preparation
Preparing for an important test requires more than just reviewing materials at the last minute. Success in exams is largely influenced by effective time management, understanding key concepts, and practicing problem-solving techniques. To optimize your preparation, it’s crucial to adopt strategies that enhance focus and retention, while also minimizing stress.
By organizing your study schedule, actively engaging with the content, and practicing under exam conditions, you can build confidence and improve your ability to perform under pressure. Here are some practical tips to help you get the most out of your preparation time.
Organize Your Study Schedule

- Break Down Topics: Divide your study material into manageable sections, focusing on one topic at a time. This will help you avoid feeling overwhelmed and ensure you cover all necessary content.
- Set Realistic Goals: Establish clear, achievable goals for each study session. Make sure to review and reinforce what you have learned regularly, rather than cramming the night before.
- Prioritize Difficult Areas: Identify your weaker areas and allocate more time to them. Tackling the hardest material first allows you to focus when you’re most alert and saves easier topics for later.
Practice and Review
- Practice Regularly: The more you practice, the more confident you’ll become. Work through sample problems, quizzes, or past tests to familiarize yourself with the format and types of questions you might encounter.
- Simulate Test Conditions: Practice solving problems under timed conditions. This will help you improve your speed and manage your time effectively during the real exam.
- Review Mistakes: After practicing, take the time to go over any errors and understand where you went wrong. Correcting mistakes reinforces learning and prevents them from recurring on the exam.
Stay Focused and Relaxed
- Avoid Distractions: Create a quiet, distraction-free study environment. Turn off your phone, social media, or anything else that might take your attention away from your studies.
- Take Breaks: Long study sessions can be draining. Schedule short breaks to recharge your mind, which will help you retain more information and stay productive.
- Maintain a Positive Mindset: Stay calm and confident. Anxiety can negatively impact your performance, so take deep breaths and remember that you are well-prepared.
By following these strategies and staying disciplined in your approach, you can maximize your chances of success and feel prepared for the challenges ahead. Efficient exam preparation is about working smarter, not harder, and giving yourself the tools to succeed on the test day.