
In this section, we will explore various important topics covered in the first level of advanced mathematics. It aims to provide you with a deeper understanding of essential principles that form the foundation of more complex concepts. Whether you’re looking to sharpen your problem-solving skills or reinforce your knowledge, this guide is designed to help you navigate through these core ideas with ease.
By breaking down the material into manageable steps, we’ll ensure that each concept is presented in a way that’s easy to follow. You’ll find practical examples that show how to apply different strategies, making the learning process more intuitive. The goal is not only to solve problems but also to gain a stronger grasp of underlying techniques that will benefit you in future studies.
This guide will be especially useful for anyone seeking to improve their grasp of mathematical reasoning and gain confidence in approaching similar challenges. By focusing on key problem-solving methods and their real-world applications, you’ll be able to build a solid base that can be expanded in later stages of learning.
Understanding Key Solutions and Strategies
This section provides a comprehensive guide to solving problems and mastering the essential concepts typically found in the first stage of advanced coursework. By focusing on core skills, this guide helps learners break down complex challenges into simpler, more manageable steps. Each solution is explained thoroughly, ensuring clarity in both approach and methodology.
Key Steps for Effective Problem Solving
To tackle any problem effectively, it’s essential to follow a structured approach. Here are some key steps to keep in mind:
- Read the problem carefully to understand the given information.
- Identify the unknowns and what needs to be solved.
- Apply relevant strategies and formulas where necessary.
- Check your solution to ensure accuracy.
- Review the steps taken to ensure the correct method was followed.
Common Problem Types and Solutions
In this guide, we also address several common problem types you’ll encounter. Each example is explained with a step-by-step solution:
- Linear equations: Methods for solving basic linear equations, including isolating variables and simplifying expressions.
- Word problems: Techniques for translating word problems into mathematical expressions, then solving them methodically.
- Graphical solutions: Analyzing and interpreting graphs to solve equations visually.
- Fractions and decimals: Strategies for working with fractions, decimals, and conversions between them.
Each solution is designed to build confidence and develop a deeper understanding of the underlying techniques, ensuring long-term success in further studies.
Key Concepts in Module 6
This section focuses on the fundamental ideas and principles that are essential for mastering the first level of advanced coursework. By understanding these core concepts, learners can build a strong foundation for more complex topics in the future. These concepts play a vital role in developing problem-solving skills and logical reasoning abilities.
Core Principles to Master
Several important ideas are explored in this section, each serving as a building block for success:
- Understanding Variables: Learn how to work with variables and their relationships within expressions and equations.
- Operations and Their Properties: Explore the fundamental operations–addition, subtraction, multiplication, and division–and their properties.
- Linear Relationships: Study the principles of linear relationships and how they are expressed and solved algebraically.
- Graph Interpretation: Develop skills in analyzing and interpreting data presented through graphs, including linear and non-linear functions.
- Fractions and Ratios: Master techniques for working with fractions, simplifying ratios, and converting between different formats.
Building Logical Thinking
Along with mastering these core ideas, it’s essential to develop logical thinking through systematic approaches to problem solving. By practicing these techniques, learners will be able to tackle increasingly difficult problems with confidence. Key strategies include:
- Breaking Down Complex Problems: Divide larger problems into smaller, simpler parts to make them more manageable.
- Identifying Patterns: Recognize recurring patterns to apply efficient solutions and predict outcomes.
- Using Real-Life Applications: Connect abstract concepts to practical, real-world scenarios for better understanding.
By focusing on these foundational ideas, learners will gain a deeper insight into mathematical thinking and be better prepared for the challenges ahead.
Understanding Problem Solving Techniques
Problem solving is a critical skill that allows learners to approach challenges with a structured and methodical strategy. It involves breaking down complex issues into smaller, more manageable parts and applying logical reasoning to find solutions. Mastering these techniques not only helps in academic studies but also enhances critical thinking abilities that are valuable in real-life situations.
There are several effective approaches to solving problems, each focusing on simplifying the task and reducing the chances of error. These techniques encourage a clear thought process, ensuring that each step is carefully considered and executed.
One key aspect of problem solving is understanding the type of problem you’re dealing with. Whether it involves equations, geometric shapes, or data analysis, recognizing the problem’s structure helps in selecting the most appropriate method. After identifying the problem type, it’s important to:
- Analyze the given information: Carefully read the problem to understand what is provided and what needs to be determined.
- Plan a solution strategy: Decide on the method or formula to use and how the information can be manipulated.
- Execute the plan: Carry out the necessary calculations or steps systematically to reach the solution.
- Verify the result: After solving, check if the solution makes sense in the context of the problem.
Through consistent practice and application of these techniques, learners can build confidence and accuracy in solving a wide range of challenges. The key is to approach each problem with a calm, methodical mindset and avoid rushing through the steps.
Step-by-Step Guide to Module 6
This guide provides a clear and structured approach to mastering the key concepts in the sixth unit of your course. By following each step, learners can gradually build their understanding and confidently tackle the problems presented. The goal is to break down each topic into manageable sections, offering practical tips and methods to ensure a thorough understanding of the material.
Breaking Down the Concepts

The first step in any learning process is to break down the content into smaller, more understandable pieces. For this unit, we begin with the foundational concepts that will be used throughout the lessons. Start by focusing on the basic principles and try to understand how they relate to one another:
- Identify key formulas and definitions: Recognizing the core formulas early on will help you apply them more easily later.
- Understand relationships between variables: Work on understanding how different elements of an equation or graph interact.
- Practice simple examples: Begin with easier examples to build confidence before moving on to more complex ones.
Practical Application and Practice
Once you’ve grasped the basic concepts, it’s time to put them into practice. Here’s how to approach problem-solving effectively:
- Apply learned techniques: Use the formulas and strategies you’ve learned to solve problems, ensuring that each step is clear and logical.
- Double-check your solutions: Always review your calculations and answers to ensure they are correct.
- Seek additional problems: Reinforce your learning by solving extra practice questions and challenges.
By following this step-by-step process, learners can gradually build expertise and become proficient in solving problems related to this unit. Taking your time with each concept will pay off in the long run, making future topics easier to grasp.
How to Approach Algebraic Equations
Solving algebraic equations involves finding the unknown values that satisfy a given relationship. To effectively solve these types of problems, it’s crucial to follow a clear and systematic approach. By breaking down each equation into manageable steps, you can confidently work through the solution process without becoming overwhelmed.
The key to solving equations is understanding how to manipulate them to isolate the unknown variable. This requires familiarity with basic algebraic rules and operations such as addition, subtraction, multiplication, and division. Once you’re comfortable with these, the next step is to apply them in a logical order to solve for the unknown.
Here’s a simple strategy to follow when working with algebraic equations:
- Identify the equation type: Determine if it’s a linear equation, quadratic, or another form. This will help you choose the right method for solving it.
- Simplify both sides: Combine like terms and eliminate unnecessary constants or coefficients to make the equation easier to solve.
- Isolate the variable: Perform inverse operations to move terms involving the unknown variable to one side of the equation.
- Check your solution: Once you’ve isolated the variable, substitute the solution back into the original equation to ensure it works.
With consistent practice, solving algebraic equations becomes an intuitive process. By following these steps, learners can build confidence in their problem-solving abilities and gradually tackle more complex equations with ease.
Mastering Fractions in Module 6
Working with fractions can initially seem challenging, but with the right techniques, it becomes an essential skill in solving many types of problems. This section focuses on understanding the core concepts of fractions, including operations such as addition, subtraction, multiplication, and division. Mastering these fundamental skills will make working with fractions more intuitive and help you apply them to various problem types.
To begin mastering fractions, it’s important to understand their basic structure and how they relate to whole numbers. Fractions represent parts of a whole, and performing operations with them requires careful attention to common denominators and numerators. By learning how to manipulate fractions, you’ll be able to solve more complex equations and real-world problems involving proportions and ratios.
Key Steps for Working with Fractions
Here are some essential steps to follow when working with fractions:
- Identify and simplify fractions: Always check if a fraction can be simplified by dividing both the numerator and denominator by their greatest common divisor (GCD).
- Find a common denominator: When adding or subtracting fractions, ensure that the denominators are the same. This often involves finding the least common denominator (LCD).
- Convert improper fractions: If you end up with an improper fraction (where the numerator is greater than the denominator), convert it to a mixed number if needed.
- Multiply and divide: When multiplying fractions, simply multiply the numerators and denominators. For division, multiply by the reciprocal of the second fraction.
Practical Tips for Fractions
Applying fractions in real-world situations becomes much easier when you practice consistently. Here are some practical tips:
- Work on word problems: Practice converting word problems into fraction-based equations. This will help you see how fractions are used in everyday situations like recipes, measurements, and finance.
- Check for simplifications: Always look for opportunities to reduce fractions to their simplest form, which can make calculations easier.
- Use visual aids: Drawing fraction bars or pie charts can help you visualize how fractions work and make it easier to perform operations.
With these strategies, you’ll be able to tackle a wide range of fraction-related problems with confidence. Consistent practice and understanding the underlying concepts are key to mastering this essential skill.
Common Mistakes in Module 6
When working through problems in this section, learners often make a few common errors that can lead to incorrect answers. Recognizing these mistakes and understanding how to avoid them is key to mastering the material. This section highlights some of the most frequent pitfalls and offers guidance on how to tackle them effectively.
One of the primary challenges is the misinterpretation of problems or overlooking small details. Often, students may rush through steps or fail to double-check their work, which leads to avoidable mistakes. By slowing down and following a systematic approach, these errors can be minimized.
Typical Errors and How to Avoid Them
Here are some of the most common mistakes and tips on how to avoid them:
- Incorrectly applying operations: When dealing with fractions or algebraic expressions, students sometimes confuse the rules for addition, subtraction, multiplication, and division. Always remember to follow the proper order of operations (PEMDAS).
- Forgetting to simplify: After performing operations on fractions, many forget to simplify their results to the lowest terms. Always check if a fraction can be reduced by finding the greatest common divisor (GCD).
- Not finding a common denominator: In fraction addition or subtraction, failing to find a common denominator can lead to incorrect results. Make sure to convert fractions so that their denominators match before performing the operation.
- Misplacing negative signs: Neglecting the proper placement of negative signs in equations can lead to incorrect answers. Double-check every step where negative numbers are involved.
- Skipping steps: Rushing through the problem-solving process can cause important steps to be missed. It’s essential to take the time to break the problem into smaller parts and follow each step carefully.
Tips for Error-Free Problem Solving
To avoid these common mistakes and improve accuracy, consider the following tips:
- Read carefully: Always read the problem thoroughly to understand what is being asked before jumping into the solution process.
- Show your work: Writing out every step, even if it seems obvious, helps to ensure that no steps are skipped and mistakes are caught early.
- Double-check your answers: After solving a problem, go back and check your work, especially in more complex problems where errors are more likely.
By being aware of these common mistakes and practicing careful attention to detail, learners can avoid many of the errors that hinder progress and improve their overall understanding of the material.
Real-World Applications of Math 1
The concepts explored in this section are not only important for academic success but also play a crucial role in solving real-world problems. The skills learned here have practical applications in various fields, from budgeting to engineering. By understanding how to apply these concepts outside the classroom, you can gain a deeper appreciation for their relevance and usefulness in everyday life.
In this section, we’ll explore how the skills developed in this course can be used in various professions and real-life situations. From managing finances to designing structures, the ability to work with numbers and solve problems is a valuable tool in many aspects of life.
Practical Uses in Daily Life
Here are some ways the concepts from this section can be applied in real-world situations:
- Budgeting and Personal Finance: Understanding percentages and fractions is essential when creating a budget, calculating interest rates, and managing expenses.
- Construction and Engineering: When designing buildings or other structures, knowledge of measurements, proportions, and basic algebra is crucial to ensure accuracy and safety.
- Cooking and Recipe Adjustments: Fractions and ratios are frequently used in cooking when adjusting portion sizes or converting measurements.
- Sports and Fitness: Whether it’s calculating statistics, tracking performance, or understanding scoring systems, mathematical concepts are frequently applied in sports analysis.
Applications in Various Careers
Beyond daily life, mathematical skills are also vital in a range of careers. Some professions where these concepts are highly relevant include:
- Finance and Accounting: Accountants and financial analysts use algebra and arithmetic to calculate budgets, profit margins, and taxes.
- Engineering: Engineers rely on mathematical concepts such as geometry and algebra to design and construct buildings, bridges, and machinery.
- Healthcare: Medical professionals use math for dosage calculations, analyzing health data, and managing patient care metrics.
- Technology: Software developers and IT professionals use algorithms, logic, and problem-solving techniques to create programs and troubleshoot technical issues.
By mastering the concepts from this section, you gain valuable skills that can be applied across various professions and everyday activities. The ability to solve practical problems using mathematical principles is an essential skill in both personal and professional settings.
Tips for Studying Math Effectively
Studying mathematical concepts can sometimes feel challenging, but with the right approach, you can improve your understanding and mastery of the subject. Effective studying isn’t just about memorizing formulas or solving problems–it’s about developing a deeper comprehension and learning how to apply your knowledge in different situations. The key to success lies in consistency, problem-solving techniques, and active engagement with the material.
In this section, we’ll explore some practical tips that will help you study more efficiently and gain a stronger grasp of the concepts. Whether you’re preparing for an exam or trying to improve your problem-solving abilities, these strategies will enhance your overall study routine.
Effective Study Habits
Here are some helpful practices to integrate into your study routine:
| Tip | Description |
|---|---|
| Practice Regularly | Consistent practice is key to mastering mathematical concepts. Set aside time every day to work on problems, review notes, and reinforce your understanding. |
| Understand the Concepts | Instead of memorizing formulas, focus on understanding the logic behind them. Grasping the ‘why’ will make it easier to apply the rules in different scenarios. |
| Work on Mistakes | Don’t just move on when you make an error. Take the time to understand what went wrong and how to avoid similar mistakes in the future. |
| Use Visual Aids | Visualizing problems with diagrams, charts, or graphs can help you better understand abstract concepts and make solving problems easier. |
| Break Down Complex Problems | For difficult problems, break them down into smaller, more manageable steps. This makes it easier to identify where you’re going wrong and stay on track. |
Additional Strategies for Success
In addition to the basic study habits, consider incorporating the following strategies to boost your learning:
- Teach Others: Teaching a concept to someone else is one of the best ways to reinforce your own understanding. Explaining ideas clearly shows where you may need more practice.
- Group Study: Collaborating with peers can provide new insights and help you tackle problems from different perspectives.
- Use Online Resources: Online tutorials, videos, and forums can offer explanations, alternative methods, and solutions to problems that might be confusing.
- Stay Organized: Keep track of important formulas, notes, and problems. Organizing your study materials will make review sessions more efficient.
By applying these study techniques, you’ll find yourself becoming more confident and capable in your ability to tackle mathematical challenges. Remember, regular practice and a solid understanding of the material are the foundations of success in this subject.
Understanding Graphs and Functions

Graphs and functions are essential tools for visualizing relationships between variables and solving problems. Understanding how to interpret and create graphs helps you better analyze real-world situations, while mastering functions provides a foundation for solving complex equations and predicting outcomes. These concepts are deeply connected, as graphs often represent the behavior of functions in a visual format.
In this section, we’ll explore how to interpret different types of graphs, understand the concept of functions, and apply these skills to solve practical problems. By the end, you’ll have a clearer understanding of how these mathematical tools can help you make sense of data and relationships in everyday life.
Key Concepts of Functions and Graphs
Here are some important concepts to understand when studying functions and graphs:
| Concept | Description |
|---|---|
| Functions | A function is a relationship between two variables where each input (x) is related to exactly one output (y). This relationship can be expressed in equations, tables, or graphs. |
| Domain and Range | The domain is the set of all possible input values (x), while the range is the set of all possible output values (y) resulting from the function. |
| Linear Functions | Linear functions create straight-line graphs, where the rate of change between variables is constant. These functions are represented by equations of the form y = mx + b. |
| Non-Linear Functions | Non-linear functions create curved graphs, where the rate of change is not constant. Examples include quadratic and exponential functions. |
| Graph Interpretation | Interpreting graphs involves analyzing the shape and direction of the curve to understand the relationship between variables. Key features include the slope, intercepts, and turning points. |
By recognizing these basic principles, you can begin to understand how different types of graphs represent functions, and how to manipulate them for problem-solving.
Practical Applications of Graphs and Functions
Graphs and functions have numerous applications in various fields. For example:
- Economics: Graphs are used to analyze trends, such as supply and demand, while functions help model cost and revenue predictions.
- Science: Functions and graphs are used to model phenomena like growth rates, temperature changes, and chemical reactions.
- Engineering: Engineers use graphs to represent the relationship between forces, distances, and time, helping them optimize designs.
- Statistics: Data is often represented using graphs, allowing statisticians to identify patterns and make predictions based on observed trends.
By mastering graphs and functions, you’ll be equipped to analyze data, make informed decisions, and solve complex problems with confidence.
How to Simplify Expressions
Simplifying expressions is a crucial skill that helps you make complex mathematical statements more manageable and easier to solve. The process involves reducing an expression to its simplest form by combining like terms, removing parentheses, and applying the necessary rules of arithmetic operations. By mastering this technique, you can make calculations faster and more accurate, while also gaining a deeper understanding of the underlying structure of algebraic expressions.
In this section, we will guide you through the key steps and strategies involved in simplifying expressions, covering everything from basic arithmetic to more advanced concepts. Whether you’re dealing with numbers, variables, or both, these methods will help you approach problems with clarity and confidence.
Step-by-Step Process for Simplification
Follow these steps to simplify any given expression:
- Identify Like Terms: Look for terms that have the same variable raised to the same power. Only terms with matching variables and exponents can be combined.
- Combine Like Terms: Add or subtract the coefficients of like terms. For example, in the expression 3x + 4x, combine the terms to get 7x.
- Distribute (If Necessary): Use the distributive property to eliminate parentheses. For example, in the expression 2(x + 3), distribute the 2 to both terms inside the parentheses, resulting in 2x + 6.
- Perform Arithmetic Operations: Simplify any remaining numbers by performing addition, subtraction, multiplication, or division as needed.
- Check for Further Simplification: After combining like terms and simplifying, ensure there are no further terms that can be simplified.
By following these basic steps, you can simplify almost any expression and make it easier to work with in equations or other mathematical operations.
Examples of Simplified Expressions
Here are a few examples of simplified expressions:
- Example 1: 5x + 3x = 8x
- Example 2: 2(x + 4) = 2x + 8
- Example 3: 3a + 4b – 2a = a + 4b
These examples demonstrate how combining like terms and applying basic operations can significantly simplify an expression.
Mastering this process is essential for solving more complex problems and preparing for more advanced topics in mathematics. By practicing simplification regularly, you’ll become more efficient in handling algebraic tasks and improve your problem-solving abilities.
Solving Word Problems with Ease
Word problems can often seem intimidating, but with the right approach, they become much more manageable. The key to solving these types of problems is understanding how to translate a real-world scenario into a mathematical expression. Once you can break down the problem into its essential components, you can apply the appropriate methods to find a solution.
This section provides strategies for tackling word problems step-by-step, enabling you to approach each problem with confidence. The goal is to equip you with tools that will help simplify complex scenarios and make it easier to navigate through different types of questions.
Steps to Solve Word Problems
Follow these steps to approach word problems systematically:
- Read the Problem Carefully: Pay close attention to the details, as word problems often include important information that can guide your solution.
- Identify the Question: Focus on what the problem is asking. This will help you understand what you need to find.
- Translate the Words into Math: Convert the information from the word problem into a mathematical equation or expression. Identify key operations such as addition, subtraction, multiplication, or division.
- Choose the Right Method: Decide which mathematical method is most appropriate for solving the equation based on the information you’ve gathered.
- Solve and Interpret: Perform the necessary calculations to solve the problem. Once you have the answer, make sure to interpret the result in the context of the original problem.
Example of a Word Problem Solution
Let’s look at an example to see how this process works in practice:
Problem: A store sells pens for $2 each and notebooks for $5 each. If you buy 3 pens and 2 notebooks, how much will the total cost be?
Solution:
- Read the problem: We know the price of each item and the number of items purchased.
- Identify the question: We need to find the total cost.
- Translate into math: Total cost = (3 pens × $2) + (2 notebooks × $5).
- Solve: Total cost = 6 + 10 = $16.
The total cost for purchasing 3 pens and 2 notebooks is $16.
By breaking down word problems in this way, you’ll find that they become less challenging and more straightforward to solve. The key is to practice these techniques, so they become second nature when faced with similar questions in the future.
Review of Key Learning Outcomes
At the conclusion of this unit, it is important to reflect on the essential concepts and skills that have been acquired. Reviewing the key learning outcomes helps solidify understanding and ensures that the critical topics have been grasped thoroughly. This process allows students to assess their progress and identify areas that may require further attention.
The primary focus of this review is to revisit the core ideas that were covered, emphasizing the practical application of these concepts in solving real-world problems. By revisiting these outcomes, learners can better connect abstract principles with tangible results, reinforcing their problem-solving abilities and mathematical reasoning.
Core Topics Covered
Throughout this section, several important areas have been explored. These topics include:
- Understanding Variables and Equations: Learning how to manipulate variables within equations and understanding their relationships.
- Solving Linear Equations: Mastering techniques to solve linear equations with one or more variables.
- Working with Fractions: Gaining a strong foundation in simplifying, adding, subtracting, and comparing fractions.
- Interpreting Word Problems: Developing skills to translate real-world situations into mathematical expressions and solve them effectively.
- Graphing and Functions: Acquiring the ability to graph linear equations and understand the relationship between variables through graphical representation.
Key Skills and Applications
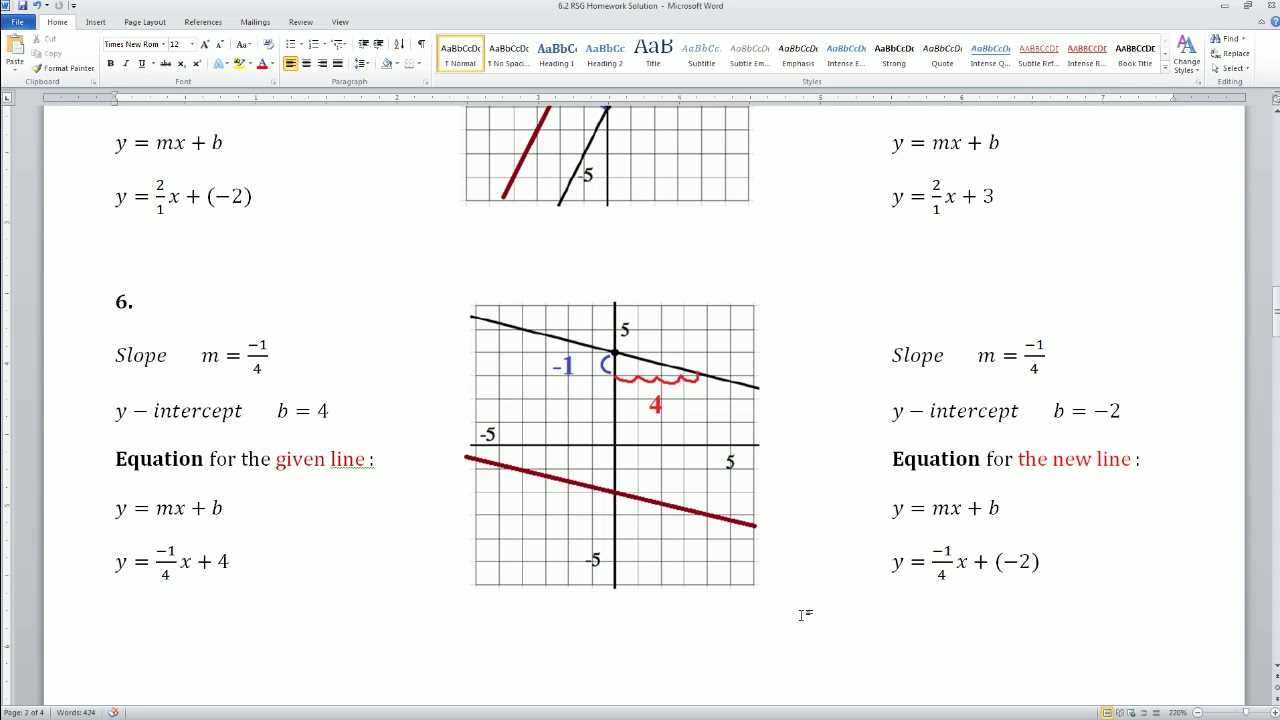
In addition to mastering theoretical concepts, this unit has helped strengthen key skills such as:
- Critical Thinking: Developing the ability to approach complex problems with a logical mindset and break them down into manageable steps.
- Problem Solving: Gaining experience in tackling various types of mathematical problems and applying the right techniques to find solutions.
- Real-World Application: Connecting mathematical principles to everyday situations and recognizing how they can be applied to solve practical challenges.
By reviewing these learning outcomes, students can reinforce their understanding and be better prepared for the next stage of their mathematical journey. Continuous practice and application of these principles will help ensure that the concepts are retained and ready for future use.
Exploring Geometry in Module 6
In this section, we delve into the fascinating world of geometric concepts and their applications. Understanding the fundamental properties of shapes, angles, and spatial relationships is essential in building a strong foundation for more advanced mathematical topics. Geometry provides the tools needed to analyze and solve real-world problems, from architecture to navigation.
This part of the curriculum focuses on key geometric principles, including the study of angles, triangles, quadrilaterals, and circles. By examining these shapes and their properties, students gain insight into their characteristics and how they interact within different contexts. Understanding geometric relationships also lays the groundwork for solving problems that involve measurement, area, and volume.
Key Concepts in Geometry
Several crucial topics in geometry are explored in this section:
- Angles and Their Relationships: Learning about acute, obtuse, and right angles, as well as complementary and supplementary angles, and their role in solving geometric problems.
- Triangles and Their Properties: Studying different types of triangles (equilateral, isosceles, scalene) and applying the Pythagorean theorem to solve problems involving right triangles.
- Quadrilaterals and Polygons: Exploring the properties of squares, rectangles, parallelograms, and other polygons, and learning how to calculate their area and perimeter.
- Circles and Arcs: Understanding the relationships between the radius, diameter, and circumference of a circle, and how to find the area of a circle.
Real-World Applications of Geometry
Geometry is not just a theoretical subject; its principles are used extensively in everyday life. Some practical applications include:
- Architecture and Design: Architects use geometric principles to create blueprints for buildings, ensuring structural integrity and aesthetic appeal.
- Navigation and Mapping: Geometric concepts such as distance, angles, and coordinates are vital in the fields of navigation and map-making.
- Engineering: Engineers rely on geometry to design products and systems, from bridges to vehicles, making sure that components fit together accurately.
By mastering these geometric principles, students not only improve their mathematical skills but also gain valuable tools for solving real-world problems. Geometry plays a crucial role in helping us understand the world around us and design solutions to complex challenges.
Test Preparation for Math 1
Preparing for an exam in mathematics involves more than just reviewing notes; it requires a strategic approach to understand key concepts, practice problem-solving techniques, and reinforce areas of difficulty. Success on assessments relies on familiarity with the material, confident application of learned skills, and effective time management during the test.
In this section, we will discuss practical steps to help you prepare for your exam effectively. By focusing on core topics, practicing with sample questions, and using different study techniques, you can approach your test with greater confidence and a solid grasp of the material. Whether you’re reviewing algebraic expressions, geometric principles, or solving real-world problems, effective preparation is key to achieving a high score.
Key Strategies for Test Preparation
- Review Core Concepts: Focus on the fundamental ideas covered in the curriculum, such as basic algebra, geometry, and number operations. Understanding the concepts thoroughly is essential for tackling any type of problem.
- Practice Regularly: Consistent practice is crucial for improving problem-solving speed and accuracy. Work through example problems, and make use of practice tests to simulate exam conditions.
- Identify Weak Areas: Pay attention to the topics that challenge you the most. Focus your study sessions on these areas, whether it’s solving equations, graphing functions, or working with fractions.
- Use Study Tools: Leverage study aids like flashcards, review sheets, and online resources. These can help reinforce your memory and provide a different perspective on difficult concepts.
Effective Time Management During Study
Managing your time during preparation is just as important as the actual study process. Here are some tips to optimize your study time:
- Set a Study Schedule: Break your study sessions into manageable blocks. Dedicate specific times each day to focus on different topics.
- Prioritize Important Topics: Spend more time on areas that are heavily weighted in the exam or where you struggle the most.
- Avoid Cramming: Try not to leave studying until the night before the test. Consistent review over a longer period is much more effective.
By following these tips, you will be better equipped to manage your time and efforts while preparing for the test. With proper preparation, you will approach your exam with the skills and confidence necessary to perform at your best.
Additional Resources for Extra Practice
To solidify your understanding and enhance your problem-solving skills, it’s essential to supplement your study routine with extra practice. There are various resources available that provide a wealth of exercises and explanations, helping to reinforce key concepts and boost your confidence. Whether you prefer interactive platforms, textbooks, or educational websites, these tools can provide the practice needed to master challenging topics.
In this section, we will explore a range of resources that cater to different learning styles. From online practice problems to video tutorials and printable worksheets, these additional materials can offer diverse ways to approach difficult topics and gain a deeper understanding of the material.
Online Platforms for Practice
- Interactive Websites: Websites like Khan Academy, IXL, and Brilliant offer interactive lessons and quizzes that allow you to practice key concepts at your own pace.
- Practice Apps: Mobile apps such as Photomath or Wolfram Alpha provide solutions and step-by-step explanations, which can help clarify difficult problems.
- Online Quizzes: Platforms like Quizlet and Quizizz offer a wide range of quizzes created by educators and students, allowing you to test your knowledge on various topics.
Printable Worksheets and Textbooks
- Workbooks: Printed workbooks, often available in bookstores or online, offer structured exercises that help you practice different types of problems.
- Textbook Exercises: Many textbooks come with end-of-chapter exercises or online resources that provide additional problems for practice.
- Custom Worksheets: Websites like Math-Aids.com and K5 Learning allow you to generate custom worksheets based on specific topics or problem types.
Utilizing these resources will allow you to practice regularly and ensure you are fully prepared to tackle any challenges that arise during your studies. By integrating extra practice into your routine, you will not only improve your proficiency but also build the confidence needed to excel in assessments.