
Preparing for a major assessment in mathematics requires a solid grasp of fundamental concepts and a clear understanding of how to apply them. A structured approach to reviewing past problems can significantly enhance your ability to solve similar challenges with ease. This section focuses on mastering the necessary skills and strategies to navigate complex questions, ensuring a more confident performance.
By examining various problem-solving methods and exploring common errors, you’ll gain insights into effective techniques for tackling each question. This will help you improve not only your accuracy but also your overall comprehension of the subject. Emphasizing logical thinking and step-by-step analysis, these insights will guide you toward success.
Review for Algebra 1 Midterm Exam Answer Key
In this section, we will focus on analyzing solutions to common problems encountered during a mathematics test. The primary objective is to break down each solution step by step, identifying key techniques and understanding the logic behind each calculation. This will help you see how to approach similar challenges with more clarity and confidence.
Understanding the methodology used to arrive at each result is essential for reinforcing your skills and avoiding common mistakes. Below is a breakdown of useful strategies and concepts that can be applied to a wide range of problems:
- Step-by-step problem solving: Begin by understanding the core concept being tested. Break down each part of the problem into smaller, more manageable steps to ensure accuracy.
- Recognizing common patterns: Many problems follow familiar patterns or formulas. Once you identify the pattern, applying the correct formula or method becomes easier.
- Avoiding common pitfalls: Watch out for misinterpretations of the question, overlooked details, or small calculation errors that can lead to incorrect answers.
- Checking your work: Once you arrive at a solution, review each step to verify its accuracy. This process helps catch errors and reinforces your understanding of the material.
Additionally, it’s important to practice regularly. The more you familiarize yourself with various types of problems, the more comfortable you’ll become with tackling them on the test. Repetition will solidify your grasp on the material and build your confidence.
By the end of this section, you should feel better equipped to understand and apply the concepts tested, giving you a clearer path toward achieving the best possible results.
Understanding Key Algebraic Concepts

Mastering the fundamental principles of mathematics is essential to solving complex problems with confidence. This section explores the most important techniques and ideas that form the foundation of solving equations, working with variables, and manipulating expressions. Understanding these concepts will enhance your ability to approach a variety of problems efficiently and accurately.
Core ideas to focus on include:
- Equations and variables: The relationship between unknown values and how to represent them using symbols. Understanding how to isolate and solve for variables is key to progressing in any problem.
- Operations with numbers: Addition, subtraction, multiplication, and division are the building blocks of all mathematical computations. Mastery of these operations in different contexts is crucial for solving a wide range of challenges.
- Factoring: Breaking down expressions into simpler components is a powerful tool. Recognizing when and how to factor is essential for simplifying complex problems.
- Functions and graphs: Understanding how to interpret and graph functions allows you to visualize relationships between variables and make more informed decisions when solving equations.
These core principles, when well understood, allow you to confidently tackle mathematical challenges and recognize patterns that appear throughout the material. The more you familiarize yourself with these concepts, the better prepared you will be to apply them in a variety of scenarios.
Common Mistakes in Algebra 1 Exams
In any mathematics test, it’s easy to make small errors that can significantly impact the final result. Recognizing these common pitfalls and understanding how to avoid them is crucial for improving your performance. In this section, we will explore some of the most frequent mistakes students make when solving problems and how to address them effectively.
Misinterpreting the Problem
One of the most frequent mistakes is misunderstanding what the question is asking. Often, it’s tempting to jump straight into calculations without fully comprehending the requirements. Taking a moment to carefully read the problem, identifying key information and what is being asked, can prevent this mistake.
- Rushing through word problems: Skimming over the text can lead to missing important details or misinterpreting variables.
- Overlooking negative signs: Forgetting to apply negative signs correctly when solving equations can lead to completely incorrect answers.
- Ignoring units of measurement: Not paying attention to units in word problems may cause confusion, especially when dealing with real-world applications.
Calculation Errors

Even if the problem is understood, simple calculation errors are a common issue. This includes mistakes in adding, subtracting, multiplying, or dividing numbers. These small errors can lead to incorrect results, even if the problem-solving process was otherwise correct.
- Careless arithmetic mistakes: These often occur when working too quickly or skipping steps.
- Incorrect distribution: When expanding expressions, it’s easy to forget to distribute terms correctly, leading to wrong answers.
- Misplacing decimal points: Decimal placement can make a huge difference, especially when working with fractions or percentages.
Being aware of these common mistakes and taking steps to avoid them can help reduce errors and improve accuracy in solving problems. Consistent practice and double-checking your work can make a significant difference in your performance.
How to Use the Answer Key Effectively

When preparing for a mathematics test, it’s important to understand how to use provided solutions as a learning tool rather than just a way to check your work. By carefully analyzing the provided solutions, you can uncover valuable insights into the problem-solving process, recognize patterns, and identify areas where you might need further improvement.
One effective approach is to compare each step of your solution with the correct process outlined in the provided solutions. This allows you to identify where your reasoning may have gone off track or where you missed an important step. It’s essential to focus on understanding why the correct solution works, rather than simply memorizing the result.
Additionally, it’s helpful to work through the problems on your own first before looking at the solutions. This ensures that you’re actively engaging with the material and testing your understanding before seeing the correct answers. Afterward, analyze any discrepancies between your approach and the correct method to better grasp the reasoning behind the correct answers.
By using the provided solutions as a tool for deeper learning, rather than just a quick check, you’ll strengthen your problem-solving skills and build a stronger foundation for future challenges.
Step-by-Step Problem Solving Techniques
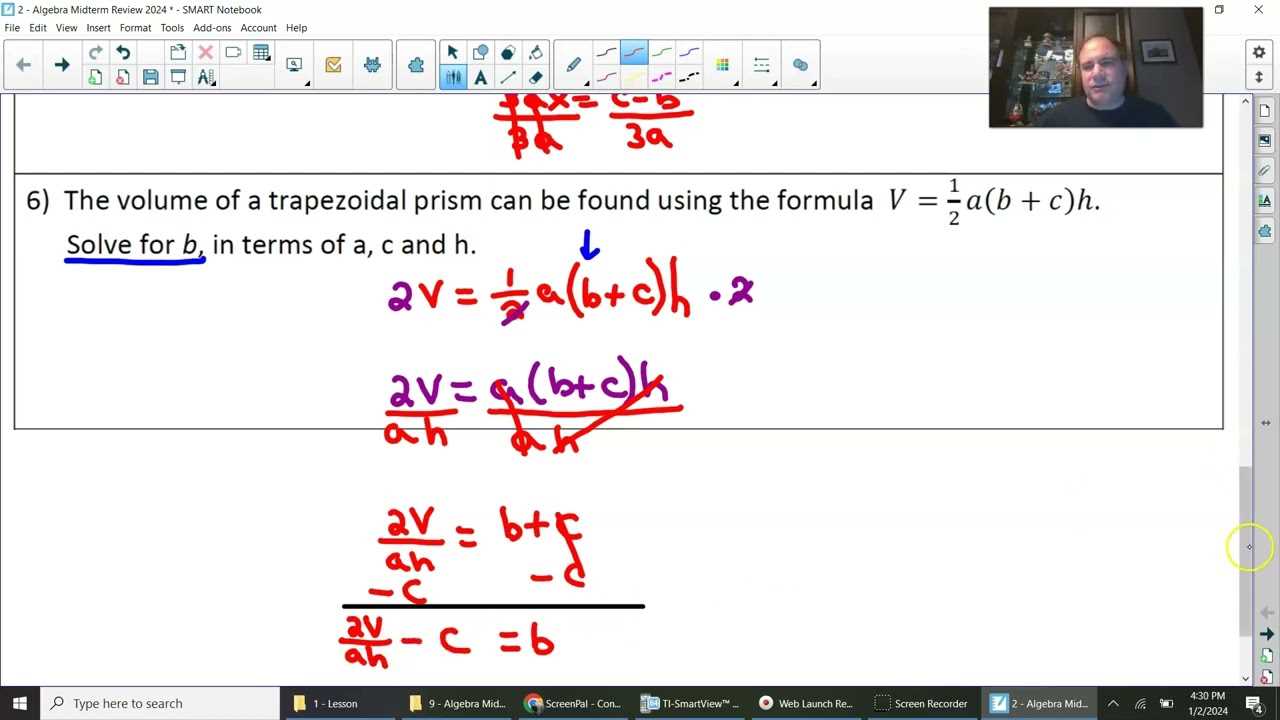
Approaching complex challenges in mathematics requires a methodical strategy to break down each problem into smaller, manageable parts. By following a clear, step-by-step process, you can ensure that every element is addressed and nothing is overlooked. This structured approach not only helps avoid mistakes but also makes it easier to understand the reasoning behind each solution.
The first step is to carefully read the problem and identify what is being asked. Understanding the question is crucial before attempting any calculations. Once you have a clear idea of what is required, outline the known information and the variables involved.
Next, determine which mathematical operations or techniques are needed to proceed. This could involve simplifying expressions, applying formulas, or rearranging terms. Break down the problem further by applying these methods step by step, ensuring each calculation is correct before moving to the next stage.
Finally, once you have reached a solution, double-check your work. Ensure that the result makes sense in the context of the problem and that all steps align logically. This final review helps to catch any errors that may have occurred during the process.
Best Practices for Midterm Exam Preparation
Preparing for a significant test involves more than just reviewing material at the last minute. To truly succeed, it’s essential to adopt effective strategies that allow you to learn and retain information efficiently. By establishing a clear study plan, focusing on key topics, and practicing regularly, you can approach the assessment with confidence and clarity.
Here are some best practices to follow as you prepare:
- Start early: Begin your preparation well ahead of the test date. This allows you to pace yourself and avoid cramming at the last moment, which can lead to stress and confusion.
- Prioritize difficult topics: Identify areas where you struggle the most and spend extra time reinforcing your understanding. These are often the sections where you’ll need the most practice and attention.
- Practice regularly: Regular practice is key to mastering concepts. Work through a variety of problems to reinforce your skills and improve your speed.
- Review past problems: Going through previous tests, quizzes, or practice problems helps familiarize you with the types of questions that may appear and the methods used to solve them.
- Use active learning techniques: Rather than simply reading over notes, engage actively by solving problems, explaining concepts out loud, or teaching them to someone else.
- Take breaks: Studying for long hours without breaks can lead to burnout. Short breaks throughout your study sessions will help maintain focus and improve retention.
- Get plenty of rest: A well-rested mind performs better. Ensure you get enough sleep the night before the test to stay sharp and focused.
By following these techniques, you can build a solid foundation of knowledge and feel more prepared and confident on the day of the test.
Breaking Down Complex Algebra Problems
When faced with a challenging mathematical problem, it can be overwhelming to know where to begin. The key to solving complex issues lies in breaking them down into simpler, more manageable steps. By analyzing each part of the problem methodically, you can find solutions with greater ease and accuracy. This approach helps reduce confusion and ensures a logical path to the answer.
Here’s a step-by-step approach to tackle difficult problems:
- Identify the main goal: Determine exactly what the problem is asking you to find. Understanding the desired outcome is crucial before starting any calculations.
- Highlight known information: List all the given values and expressions. This will serve as your foundation for solving the problem.
- Break it into parts: Divide the problem into smaller sections. Focus on solving one part at a time, whether it’s simplifying an expression or solving for a variable.
- Use appropriate formulas or methods: Depending on the type of problem, apply the necessary techniques such as factoring, substitution, or simplification to move forward.
- Check intermediate steps: After each calculation, review your work to ensure it aligns with the expected results. Small errors can accumulate if not caught early.
By taking the time to approach complex problems in this structured way, you’ll build confidence in your ability to handle even the most difficult questions. Consistent practice will also help develop a deeper understanding of how to break down and solve a wide variety of challenges.
Tips for Improving Algebra Skills

Enhancing your mathematical abilities requires consistent effort and the right approach. Mastering the fundamentals and applying various strategies can help you develop a deeper understanding of problem-solving techniques. With regular practice and a focus on key concepts, you can strengthen your skills and boost your confidence when tackling complex challenges.
Here are several effective tips to improve your mathematical skills:
| Tip | Description |
|---|---|
| Practice regularly | Consistent practice is essential to solidifying your understanding and improving speed. Try solving problems daily to reinforce your knowledge. |
| Focus on understanding, not memorization | Rather than memorizing formulas, strive to understand the reasoning behind them. This will help you apply them more effectively in different situations. |
| Work on fundamentals | Mastering basic concepts, such as simplifying expressions and solving equations, provides a strong foundation for more advanced topics. |
| Use additional resources | Explore online tutorials, practice exercises, or study guides to gain a broader perspective and reinforce challenging areas. |
| Break down problems into smaller steps | When faced with a difficult problem, break it into smaller, more manageable parts. Solving each part step by step will make the process easier. |
By implementing these strategies, you will gradually build stronger skills and gain greater proficiency in mathematical problem-solving.
How to Approach Word Problems
Word problems can often seem daunting due to their complexity and the need to translate real-life situations into mathematical equations. However, with the right approach, these problems can be tackled effectively. Breaking down the problem into smaller, more manageable steps allows you to focus on key information and apply the correct methods to find the solution.
Start by carefully reading the problem to understand what is being asked. Identify the key details and numbers, and determine what information you need to find. Often, word problems will include extra, irrelevant details designed to test your ability to focus on the relevant facts.
Next, translate the word problem into a mathematical form. This may involve setting up variables for unknown values, forming equations, or determining relationships between different quantities. Be sure to choose the right mathematical operations to use based on what the problem requires, such as addition, subtraction, multiplication, or division.
After setting up your equation or expression, solve the problem step by step. Ensure that each calculation is accurate, and check your work as you go. Once you’ve reached a solution, reread the problem to make sure your answer makes sense in the context of the situation described.
By following these steps, word problems become much more manageable, and you can approach them with confidence and clarity.
Reviewing Algebraic Functions and Equations
Understanding the relationship between variables and how they interact in mathematical expressions is crucial for solving problems efficiently. Functions and equations are foundational concepts that allow us to describe and analyze these relationships. Being comfortable with these concepts is essential for tackling more complex mathematical challenges and problem-solving scenarios.
The first step in mastering these concepts is to understand the structure of a function. Functions represent relationships where each input has a corresponding output, often denoted as f(x) or similar. Equations, on the other hand, show how two expressions are equal to one another, and solving them involves finding the value of the unknown variable.
Key Concepts in Functions

Functions are often represented in various forms such as graphs, tables, or equations. To understand them better, consider the following:
- Domain and Range: The domain refers to all possible input values, while the range represents the corresponding output values.
- Linear vs. Non-linear: Linear functions show a constant rate of change, whereas non-linear functions can have varying rates of change.
- Graph Interpretation: The graph of a function provides a visual representation of how the input and output are related.
Solving Equations
Equations are fundamental to problem-solving in mathematics. To solve equations, follow these general steps:
- Isolate the variable: Manipulate the equation to get the unknown variable on one side, while the constants or known terms are on the other side.
- Simplify: Combine like terms, eliminate parentheses, and perform arithmetic operations to simplify the equation.
- Check your solution: After solving for the variable, substitute it back into the original equation to ensure that it satisfies the equality.
Mastering both functions and equations will enhance your ability to solve a wide range of mathematical problems. With practice, these concepts will become intuitive and easier to work with in more complex scenarios.
Analyzing Solutions from the Answer Key
Once you’ve completed a set of problems, reviewing the solutions can offer invaluable insight into your understanding and problem-solving approach. Carefully analyzing the steps and reasoning behind each solution helps you identify any mistakes, clarify your thought process, and reinforce correct methods. This reflective practice enables you to improve and refine your skills for future challenges.
Start by closely examining the given solution. Look at the methods used to reach the final result and compare them to the steps you took. Ask yourself the following questions:
- Did I use the correct approach? Consider whether the method used in the solution matches the approach you used or if there is a more efficient way to solve the problem.
- Were all calculations accurate? Verify each step to ensure no arithmetic or logical errors were made during the solution process.
- Is the final result reasonable? Does the outcome make sense in the context of the problem? If not, identify where the discrepancy may have occurred.
By breaking down each solution, you can recognize patterns and common strategies that lead to success. With each review, your ability to solve problems with greater accuracy and efficiency will improve.
Additionally, consider these steps to further enhance your understanding:
- Identify the key concepts: Determine which mathematical concepts were most important in solving the problem and ensure you fully grasp them.
- Practice similar problems: Once you’ve understood the solution, practice more problems of the same type to reinforce the learned techniques.
- Seek clarification on mistakes: If any errors occurred, review the specific part where the mistake was made and work through it again to understand the correction.
By consistently analyzing solutions, you’ll gain greater confidence in your problem-solving abilities and be better equipped to tackle more complex scenarios in the future.
Test-Taking Strategies for Algebra Exams
Effective strategies during an assessment can significantly influence your performance. Knowing how to approach the test, manage your time, and handle various types of problems is key to achieving success. A solid test-taking strategy not only helps you stay organized but also allows you to approach each question with confidence and clarity.
To maximize your performance, consider the following methods:
| Strategy | Description |
|---|---|
| Skim Through the Entire Test | Before starting, quickly read through all the questions to understand the overall structure and identify the sections that may take more time. |
| Start with Easier Questions | Begin with the questions you find easiest. This builds confidence and ensures you score points early. |
| Time Management | Allocate a specific amount of time for each section. Keep track of time to ensure you don’t spend too long on one question. |
| Show Your Work | Write out all your steps clearly, even for simple calculations. This not only helps in case of mistakes but also may earn partial credit. |
| Double-Check Your Answers | If time permits, review your answers to correct any potential errors or oversights. |
By incorporating these strategies into your test-taking routine, you will enhance your ability to manage time, reduce anxiety, and approach each question with a clear, systematic approach. These habits will serve you well in any mathematical challenge you encounter.
Understanding Algebraic Formulas and Rules
Grasping the essential formulas and rules in mathematics is crucial for solving problems efficiently and accurately. These principles serve as the foundation for understanding how numbers and variables interact in equations. By mastering these fundamental concepts, you can approach more complex problems with greater confidence and skill.
One of the most important aspects of working with mathematical relationships is recognizing the structure of different formulas. Each formula has its specific application and is designed to simplify the problem-solving process. Familiarizing yourself with these relationships helps you identify which tools to use when faced with various types of problems.
Additionally, understanding the rules governing mathematical operations is equally important. These rules guide how operations such as addition, subtraction, multiplication, and division are applied within equations. Adhering to these guidelines ensures consistency and accuracy when manipulating mathematical expressions.
Key strategies to better understand these concepts include:
- Practice frequently: Repeated practice with various formulas helps solidify your understanding and improves recall during problem-solving.
- Identify patterns: Look for common patterns across different problems that allow you to apply similar strategies or formulas.
- Break down complex problems: When dealing with more complicated scenarios, break the problem into smaller, more manageable parts and apply the appropriate formula step-by-step.
By mastering these formulas and rules, you’ll build a stronger mathematical foundation, making it easier to approach and solve a wide range of problems with precision and confidence.
Common Algebra 1 Topics on Midterms

When preparing for a key assessment in mathematics, it’s essential to familiarize yourself with the most frequently tested concepts. These topics form the backbone of many problems, and understanding them thoroughly is crucial to performing well. This section highlights several of the core areas that students often encounter, providing insights on how to approach and tackle them effectively.
Linear Equations and Inequalities

One of the fundamental concepts tested involves solving equations and inequalities that involve variables. Mastery in balancing both sides of an equation, isolating variables, and applying rules to inequalities is essential. Common techniques include:
- Identifying coefficients and constants
- Using inverse operations to solve
- Graphing inequalities on number lines
Systems of Equations
Another critical topic is solving systems of equations. Whether through substitution, elimination, or graphing, solving these systems requires a solid understanding of how to manipulate multiple equations simultaneously. Key steps to focus on include:
- Substituting one equation into another
- Eliminating variables through addition or subtraction
- Graphing and finding intersection points
By focusing on these areas and practicing the various techniques associated with them, students can improve their problem-solving abilities and gain greater confidence in tackling complex tasks. Strong knowledge of these concepts often forms the basis for success in various questions.
How to Self-Assess Your Progress
Tracking your progress in mathematics is an important step towards improvement. Self-assessment allows you to identify strengths and areas that need more attention. By evaluating your understanding of key concepts and problem-solving strategies, you can tailor your study routine and focus on areas where you need the most practice. This section outlines practical methods for self-assessing your abilities effectively.
Identify Key Areas of Strength
The first step in self-assessment is to recognize which topics you are comfortable with. These are the areas where you can solve problems with confidence and minimal assistance. Reflecting on past work can help you identify these areas. Consider the following:
- What types of problems do you complete without much effort?
- Which concepts do you grasp quickly during practice or study sessions?
- Are there any topics where you consistently perform well in assignments or tests?
Recognize Areas Needing Improvement
Equally important is identifying areas where you struggle. This can help guide your focus during study sessions. Reflect on past mistakes and challenging questions to pinpoint where you need more practice. To help guide this process, consider the following:
- Which problems do you find time-consuming or difficult to complete?
- Are there recurring mistakes or patterns in your solutions?
- Do you require extra help or resources to understand certain concepts?
Using Practice Tests for Assessment
One effective way to evaluate your progress is through practice assessments. They help simulate the actual testing environment and reveal your level of readiness. While completing a practice test, take note of:
- Your ability to manage time and complete the questions efficiently
- The accuracy of your solutions
- The types of questions that challenge you most
Tracking Progress Over Time
Consistent self-assessment helps you track your improvement. Regularly reflect on your past performance, compare results, and adjust your study methods as necessary. Keeping a log or journal of your self-assessments can help you monitor progress and build a plan for further improvement. Consider creating a table to track your performance across various topics:
| Topic | Confidence Level (1-5) | Areas Needing Improvement | Action Plan |
|---|---|---|---|
| Linear Equations | 4 | Solving complex multi-step equations | Practice more problems and review key steps |
| Systems of Equations | 3 | Substitution method | Watch tutorials and solve additional problems |
| Polynomials | 2 | Factoring and simplifying | Seek help from a tutor and complete targeted exercises |
By consistently assessing your progress and focusing on areas that need improvement, you can steadily enhance your understanding and skills. This will help you build confidence and approach each topic with a clearer, more focused mindset.
What to Do After the Midterm
Once the testing period is over, it’s essential to reflect on the process and use the feedback to improve for future assessments. Whether the outcome was positive or there are areas needing further work, the time after the test is an opportunity to solidify your understanding and adjust your approach. Below are steps you can take to make the most of the post-test period.
Analyze Your Performance
Start by reviewing your results to understand where you did well and where you struggled. This will help you gain clarity on which topics need more attention moving forward. Pay attention to the following:
- Identify questions you missed and review the solutions to understand your errors.
- Note patterns in mistakes, such as misunderstandings of specific concepts or recurring errors in calculations.
- Assess if time management affected your performance, particularly if you couldn’t finish the test.
Use Mistakes as Learning Opportunities
Instead of focusing on what went wrong, use mistakes as a valuable tool for growth. Each error highlights a concept or technique that needs more practice. To address these, consider the following:
- Revisit the concepts you struggled with and go over practice problems.
- Seek additional resources such as videos, guides, or a tutor to reinforce weak areas.
- Make sure to work on similar problems to build confidence and avoid repeating the same mistakes.
Adjust Your Study Habits
After evaluating your performance, consider whether your current study techniques were effective. It may be time to tweak your approach to better align with your goals. Here are some suggestions:
- Implement a more consistent study schedule leading up to the next test.
- Focus on active learning methods such as solving problems, explaining concepts aloud, or creating flashcards.
- Set small, measurable goals for each study session to keep track of progress.
By taking the time to reflect, adjust, and plan for the future, you can turn any experience into a stepping stone towards greater understanding and success in your studies.
Resources for Further Practice
After completing your assessments, it’s important to continue refining your skills and reinforcing concepts. There are numerous tools and platforms that provide opportunities for extra practice and deeper understanding. Whether you’re looking for structured lessons or interactive exercises, these resources will help you strengthen your grasp on essential topics.
Online Platforms and Websites
Several websites offer free exercises and tutorials, catering to different learning styles. Here are a few to consider:
- Khan Academy – Provides video lessons and practice problems across various topics.
- IXL – Offers interactive exercises with instant feedback and progress tracking.
- Mathway – A problem solver that explains step-by-step solutions to help understand how to approach different types of questions.
Books and Workbooks

Many textbooks and workbooks offer exercises with solutions and explanations, making them a great way to practice. Some popular options include:
- “The Practice of Mathematics” – A workbook that covers a wide range of topics and provides detailed answers to help understand each concept.
- “Algebra: A Combined Approach” – This textbook offers thorough explanations and exercises designed to improve problem-solving skills.
Study Groups and Peer Collaboration
Sometimes, collaborating with others can provide different perspectives on challenging topics. Joining a study group or finding a study buddy can help with:
- Discussing difficult problems and solutions together.
- Sharing tips and techniques for better understanding.
- Receiving feedback and constructive criticism on your approach to solving problems.
Utilizing a combination of these resources will enhance your understanding and ensure continuous improvement as you build confidence and mastery in mathematical problem solving.