
When preparing for a crucial assessment in mathematics, it’s important to understand the core principles that will help you solve complex problems quickly and accurately. Achieving proficiency in this area requires not only knowledge of the concepts but also the ability to apply them effectively under pressure.
Through detailed solutions and clear methodologies, you can strengthen your problem-solving skills and increase your confidence. Breaking down challenging questions into manageable steps ensures you can tackle any scenario with ease. Reviewing common techniques and strategies is key to refining your approach.
In this guide, we will walk through various examples and solutions, providing you with valuable insights into the problem-solving process. With this knowledge, you’ll be ready to approach your assessment with clarity and precision.
Comprehensive Mathematical Solutions Guide
Mastering the principles of applied mathematics requires a strategic approach to solving problems. Understanding the logic behind equations and being able to break them down into smaller, more manageable steps is essential for achieving success. With clear guidance, anyone can learn to navigate through complex calculations with confidence and accuracy.
This guide provides a thorough breakdown of various mathematical problems commonly encountered in assessments. Each example is explained step by step, highlighting the key techniques that will help you approach any question systematically. Whether dealing with percentages, ratios, or more advanced calculations, the focus is on building a strong foundation in problem-solving.
By practicing with real-world examples, you can develop an intuitive understanding of how to apply these principles. Focused practice ensures that you can confidently handle similar problems, while understanding the core concepts helps you adapt your approach to any situation that may arise.
Understanding Key Assessment Concepts

To excel in any mathematical assessment, it is crucial to grasp the underlying concepts that drive problem-solving. Having a solid understanding of the principles behind the questions will help you approach them confidently and effectively. By breaking down each type of problem into its basic components, you can identify the most efficient strategies for finding the correct solution.
Focusing on core areas such as operations with numbers, understanding relationships between variables, and interpreting word problems can significantly improve performance. Recognizing how these elements connect to form more complex scenarios will give you the flexibility to tackle any challenge presented in the test.
By revisiting fundamental topics and practicing their application in various forms, you will develop the skills needed to navigate through the questions with ease. A clear grasp of the basic rules and methods ensures that you can quickly recognize the best approach in any situation.
Essential Topics for Assessment Success
To perform well in any mathematics assessment, it is crucial to focus on the fundamental areas that form the core of most questions. A deep understanding of these key topics not only improves your ability to solve problems but also boosts your confidence in handling a variety of challenges. By mastering these concepts, you can navigate through the test more effectively and efficiently.
Core Concepts to Master
Familiarity with the following areas is vital for success:
| Topic | Description | Importance |
|---|---|---|
| Linear Equations | Understanding how to solve for unknowns in straight-line relationships. | Essential for solving many types of problems. |
| Interest and Percentage | Calculating rates, percentages, and interest over time. | Frequently encountered in real-life application problems. |
| Functions and Graphs | Interpreting and plotting mathematical relationships. | Critical for visualizing and solving complex scenarios. |
| Exponential Growth | Working with scenarios where values grow at an increasing rate. | Important for finance and population models. |
How to Approach These Topics
Approach each of these topics with a focus on practice. Begin by reviewing the basic concepts and then move to more complex applications. Understanding the theoretical underpinnings allows you to solve problems faster and more accurately during the assessment.
Step-by-Step Problem Solving Techniques
Effective problem solving in mathematics requires a structured approach that helps break down complex challenges into manageable steps. By following a systematic method, you can tackle even the most difficult problems with clarity and confidence. The key is to understand the process and apply it consistently to each problem type.
Below are the essential steps to follow when solving a mathematical problem:
| Step | Action | Purpose |
|---|---|---|
| 1 | Understand the Problem | Read carefully to identify what is being asked and what information is given. |
| 2 | Organize Information | List known values and variables, and note any relevant formulas. |
| 3 | Set Up an Equation | Translate the problem into a mathematical equation or expression. |
| 4 | Solve the Equation | Perform the necessary operations to isolate the unknown variable. |
| 5 | Check the Solution | Substitute the solution back into the original equation to verify its accuracy. |
By practicing these steps, you will improve your ability to approach any problem logically and methodically. This approach minimizes errors and helps ensure that you arrive at the correct solution.
Reviewing Common Mathematical Formulas
Having a solid understanding of key formulas is essential for solving a wide range of problems efficiently. These formulas serve as tools that simplify complex calculations and help you solve for unknown variables. Mastering the most common equations and recognizing when to apply them can save valuable time during assessments and real-world applications.
Basic Operations and Relationships

Understanding basic formulas is the foundation of problem-solving. These formulas allow you to handle simple to moderate problems with ease. Some important relationships to remember include:
- Linear Equations: y = mx + b – Defines the relationship between two variables in a straight line.
- Quadratic Equations: ax² + bx + c = 0 – A second-degree equation often used in curve fitting and other complex calculations.
- Percentage Calculations: Percentage = (Part/Whole) × 100 – Used for finding portions of a total.
Advanced Formulas for Specific Applications
Once you are familiar with basic formulas, it’s important to dive into more specialized ones that can be applied to specific types of problems. Some of these include:
- Compound Interest Formula: A = P(1 + r/n)^(nt) – Used to calculate the accumulated amount of an investment over time with interest.
- Exponential Growth: y = y₀e^(kt) – Describes how quantities grow over time at a constant rate.
- Distance Formula: d = √[(x₂ – x₁)² + (y₂ – y₁)²] – Used for calculating the distance between two points in a coordinate plane.
By reviewing these formulas and understanding their application, you can quickly identify the right approach to a problem and solve it with precision.
Tips for Efficient Time Management
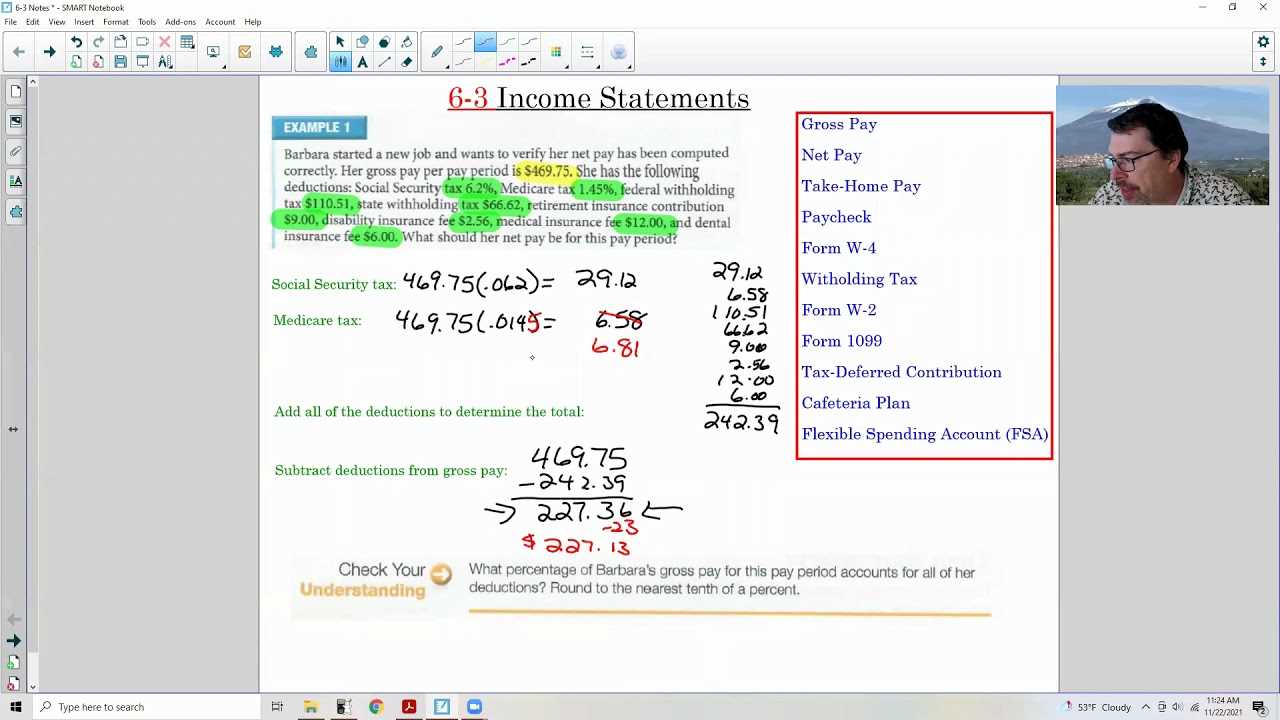
Effective time management is crucial when tackling any assessment. Being able to allocate your time wisely allows you to complete tasks more efficiently, reducing stress and increasing accuracy. By planning ahead and staying organized, you can make the most of the time available and ensure you cover all the necessary material.
Here are some tips to help you manage your time more effectively during an assessment:
- Prioritize Tasks: Focus on problems that are worth the most points or those that you find most challenging. This ensures that you don’t spend too much time on easier questions at the expense of harder ones.
- Set Time Limits: Allocate a set amount of time to each section or question. Stick to these limits to avoid spending too long on any one part of the test.
- Skip and Return: If you encounter a difficult problem, move on and come back to it later. This allows you to maintain momentum and prevents frustration from slowing you down.
- Break Tasks into Smaller Steps: When faced with a complex problem, break it down into manageable parts. Solving smaller components one at a time will help keep you on track.
- Practice Under Timed Conditions: Simulating real-time conditions during your study sessions helps you get used to managing your time effectively during the actual assessment.
By implementing these strategies, you can stay focused and make the most of the time available to you, ensuring that you approach each problem with the attention it deserves.
How to Tackle Word Problems Effectively
Word problems often pose a unique challenge, as they require not only mathematical skills but also the ability to interpret real-world scenarios. The key to solving these problems is to break them down into smaller, more manageable pieces. By following a clear process, you can avoid feeling overwhelmed and focus on finding the solution.
Step-by-Step Approach

When faced with a word problem, follow these steps to guide your solution:
- Read the Problem Carefully: Make sure you understand what is being asked. Identify the key information provided and take note of the question that needs to be answered.
- Identify Relevant Information: Extract the data you need to solve the problem. This may include numbers, relationships, and conditions mentioned in the text.
- Define Variables: Assign variables to represent unknown quantities. This will make it easier to set up equations or expressions later on.
- Translate Words into Math: Convert the text into mathematical expressions or equations. Look for keywords that indicate operations, such as “sum,” “difference,” “product,” or “quotient.”
- Solve and Interpret: Solve the equation and interpret the results in the context of the problem. Ensure that your solution answers the specific question asked.
Common Pitfalls to Avoid
There are a few common mistakes to be aware of when tackling word problems:
- Ignoring Units: Always pay attention to the units of measurement (e.g., dollars, hours, meters). Ensure that all units are consistent throughout the problem.
- Overlooking Key Information: Sometimes, extra details are included to mislead you. Stay focused on the information directly related to the problem.
- Skipping Steps: It’s easy to rush through word problems, but skipping steps can lead to errors. Make sure to work through each part systematically.
By following a structured approach and avoiding common mistakes, you can tackle word problems with confidence and accuracy.
Breaking Down Complex Equations
When dealing with complex mathematical expressions, it’s important to approach them step by step. Breaking down each part of the equation helps simplify the process, making it easier to identify solutions. By following a systematic method, even the most intricate problems can be tackled with confidence.
Approach to Simplification
To effectively simplify complex equations, follow these general steps:
- Identify the Structure: Start by analyzing the equation’s structure. Look for terms that can be combined or simplified, such as like terms or common factors.
- Apply the Order of Operations: Use the order of operations (PEMDAS) to guide your calculations. This ensures that you simplify the equation correctly and avoid making mistakes.
- Isolate Variables: Try to isolate the variable you are solving for. This often involves moving terms from one side of the equation to the other using addition, subtraction, multiplication, or division.
- Simplify Step by Step: Take it one step at a time. Simplifying large expressions in smaller, more manageable parts will help prevent confusion and errors.
- Check for Factoring: If the equation involves polynomials, check if factoring can simplify the process. Factoring is often a useful technique to reduce complex expressions.
Common Techniques for Solving
Here are some common methods to solve more complex equations:
- Substitution: Use substitution to replace one expression with a simpler one, especially when you have multiple variables or equations.
- Elimination: This method is often used for systems of equations. By adding or subtracting equations, you can eliminate one variable, making it easier to solve for the others.
- Quadratic Formula: For equations involving squares, the quadratic formula can be used to find the solutions directly, without needing to factor.
- Graphical Solutions: In some cases, graphing an equation can help visualize the solutions, especially when dealing with linear or quadratic equations.
Breaking down complex equations into smaller, simpler steps helps you avoid errors and makes solving much more manageable. By practicing these techniques, you will improve your ability to handle even the most challenging problems with ease.
Real-Life Applications of Financial Algebra

Mathematical concepts are not just confined to the classroom; they have real-world applications that impact our daily lives. By understanding how to solve problems involving numbers, rates, and variables, we can make informed decisions about finances, investments, and planning. These skills are useful for everything from budgeting personal expenses to analyzing business growth.
Personal Finance Management
One of the most common applications is in personal finance, where mathematical skills are crucial for managing income and expenses. Here are a few ways in which these concepts are applied:
- Budgeting: Understanding how to allocate funds to different categories such as housing, utilities, and savings requires the ability to work with percentages, averages, and ratios.
- Loans and Interest Rates: When taking out a loan, understanding how interest accumulates over time is essential. Whether it’s a mortgage or a car loan, knowing how to calculate total costs and repayment schedules helps in making smarter financial choices.
- Investment Analysis: Knowing how to calculate return on investment (ROI) or assess stock performance requires the application of mathematical formulas to determine profitability.
Business and Economics
In business and economics, mathematical skills are used to optimize operations, plan for future growth, and make informed decisions about resources. Some key areas where these skills are applied include:
- Cost-Price Analysis: Businesses use mathematical models to determine pricing strategies, ensuring they cover costs while remaining competitive in the market.
- Profit and Loss Projections: Projecting future profits or losses based on current financial data involves the use of formulas to calculate expected outcomes, helping businesses plan for expansion or cost-cutting measures.
- Market Research: Mathematical analysis of market trends, consumer behavior, and sales forecasts helps companies determine product demand and pricing strategies.
By applying mathematical concepts to everyday financial situations, individuals and businesses can make better-informed decisions, leading to improved financial health and long-term success.
Common Mistakes to Avoid on the Exam

While preparing for any assessment, it’s easy to fall into certain traps that can lead to avoidable errors. Understanding where students typically make mistakes can help you stay vigilant and improve your accuracy during the test. By being aware of common pitfalls, you can enhance your ability to work through problems efficiently and effectively.
Here are some of the most frequent mistakes to avoid during your preparation and on the actual assessment:
- Misinterpreting the Problem: One of the most common errors is misunderstanding the problem’s requirements. Always read the question carefully and make sure you understand what is being asked before starting the solution.
- Skipping Steps: Rushing through problems often leads to missed steps. Take the time to write out each step in your solution process. This helps ensure accuracy and makes it easier to check your work.
- Forgetting Units or Conversions: Whether it’s measurements or currency, neglecting to track units or convert them properly can throw off your entire calculation. Always double-check that your units align correctly across the problem.
- Overcomplicating the Solution: Sometimes, students try to apply overly complex methods when simpler approaches will suffice. Look for ways to simplify the problem by breaking it into smaller parts or using basic operations to solve it.
- Not Reviewing Your Work: Failing to review your answers can lead to small mistakes that could have been easily spotted. If time allows, always go back and verify your calculations before submitting your work.
Avoiding these common errors can significantly improve your performance and reduce stress during assessments. With careful attention to detail and a solid understanding of the material, you can approach the test with confidence and accuracy.
How to Interpret Financial Statements
Understanding and interpreting financial statements is crucial for making informed decisions in business and personal finances. These documents provide a snapshot of an entity’s financial health, detailing everything from income and expenses to assets and liabilities. By analyzing them, you can gain insight into the performance, profitability, and sustainability of a business or investment.
Key Components of Financial Statements
There are several key components that make up a typical financial statement. Each provides a different aspect of the financial picture:
- Income Statement: This document outlines revenues, expenses, and profits over a specific period. It shows whether the entity is operating at a profit or a loss, helping to evaluate overall performance.
- Balance Sheet: The balance sheet lists assets, liabilities, and equity. It provides a snapshot of what the company owns and owes at a particular point in time.
- Cash Flow Statement: This statement tracks the inflow and outflow of cash, providing insight into the liquidity and financial flexibility of the entity.
How to Analyze Key Metrics
When interpreting financial statements, certain ratios and metrics can help you assess the overall financial situation:
- Profitability Ratios: These ratios, such as the net profit margin, give insight into how efficiently a company generates profit relative to its revenue.
- Liquidity Ratios: Ratios like the current ratio measure the ability of a business to meet its short-term obligations, giving an indication of financial stability.
- Solvency Ratios: These ratios assess the long-term financial health of a business by analyzing its ability to meet long-term debt obligations.
By examining these components and metrics, you can get a clear understanding of a business’s financial standing and make informed decisions regarding investments, loans, or financial planning.
Solving Linear and Quadratic Equations
Solving equations is a fundamental skill in mathematics that allows you to find the value of an unknown variable. There are two common types of equations that students often encounter: linear and quadratic equations. Each type follows its own set of rules for solving, but the underlying principle remains the same–manipulate the equation to isolate the variable on one side.
Solving Linear Equations
A linear equation involves variables raised to the first power, and its solution represents a straight line when graphed. The goal is to isolate the variable by using basic operations like addition, subtraction, multiplication, and division.
- Step 1: Simplify both sides of the equation.
- Step 2: Move all terms with the variable to one side of the equation and constant terms to the other.
- Step 3: Solve for the variable by performing the necessary operations.
- Step 4: Check the solution by substituting it back into the original equation.
Solving Quadratic Equations
Quadratic equations involve terms where the variable is squared (raised to the second power). These equations can be solved using several methods, including factoring, completing the square, and the quadratic formula.
- Factoring: Express the quadratic equation as a product of two binomials and solve for the variable.
- Completing the Square: Rearrange the equation into a perfect square trinomial and solve for the variable.
- Quadratic Formula: Apply the quadratic formula, x = (-b ± √(b² – 4ac)) / 2a, where a, b, and c are the coefficients of the quadratic equation.
By mastering these techniques, you can solve both linear and quadratic equations confidently, improving your problem-solving skills in various mathematical contexts.
Mastering Interest and Discount Calculations
Understanding how to calculate interest and apply discounts is an essential skill in both personal finance and business. These concepts are often used to determine how much money you will earn or pay over time, or how much a product will cost after a reduction. By mastering these calculations, you can make better financial decisions and optimize savings or investments.
Calculating Simple and Compound Interest
Interest is the amount paid for the use of money, and it can be calculated in different ways. The two most common methods are simple interest and compound interest. Simple interest is calculated on the principal amount only, while compound interest takes into account both the principal and the interest accumulated over time.
- Simple Interest Formula: I = P × r × t, where P is the principal, r is the interest rate, and t is the time period.
- Compound Interest Formula: A = P × (1 + r/n)^(nt), where P is the principal, r is the interest rate, n is the number of times interest is compounded per year, and t is the time in years.
Understanding Discounts and Markups
Discounts are reductions in the original price of a product or service, while markups refer to the increase in the price over the cost of goods sold. Understanding how to apply these can help you calculate final sale prices or profit margins accurately.
- Discount Calculation: Discounted Price = Original Price × (1 – Discount Rate)
- Markup Calculation: Sale Price = Cost × (1 + Markup Rate)
By applying these formulas, you can easily determine the effects of interest and discounts, helping you plan your finances or assess product prices with confidence.
Preparing for Word Problems in Mathematics
Word problems in mathematics often present real-world scenarios where you must identify the key information and apply the appropriate formulas to find a solution. These problems test your ability to translate abstract concepts into practical situations. Preparing for them requires both a solid understanding of mathematical principles and the ability to break down complex information into manageable parts.
When tackling word problems, it’s important to first read through the problem carefully. Look for keywords and phrases that indicate the type of operation needed, such as “total,” “increase,” “decrease,” or “difference.” Identifying these clues helps you determine which mathematical approach is required.
Next, organize the given information by writing it down clearly. This allows you to visualize the relationships between different elements in the problem, making it easier to apply the correct equations. Lastly, solve the problem step-by-step, checking your work as you go to ensure accuracy.
With practice, you can develop a systematic approach to solving word problems, which will help you tackle them more efficiently and effectively.
Using Graphs to Solve Mathematical Problems
Graphs are powerful tools for visually representing relationships between variables, making it easier to understand and solve complex mathematical problems. By plotting equations on a coordinate plane, you can gain insights into the behavior of functions, identify solutions, and analyze trends. Using graphs allows you to translate abstract numerical problems into more tangible visual forms, which can simplify the process of finding solutions.
In many cases, graphical methods provide an intuitive approach to solving problems that may seem overwhelming when approached algebraically. For instance, finding the point where two functions intersect is straightforward when you can see the graphs on the same grid. The intersection point represents the solution to the system of equations, providing a clear visual answer.
How to Use Graphs Effectively
- Plot Key Points: Before drawing the entire graph, plot key points that represent the equation’s behavior. This helps you understand its overall shape and location on the coordinate plane.
- Look for Intersections: The point where two graphs meet is often the solution to a system of equations or the point of interest for the problem.
- Analyze the Slope: The slope of a line gives you important information about how one variable changes in relation to another. Pay attention to the slope to understand the rate of change.
Example of Using Graphs
| Equation | Graph Behavior | Solution |
|---|---|---|
| y = 2x + 3 | A straight line with a slope of 2 and a y-intercept of 3. | Identifying the point where this line intersects another function or line gives the solution. |
| y = -x + 1 | A straight line with a slope of -1 and a y-intercept of 1. | By plotting both lines, the intersection point provides the solution to the system of equations. |
By mastering the use of graphs, you can approach mathematical problems from a new perspective, simplifying what would otherwise be more challenging calculations. Understanding the visual representation of mathematical relationships is an essential skill for solving complex equations and interpreting data effectively.
Boosting Your Confidence Before the Test
Approaching a test can be a daunting experience, but with the right strategies, you can boost your confidence and face the challenge with a positive mindset. Confidence plays a crucial role in performing well, as it allows you to approach problems with clarity and focus. Preparing effectively and adopting the right mental approach can make all the difference when it comes to handling tough questions.
One of the key ways to build confidence is through consistent preparation. Knowing that you have dedicated time to study and practice can alleviate anxiety and help you feel more in control. In addition to studying the material, it’s also important to take care of your mental and physical well-being leading up to the test. A balanced approach can ensure that you are mentally sharp and ready for the task at hand.
Tips for Building Confidence
- Review Key Concepts: Focus on the topics that you find most challenging, and break them down into smaller, more manageable parts. This will help you feel more in control.
- Practice with Sample Problems: The more you practice solving problems similar to those you might encounter, the more comfortable you’ll feel during the test.
- Stay Positive: Replace negative thoughts with positive affirmations. Remind yourself of your preparation and the hard work you’ve put in.
- Take Breaks: Don’t overwhelm yourself by studying for long periods without rest. Taking short breaks can help you maintain focus and reduce stress.
- Visualize Success: Imagine yourself succeeding on the test. Visualizing a positive outcome can help reinforce a confident mindset.
Maintaining Calm on Test Day
- Arrive Early: Getting to the test location with plenty of time will allow you to settle in and avoid unnecessary stress.
- Manage Your Time: During the test, pace yourself and allocate enough time to address each question. Don’t spend too long on any one problem.
- Stay Focused: Keep your mind focused on the present moment, and avoid thinking too far ahead or worrying about questions you haven’t answered yet.
By integrating these strategies into your routine, you can increase your self-assurance and approach your test with a calm and positive outlook. Remember, confidence is built through preparation, self-belief, and a strategic mindset. The more you practice, the better equipped you will be to tackle any challenge that comes your way.