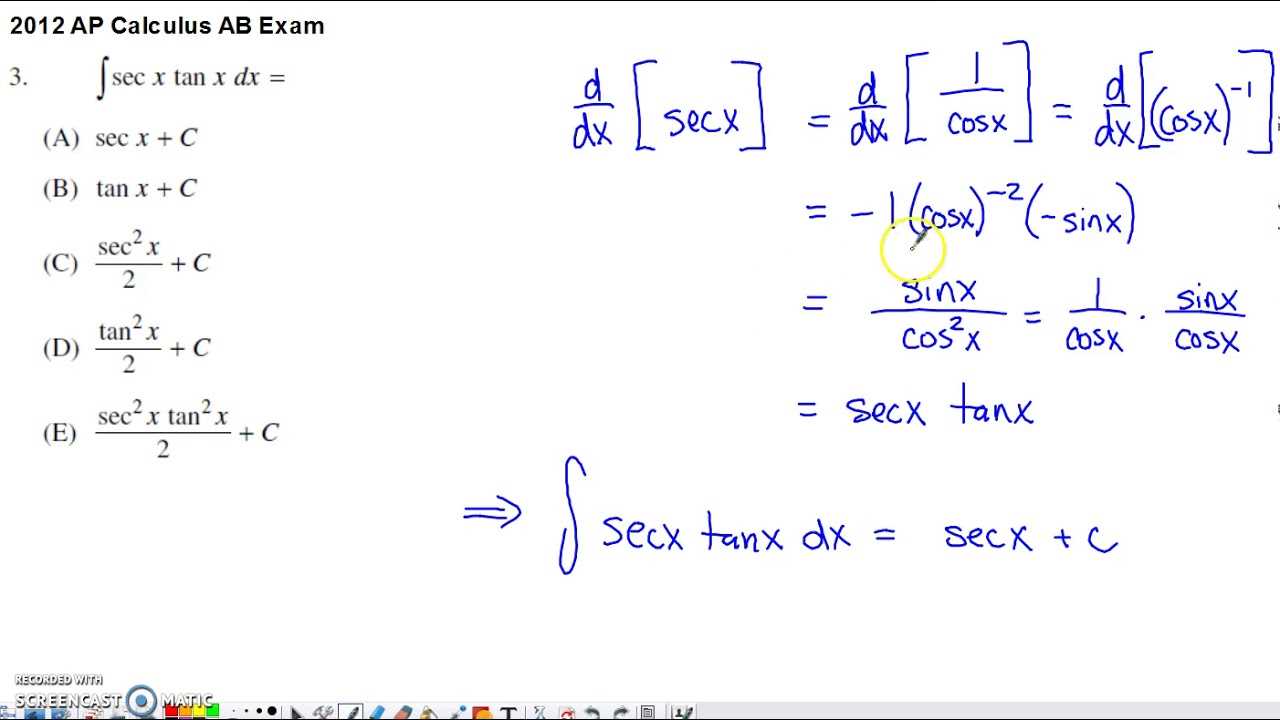
Approaching a crucial academic challenge requires not only knowledge but also the right strategies to perform well under pressure. This section focuses on preparing effectively for the upcoming test that evaluates your grasp of advanced mathematical concepts. It emphasizes the importance of a structured review process, alongside practical tips to navigate through the assessment confidently.
Mastering key principles and identifying areas for improvement are critical steps in maximizing your potential. With a thoughtful approach to practicing problems and understanding underlying concepts, you’ll be able to tackle the most complex sections of the test. This guide offers insights into typical question formats, strategies for success, and common pitfalls to avoid.
By preparing strategically, you can approach the challenge not just with readiness, but with the confidence that comes from thorough preparation. A strong foundation and methodical practice will ensure you’re equipped to demonstrate your knowledge efficiently and accurately.
AP Calculus AB Midterm Exam Overview
In this section, we provide an outline of the key components that you will encounter during the upcoming assessment. It is designed to evaluate your proficiency in a variety of advanced mathematical topics, testing both your problem-solving abilities and conceptual understanding. Preparation for this challenge involves understanding its structure and the types of questions you will face.
The assessment is divided into different sections, each focusing on specific areas of the subject matter. These sections are designed to test your ability to apply mathematical principles to solve complex problems under time constraints. A well-rounded approach to studying these topics will give you the flexibility to address a range of question formats, from theoretical inquiries to practical applications.
Knowing the structure and what to expect will help you approach each part of the assessment with clarity and confidence. Familiarity with the general flow and the types of tasks you will be required to perform ensures that you’re not just prepared for the content, but also ready for the format and pacing of the challenge.
Understanding the Exam Structure
To succeed in any significant assessment, it’s crucial to have a clear understanding of how the questions are organized and what is expected in each section. The structure of the upcoming test is divided into multiple parts, each serving a specific purpose in evaluating your mastery of the subject. Knowing the layout in advance will allow you to prepare more efficiently and confidently.
Multiple Choice Section
The first section consists of multiple-choice questions, which test your ability to quickly apply concepts to solve problems. These questions are typically designed to cover a broad range of topics, allowing you to demonstrate your knowledge and reasoning skills. Time management is key here, as the questions require both accuracy and speed.
Free Response Section
The second part features free-response questions that require more detailed, step-by-step solutions. In this section, you will need to show your full understanding of mathematical procedures, offering clear explanations and justifying each step of your work. This section is designed to evaluate your deeper comprehension and problem-solving abilities.
Key Topics Covered in AP Calculus AB
This section outlines the fundamental concepts and key areas that are typically evaluated during the assessment. A solid understanding of these topics is crucial for success, as they form the foundation for most questions. Each area focuses on different aspects of mathematical theory and application, testing both conceptual knowledge and problem-solving abilities.
The topics you will encounter are wide-ranging and cover various techniques and principles. Below are the core areas you should focus on during your preparation:
- Limits and Continuity – Understanding the behavior of functions as they approach specific points or infinity.
- Derivatives – Mastery of rate of change, slopes of curves, and optimization techniques.
- Integrals – Techniques for calculating areas under curves, as well as solving real-world problems involving accumulation.
- Fundamental Theorem of Calculus – The connection between differentiation and integration, and how to apply it.
- Applications of Derivatives – Exploring practical uses of derivatives in problems involving motion, rates, and tangents.
- Applications of Integrals – Using integration to solve problems related to area, volume, and physical quantities.
Having a clear grasp of these topics will enable you to tackle a wide variety of problems, from simple calculations to more complex applications, effectively demonstrating your ability to apply the core principles of the subject.
Important Formulas for the Midterm
One of the keys to succeeding in the upcoming assessment is familiarity with the essential mathematical formulas that are frequently applied throughout the test. These formulas form the foundation for solving various types of problems, and knowing them well can save valuable time during the challenge. Below are the critical formulas you should have at your fingertips to approach the questions confidently.
Derivatives and Rates of Change
The derivative is a central concept in the subject, and several key formulas will help you calculate rates of change and slopes. Some important ones include:
- Power Rule: ( frac{d}{dx} x^n = nx^{n-1} )
- Product Rule: ( frac{d}{dx} (u cdot v) = u’ cdot v + u cdot v’ )
- Quotient Rule: ( frac{d}{dx} left( frac{u}{v} right) = frac{u’ cdot v – u cdot v’}{v^2} )
- Chain Rule: ( frac{d}{dx} f(g(x)) = f'(g(x)) cdot g'(x) )
Integrals and Areas
Integration is another core area, particularly when it comes to calculating areas and accumulated quantities. Here are some essential formulas:
- Indefinite Integral of Power Functions: ( int x^n , dx = frac{x^{n+1}}{n+1} + C ) (for (n neq -1))
- Definite Integral: ( int_a^b f(x) , dx = F(b) – F(a) ), where ( F ) is the antiderivative of ( f )
- Area Under a Curve: Use the definite integral to find the area between the curve and the x-axis.
Mastering these formulas will allow you to approach a wide variety of problems efficiently, ensuring that you can solve them correctly and in a timely manner.
Common Mistakes to Avoid
Even when you’re well-prepared, it’s easy to make small mistakes that can significantly affect your performance. Being aware of these common errors can help you avoid them and approach problems more carefully. Below are some of the most frequent pitfalls and how to steer clear of them during the assessment.
- Rushing Through the Questions – It’s tempting to move quickly, but this often leads to careless mistakes. Take your time to read each question thoroughly and ensure you understand what is being asked before attempting a solution.
- Misapplying Formulas – Applying the wrong formula or using it incorrectly is a common error. Always double-check that you are using the appropriate method for each problem, and remember to follow each step logically.
- Skipping Steps in Solutions – Some students try to shortcut their work to save time, but skipping steps can lead to incorrect answers. Write out each step clearly, even if it seems obvious, to avoid mistakes.
- Not Checking Units – In problems involving measurements, it’s easy to overlook units of measurement. Ensure that you convert or maintain consistent units throughout the problem to avoid errors.
- Overlooking Negative Signs – A small oversight, like forgetting a negative sign, can change the entire result of a calculation. Always double-check your arithmetic and signs, especially when dealing with subtraction or division.
- Ignoring Graphs and Diagrams – Sometimes, questions will include graphs or diagrams that provide crucial information. Be sure to carefully interpret and use these visuals to inform your answers.
By keeping these mistakes in mind, you can approach the test with a more careful and methodical mindset, improving both your accuracy and efficiency.
Time Management Tips for the Exam
Proper time management is essential when facing a challenging assessment. Without an efficient strategy, you might find yourself rushing through questions or spending too much time on one particular problem. Knowing how to allocate your time effectively will help you maintain a steady pace and ensure that you can complete all sections within the time limits.
Plan Your Time Wisely
Before diving into the questions, take a few moments to review the entire test. This will give you an idea of the types of problems you’ll encounter and how much time you should allocate for each section. Prioritize questions based on difficulty and length, and decide which parts require more careful thought.
- Start with the questions that seem easier to boost your confidence.
- Leave more time for complex problems that may require detailed solutions.
- Avoid spending too long on any one question–move on if you’re stuck and return to it later if time permits.
Practice Under Time Constraints
Simulating test conditions during your preparation can help you get used to the time pressure. Take practice tests and try to complete them within the allotted time frame. This will help you develop a sense of pacing and identify areas where you may need to improve your speed or efficiency.
Remember, staying calm and focused is just as important as knowing the material. By managing your time well, you’ll be able to maximize your performance and reduce unnecessary stress.
How to Approach Multiple Choice Questions
Multiple choice questions can often seem straightforward, but they require careful attention to detail. Each option may contain subtle clues or distractions that can lead to errors if not approached methodically. Knowing how to handle these questions effectively will help you maximize your score while avoiding common pitfalls.
Read Each Question Carefully
Before considering the answer choices, take your time to thoroughly read the question. Pay attention to every word, especially keywords like “not,” “except,” or “always,” which can completely change the meaning of the question. Understanding exactly what is being asked is the first step in eliminating incorrect answers.
- Underline or highlight key terms to focus your attention.
- Look for any wording that suggests multiple options may seem correct but only one is fully accurate.
Eliminate Clearly Wrong Answers
Once you’ve read the question, begin by eliminating any choices that are clearly incorrect. Even if you’re unsure about the right answer, removing obviously wrong options increases your chances of guessing correctly. This strategy narrows down your choices and helps you focus on the more plausible options.
- Look for extreme words like “always” or “never,” which are often incorrect.
- Compare the remaining options for subtle differences and identify the most accurate response.
By following a structured approach, you can tackle multiple choice questions with more confidence, ensuring that you make the best possible choice every time.
Strategies for Answering Free Response Questions
Free response questions test your ability to solve problems in a detailed and structured manner. Unlike multiple choice questions, these require not only the correct solution but also a clear explanation of your thought process. A methodical approach to these questions can help ensure that you provide all necessary steps and explanations to demonstrate your understanding.
One of the most important strategies is to break down each question into manageable parts. Organize your thoughts before jumping into calculations, and make sure you fully understand what is being asked. A clear and logical solution can often be the key to earning full credit.
Step-by-Step Process
When tackling free response questions, it is crucial to follow a systematic approach to avoid missing any key steps in the solution. Below is an example of how to approach each problem:
| Step | Action |
|---|---|
| 1 | Read the Question Carefully – Understand exactly what is being asked and identify any key information provided. |
| 2 | Organize Your Thoughts – Break the problem into smaller, manageable parts. Think about which formulas or methods to apply. |
| 3 | Show All Work – Write out every step of your solution, even if it seems simple. This demonstrates your logical reasoning. |
| 4 | Check Your Answer – Review the problem and your solution. Ensure that your answer is reasonable and answers the question completely. |
By using this structured approach, you can ensure that your response is both complete and clear, helping you to earn all possible points for each question. Always remember that clarity and thoroughness are key when answering free response questions.
Reviewing Past AP Calculus Exams
Reviewing previous assessments is one of the most effective ways to prepare for an upcoming test. By analyzing past questions, you can gain insight into the types of problems commonly asked and the format in which they appear. This allows you to identify recurring themes and familiarize yourself with the overall structure, which helps in building confidence and refining problem-solving strategies.
Identify Common Question Types
Going through past papers enables you to recognize which topics are frequently covered. While the specific questions may vary, the concepts remain largely the same. Pay special attention to areas where you might have struggled in the past and focus on mastering these topics.
- Look for problems that test specific mathematical techniques or concepts.
- Practice the same type of problems multiple times to reinforce your understanding and speed.
Understand the Grading Approach
In addition to practicing questions, reviewing the scoring guidelines of past assessments is equally important. This allows you to understand what examiners are looking for in each response and how points are awarded for each step in the solution. Knowing how to present your work effectively can help you maximize your score, even if the final answer isn’t entirely correct.
- Focus on how the explanation and reasoning behind the solution contribute to the score.
- Learn to write clear, concise responses that demonstrate your thought process.
By reviewing past assessments, you can ensure that you are fully prepared for the challenges ahead, equipped with both knowledge and strategic insight into how to approach each question.
Using Online Resources for Practice
The internet offers a wealth of tools and platforms that can enhance your preparation. Online resources provide access to a wide variety of practice problems, tutorials, and explanations that can help you build both your skills and confidence. By incorporating these resources into your study routine, you can improve your understanding and performance in a structured way.
Explore Interactive Problem Solvers
Interactive websites allow you to practice solving problems while receiving immediate feedback. These platforms often offer step-by-step solutions, which help you understand the reasoning behind each answer. Additionally, they provide a wide range of difficulty levels, ensuring that you can gradually challenge yourself as you progress.
- Problem sets that target specific skills can reinforce your knowledge of key concepts.
- Instant feedback helps identify mistakes early, giving you the chance to correct them before they become habits.
Watch Educational Videos
Many websites offer video tutorials that break down complex topics into manageable sections. These videos often include visual explanations and detailed walkthroughs of common problems, making it easier to grasp difficult concepts. They can be especially useful for visual learners who prefer to see the process in action.
- Visual aids such as graphs and animations can simplify abstract ideas.
- Clear explanations allow you to follow along at your own pace and review tricky topics multiple times.
By making the most of online platforms, you can supplement your textbook studies and gain valuable practice outside of traditional study materials.
How to Improve Your Mathematical Skills
Enhancing your mathematical abilities requires consistent practice, strategic learning, and a deep understanding of fundamental concepts. By focusing on core techniques and actively seeking to solve a variety of problems, you can improve both your problem-solving efficiency and your overall comprehension of complex topics. The key is to approach learning systematically and stay committed to steady improvement.
Build a Strong Foundation
Before attempting more advanced problems, ensure that you have a solid grasp of the basic concepts. Mastery of foundational topics allows you to tackle more complex questions with confidence. Reinforce your understanding by reviewing key concepts regularly and solving simple problems to keep them fresh in your mind.
- Review core techniques such as differentiation and integration, as these are fundamental to more advanced topics.
- Understand the underlying principles behind each method, rather than simply memorizing formulas.
- Work on building mental math skills to solve problems more efficiently.
Practice Regularly
Regular practice is essential to improving your abilities. The more problems you solve, the more you will recognize patterns and strategies that can be applied across different scenarios. Challenge yourself by gradually increasing the difficulty level of the problems you tackle. This helps develop both speed and accuracy.
- Set aside dedicated time for daily practice to keep concepts fresh and reinforce skills.
- Focus on solving problems from a variety of sources to expose yourself to different styles of questions.
- Don’t just solve the problems–take time to review your mistakes and understand where you went wrong.
By combining regular practice with a deep understanding of fundamental concepts, you can steadily improve your mathematical abilities and become more confident in solving complex problems.
Sample Problems and Step-by-Step Solutions
Working through sample problems and analyzing detailed solutions is a highly effective way to strengthen your understanding of complex topics. By breaking down problems into smaller, manageable steps, you can develop the skills necessary to approach similar questions with confidence. This method not only helps you see how to solve a problem but also deepens your understanding of the underlying concepts involved.
Below are examples of problems followed by step-by-step explanations. These will guide you through the problem-solving process, highlighting key techniques and strategies along the way. It’s essential to follow each step closely to see how the solution unfolds logically and efficiently.
Problem 1: Finding the Rate of Change
Problem: Given the function f(x) = 3x² + 2x – 5, find the rate of change at x = 4.
Step 1: Differentiate the function. The derivative of f(x) = 3x² + 2x – 5 is f'(x) = 6x + 2.
Step 2: Substitute x = 4 into the derivative to find the rate of change:
f'(4) = 6(4) + 2 = 24 + 2 = 26
Solution: The rate of change at x = 4 is 26.
Problem 2: Solving a Definite Integral
Problem: Compute the integral of f(x) = 2x + 1 from x = 0 to x = 3.
Step 1: Set up the integral: ∫(2x + 1) dx from 0 to 3.
Step 2: Find the antiderivative of the function: ∫(2x + 1) dx = x² + x.
Step 3: Evaluate the antiderivative at the bounds of the integral:
[x² + x] from 0 to 3 = (3² + 3) – (0² + 0) = 9 + 3 = 12
Solution: The value of the definite integral is 12.
By practicing these types of problems and reviewing each step in detail, you’ll be able to master key techniques and apply them more effectively in future challenges.
Understanding the Scoring System
When preparing for assessments, it is crucial to understand how the scoring system works. The way your performance is evaluated directly impacts your results, and knowing the criteria can help you strategize and manage your time more effectively. Scoring is not only based on correctness but also on how thoroughly you demonstrate your understanding of key concepts. In most cases, points are awarded for each correctly solved problem, with partial credit given for showing work or demonstrating a logical approach, even if the final answer is incorrect.
Typically, the structure of the grading system involves two main components: objective questions and open-ended problems. Each part of the assessment contributes a specific percentage to the overall score. Below, we will discuss the scoring details for both types of questions and explain how each section influences your final result.
Objective Questions Scoring
Objective questions are those that require you to select the correct answer from a list of options. These are generally scored based on whether or not the answer is correct, with no partial credit for incorrect answers. Each question is assigned an equal weight, and you are awarded full points for a correct response.
Open-Ended Problems Scoring

Open-ended problems require you to show your work and reasoning. Even if you don’t arrive at the correct final answer, points are often awarded for demonstrating a solid understanding of the process. The scoring for these types of questions typically involves the following elements:
- Correct setup and approach: Points are awarded for correctly identifying the method or formula needed to solve the problem.
- Accurate calculations: If you make a mistake in your calculations, partial credit may still be given for using the correct approach.
- Final answer: Full credit is typically given if the final result is correct, but partial points are given for intermediate steps.
By understanding the breakdown of how points are awarded, you can focus on both the accuracy of your answers and the clarity of your reasoning. Proper preparation with this in mind will help you maximize your score.
How to Stay Calm During the Exam
Staying composed and focused during a challenging assessment is essential for performing at your best. Stress and anxiety can hinder your ability to think clearly and solve problems efficiently. Learning how to manage your emotions and maintain a calm mindset will not only help you avoid common mistakes but also boost your confidence. By practicing strategies for relaxation and mental focus, you can ensure that you’re in the best possible state to tackle any question that comes your way.
There are various techniques that can help you stay relaxed under pressure. These methods can range from physical techniques, such as controlled breathing, to mental approaches like positive visualization. Developing a routine for calming yourself before and during the test will allow you to remain level-headed throughout the entire process.
Breathing Techniques
When you start to feel overwhelmed, it’s important to focus on your breath. Deep breathing exercises can help lower stress levels and provide mental clarity. Try inhaling deeply through your nose for a count of four, holding for four seconds, and exhaling slowly for a count of four. Repeat this process a few times to regain focus and calm your nerves.
Visualization and Positive Thinking
Visualization can be a powerful tool for mental preparation. Before the assessment begins, take a moment to visualize yourself answering questions confidently and successfully. This positive imagery can enhance your mindset and reduce anxiety. Additionally, remind yourself of the hard work you’ve put in and your ability to handle the challenges ahead.
By using these techniques, you can improve your ability to manage pressure and maintain a clear, calm focus throughout your assessment.
What to Bring on Exam Day
Preparing for a test involves more than just studying the material; knowing what to bring on the day of the assessment is equally important. Ensuring that you have all the necessary items can help reduce stress and prevent any last-minute surprises. From writing tools to identification, each item plays a crucial role in ensuring that you’re fully equipped to succeed.
Here’s a list of essential items to bring with you, so you can focus on the content without worrying about missing any critical tools:
Essential Items to Pack
| Item | Purpose |
|---|---|
| Pencil(s) | For answering questions, especially multiple choice or free response. |
| Eraser | To correct any mistakes while working through problems. |
| Calculator | If allowed, for calculations and graphing. |
| Identification | To verify your identity and meet the testing requirements. |
| Watch or Timer | To manage your time effectively during the assessment. |
| Extra Batteries | If using a battery-operated device, make sure you have spares. |
Additional Items to Consider
Depending on the specific rules of the assessment, there may be other items you should consider bringing:
- Snack or Water: To stay refreshed and focused during the test.
- Comfortable Clothing: Dressing in layers to ensure comfort during the assessment.
- Positive Attitude: Mental preparedness can be as important as physical readiness.
By making sure you have everything you need, you can walk into the testing environment feeling confident and prepared, allowing you to focus solely on the tasks at hand.
How to Analyze Your Results After the Exam
Once you’ve completed a test, it’s crucial to take the time to carefully evaluate your performance. Analyzing your results helps you identify strengths and areas that need improvement. This process can be invaluable for refining your skills and preparing for future challenges. Understanding where you did well and where you faced difficulties allows you to adjust your study strategy and approach to similar problems going forward.
Here are the key steps to effectively analyze your performance:
Steps for Post-Test Evaluation

- Review Mistakes: Start by focusing on questions you answered incorrectly. Look at the explanations or solutions to understand where you went wrong.
- Identify Patterns: Check if there are recurring topics or concepts that you struggled with. This can help you pinpoint areas that need further study.
- Evaluate Time Management: Assess how well you managed your time. Did you rush through certain sections? Did you spend too much time on others?
- Consider Your Confidence Level: Reflect on how sure you felt about your answers. If you guessed or weren’t sure about a response, take note for future practice.
How to Use Your Results for Improvement
- Focus on Weak Areas: Make a list of topics or question types that caused difficulty, and review them in more detail.
- Practice Similar Problems: Work on additional exercises that are similar to the ones you missed, ensuring you understand the underlying concepts.
- Seek Feedback: If available, ask your instructor or peers for feedback on your mistakes, as they may provide valuable insights.
- Track Your Progress: Keep a record of your performance on each assessment. Monitoring improvement over time can be motivating and give you a clear sense of your growth.
By carefully evaluating your results, you turn every assessment into a learning experience, helping you build a stronger foundation for future success.
Preparing for the Next AP Calculus Exam
Successfully preparing for any test requires consistent effort, thoughtful review, and strategic planning. The key to improving your performance on future assessments lies in building upon past experiences. After completing an assessment, it’s essential to use that experience to inform your preparation for the next challenge. A proactive approach, incorporating regular practice, concept reinforcement, and time management techniques, can lead to significant improvements.
Developing a Comprehensive Study Plan
Start by creating a detailed study schedule that covers all topics you need to review. This will help you organize your time effectively and ensure that no area is overlooked. Incorporate a mix of theory review, practice questions, and timed drills to simulate real test conditions.
- Set Clear Goals: Identify specific areas where you need improvement and prioritize them in your study plan.
- Use Different Study Methods: Combine reading notes, watching instructional videos, and practicing problems to strengthen your understanding.
- Practice Under Time Constraints: Simulate testing conditions by timing yourself when solving problems to build your pacing skills.
Focus on Conceptual Understanding
Understanding the underlying principles is far more important than memorizing formulas. A solid grasp of core concepts allows you to tackle even unfamiliar questions more effectively. To reinforce your understanding:
- Review Key Theories: Ensure you fully understand the fundamental concepts and how they connect to more complex problems.
- Work Through Challenging Problems: Don’t shy away from difficult questions. Tackle them head-on and review your solutions carefully.
- Clarify Doubts: If there are concepts you find confusing, seek help from teachers, tutors, or peers to clarify your understanding.
By staying disciplined and focused, and by consistently evaluating and adjusting your approach, you’ll be well-prepared for the next assessment and more confident in your abilities.