Preparing for an important assessment in mathematics can be a challenging yet rewarding experience. Whether you’re tackling theoretical problems or applying formulas to solve complex situations, understanding the foundational principles is crucial for success. This section will help you review essential topics, boost your confidence, and sharpen your problem-solving abilities.
Focusing on the most critical aspects of your course will allow you to address common challenges and recognize patterns in questions. From learning core principles to refining practical skills, each step will contribute to a stronger grasp of the subject matter. By reviewing key strategies and techniques, you can approach each task with greater clarity and efficiency.
Emphasizing practice will further enhance your ability to apply concepts in different scenarios. Mastering key topics and avoiding frequent pitfalls will ensure you’re well-prepared when it’s time to demonstrate your knowledge.
Geometry Midterm Exam Study Guide Answers
When preparing for an important assessment in the field of mathematics, having a clear understanding of fundamental principles is essential. This section will help you tackle various types of problems by offering insight into essential topics, providing examples, and highlighting strategies to approach different question formats.
Each problem type requires a unique method for solving, and practicing these methods will increase your ability to respond effectively under timed conditions. By reviewing common question structures and applying proven techniques, you will build the confidence necessary to approach the test with a structured mindset.
Additionally, reinforcing your understanding of key concepts will improve your speed and accuracy, making it easier to identify critical steps in solving each problem. The more familiar you become with the material, the better equipped you’ll be to manage complex situations and ensure successful outcomes.
Understanding Key Geometry Concepts
A strong grasp of essential principles is crucial when working with shapes, measurements, and spatial relationships. To solve complex problems, it’s important to have a solid foundation in the fundamental ideas that drive this area of mathematics. From the basic properties of different figures to the relationships between angles and lines, mastering these concepts will provide you with the tools needed to succeed in more advanced tasks.
Key ideas such as area, perimeter, volume, and angles serve as the building blocks for more complex reasoning and problem-solving. Understanding these core principles allows you to break down more intricate questions into manageable steps, making it easier to apply formulas and derive solutions. As you review these fundamental concepts, aim to connect theory with real-world applications to deepen your comprehension and strengthen your problem-solving skills.
How to Solve Geometry Problems
Approaching a mathematical challenge requires a structured and logical method to ensure accuracy and efficiency. Whether you’re dealing with simple shapes or complex figures, each problem can be broken down into smaller, manageable parts. By following a step-by-step process, you’ll be able to identify the right approach and apply the necessary techniques to find the solution.
Break Down the Problem

The first step in solving any mathematical problem is to carefully read and analyze the question. Identify what is given and what needs to be found. Look for important clues such as numerical values, relationships between different elements, and key properties of shapes. This will give you a clear roadmap for how to proceed.
Apply Relevant Formulas and Theorems
Once the problem is understood, use the appropriate formulas and principles to calculate the unknown values. This could involve working with areas, volumes, or angles. It’s essential to remember the key relationships between different elements of figures, such as the Pythagorean theorem or properties of parallel lines. Using these well-established formulas will guide you toward the correct solution.
Important Formulas for Your Exam

Having a solid understanding of the essential equations and relationships is key to successfully solving problems in mathematics. The ability to recall and apply the correct formulas can make a significant difference when working with various shapes, measurements, and spatial relationships. Familiarizing yourself with the most commonly used expressions will save time and help ensure accuracy when tackling questions.
Area and Perimeter of Shapes are fundamental concepts that you will encounter often. For example, the area of a rectangle is calculated by multiplying its length and width, while the perimeter is the sum of all its sides. These basic formulas lay the groundwork for more complex tasks, allowing you to work through a wide range of questions efficiently.
Volume and Surface Area formulas are also vital for solving problems involving three-dimensional objects. Understanding how to calculate the volume of solids like cubes, spheres, and cylinders is crucial, as is knowing how to determine their surface areas for various practical applications.
Mastering these core formulas will not only help you solve problems more effectively but also improve your confidence and speed during problem-solving.
Mastering Geometry Proof Techniques
In mathematical problem-solving, constructing logical arguments is an essential skill. The ability to prove a statement or solve a problem through reasoning not only demonstrates understanding but also provides a deeper insight into the relationships between various elements. Developing a systematic approach to proofs will help you address challenges more effectively and with greater clarity.
Start with Known Information
To build a solid proof, begin by identifying all the given facts and assumptions. Break down the problem into smaller parts and focus on what is already known. This can include values, relationships, or properties of geometric shapes. From here, you can begin to draw logical conclusions based on the rules and principles that apply to these elements.
Use Logical Reasoning and Theorems
The next step involves applying established rules, theorems, and properties to support your reasoning. For instance, if you’re working with angles, recall the properties of complementary or supplementary angles. Similarly, using congruence or similarity can help you relate different parts of a figure and draw conclusions based on known facts. Each step should follow naturally from the previous one, ensuring that your argument is valid and well-supported.
Common Mistakes to Avoid

When solving mathematical problems, it’s easy to make small but significant errors that can lead to incorrect results. Recognizing and understanding these common pitfalls is an important part of improving accuracy. Being aware of these mistakes can help you avoid them and approach each problem more effectively.
1. Misreading the Problem
One of the most frequent mistakes is misunderstanding the question or overlooking key information. It’s essential to read the problem carefully and identify what is being asked before jumping into the solution.
- Ensure you know what values are given and what you need to find.
- Pay attention to details such as units of measurement or specific conditions in the problem.
- Check for hidden clues or relationships between elements in the problem statement.
2. Incorrectly Applying Formulas

Another common mistake is using the wrong formula or applying it incorrectly. Always double-check the formula you plan to use and ensure it’s appropriate for the given situation.
- Make sure you understand the meaning of each variable in the formula.
- Don’t mix up formulas for different shapes or dimensions.
- Ensure you are applying formulas to the correct parts of a figure.
3. Skipping Steps in the Calculation
Rushing through calculations or skipping intermediate steps can lead to errors in the final solution. Taking time to show your work and verify each calculation will help prevent mistakes.
- Write out all steps clearly, especially when working with multiple operations.
- Check your arithmetic and algebra at each stage of the problem.
- Ensure you haven’t skipped any logical steps in deriving the solution.
Tips for Efficient Time Management
Effective time management is essential when facing a challenging assessment. By using your time wisely, you can ensure that you cover all necessary material and avoid unnecessary stress. With the right approach, you can work through problems systematically and complete tasks within the allotted time frame.
1. Prioritize Tasks
One of the first steps to managing your time effectively is determining which tasks need to be addressed first. Focus on the most important or time-consuming problems first, and leave simpler tasks for later.
- Start with the questions that carry the most weight or require more complex solutions.
- If a question feels particularly difficult, break it down into smaller parts and tackle them step by step.
- Leave easier or quicker tasks for the end to ensure you have time for more challenging problems.
2. Practice Under Time Constraints
Simulating timed conditions during your preparation can help you build the stamina and speed required for the actual test. By practicing in a time-limited environment, you’ll become more accustomed to working under pressure and learn how to pace yourself effectively.
- Set a timer and try to complete practice problems within the expected time limits.
- Review your performance and identify areas where you spent too much time.
- Adjust your approach and find strategies to answer questions more quickly without sacrificing accuracy.
3. Stay Calm and Focused
Maintaining focus and staying calm are key components of good time management. Avoid getting bogged down by one difficult question; instead, move on and come back to it later if needed.
- If you encounter a challenging problem, take a deep breath and stay composed.
- Don’t dwell on mistakes or spend too much time on any single task.
- Stay mindful of the clock and monitor how much time you have left to ensure you’re staying on track.
How to Approach Word Problems
Word problems can often seem overwhelming, but with a clear strategy, they become much more manageable. The key to solving these types of questions is breaking them down into smaller, more understandable steps. By identifying the important information and applying the correct methods, you can solve even the most complex word problems with ease.
1. Read the Problem Carefully

The first step in solving any word problem is to read it thoroughly. Make sure you understand the scenario being presented and identify the key details.
- Underline or highlight important numbers, conditions, and relationships mentioned in the problem.
- Pay attention to any specific questions or instructions that are part of the problem.
- Don’t rush through the text–take the time to fully grasp the situation before jumping to conclusions.
2. Identify What You Need to Find
Once you have a clear understanding of the problem, determine what is being asked. This will guide your approach and help you focus on the relevant parts of the problem.
- Look for keywords that indicate what you’re solving for, such as “find,” “calculate,” or “determine.”
- Identify the unknowns and what you already know about them.
- Write down what needs to be solved for and make sure you have all the necessary information to do so.
3. Translate Words into Mathematical Expressions
Next, translate the given information into a form that can be worked with mathematically. This could involve setting up equations, diagrams, or charts.
- Convert the relationships described in the problem into mathematical symbols, such as variables or formulas.
- If needed, draw a diagram to represent the situation visually–this can help clarify complex relationships.
- Remember that organizing the information properly is essential for simplifying the problem-solving process.
4. Solve and Check Your Work
Finally, solve the problem step by step, and don’t forget to check your solution to ensure accuracy.
- Work through the mathematical operations carefully, following the correct order of operations.
- After solving, review your answer in the context of the problem–does it make sense?
- If time allows, double-check your calculations and ensure that no details were overlooked.
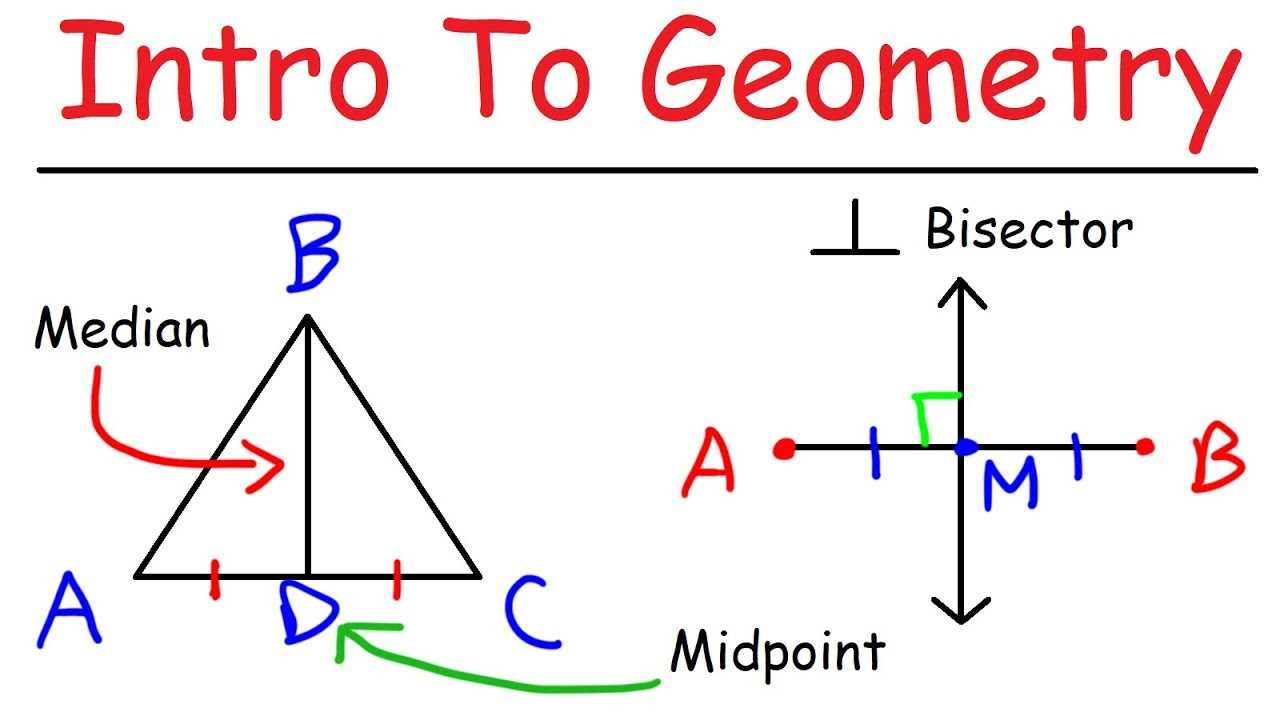
Diagrams and Their Importance
Visual representations play a crucial role in understanding complex problems. They provide a clear picture of the relationships between different elements, making it easier to apply logical reasoning. By translating abstract concepts into tangible visuals, diagrams simplify the problem-solving process and help identify patterns or key features that might otherwise be overlooked.
When faced with a challenge, always consider how a diagram can enhance your understanding of the situation. Whether it’s illustrating shapes, lines, or angles, a well-drawn diagram can make it much easier to visualize and solve the problem. It’s not just about drawing–it’s about using that visual tool to better structure your thinking and approach.
In many cases, diagrams can provide insights that verbal descriptions or formulas alone cannot. By actively engaging with the diagram, you can spot relationships, detect symmetries, and test assumptions in a more interactive way. This approach can save time and reduce the likelihood of making errors during calculations or logical deductions.
Moreover, diagrams offer a way to organize information efficiently. They serve as a reference point, helping to keep track of multiple variables and showing how they are interrelated. When faced with multiple steps or complex conditions, having a clear visual representation can serve as an anchor, guiding you through each stage of the solution process.
Strategies for Memorizing Theorems
Remembering key principles and rules is vital when preparing for any assessment. Theorems often form the foundation of problem-solving, so mastering them ensures you can approach challenges confidently and accurately. However, memorizing complex concepts can be daunting. Fortunately, with the right techniques, it becomes easier to commit these principles to memory and recall them effectively when needed.
1. Break Down Complex Theorems

Large or intricate theorems can be overwhelming, but breaking them into smaller, more digestible pieces can make them easier to memorize. Focus on understanding the individual parts first before trying to memorize the entire statement.
- Divide the theorem into clear segments: premise, statement, and conclusion.
- Understand the meaning of each part and how they connect with each other.
- Once you grasp the logic behind the theorem, it becomes easier to remember the full statement.
2. Use Mnemonics and Visualization
Mnemonics and visual aids are powerful tools for memory retention. Creating associations between theorems and memorable phrases or images can help you recall them more easily during problem-solving.
- Develop acronyms or short phrases that summarize the essence of a theorem.
- Visualize the theorem’s application in practical scenarios to solidify the concept in your mind.
- Draw diagrams or charts that relate to the theorem’s conditions and conclusions.
3. Repetition and Active Recall
Constant repetition is one of the most effective ways to memorize theorems. Active recall, where you test your memory without looking at the content, is particularly useful in reinforcing what you’ve learned.
- Write the theorems out regularly, without referencing notes, to test how much you’ve retained.
- Use flashcards or apps that promote spaced repetition to strengthen memory retention.
- Recite theorems aloud and try to explain them in your own words to ensure deep understanding.
4. Organize Theorems with a Table
Creating a structured reference sheet or table can help you organize theorems in a way that makes them easier to understand and memorize. Group similar concepts together, and highlight key conditions and results to provide a clear overview.
| Theorem | Conditions | Conclusion |
|---|---|---|
| Example Theorem 1 | Condition 1, Condition 2 | Result of the theorem |
| Example Theorem 2 | Condition A, Condition B | Result of the theorem |
Practice Problems to Solve
Practicing a variety of problems is one of the best ways to improve your problem-solving skills. Regularly tackling challenges allows you to apply theoretical knowledge in real-world scenarios, reinforcing your understanding and boosting confidence. By working through different types of exercises, you can identify areas of weakness and focus your efforts on improving them. Below are several problems designed to strengthen your skills in key areas, ranging from basic principles to more complex scenarios.
Example Problems
Each problem helps to reinforce core concepts and encourages active learning through hands-on practice. Take your time to solve each one, and use diagrams where necessary to visualize the situation.
| Problem | Details | Solution Steps |
|---|---|---|
| Problem 1 | Find the area of a triangle with a base of 10 cm and a height of 5 cm. |
|
| Problem 2 | Calculate the circumference of a circle with a radius of 7 cm. |
|
| Problem 3 | Determine the sum of the interior angles of a quadrilateral. |
|
Breakdown of Common Questions
In any problem-solving process, recognizing recurring patterns and frequently asked questions is a key step to mastering the subject. This section will break down some of the most common types of questions encountered in mathematical assessments. By understanding these problem types and their solutions, you can approach similar challenges with confidence. Focus on the concepts behind each question to better apply your knowledge in different situations.
Understanding Key Shapes and Their Properties

One of the most frequent topics involves identifying properties of basic shapes, such as squares, triangles, circles, and polygons. Problems often ask for area, perimeter, or angle measurements. Knowing the fundamental formulas for each shape and understanding their characteristics is essential for solving these questions efficiently.
Working with Angles and Ratios
Another common type of question focuses on angles, including supplementary, complementary, and vertical angles, as well as angle relationships within geometric figures. Problems may ask you to find unknown angles based on known values or apply angle relationships in real-world contexts. Recognizing the patterns in angle-related problems allows you to solve them systematically.
How to Read and Interpret Questions

Understanding the language and structure of problems is crucial to solving them accurately. Many times, the difficulty of a question lies not in the complexity of the math involved but in the way it is phrased. Being able to break down a question, identify key information, and focus on what is being asked will lead to clearer and faster solutions. This section offers practical strategies for analyzing and interpreting different types of problems effectively.
Identifying Key Information
The first step in interpreting any problem is identifying the most important details. Often, questions will provide extra information that isn’t necessary for solving the problem. The challenge lies in filtering out the unnecessary data and focusing on the key components that directly contribute to the solution.
Breaking Down Complex Questions
Complex problems can be intimidating at first glance. However, breaking them down into smaller, manageable parts can make them much easier to tackle. Look for patterns, relationships, or formulas that apply to different sections of the question. Step by step, dissect the problem to identify what is being asked in each part.
| Common Question Type | Key Elements to Focus On | Interpretation Tips |
|---|---|---|
| Word Problems | Numbers, units, relationships between quantities | Convert words into equations or diagrams for clarity |
| Formula Application | Known values, unknown variables, applicable formulas | Identify which formula to apply and substitute values accurately |
| Geometry Figures | Dimensions, angles, geometric relationships | Draw and label figures to visualize relationships |
Using Graphing Tools in Geometry
Graphing tools are invaluable resources when solving spatial problems, as they allow you to visualize abstract concepts and relationships between various elements. Whether you’re working with shapes, lines, or angles, these tools help clarify complex ideas, making them easier to understand and solve. By plotting points, lines, and curves, graphing aids in identifying geometric properties, distances, and intersections, providing a clearer approach to tackling questions.
Benefits of Using Graphing Tools
Graphing tools allow you to see a problem from multiple perspectives. They make it easier to interpret data, check your work, and visualize how different components interact within a given figure. By turning a theoretical problem into a visual representation, you can identify patterns and relationships more effectively, leading to faster and more accurate solutions.
Common Graphing Tools and Their Applications
There are several types of graphing tools, both digital and manual, that can assist in solving problems. Graphing calculators, computer software, and even graph paper can help you plot points, lines, and curves. Each of these tools has specific functions, such as calculating slopes, finding intersections, or measuring distances, which are essential when solving spatial questions.
What to Do the Night Before the Exam
As the day before an important assessment approaches, the focus should shift towards preparing yourself mentally and physically for the challenge ahead. It’s crucial to approach the evening with a calm, organized mindset, allowing you to reflect on what you’ve learned without overloading yourself. This is the time to reinforce key concepts and ensure you’re in the right headspace for the task at hand.
Review Key Concepts and Formulas
Take some time to quickly review the most important concepts, theorems, and formulas that you might encounter. This isn’t the moment for deep studying or trying to learn new material, but rather for reinforcing what you already know. Focus on understanding how these ideas connect and their practical applications, as this will help you approach the questions more confidently the next day.
Get a Good Night’s Rest
Perhaps the most important aspect of preparation the night before is ensuring you get enough sleep. Rest is essential for memory consolidation and mental clarity. A well-rested mind performs better under pressure, so avoid staying up late cramming and instead aim for a full, restful night of sleep. This will allow you to be sharp, focused, and ready for the challenges that await.
Final Review Checklist for Geometry Exam
As the assessment approaches, it’s important to have a structured approach to ensure that all the essential topics and skills have been adequately reviewed. A final review checklist is a helpful tool to ensure you are fully prepared and focused. This checklist should be used to confirm that you’ve covered all necessary material, brushed up on key strategies, and are ready for the challenges ahead.
Key Areas to Review
- Understand Key Theorems: Review important principles and how they apply to various problems. Make sure you can recall them and know when to use them.
- Practice Problem Solving: Work through a variety of problems, including those that challenge you. Focus on both computational and conceptual questions.
- Formula Memorization: Ensure that all necessary formulas are at your fingertips and that you know how to apply them in different scenarios.
- Visualize with Diagrams: Familiarize yourself with interpreting diagrams quickly. Practice sketching them yourself if needed.
Test-Taking Strategies
- Time Management: Practice timing yourself on questions. Plan how much time you’ll spend on each section and stick to it during the assessment.
- Review Previous Mistakes: Go over past errors to ensure you don’t make the same mistakes again. Understand why you got certain problems wrong.
- Stay Calm and Confident: Trust your preparation. A calm mindset can help you think more clearly during the test.