When preparing for a critical evaluation in mathematics, it’s important to focus on mastering fundamental concepts and key problem-solving techniques. The path to success often involves a deep understanding of various theories, formulas, and strategies. By breaking down complex problems into simpler steps, you can build confidence and improve accuracy under pressure.
Every topic covered in this assessment presents unique challenges that require both knowledge and strategy. From algebraic principles to spatial reasoning, each section demands a different approach. Understanding the relationships between shapes, angles, and calculations will be crucial in addressing the most challenging sections effectively.
Effective preparation means identifying areas of strength while also focusing on aspects that need more attention. Reviewing practice problems, focusing on common pitfalls, and refining your approach will significantly boost your readiness. Whether it’s solving equations or applying theorems, every moment spent practicing is a step towards achieving mastery.
By dedicating time to review, practicing under timed conditions, and seeking clarification on difficult concepts, you’ll improve both speed and accuracy, making you well-prepared for the challenges ahead.
Geometry Final Exam Study Guide Answers
Preparing for an important mathematics assessment requires a clear understanding of the essential concepts and the ability to apply them effectively in problem-solving. Each section of the evaluation demands a different set of skills, from logical reasoning to spatial visualization. Focusing on mastering key topics ensures confidence when addressing a variety of questions.
Key Concepts to Focus On
It’s crucial to understand the core principles behind each mathematical concept. Whether working with shapes, angles, or calculations, a strong grasp of the fundamentals will allow for easier manipulation of complex problems. Topics such as properties of triangles, relationships between lines and angles, and area and volume formulas often make up a large portion of the test. In addition, practice with these concepts will sharpen your ability to quickly identify the most efficient method of solving any given question.
Strategies for Effective Problem Solving
To excel, it’s important to have a strategic approach when working through problems. Start by analyzing the question carefully to determine the most suitable method. Use diagrams when necessary to visualize spatial relationships, and remember that breaking down a problem into smaller parts can make the process more manageable. Regular practice under timed conditions will also help develop the speed and precision needed to succeed in the assessment.
Key Topics for Geometry Finals
Success in a mathematics assessment relies on mastering the fundamental principles that form the foundation of the subject. Focusing on key topics ensures that you’re equipped to handle a variety of questions with confidence. These topics often require both conceptual understanding and practical application, making it essential to approach each one with a clear strategy.
Several core areas are commonly tested, each with its own set of challenges. Key areas such as angles, shapes, and their properties are central to many problems. Additionally, spatial reasoning, transformations, and the ability to calculate areas and volumes will likely feature prominently. By focusing on these critical topics, you can ensure that you are well-prepared to tackle any question presented.
Understanding Geometric Proofs and Theorems
At the heart of mathematics, particularly in spatial reasoning, lies the ability to construct and understand logical arguments. These arguments, built on axioms and previously proven facts, form the basis for demonstrating the truth of various relationships between figures. Being able to follow and develop such logical sequences is critical for success in this area.
The Structure of a Proof
A mathematical proof is a step-by-step process that demonstrates the validity of a statement using established principles. Each step relies on previously proven facts or accepted rules. Whether it involves proving congruence between shapes or demonstrating the properties of angles, understanding the structure of a proof is essential. Recognizing the role of each step helps to better grasp how to approach problems that require logical deductions.
Common Theorems and Their Applications
Many theorems are foundational to solving problems efficiently. Theorems like the Pythagorean theorem, properties of parallel lines, and the angle sum of triangles are frequently applied to real-world situations. Familiarity with these theorems allows for quicker problem-solving and helps to establish clear reasoning in proofs. Understanding when and how to apply these key principles can significantly enhance performance when faced with more complex tasks.
How to Approach Geometry Word Problems

Word problems require more than just applying formulas–they challenge you to translate real-world scenarios into mathematical expressions. To solve these types of problems effectively, it’s crucial to break down the given information and identify the relationships between different elements. A clear approach can turn a seemingly complex question into a manageable task.
Start by carefully reading the problem, highlighting important details such as measurements, shapes, and relationships. Next, visualize the situation with a diagram or sketch, which often helps to make abstract concepts clearer. Once the problem is visualized, translate the conditions into mathematical expressions and determine the appropriate formula or theorem to apply. By following this logical progression, you’ll increase your accuracy and efficiency in solving word problems.
Important Formulas to Memorize
Mastering key formulas is essential to efficiently solving problems in mathematics. These expressions provide the foundation for calculating various attributes of shapes and figures, allowing you to quickly find solutions without relying on lengthy derivations. Memorizing and understanding these formulas is a crucial step in developing mathematical proficiency.
Essential Mathematical Expressions
Below is a list of fundamental formulas that are commonly used in solving problems involving different types of shapes and measurements. Familiarizing yourself with these will help you approach tasks with confidence.
| Shape | Formula | Explanation |
|---|---|---|
| Circle | Area = πr² | Used to calculate the area of a circle, where ‘r’ is the radius. |
| Rectangle | Area = l × w | Used to find the area of a rectangle, where ‘l’ is length and ‘w’ is width. |
| Triangle | Area = ½ × b × h | Used to calculate the area of a triangle, where ‘b’ is the base and ‘h’ is the height. |
| Right Triangle | Hypotenuse² = a² + b² | Used to find the length of the hypotenuse in a right triangle, based on the other two sides (‘a’ and ‘b’). |
| Rectangle | Perimeter = 2(l + w) | Used to find the perimeter of a rectangle. |
Advanced Formulas for Specific Situations
In addition to basic formulas, there are more complex expressions used in specific scenarios. For example, when working with composite shapes, you may need to calculate the area or volume by breaking the shape into smaller, more manageable parts. Similarly, knowing how to apply the Pythagorean theorem, trigonometric ratios, and other advanced expressions will allow you to tackle a wider range of problems.
Mastering Coordinate Geometry for Exams
Understanding how to work with the coordinate plane is an essential skill for solving problems involving spatial relationships. This branch of mathematics allows you to analyze points, lines, and shapes by using pairs of numbers that represent locations on a plane. Mastery of these concepts is crucial for efficiently solving a variety of questions, from finding distances to calculating slopes and equations of lines.
To excel in this area, it’s important to become familiar with key principles such as the distance formula, slope calculations, and the equation of a line. These tools enable you to determine the relationship between points and shapes in a two-dimensional space. Practicing these calculations will improve your ability to work with more complex problems, including those that involve transformations and intersections of lines.
Key Formulas to Remember:
- Distance Formula: d = √((x₂ – x₁)² + (y₂ – y₁)²) – This formula is used to find the distance between two points on the coordinate plane.
- Slope Formula: m = (y₂ – y₁) / (x₂ – x₁) – This formula helps calculate the slope of a line between two points.
- Equation of a Line: y – y₁ = m(x – x₁) – This formula represents the equation of a line in point-slope form.
With practice, applying these formulas will become second nature, and you’ll be able to solve problems more efficiently. Recognizing patterns and understanding how these formulas relate to real-world situations will enhance both your speed and accuracy when tackling questions involving the coordinate plane.
Tips for Solving Angle Problems
Solving problems related to angles requires a solid understanding of how different types of angles interact within geometric shapes. From straight lines to complex polygons, each scenario has its own set of rules that govern the relationships between angles. By following a methodical approach and applying the right principles, you can tackle these problems with confidence.
Understanding Angle Relationships
One of the first steps in solving angle-related problems is recognizing the different types of angle relationships. Complementary angles add up to 90°, supplementary angles add up to 180°, and vertical angles are always equal. Being familiar with these relationships allows you to simplify complex problems and find solutions more efficiently. Always start by identifying any known angles and looking for opportunities to apply these relationships.
Using Algebra to Solve for Unknown Angles
In many cases, you’ll need to use algebraic methods to solve for unknown angles. By setting up equations based on angle relationships, you can find the missing values. For example, if two angles are supplementary and one is unknown, you can subtract the known angle from 180° to find the value of the missing angle. Practice working with these types of equations to build confidence in solving angle problems quickly.
Key Strategies:
- Look for parallel lines: Parallel lines create angles with consistent relationships, such as alternate interior or corresponding angles.
- Use the angle sum property: The sum of interior angles in a triangle is always 180°, which can help solve for missing angles in triangular shapes.
By applying these strategies and practicing regularly, you’ll be able to solve angle problems more efficiently and with greater accuracy, making your problem-solving approach more effective overall.
Strategies for Working with Triangles
Triangles are a fundamental shape in mathematics and are often the basis for many problems. Whether dealing with right triangles, isosceles triangles, or equilateral triangles, having a clear approach can simplify the process of solving for unknowns. The key is to understand the properties that make triangles unique and use the right methods to find missing angles or side lengths.
Key Triangle Properties
Before diving into solving problems, it’s essential to understand the properties that apply to different types of triangles. These properties serve as a foundation for most problems involving triangles.
- Sum of Angles: The interior angles of any triangle always add up to 180°.
- Side Relationships: In a right triangle, the Pythagorean theorem can be used to find unknown sides.
- Equal Sides and Angles: In isosceles triangles, two sides are equal, and the angles opposite these sides are also equal.
Solving Triangle Problems Efficiently
To solve problems involving triangles, apply these strategies to make the process easier and more efficient.
- Use the Pythagorean Theorem: For right triangles, use the formula a² + b² = c² to find missing side lengths.
- Apply the Law of Sines or Cosines: For non-right triangles, these laws help find unknown angles or sides when certain information is provided.
- Look for Similarity: Similar triangles have the same shape but different sizes, which allows for proportional relationships between corresponding sides.
- Draw Accurate Diagrams: A well-drawn diagram can make it easier to visualize relationships between angles and sides, helping you spot useful information.
By using these strategies and recognizing the type of triangle you’re working with, you can solve a wide variety of problems effectively and with confidence. Triangles may appear in many different forms, but understanding the core principles behind them will make it easier to find the solution.
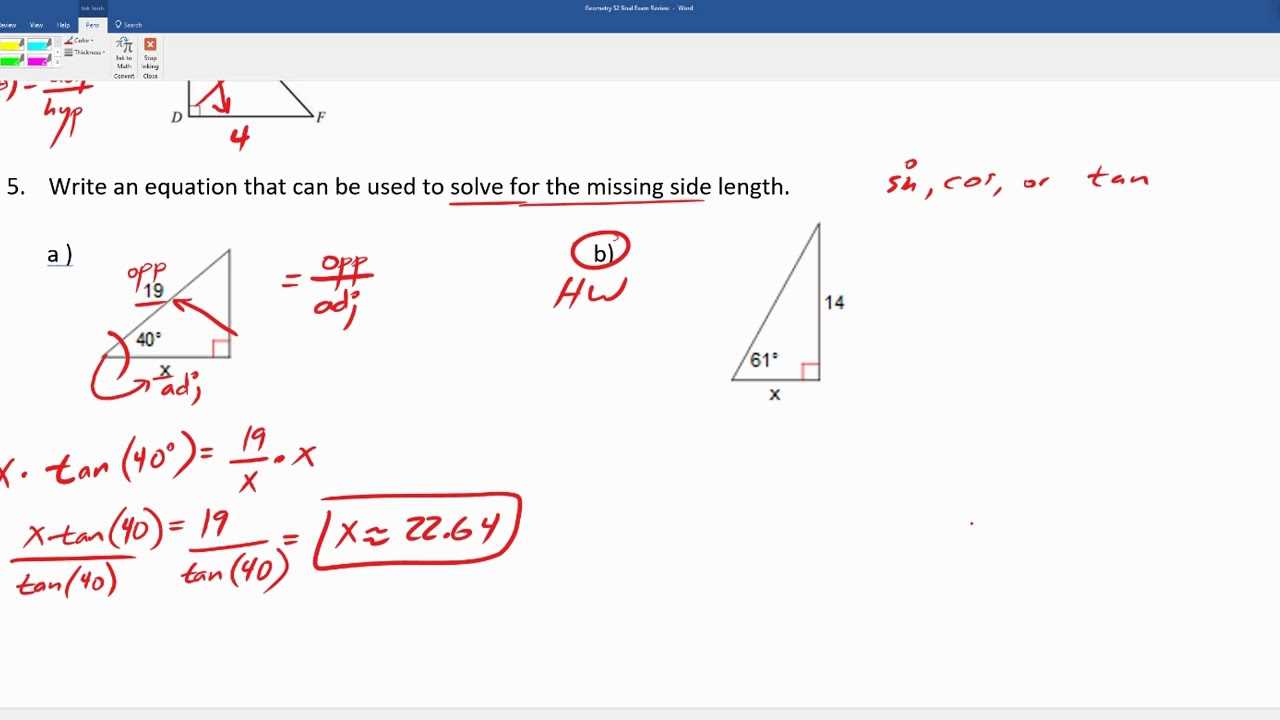
Using Pythagorean Theorem Effectively
The Pythagorean theorem is one of the most widely used principles in mathematics when dealing with right-angled triangles. This fundamental rule helps you relate the lengths of the sides of a triangle, making it invaluable in various problem-solving scenarios. Whether you’re tasked with finding the length of an unknown side or verifying if a triangle is a right triangle, mastering this theorem can significantly improve your efficiency in tackling related problems.
To apply the theorem correctly, it’s important to recognize the parts of the right triangle: the hypotenuse (the longest side, opposite the right angle) and the two legs (the shorter sides). The Pythagorean theorem states that the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the two legs. This simple relationship can be rearranged to solve for any of the three side lengths.
Formula and Application
The formula for the Pythagorean theorem is:
a² + b² = c²
Where:
- a and b: The lengths of the two legs of the right triangle.
- c: The length of the hypotenuse.
By plugging in the known values for the legs or the hypotenuse, you can easily calculate the missing side. In more complex problems, this theorem can be used to check if a triangle is a right triangle by verifying that the sides satisfy the equation.
Example Problem

Consider a right triangle with legs measuring 3 and 4 units. To find the length of the hypotenuse:
| Step | Action | Result |
|---|---|---|
| Step 1 | Apply the Pythagorean theorem | a² + b² = c² |
| Step 2 | Plug in the values for a and b | 3² + 4² = c² |
| Step 3 | Calculate the squares | 9 + 16 = c² |
| Step 4 | Solve for c | 25 = c² |
| Step 5 | Find the square root | c = 5 |
Therefore, the length of the hypotenuse is 5 units. This simple but powerful method can be used to solve countless problems involving right triangles, making it a crucial tool in any mathematical toolkit.
Exploring Circles and Their Properties
Circles are one of the most fundamental shapes in mathematics, found in various real-world applications from engineering to design. Understanding their properties allows for solving numerous problems involving measurements, areas, and angles. Circles are defined by their continuous curves and symmetrical structure, with many important features that simplify calculations and geometric relationships. Knowing these key elements is essential when approaching problems involving circular shapes.
The most important property of a circle is its radius, which is the distance from the center to any point on the circle’s edge. This measurement is crucial in determining other characteristics such as circumference, area, and sector lengths. The diameter, which is twice the length of the radius, is another important element that comes into play when calculating the circle’s properties. These attributes form the basis for many geometric problems involving circles.
Key Formulas for Circles

To effectively work with circles, it’s essential to understand and memorize the key formulas associated with them:
- Circumference: The total distance around the circle is calculated by the formula C = 2πr, where r is the radius of the circle.
- Area: The area inside the circle is given by the formula A = πr², where r is the radius.
- Diameter: The diameter of the circle is simply d = 2r, where r is the radius.
These formulas provide the necessary tools for calculating different aspects of a circle and are applicable in both theoretical and practical scenarios. Understanding the relationships between radius, diameter, and circumference is key to solving problems that involve circular shapes.
Special Properties and Relationships
Circles have several special properties that are important when working with them in more advanced problems:
- Central Angles: An angle formed by two radii of the circle is known as a central angle. The measure of the central angle is directly related to the arc it subtends.
- Chord Properties: A chord is a line segment joining two points on the circle. The perpendicular bisector of a chord always passes through the center of the circle.
- Arc Length: The length of an arc is a fraction of the circle’s circumference, determined by the angle subtended by the arc at the center of the circle.
By exploring these properties and applying the correct formulas, you can solve a variety of problems that involve circles, from finding unknown lengths to calculating areas and angles. Mastering these concepts is an essential part of working with circular shapes in mathematics.
Understanding Area and Volume Calculations

Calculating the space within different shapes is a key concept in mathematics. Whether dealing with flat surfaces or three-dimensional objects, understanding how to find area and volume is essential for solving a wide variety of problems. The process involves applying specific formulas that account for the dimensions of the object or figure in question, allowing you to determine its size in two or three dimensions.
In two-dimensional figures, area refers to the space enclosed by the shape, while volume deals with the amount of space inside three-dimensional objects. Mastering both calculations allows you to solve problems ranging from simple geometric figures to more complex real-world applications like construction, design, and engineering.
Area Calculations
For flat shapes, the area is found by multiplying the relevant dimensions. Each shape has its own specific formula:
- Rectangle: Area = length × width
- Triangle: Area = 1/2 × base × height
- Circle: Area = π × radius²
- Square: Area = side × side
- Parallelogram: Area = base × height
These formulas help you quickly find the area of common two-dimensional shapes. By understanding the structure of each shape and knowing the appropriate formula, you can easily calculate the amount of space enclosed by the figure.
Volume Calculations
For three-dimensional shapes, volume measures the amount of space inside the object. Each shape requires a different formula to determine its volume:
- Cube: Volume = side³
- Rectangular Prism: Volume = length × width × height
- Cylinder: Volume = π × radius² × height
- Sphere: Volume = 4/3 × π × radius³
- Pyramid: Volume = 1/3 × base area × height
By applying the right formula for the shape in question, you can calculate how much space the object occupies. These formulas are critical for a range of fields, including architecture, engineering, and any other discipline where understanding the space taken up by an object is important.
Tips for Geometry Test Time Management
Efficiently managing your time during a mathematical assessment is key to performing well. Balancing the number of questions, the time available, and the difficulty level of each task can make the difference between finishing successfully or leaving answers incomplete. With the right strategies, you can approach each problem methodically, ensuring that you allocate sufficient time for both simpler and more complex tasks.
One of the most important factors in time management is knowing how much time to spend on each section of the test. Planning ahead allows you to focus your efforts and avoid spending too long on any one question. Prioritizing tasks based on familiarity and difficulty can also help you stay organized and efficient throughout the entire assessment.
1. Prioritize Easy Questions
Start by tackling questions that you feel most comfortable with. These are typically the ones that will take the least amount of time and will help you build confidence. By finishing easier questions first, you’ll gain momentum and ensure that you don’t run out of time for the simpler problems.
2. Allocate Time for Difficult Problems
Set aside a specific amount of time for the more challenging questions. If you find yourself stuck on a problem, don’t waste valuable minutes trying to solve it. Instead, move on and come back to it later if time allows. This strategy helps prevent frustration and keeps your overall pace steady.
3. Use a Timer
Many people find it helpful to break the test into segments by using a timer. Set a specific time limit for each section or question type, and keep track of how much time remains. This practice will help you stay on schedule and avoid spending too much time on any one part of the test.
4. Don’t Forget to Review
If time permits, always leave a few minutes at the end of the assessment for reviewing your answers. Double-check for errors or missed steps, especially in problems that require detailed calculations or multi-step reasoning. Reviewing ensures that you catch mistakes and gives you a chance to improve your final score.
Common Mistakes to Avoid in Geometry
When working with mathematical concepts that involve shapes, measurements, and properties, it’s easy to fall into traps that can lead to errors. Even the most experienced individuals can make simple mistakes if they are not careful. Identifying and avoiding these common pitfalls can significantly improve your performance and understanding. Below are some of the most frequent mistakes and tips on how to avoid them.
1. Misinterpreting Problem Statements
Often, problems include important details that are easy to overlook or misunderstand. Whether it’s a given value, a condition, or a relationship between elements, misreading the question can lead to incorrect solutions. Here are some ways to avoid this:
- Read the problem thoroughly before attempting to solve it.
- Highlight or underline key information provided in the question.
- Rephrase the problem in your own words to ensure full comprehension.
2. Forgetting to Apply Theorems or Properties
Mathematical problems often require specific principles or rules to be applied, such as theorems, formulas, or properties of shapes. Missing these essential steps can result in incomplete or inaccurate solutions. To prevent this mistake:
- Keep a list of key principles and formulas handy for reference.
- Ensure you understand which theorems are relevant to each type of problem.
- Double-check your work to make sure you’ve used the correct properties.
3. Incorrectly Using Units of Measurement
In many problems, measurements are given in various units, and converting between them may be necessary. Failing to convert units correctly can lead to errors in calculations. To avoid this mistake:
- Always check that the units of measurement match what is required in the solution.
- Use conversion factors when needed to ensure consistency.
- Be mindful of square and cubic units when working with area or volume.
4. Overlooking Symmetry
Symmetry plays a crucial role in simplifying problems involving shapes. Ignoring symmetrical properties or failing to recognize them can complicate the solution process. To avoid this, try the following:
- Look for any symmetrical features in the figure that could simplify calculations.
- Divide complex shapes into symmetrical parts to make problem-solving easier.
- Always check if the problem mentions symmetry or if it’s implied by the shape.
5. Rushing Through Calculations
Speeding through calculations in an attempt to finish quickly can lead to careless mistakes. Double-checking your math can prevent minor errors from snowballing into bigger problems. To minimize these mistakes:
- Work at a steady pace, focusing on accuracy rather than speed.
- Revisit key steps if you’re unsure of your calculation.
- Check your final answer to ensure it makes sense in the context of the problem.
By being aware of these common mistakes and applying strategies to avoid them, you’ll be better equipped to handle problems with confidence and accuracy.
How to Prepare for Geometry Word Problems
Word problems can be challenging, especially when they involve applying mathematical concepts to real-world situations. To tackle these types of questions effectively, it’s important to approach them with a clear strategy. By breaking down the problem, identifying relevant information, and systematically applying principles, you can significantly improve your ability to solve word problems with confidence.
1. Understand the Problem and Identify Key Information
The first step in solving any word problem is to carefully read the question and fully understand what is being asked. Look for key details that will help you set up your solution, such as measurements, relationships, or conditions. You can:
- Underline or highlight important information.
- Write down the given values and unknowns in the problem.
- Restate the problem in your own words to ensure comprehension.
2. Translate the Words into Mathematical Expressions
Once you have a clear understanding of the problem, the next step is to translate the written information into mathematical expressions. Many word problems can be solved by applying formulas, theorems, or other mathematical tools. To do this:
- Identify the type of problem you are dealing with (e.g., area, perimeter, volume).
- Set up equations based on the relationships described in the problem.
- Substitute the known values into the appropriate formulas.
By taking these initial steps, you will set yourself up for a successful approach to solving any word problem. The key is to stay organized, follow a logical sequence, and practice regularly to sharpen your skills.
Practicing Geometry Problems with Examples

Regular practice is one of the most effective ways to solidify your understanding of mathematical concepts. By working through a variety of problems and examples, you can develop a deeper insight into how different principles apply in different scenarios. This section will guide you through a structured approach to practicing problems, helping you to build confidence and improve your problem-solving skills.
1. Start with Simple Examples
When you’re first learning a concept, it’s important to start with easier problems before tackling more complex ones. Simple problems allow you to get comfortable with the basic steps and formulas involved. Focus on:
- Identifying the basic shapes and figures.
- Applying simple calculations, such as finding the area or perimeter.
- Understanding the relationships between the elements of the problem.
2. Progress to More Complex Scenarios
Once you’re comfortable with the basics, it’s time to challenge yourself with more difficult examples. These problems often involve multiple steps or require the application of several different concepts. When practicing more complex problems:
- Break down the problem into smaller, manageable parts.
- Look for patterns or similarities to problems you’ve solved before.
- Be patient and take time to check your work as you go.
By consistently practicing problems, you will gain a better understanding of how to apply different strategies and improve your efficiency in solving similar problems in the future.
Final Preparation Checklist
Preparing for an important assessment can feel overwhelming, but a well-organized checklist can help ensure that you’re ready for the challenges ahead. By breaking down your preparation into smaller, actionable tasks, you can approach the process with confidence and clarity. This checklist will guide you through the final steps to make sure you’re fully prepared and ready to perform at your best.
1. Review Key Concepts
Make sure you have a solid understanding of the core principles. Focus on:
- Revisiting essential formulas and their applications.
- Identifying common problem types and practice solving them.
- Reviewing past lessons to reinforce concepts that are crucial for the assessment.
2. Practice Under Time Constraints
One of the best ways to prepare for a timed assessment is to simulate the actual testing conditions. To do this:
- Set a timer and solve practice problems within the designated time limit.
- Work on pacing to ensure you can complete all questions in the given time frame.
- Analyze any mistakes or challenges faced during timed practice to avoid repeating them.
By following this checklist and making consistent progress each day, you can improve both your skills and your confidence as the assessment approaches.