Core Connections Algebra 1 Chapter 8 Answers

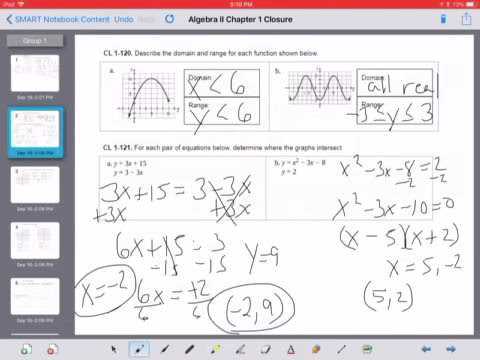
In this section, we delve into essential mathematical principles that serve as the foundation for more complex topics. Through careful exploration and problem-solving, learners will gain a deeper understanding of various concepts and develop the skills necessary to tackle advanced challenges. By approaching each problem step by step, students can build confidence and mastery over time.

The focus is on applying critical thinking to solve equations, interpret functions, and analyze relationships between different mathematical elements. Mastering these skills not only improves problem-solving abilities but also prepares students for future studies in related fields. With clear explanations and practical examples, this section aims to guide learners through the process of achieving proficiency in the subject.

As we work through each example, you’ll discover effective methods to simplify complex ideas, making them accessible and understandable. By reinforcing these core skills, you will be better equipped to handle a variety of mathematical challenges with ease and confidence.

Core Connections Algebra 1 Chapter 8 Solutions

This section explores the key problems and solutions that students encounter while working through this mathematical unit. The focus is on providing clear, structured solutions that can help learners understand the underlying principles behind each problem. Whether tackling equations, inequalities, or functions, the goal is to simplify complex concepts into manageable steps.

Each solution is broken down to show the logical process behind it, guiding students through the thought process involved in reaching the correct conclusion. This approach ensures that learners not only find the right answers but also develop the skills needed to solve similar problems independently in the future.

The solutions presented here cover a wide range of topics, including:

• Solving linear equations and inequalities
• Graphing functions and interpreting their behavior
• Applying operations with polynomials and rational expressions
• Understanding systems of equations and methods for solving them

By examining each solution in detail, students can gain a comprehensive understanding of how to approach these types of problems, laying the groundwork for more advanced topics. These examples provide a valuable resource for reinforcing key skills and mastering the content in a structured, clear way.

Understanding the Approach to Mathematical Mastery

This approach focuses on developing a deep understanding of mathematical concepts through structured learning. By breaking down complex problems into smaller, more manageable steps, students are able to build a solid foundation of knowledge that prepares them for more advanced topics. The key to this method is active engagement, where learners not only memorize formulas but also understand the reasoning behind each mathematical principle.

The Importance of Conceptual Understanding

Rather than simply focusing on rote memorization, this method emphasizes the importance of grasping underlying concepts. Students are encouraged to make connections between different mathematical ideas, fostering a deeper, more lasting understanding. This helps them approach problems with confidence and creativity, knowing how to apply learned concepts in varied situations.

Building Skills through Practice

In this approach, consistent practice is crucial. By working through a wide variety of problems, students can reinforce their understanding and improve their problem-solving abilities. This hands-on experience allows them to experiment with different strategies, ultimately finding the most efficient methods for solving complex problems.

Stage	Objective	Key Focus
Initial Exposure	Introduce new concepts	Understanding basic principles
Practice Phase	Reinforce concepts through exercises	Application of learned skills
Advanced Problem Solving	Apply knowledge to complex scenarios	Critical thinking and reasoning

By following this structured approach, students develop not just the ability to solve mathematical problems, but also the skills to think critically and creatively in any mathematical context.

Key Concepts Covered in Chapter 8

This section introduces several important mathematical principles that serve as the foundation for solving more complex problems. The focus is on understanding the relationships between different elements of mathematics, including expressions, equations, and functions. Each concept builds upon the last, creating a coherent structure that allows students to apply learned techniques to solve a variety of problems effectively.

Among the main topics explored are:

• Operations with linear expressions and equations
• Solving inequalities and understanding their graphs
• Exploring the properties and behaviors of functions
• Techniques for simplifying and manipulating polynomials
• Methods for solving systems of equations

By mastering these key ideas, students can develop a well-rounded understanding of the subject, enabling them to solve problems with greater ease and confidence. Each concept is designed to reinforce mathematical thinking and promote deeper comprehension, ensuring that students are fully equipped to tackle future challenges.

Step-by-Step Solutions for Each Problem

This section provides detailed, methodical explanations for solving various problems found within the unit. Each solution is broken down into individual steps, allowing students to follow the process from start to finish. The goal is to ensure that learners can understand the logic behind every move, making it easier to apply the same strategies to other problems.

By outlining each procedure clearly, students gain insight into how to approach similar challenges. Each solution emphasizes critical thinking and careful analysis, helping learners to develop the skills necessary for solving complex mathematical tasks. These step-by-step guides serve as valuable tools for reinforcing understanding and building confidence in problem-solving techniques.

Breaking Down Complex Algebraic Expressions

In this section, we focus on simplifying and understanding complex mathematical formulas by breaking them down into smaller, more manageable parts. By carefully analyzing each element within an expression, students can gain a clearer understanding of how to manipulate and solve them efficiently. This process involves identifying like terms, applying distributive properties, and simplifying step by step.

Here are the key strategies for simplifying complex expressions:

• Combine like terms to reduce the expression to its simplest form
• Use the distributive property to expand or factor expressions
• Apply rules of exponents when necessary
• Rearrange terms to make the expression easier to work with

By mastering these techniques, students can tackle increasingly complex equations with confidence. This methodical approach not only helps in solving problems but also reinforces the underlying mathematical principles involved in each operation.

How to Approach Word Problems Effectively

Word problems often present challenges because they require both interpreting the situation described and translating it into mathematical expressions. To solve them successfully, it’s essential to break down the information provided and systematically translate it into an equation or set of equations. By following a structured approach, students can more easily identify key information and find the solution step by step.

Here are some effective steps to approach word problems:

• Read the problem carefully and identify what is being asked.
• Highlight or underline key numbers, operations, and conditions.
• Define variables to represent unknown values.
• Translate the word problem into a mathematical equation or system of equations.
• Solve the equation using appropriate methods and check the solution for consistency with the problem’s context.

By following this method, students can break down even the most complex word problems into manageable steps. With practice, interpreting and solving word problems becomes a skill that enhances overall mathematical reasoning and problem-solving ability.

Common Mistakes to Avoid in Algebra 1

While learning mathematical concepts, it’s easy to make mistakes, especially when dealing with complex operations and abstract concepts. Identifying and understanding these common errors is essential for improving problem-solving skills. By recognizing where students often go wrong, learners can avoid pitfalls and develop a more effective approach to solving mathematical problems.

Some frequent mistakes include misinterpreting the question, forgetting to apply proper rules, or making errors during calculations. These mistakes can lead to incorrect answers, but with practice and awareness, they can be minimized.

Mistake	Explanation	How to Avoid It
Misunderstanding the problem	Overlooking key information or misinterpreting the wording	Carefully read the problem, underline key terms, and restate it in simpler words
Incorrectly applying the distributive property	Forgetting to multiply all terms in parentheses	Double-check each step when distributing to ensure all terms are included
Sign errors in equations	Confusing positive and negative signs, especially in subtraction	Pay extra attention to signs, and when in doubt, rewrite the expression
Dividing by zero	Dividing any number by zero results in an undefined expression	Always check the denominator to ensure it’s not zero
Skipping steps in solving equations	Jumping ahead without properly simplifying or isolating variables	Follow each step methodically to avoid skipping important parts of the process

By paying attention to these common mistakes, students can refine their problem-solving techniques and build a stronger foundation for tackling more advanced topics.

Tips for Improving Problem-Solving Skills

Developing strong problem-solving skills is essential for success in mathematics. It involves more than just memorizing formulas–it requires critical thinking, creativity, and persistence. With practice and the right strategies, anyone can enhance their ability to solve complex problems efficiently and effectively.

Here are some valuable tips for improving your problem-solving abilities:

• Understand the problem: Carefully read the question and identify what is being asked. Break it down into smaller, more manageable parts.
• Develop a plan: Once you understand the problem, plan your approach. Decide which methods or formulas to apply, and think through the steps required to solve it.
• Work through examples: Practice by working through similar problems. This will reinforce your understanding and provide insight into the most effective strategies.
• Check your work: After solving a problem, always review your solution to ensure it makes sense. Verify your calculations and reasoning to catch any potential mistakes.
• Stay persistent: If you’re stuck, don’t give up. Take a break, then return to the problem with a fresh perspective. Sometimes stepping away can help clarify things.
• Ask for help: If you’re struggling with a concept, seek assistance from a teacher, tutor, or peer. Collaboration often provides new insights and approaches.

By incorporating these strategies into your learning routine, you can gradually improve your problem-solving skills and gain confidence in tackling even the most challenging problems.

Using Visual Aids to Understand Algebra

Visual aids are powerful tools that can help students better understand complex mathematical concepts. By turning abstract problems into visual representations, learners can grasp relationships, patterns, and operations more easily. Whether it’s graphs, diagrams, or charts, visual aids simplify the learning process and make abstract ideas more concrete.

Here are some examples of how visual tools can enhance understanding:

• Graphs: Plotting equations on a graph can help students see the relationship between variables and understand concepts like slope, intercepts, and linearity.
• Diagrams: Using diagrams to represent problems, such as geometric shapes or number lines, can clarify difficult concepts and help with spatial reasoning.
• Tables: Organizing data or equations in tables allows students to observe patterns and relationships between numbers more clearly.
• Color-coded steps: Highlighting different steps or terms in different colors helps visually distinguish components of a problem, making it easier to follow through each part of the solution.

By incorporating visual aids into your study routine, you can make abstract concepts more accessible and improve problem-solving efficiency. These tools help transform challenging problems into understandable, manageable pieces, leading to greater clarity and confidence in your learning journey.

Real-World Applications of Algebra Concepts

Mathematical principles are not just abstract concepts–they have real-world applications that are essential in a variety of fields. Understanding how to apply mathematical operations and equations can help solve practical problems in everyday life, as well as in careers such as engineering, economics, and science. These concepts can be used to model situations, predict outcomes, and make informed decisions.

For instance, algebra is commonly used in:

• Finance: Understanding interest rates, loan payments, and investment growth involves using equations to calculate profits and costs over time.
• Engineering: Engineers use mathematical equations to design structures, calculate forces, and determine dimensions of materials in construction.
• Technology: Computer programming often involves solving equations to optimize software performance or process large datasets.
• Healthcare: Medical professionals use mathematical models to analyze data, such as predicting the spread of diseases or calculating medication dosages.
• Sports: Analysts use statistics and algebraic models to evaluate player performance, predict game outcomes, and optimize team strategies.

By understanding how these concepts work in practical applications, students can see the value of their studies and how math influences the world around them. These real-world uses of mathematics demonstrate how abstract ideas translate into tangible results in various industries and daily activities.

Strategies for Mastering Equations and Inequalities

Solving equations and inequalities is a fundamental skill in mathematics. Whether you’re dealing with simple linear equations or more complex expressions, mastering these techniques is essential for success in higher-level math. The key to solving these problems is understanding the principles behind each type of equation or inequality and applying systematic methods to find solutions.

Here are some strategies to help you excel in solving equations and inequalities:

Understand the Basics

Before attempting to solve problems, make sure you have a solid understanding of the basic operations involved, such as addition, subtraction, multiplication, and division. Mastering these foundational skills will help you manipulate equations more easily.

Apply Step-by-Step Methods

When solving equations and inequalities, it’s important to follow a logical step-by-step approach. Start by isolating the variable, simplifying both sides of the equation, and checking your solution at each stage.

Step	Action
Step 1	Isolate the variable on one side of the equation.
Step 2	Simplify both sides of the equation (combine like terms).
Step 3	Solve for the variable by performing inverse operations.
Step 4	Check the solution by substituting the value back into the original equation.

For inequalities, remember to reverse the inequality symbol when multiplying or dividing both sides by a negative number. This is a common mistake, so be cautious when working with negative values.

By practicing these methods consistently and approaching each problem methodically, you’ll develop the skills needed to solve equations and inequalities accurately and confidently.

Exploring Functions and Their Graphs

Functions are a fundamental concept in mathematics that describe relationships between variables. By understanding how one quantity affects another, we can create models that predict outcomes and explain patterns in various fields such as physics, economics, and engineering. The graph of a function visually represents this relationship, providing insights into how the variables interact.

Here are some key aspects of exploring functions and their graphs:

• Understanding the domain and range: The domain refers to the set of input values, while the range represents the corresponding output values. Analyzing these can help identify valid values for which the function is defined.
• Identifying function types: Functions can be classified into various types, such as linear, quadratic, exponential, and polynomial. Each type has unique properties that affect its graph.
• Plotting points: To graph a function, we plot pairs of input and output values on a coordinate plane. The resulting points form a curve or line that represents the function.
• Understanding slopes and intercepts: In linear functions, the slope indicates the rate of change, while the intercepts show where the graph crosses the axes. These values are key to interpreting the function’s behavior.
• Transformations of graphs: Functions can be shifted, stretched, or reflected on the graph. Understanding how to apply these transformations helps modify graphs to represent different situations or constraints.

By learning how to analyze and interpret the graphs of functions, you can gain a deeper understanding of how mathematical relationships operate and how they are used to model real-world phenomena. Whether you’re solving problems in science, economics, or engineering, mastering these concepts will enhance your problem-solving skills and allow you to apply mathematical thinking in practical ways.

How to Check Your Answers for Accuracy

Verifying the correctness of your solutions is an essential step in solving mathematical problems. Whether you are working with equations, inequalities, or other types of problems, ensuring that your answer is accurate helps avoid mistakes and reinforces your understanding of the material. There are several methods you can use to check your work and confirm that your solution is correct.

Here are some effective strategies to verify your results:

• Substitute the solution back into the original problem: One of the simplest ways to check your solution is by substituting it back into the original equation or expression. If both sides of the equation are equal, your solution is correct.
• Use a different method to solve the problem: If possible, solve the problem using an alternate method to verify the answer. For example, if you solved an equation algebraically, try solving it graphically or numerically to see if the results match.
• Estimate the solution: If the problem involves numbers, estimating the solution can be a quick way to check for obvious errors. Compare your result to the estimate–if the numbers are far apart, there may be a mistake.
• Check for consistency in your work: Review the steps you took to arrive at your answer. Ensure that you didn’t skip any steps, and verify that each operation was performed correctly. Look for common errors, such as sign mistakes or arithmetic errors.
• Use a calculator or software tool: When applicable, use a calculator or a software tool to check your results. These tools can provide quick and accurate solutions, helping you spot any discrepancies in your calculations.

By regularly checking your work, you can build confidence in your problem-solving abilities and ensure that your solutions are reliable. These verification techniques not only help you catch mistakes but also deepen your understanding of the underlying concepts, making future problems easier to solve.

Key Vocabulary from Chapter 8

Understanding the terminology is an essential part of mastering any subject, especially when it comes to solving mathematical problems. In this section, we will explore the key terms and concepts that are crucial for understanding the material covered. These words will help build a foundation for solving more complex problems and deepen your comprehension of the topic.

Important Terms to Remember

• Expression: A mathematical phrase that combines numbers, variables, and operations but does not include an equal sign.
• Equation: A statement that asserts the equality of two expressions, typically containing an equal sign (=).
• Variable: A symbol, usually a letter, that represents a number in an equation or expression.
• Coefficient: A number that multiplies a variable in an expression or equation.
• Constant: A fixed value in an equation or expression that does not change.
• Solution: The value or set of values that satisfies an equation or inequality.

Concepts to Clarify

• Linear Equation: An equation that represents a straight line when graphed, typically written in the form Ax + B = C.
• Inequality: A mathematical statement that compares two expressions using inequality symbols such as >, <, ≥, or ≤.
• Graph: A visual representation of an equation or inequality on a coordinate plane.
• Intercept: The point where a graph crosses the x-axis or y-axis.

Mastering these terms is vital for progressing in problem-solving. By becoming familiar with this vocabulary, students can better understand problems, recognize key patterns, and apply the right methods to arrive at correct solutions.

Practice Exercises for Reinforcement

Reinforcement through practice is one of the most effective ways to strengthen your understanding of mathematical concepts. The exercises in this section are designed to help solidify key skills and ensure that the techniques learned are applied accurately. By solving these problems, you will reinforce your problem-solving abilities and build confidence in approaching more complex challenges.

It’s important to practice a variety of problems, from basic to more advanced, to fully grasp the range of concepts. Each exercise targets a specific skill and is meant to encourage critical thinking and the ability to solve equations and inequalities efficiently. As you work through these problems, remember that consistency and attention to detail are key to mastering the material.

• Solve simple linear equations involving one variable.
• Graph the solution to inequalities on a coordinate plane.
• Factor expressions and simplify them where possible.
• Identify the slope and y-intercept from given equations.
• Translate word problems into algebraic equations.
• Work through multi-step problems that require the application of different techniques.

Completing these exercises will not only help you understand the concepts more deeply but also improve your speed and accuracy when solving problems. Make sure to review your solutions carefully to identify any mistakes and understand the reasoning behind the correct approach.

Additional Resources for Algebra 1 Success

While practicing problems is crucial, supplementary resources can also play a significant role in boosting your understanding and mastery of key mathematical concepts. Utilizing various study materials, online tools, and support from peers or tutors can provide different perspectives and reinforce what you’ve learned. This section highlights a variety of resources that can complement your efforts and enhance your problem-solving skills.

Online Tools and Websites

There are several websites that offer free practice problems, video tutorials, and interactive exercises. These platforms allow you to work through problems at your own pace while providing immediate feedback on your solutions. Here are some valuable online resources:

Website	Resource Type	Features
Khan Academy	Videos & Practice	Comprehensive lessons and quizzes on various topics with step-by-step explanations.
IXL	Interactive Exercises	Personalized learning plan with immediate feedback on exercises.
Wolfram Alpha	Problem Solver	Powerful computational tool for solving equations, graphing, and detailed explanations.
PatrickJMT	Video Tutorials	Clear, concise math tutorials for understanding complex problems and solutions.

Study Groups and Tutoring

Engaging with study groups or seeking personalized tutoring can significantly enhance your understanding. Collaborative learning allows you to discuss complex topics, share different problem-solving strategies, and clarify doubts. Whether through online platforms or in-person sessions, tutoring provides a more tailored approach to your learning. Here are some ways to find additional help:

• Join a study group in your class or online community where you can ask questions and solve problems together.
• Consider finding a tutor who can offer one-on-one support and focus on your specific areas of difficulty.
• Participate in online forums such as Stack Exchange, where you can get help from experts and fellow learners.

By utilizing these resources, you can gain a deeper understanding of the material and improve your problem-solving skills. Whether you’re reviewing core concepts, solving practice problems, or looking for in-depth explanations, the combination of online tools and personalized support will help guide you to success.