
Understanding the fundamental principles of shapes, angles, and their relationships is key to advancing in mathematics. In this section, we will explore critical topics that form the backbone of many mathematical problems. The focus will be on unraveling the core elements that help in solving practical and theoretical questions.
Clear understanding of key techniques and methods is crucial for applying them correctly in various scenarios. This section covers a wide range of ideas, from calculating areas to interpreting geometric figures, and offers guidance on how to solve complex exercises efficiently.
By breaking down the problems step-by-step, we aim to build a solid foundation that makes tackling more advanced topics easier. With the right approach, mastering these concepts will not only improve problem-solving skills but also boost confidence in handling mathematical challenges.
Geometry Chapter 7 Review Answers

In this section, we dive into key concepts that are essential for solving problems related to shapes, measurements, and spatial relationships. These foundational ideas not only support the understanding of complex scenarios but also lay the groundwork for future mathematical exploration.
By examining the relationships between various elements, such as angles, sides, and proportions, you can improve your ability to approach and solve different types of questions. Each problem has its own unique set of steps, which, when followed correctly, lead to accurate results.
With a clear approach to tackling exercises and a focus on understanding the underlying principles, mastering this material becomes a logical progression. Whether calculating areas or solving for unknown values, honing these techniques enhances both accuracy and efficiency in problem-solving.
Key Concepts in Geometry Chapter 7
Understanding the fundamental principles behind shapes, angles, and their interrelations is crucial for solving various mathematical challenges. This section focuses on the core ideas that are essential for working with geometric figures and measurements, providing a solid foundation for tackling complex problems.
Basic principles such as the properties of different shapes, the relationship between angles, and the calculation of areas and perimeters are the building blocks for further exploration in this field. Mastering these concepts allows for a deeper understanding of how to approach different types of problems effectively.
In addition to recognizing the characteristics of figures, understanding how to apply theorems and formulas is vital for solving practical and theoretical problems. Critical techniques like finding missing angles or using similarity and congruence principles are tools that will be repeatedly used in future exercises.
Understanding Basic Geometric Shapes
The study of shapes forms the cornerstone of many mathematical problems. Recognizing the key characteristics of various figures is essential for solving a wide range of exercises. These figures come in various forms, each with its own set of properties that help in understanding their behavior and relations with other objects.
Shapes can be classified into categories based on the number of sides, angles, and symmetries they possess. From triangles to quadrilaterals, each type has its distinct features that make it unique. Knowing these properties allows for accurate calculations and problem-solving techniques.
| Shape | Number of Sides | Key Properties |
|---|---|---|
| Triangle | 3 | Sum of angles = 180°, can be equilateral, isosceles, or scalene |
| Square | 4 | All sides equal, all angles 90°, opposite sides parallel |
| Rectangle | 4 | Opposite sides equal, all angles 90° |
| Circle | 0 | No sides, constant radius from center |
By understanding the basic properties of these figures, you can approach more advanced problems with a clearer perspective and stronger problem-solving skills.
Review of Area and Perimeter Formulas
Calculating the area and perimeter of different shapes is a fundamental skill in mathematics. These formulas are essential for determining the space inside various figures and the total distance around them. Knowing how to apply these formulas allows you to solve a wide range of problems involving measurements and spatial relationships.
Formulas for Common Shapes
- Rectangle:
- Area = length × width
- Perimeter = 2 × (length + width)
- Square:
- Area = side²
- Perimeter = 4 × side
- Triangle:
- Area = ½ × base × height
- Perimeter = side₁ + side₂ + side₃
- Circle:
- Area = π × radius²
- Perimeter (Circumference) = 2 × π × radius
Using Formulas in Real-World Scenarios
These formulas are not only theoretical but also have practical applications in real-life situations, such as determining the amount of paint needed for a wall (area) or the length of fencing required for a garden (perimeter). Mastering these calculations ensures accuracy in both everyday tasks and more complex mathematical challenges.
Exploring Angle Relationships in Geometry
Understanding the relationships between angles is essential for solving various problems involving shapes and figures. Angles often interact in specific ways, and knowing these relationships helps simplify calculations and aids in identifying unknown values in geometric problems.
Some angle relationships are fundamental and occur frequently in many types of problems. These relationships help in finding missing angles or understanding the behavior of lines and intersections. For example, complementary and supplementary angles are commonly used in various proofs and calculations.
| Angle Relationship | Description | Example |
|---|---|---|
| Complementary Angles | Two angles that add up to 90° | If one angle is 30°, the other must be 60° |
| Supplementary Angles | Two angles that add up to 180° | If one angle is 120°, the other must be 60° |
| Vertical Angles | Angles formed opposite each other when two lines intersect; they are always equal | If one angle is 45°, the opposite angle is also 45° |
| Adjacent Angles | Two angles that share a common side and vertex | When two angles share a side, they add up to form a larger angle |
These angle relationships form the basis for solving many types of problems. By mastering them, you can tackle more complex geometric concepts with confidence and ease.
Properties of Triangles and Their Sides
Triangles are one of the most fundamental shapes in mathematics, and understanding their properties is crucial for solving a wide range of problems. The relationship between the sides and angles of a triangle plays a significant role in determining its characteristics and helps in deriving important measurements.
Each triangle has specific properties depending on the lengths of its sides and the measures of its angles. These properties help classify triangles into different types, such as equilateral, isosceles, and scalene. Additionally, the rules governing the sum of angles and the relationships between the sides provide useful insights for solving real-world problems.
One of the key concepts is the triangle inequality theorem, which states that the sum of the lengths of any two sides of a triangle must always be greater than the length of the third side. This property is essential when determining whether a set of side lengths can form a valid triangle.
How to Solve for Missing Angles
Finding missing angles is a fundamental skill in solving various types of problems involving shapes. When certain angles are unknown, there are established methods to calculate their values based on the known information. These methods rely on specific relationships and properties between angles, which can help you deduce the unknown values.
One common technique involves using the sum of angles in certain shapes. For example, in any triangle, the sum of the angles is always 180°. By subtracting the known angles from 180°, you can easily find the missing angle. Similarly, when working with other polygons or intersecting lines, there are additional rules and theorems that can help solve for unknown angles.
Another important concept is the use of supplementary and complementary angles. If two angles form a straight line, they are supplementary and add up to 180°. If they form a right angle, they are complementary and sum to 90°. Understanding these relationships allows you to quickly solve for missing angles in many different scenarios.
Application of Theorems in Geometry
Theorems play a crucial role in solving problems and understanding the relationships between various geometric elements. These proven principles are not only essential for theoretical understanding but also for practical problem-solving. By applying theorems, you can derive unknown values and prove properties of shapes with precision.
Various theorems serve as tools for addressing specific challenges. Some are particularly useful for working with angles, while others focus on side lengths, symmetry, or congruency between shapes. Below are some key theorems frequently applied in geometric calculations:
- Pythagorean Theorem: Used to find the length of a side in a right triangle when the lengths of the other two sides are known.
- Angle Sum Theorem: The sum of the angles in any triangle is always 180°.
- Congruence Theorems: Helps determine if two triangles are identical in shape and size based on their sides and angles.
- Similarity Theorems: Used to establish proportional relationships between the sides of similar figures.
- Parallel Line Theorems: Provides relationships between angles when two parallel lines are cut by a transversal.
By mastering these theorems and knowing when to apply them, you can simplify complex problems and find accurate solutions more efficiently. Theorems also serve as the foundation for more advanced mathematical concepts, making them indispensable in the study of shapes and figures.
Step-by-Step Solutions for Problems
Solving problems systematically is key to understanding and mastering any mathematical concept. By breaking down complex tasks into smaller, manageable steps, you can approach each challenge with clarity and precision. Step-by-step solutions help ensure that all necessary calculations and logical steps are followed, leading to accurate results.
To tackle problems effectively, it’s essential to first analyze the given information and identify the unknowns. Once you’ve established what needs to be solved, you can apply relevant formulas, theorems, or properties in a structured manner. Each step should build on the previous one, allowing you to work through the problem logically.
Here’s an example of a step-by-step approach to solving a problem:
- Read the Problem: Understand what is being asked and identify the given values.
- Plan the Solution: Choose the appropriate method or formula to apply.
- Execute the Calculation: Perform the necessary arithmetic or geometric steps to solve for the unknown.
- Check the Work: Verify that the solution makes sense and that all steps are correctly followed.
- Answer the Question: Present the final solution clearly, ensuring it addresses the original problem.
By following these steps for every problem, you can simplify even the most challenging tasks and ensure that your solutions are both accurate and efficient.
Importance of Proofs in Geometry

Proofs are the cornerstone of mathematical reasoning. They provide a logical foundation for establishing the truth of statements and concepts, ensuring that results are not just assumed but verified. In the context of shapes, lines, and angles, proofs help demonstrate why certain relationships hold true and enable the development of further mathematical ideas.
By constructing a proof, you apply established facts, theorems, and logical reasoning to show that a claim is valid. This process not only strengthens your understanding of the subject but also allows for the creation of new theorems and insights that can be applied in a wide range of situations. In essence, proofs are a means of building confidence in the conclusions drawn from mathematical principles.
Logical Structure and Deductive Reasoning
A proof is more than just a series of steps; it is a carefully structured argument. Each step in a proof is based on previously established facts or axioms, which ensures that the conclusion is reliable. Deductive reasoning, which starts with general principles and moves toward specific conclusions, is the key to making a proof valid and convincing.
Building a Strong Foundation for Further Study
Mastering the art of proof construction not only enhances problem-solving skills but also prepares you for more advanced studies in mathematics and related fields. A deep understanding of proofs is crucial for tackling complex concepts and contributes to the development of critical thinking skills that are useful in a variety of disciplines.
Common Mistakes in Chapter 7
When working through problems involving shapes, angles, and other related concepts, it’s easy to make certain errors that can lead to incorrect results. These mistakes are often due to misunderstandings of fundamental principles or rushing through calculations without careful thought. Recognizing and addressing these common errors is essential for mastering the material and achieving accurate solutions.
Many mistakes arise from misapplying formulas, forgetting key relationships, or neglecting to check work before concluding the answer. By being aware of these pitfalls, you can avoid frustration and ensure a deeper understanding of the concepts at hand.
Misinterpreting Problem Conditions
A frequent mistake occurs when the given information in a problem is misinterpreted. This can lead to using the wrong formula or applying the wrong method to solve for the unknowns. It’s crucial to carefully read each problem and identify all relevant details, ensuring that no important condition is overlooked.
Forgetting Key Theorems and Properties
Another common issue is forgetting important theorems or properties that are essential for solving a problem. Many problems rely on the application of specific geometric rules, such as the angle sum property or the Pythagorean theorem. Failing to recall or apply these rules correctly can lead to incorrect results and confusion.
Tips for Mastering Chapter 7
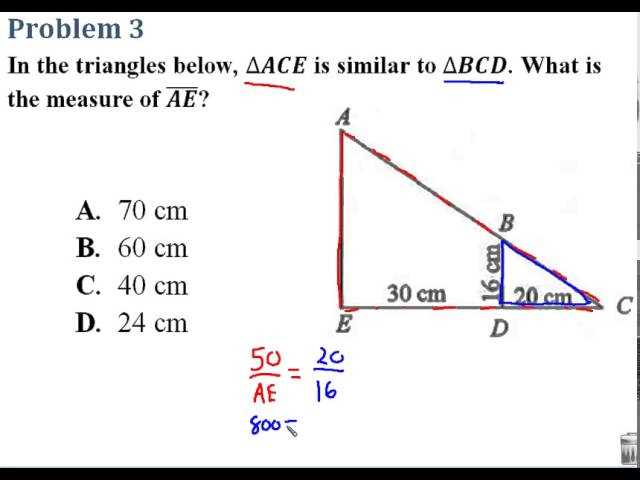
Successfully understanding and applying key concepts in the study of shapes and spatial reasoning requires a combination of practice, comprehension, and strategy. Mastery comes not just from memorizing formulas, but from developing a deeper understanding of the relationships and properties that govern geometric figures. With focused effort, you can enhance your problem-solving abilities and achieve greater confidence in tackling more complex challenges.
By using a structured approach, reviewing essential theorems, and practicing various types of problems, you can build a strong foundation for success. Here are some helpful tips to guide your learning process.
Review Fundamental Theorems and Formulas
Understanding and memorizing key theorems and formulas is crucial. These are the building blocks of many problems and will help you work through challenges more efficiently. Focus on the most commonly used principles, such as the properties of triangles, angle relationships, and area and perimeter formulas. Regularly revisiting these concepts will solidify your grasp and make it easier to apply them in various contexts.
Practice with a Variety of Problems

The more problems you solve, the more familiar you will become with different techniques and solutions. Challenge yourself with problems of varying difficulty to strengthen your problem-solving skills. Work through both basic and more advanced questions to ensure a well-rounded understanding of the material. Practice also helps identify patterns in the types of questions asked and prepares you to tackle similar problems on exams or assignments.
How to Approach Complex Problems
When faced with difficult problems, it’s easy to feel overwhelmed or unsure where to start. However, complex questions can often be broken down into smaller, more manageable parts. By adopting a methodical approach, you can gradually build your way toward a solution while avoiding common pitfalls. The key to solving intricate problems is to stay organized, remain patient, and use logical reasoning to guide your steps.
By following a structured process and utilizing specific strategies, you can improve your ability to tackle challenging questions with confidence. Here are some tips to approach complex problems effectively:
1. Understand the Problem Clearly
- Read through the problem multiple times to ensure a full understanding of what is being asked.
- Identify key information and any conditions that must be considered before starting the solution.
- Visualize the problem by drawing diagrams, if applicable, to better grasp the relationships between different elements.
2. Break the Problem into Smaller Steps
- Divide the problem into smaller, simpler sections that are easier to manage.
- Work on one part at a time, and don’t hesitate to approach it from different angles if necessary.
- Use known formulas and theorems to tackle each section, and gradually combine them to form the complete solution.
Understanding Coordinate Geometry Basics

In the study of spatial relationships, it’s essential to grasp the basics of how points and shapes are positioned on a plane. The key to this lies in understanding how to represent and manipulate coordinates in a two-dimensional space. Using an ordered pair of numbers, you can locate points on a grid, perform calculations involving distances, and even describe the properties of geometric shapes in a more precise and analytical manner.
Coordinate geometry allows you to connect abstract geometric concepts with a tangible numerical framework, providing a more systematic way to solve problems involving shapes, lines, and angles. Below is a summary of the fundamental concepts related to coordinates:
| Concept | Description |
|---|---|
| Coordinate Plane | A two-dimensional space formed by two perpendicular axes, the x-axis and y-axis, where points are located using ordered pairs (x, y). |
| Origin | The point of intersection of the x-axis and y-axis, denoted as (0, 0). |
| Distance Formula | A formula used to calculate the distance between two points on a plane: d = √((x2 – x1)² + (y2 – y1)²). |
| Midpoint Formula | A formula used to find the midpoint of a segment between two points: Midpoint = ((x1 + x2)/2, (y1 + y2)/2). |
How to Use the Distance Formula
When working with points on a plane, it’s often necessary to find the distance between them. The distance formula is a powerful tool that allows you to determine how far apart two points are, based on their coordinates. By applying this formula, you can solve a variety of problems involving spatial relationships, whether you’re analyzing the length of a line segment or calculating distances in real-world scenarios.
The formula is derived from the Pythagorean theorem, and it provides a straightforward method for calculating the distance between two points. Here’s a step-by-step guide to using the distance formula:
| Step | Explanation |
|---|---|
| Step 1 | Identify the coordinates of the two points. Let’s call them (x₁, y₁) and (x₂, y₂). |
| Step 2 | Subtract the x-coordinates: (x₂ – x₁), and subtract the y-coordinates: (y₂ – y₁). |
| Step 3 | Square both differences: (x₂ – x₁)² and (y₂ – y₁)². |
| Step 4 | Add the squared differences together: (x₂ – x₁)² + (y₂ – y₁)². |
| Step 5 | Take the square root of the sum to find the distance: d = √[(x₂ – x₁)² + (y₂ – y₁)²]. |
By following these steps, you can easily calculate the distance between any two points on a plane. This method is essential for solving problems in various mathematical fields and is a fundamental skill for students and professionals alike.
Exploring Similarity and Congruence
In the study of shapes and figures, two fundamental concepts that arise are similarity and congruence. While both deal with relationships between shapes, they have distinct characteristics. Similarity refers to figures that have the same shape but may differ in size, while congruence indicates that two figures are identical in both shape and size. Understanding these concepts is essential for solving various problems involving geometric transformations, measurements, and comparisons.
Understanding Similarity
Two figures are considered similar if they have the same shape but do not necessarily have the same size. Similar figures are related by a scale factor that allows one figure to be resized to match the other. Key features of similar figures include:
- The corresponding angles are equal.
- The corresponding sides are proportional, meaning the ratio of the sides is constant.
- They maintain the same shape, but their size may vary.
Understanding Congruence

Congruent figures, on the other hand, are exactly the same in both size and shape. They can be transformed through rotations, translations, or reflections to perfectly overlap. Key features of congruent figures include:
- Corresponding sides are equal in length.
- Corresponding angles are equal in measure.
- The figures can be transformed into one another without changing their size or shape.
Both similarity and congruence are crucial for understanding relationships between geometric shapes and for solving problems involving proportions, transformations, and symmetry. Recognizing these properties helps in identifying and working with geometric figures in various contexts, from basic measurements to advanced applications.
Real-World Applications of Geometry
The principles of spatial relationships, measurements, and shapes have far-reaching applications in various fields of everyday life. Understanding these concepts is not limited to abstract problems but extends to numerous practical situations. From architecture to technology, the ability to analyze and solve spatial challenges is crucial in making informed decisions and creating efficient designs. Here are some areas where knowledge of these concepts is commonly applied:
Architecture and Construction
In the construction of buildings, bridges, and other structures, precise measurements and the understanding of shapes are essential. These principles help architects and engineers create safe, stable, and aesthetically pleasing designs. Some key applications include:
- Designing floor plans and blueprints
- Calculating material quantities based on surface area
- Ensuring structural integrity through the study of angles and load distribution
Technology and Computer Graphics
In the world of technology, especially in computer graphics and animation, shapes and their properties are used to create realistic 3D models and simulations. Professionals in this field use concepts such as scale, proportion, and symmetry to create visually accurate and interactive designs. Examples include:
- Modeling virtual objects for video games and films
- Rendering computer-generated imagery (CGI) for animation
- Creating user interfaces and app designs with proportional layouts
Navigation and Cartography
When traveling or mapping out areas, geometric concepts play a key role in navigation and cartography. Understanding distances, angles, and coordinates is critical for determining routes, plotting maps, and ensuring accurate positioning. Key uses include:
- Creating and interpreting maps
- Using GPS for real-time positioning and route planning
- Calculating distances between locations for optimal travel paths
Art and Design
In the world of visual art, geometry serves as a foundation for creating balanced, proportional, and harmonious works. Whether designing logos, paintings, or sculptures, artists rely on spatial relationships to convey meaning and aesthetics. Some examples include:
- Using symmetry and proportion in design layouts
- Creating patterns and shapes in artwork
- Applying geometric principles in architecture and interior design
These applications show just a few ways that the study of shapes, sizes, and their relationships is integral to solving real-world problems. From practical uses in construction to creative endeavors in the arts, understanding these concepts is essential for success in numerous fields.
Practice Questions for Mastery
To strengthen your understanding of the material, it is important to apply the concepts through practical exercises. Below are several questions designed to challenge your knowledge and help reinforce the key principles. These questions cover a variety of topics, allowing you to test your problem-solving skills and ensure that you are well-prepared for more complex tasks. Try to solve each one carefully and check your progress as you go.
Basic Problems
Start with some foundational questions to ensure you understand the core concepts:
- What is the perimeter of a rectangle with length 8 units and width 5 units?
- Find the area of a triangle with a base of 6 units and a height of 4 units.
- Calculate the distance between the points (3, 2) and (7, 6) on a coordinate plane.
Intermediate Challenges

Once you feel confident with the basics, move on to slightly more challenging problems:
- In a right triangle, if the legs measure 5 units and 12 units, what is the length of the hypotenuse?
- Two similar triangles have corresponding sides in the ratio 3:4. If one triangle has a side length of 6 units, what is the corresponding side in the second triangle?
- Find the angle measures of a triangle given that two of its angles are 45° and 90°.
Advanced Questions
These problems will test your deeper understanding of more complex applications:
- Given a quadrilateral with angles measuring 70°, 120°, 85°, and 85°, determine if it is possible to classify this shape based on its angles.
- In a circle, the radius is 10 units. What is the area of the sector with a central angle of 60°?
- Using the properties of congruent triangles, prove that two triangles with angles measuring 30°, 60°, and 90° are congruent if the sides are equal in length.
These practice questions aim to challenge your understanding and offer a variety of difficulty levels. By testing your skills with both basic and advanced problems, you can enhance your problem-solving abilities and reinforce key concepts for future applications.