
Preparing for standardized assessments in mathematics can be a challenging yet rewarding experience. Understanding the structure of the questions and mastering the core concepts is essential for success. The process involves analyzing different types of problems, applying problem-solving techniques, and refining strategies for efficient completion. With the right approach, students can not only perform well but also deepen their understanding of the subject matter.
In this section, we will explore key elements of the test, break down common problem types, and provide a comprehensive guide to tackling complex mathematical challenges. By focusing on practice and understanding the solutions, students will be able to grasp the methods used to arrive at correct conclusions. The focus is not just on the final result but on the steps that lead to it, which are crucial for building a strong foundation in mathematics.
Whether you’re looking to improve your scores or simply understand the material more thoroughly, this guide will equip you with the tools necessary to approach each question with confidence.
2008 AP Calculus Exam Answers

Understanding how to solve advanced mathematical problems is critical for students aiming to perform well on a high-level assessment. This section provides a detailed look at how to approach the various sections of the test, offering step-by-step explanations of solutions and methods used to arrive at correct results. Whether it’s handling complex equations or interpreting graphs, mastering these techniques will enhance problem-solving abilities and test performance.
Key Problem Types and Their Solutions
- Problems requiring integration and differentiation techniques.
- Geometric questions involving slopes and areas.
- Questions based on real-world applications of mathematical concepts.
- Analysis of functions and their behaviors over different intervals.
Approach to Free-Response Questions
- Carefully read each question to understand what is being asked.
- Identify the most appropriate method or formula to solve the problem.
- Show all intermediate steps for maximum points.
- Ensure that your final answer is clearly stated and matches the required units or form.
By focusing on problem-solving strategies and understanding the methodology behind each type of question, students can improve their performance significantly. Practice with a variety of problem sets and familiarizing oneself with the common techniques will help achieve mastery of the material.
Overview of the 2008 Exam Format
The structure of a high-level mathematics assessment is carefully designed to test both knowledge and problem-solving abilities. The test is divided into different sections, each focused on various mathematical concepts. Understanding the organization of these sections is essential for effective preparation and strategic time management during the assessment.
- Multiple-Choice Section: This section assesses general knowledge and the ability to quickly apply mathematical concepts to solve problems.
- Free-Response Section: In this part, students must demonstrate their ability to explain their solutions in detail and solve complex, multi-step problems.
- Time Management: Each section is timed, requiring students to manage their time effectively to complete all questions.
The key to performing well in the test lies not only in mastering individual topics but also in developing strategies to tackle each section efficiently. The multiple-choice questions generally require quick calculations, while the free-response section demands a deeper understanding and clear communication of thought processes.
Key Topics Covered in the Test
The test is designed to assess a wide range of mathematical concepts that are essential for higher-level problem-solving. These topics are foundational to understanding advanced mathematics and are tested through various types of questions. Mastering these key areas will greatly enhance a student’s ability to succeed in the assessment.
- Limits and Continuity: Understanding how functions behave as they approach specific values and ensuring their smooth progression without abrupt changes.
- Derivatives: Calculating rates of change, determining slopes of tangents, and applying rules for differentiation.
- Integrals: Techniques for finding areas under curves and solving problems related to accumulation and total change.
- Applications of Derivatives and Integrals: Using derivatives for optimization and motion problems, and applying integrals in areas like volume and total distance.
- Series and Sequences: Understanding infinite sums, convergence, and working with series expansions.
These topics are integrated into both multiple-choice and free-response questions, and mastering them ensures a well-rounded approach to the test. Strong foundational knowledge in these areas will help students tackle both straightforward and complex problems with confidence.
Multiple-Choice Questions Explained

The multiple-choice section of the assessment is designed to evaluate a student’s ability to quickly apply mathematical concepts and select the correct solution from a set of options. These questions typically test fundamental principles and require students to recognize the best method for solving a problem in a time-efficient manner.
Each question is followed by several possible answers, but only one is correct. To succeed in this section, students must first carefully read the question and understand what is being asked. Often, there will be distractor answers designed to test common misconceptions or errors, so it’s important to analyze each option critically.
- Identifying Key Information: Focus on the given values and the mathematical relationships between them. This will help determine which method to use.
- Eliminating Incorrect Options: Narrow down the choices by eliminating answers that clearly do not match the problem’s requirements.
- Time Efficiency: Practice with time constraints to ensure you can answer each question quickly without sacrificing accuracy.
By honing these skills, students can improve their performance in the multiple-choice section, ensuring that they can solve problems efficiently and with confidence. Regular practice is key to becoming familiar with the types of questions and their solutions.
Free Response Section Breakdown
The free-response section of the test requires students to demonstrate their ability to solve complex problems while explaining their thought process clearly and concisely. Unlike multiple-choice questions, this section involves step-by-step problem-solving, where the process is just as important as the final answer. The ability to break down a problem and communicate each step effectively is crucial to scoring well in this part.
In this section, each problem typically involves multiple parts, with questions designed to assess deeper understanding and application of mathematical concepts. Students are expected to not only arrive at the correct solution but also show how they got there. Proper presentation of work is essential, as partial credit is awarded for logical steps even if the final answer is incorrect.
- Step-by-Step Solutions: Clearly show all the steps involved in solving the problem, even if they seem simple. This helps demonstrate your understanding.
- Explanations of Methods: When applicable, explain why you chose a particular method or approach for solving the problem.
- Attention to Detail: Pay attention to units, signs, and rounding. Mistakes in these areas can cost valuable points.
- Time Management: Make sure to allocate enough time for each problem. While detailed explanations are important, avoid spending too much time on one part of a problem.
Mastering this section requires both a solid understanding of the material and the ability to communicate that understanding effectively. Practicing problem sets and reviewing common techniques will help you perform better in the free-response section and improve your overall score.
Common Mistakes in 2008 Exam

Many students face similar challenges when tackling high-level mathematical assessments. These errors can range from misinterpreting questions to making small calculation mistakes that can significantly affect the final result. Understanding the most common pitfalls can help students avoid them and improve their performance on the test.
- Misreading Questions: A frequent mistake is not fully understanding the question before beginning the solution. It is essential to carefully read all instructions and identify what the problem is asking for.
- Skipping Steps: Omitting intermediate steps to save time can lead to incorrect answers. Always show your work to ensure clarity and to catch potential errors along the way.
- Incorrect Application of Formulas: Using the wrong formula or applying a concept incorrectly can lead to significant mistakes, especially in more complex problems.
- Neglecting Units or Signs: Missing units or neglecting negative signs in calculations can result in incorrect final answers, even if the approach was correct.
- Time Management Issues: Spending too much time on one question can affect the ability to complete others. Practice pacing to ensure all questions are addressed within the time limit.
By being aware of these common mistakes, students can approach the test with a better strategy and avoid costly errors. Regular practice and reviewing past assessments can also help minimize these pitfalls.
How to Approach Calculus Problems
Successfully solving mathematical problems requires more than just knowing the right formulas. It involves understanding the structure of the problem, identifying the appropriate methods, and applying them systematically. The key to approaching complex problems is breaking them down into manageable parts and staying organized throughout the process.
- Understand the Problem: Carefully read the question and ensure you fully understand what is being asked. Identify the key information and what the problem is trying to solve.
- Choose the Right Approach: Once you understand the problem, decide on the best method to solve it. Whether it’s using integration, differentiation, or another technique, having a clear strategy is crucial.
- Work Step by Step: Avoid skipping steps. Show your work clearly and logically, as this helps prevent errors and makes it easier to follow your solution.
- Check for Mistakes: After reaching a solution, take a moment to review your work. Look for any calculation errors, sign mistakes, or overlooked details like units or boundary conditions.
Approaching problems methodically helps to avoid common errors and ensures that you are following the correct procedures. Practice is essential, as familiarity with different types of problems improves both speed and accuracy.
Understanding Grading Criteria
To perform well in any rigorous assessment, it is essential to understand how your work will be evaluated. Grading criteria are designed to assess not only the correctness of your answers but also your ability to clearly demonstrate your reasoning and problem-solving process. Knowing these standards can help you focus on the areas that matter most and maximize your score.
The grading system generally considers several factors beyond just the final answer. In many cases, partial credit is awarded for logical steps, even if the final solution is incorrect. This emphasizes the importance of showing your work and clearly explaining your approach.
- Accuracy of Solutions: Correctness is critical. Ensure that your final answer is accurate, considering any units or signs.
- Clarity of Work: Present each step of your solution in a clear and organized manner. This helps graders follow your reasoning and award partial credit for correct processes.
- Justification of Methods: Explain why you chose specific methods to solve the problem, especially in more complex multi-step questions.
- Logical Consistency: Each step should follow logically from the previous one. Consistency in your approach strengthens your solution.
Familiarizing yourself with the grading criteria and focusing on these aspects will help ensure that your work meets the expectations and improves your chances of earning a higher score.
Practice Problems for Exam Preparation
One of the best ways to prepare for a challenging mathematical assessment is through consistent practice. By working through various problems, students can familiarize themselves with the types of questions they will encounter and improve both their problem-solving skills and time management. Practice problems help reinforce concepts, build confidence, and reveal areas that need further review.
To make the most of your practice, focus on a variety of problem types and difficulty levels. This will ensure you are well-rounded and ready for any challenge that arises during the assessment.
Key Topics to Focus On
- Limits and Continuity: Work on problems that require you to evaluate the behavior of functions at specific points or as they approach infinity.
- Derivatives and Integrals: Practice finding derivatives and integrals of different types of functions, paying close attention to special rules like the chain rule and integration by parts.
- Applications of Differentiation: Solve problems that involve related rates, optimization, and motion, all of which test your ability to apply theoretical knowledge to practical situations.
- Area and Volume Problems: Work on problems that require you to calculate areas under curves or volumes of solids, as these are common in many assessments.
Effective Practice Strategies
- Timed Practice Sessions: Simulate test conditions by setting a timer while solving practice problems. This will help you develop better time management skills and ensure you can complete the entire assessment within the allotted time.
- Review Mistakes: After completing practice problems, review your mistakes carefully. Understanding why you made an error is crucial for improving your approach to similar problems in the future.
- Use Multiple Resources: Don’t limit yourself to just one set of practice problems. Use textbooks, online resources, and past assessments to ensure you are exposed to a wide range of question types and formats.
By incorporating regular practice into your study routine, you will gain a deeper understanding of the material and be better prepared to tackle any challenge that comes your way.
Score Interpretation and What It Means

Interpreting your performance on a rigorous assessment is crucial for understanding your strengths and areas that need improvement. The score you receive provides insight into your grasp of the material, but it also reflects how well you can apply that knowledge under timed conditions. A good understanding of how scores are calculated and what each range signifies can guide you in making informed decisions about your academic progress and future goals.
Scores are typically divided into categories, each representing a different level of proficiency. These categories help you assess not only how much you know but also how well you can apply your knowledge in problem-solving situations.
Understanding Score Ranges
- Top Scores: Achieving a high score generally indicates a solid understanding of the concepts and the ability to solve complex problems effectively. A top score can open doors for college credit or advanced placement in future courses.
- Average Scores: An average score suggests that while you may have a decent understanding of the material, there are areas that need improvement. This score is often indicative of partial mastery but may require additional study or practice for further improvement.
- Low Scores: A low score typically points to a lack of sufficient understanding in key areas. It’s essential to identify which topics were the most challenging and address those gaps before retaking the assessment or moving on to more advanced material.
What Your Score Means for Your Future
- College Credit: Many institutions offer credit for high scores, allowing you to bypass introductory courses or earn advanced placement in related subjects. High performance may also strengthen your college application.
- Areas for Improvement: If your score is lower than expected, use it as a guide to identify specific concepts that need further review. Focusing on weak points can help raise your score in future attempts.
- Self-Reflection: Your score can be a useful tool for self-reflection. If you performed better than expected, it might be time to consider taking on more challenging material. If your performance was below expectations, take the time to reassess your study habits and seek additional resources or support.
Ultimately, understanding the significance of your score goes beyond just the number itself. It’s about gaining clarity on where you excel, where you need improvement, and how to use that information to shape your future academic pursuits.
Strategies for Time Management
Effectively managing your time during a challenging test is essential for ensuring that you can complete all sections within the allotted time. Good time management allows you to pace yourself, reduce stress, and maximize your performance by focusing on high-priority areas. By following certain strategies, you can improve your ability to stay on track and handle even the most difficult questions with confidence.
Developing a time management plan before the test begins can help you stay organized and avoid rushing through questions at the last minute. Here are some practical strategies that can enhance your ability to manage your time effectively:
- Familiarize Yourself with the Test Format: Knowing the structure of the test allows you to allocate time to each section appropriately. This ensures that you can spend more time on complex problems while ensuring that simpler ones don’t eat up too much of your time.
- Set a Time Limit for Each Question: Assign a specific amount of time to each question or problem type. If you’re stuck on a difficult question, move on to the next one and come back later. This ensures that you don’t waste too much time on one problem.
- Prioritize Questions: Start with questions that you feel most confident about. This will build momentum and boost your confidence early on. Save the more difficult or time-consuming questions for later when you’ve already made progress.
- Use a Timer: Bring a watch or use the test’s built-in timer to keep track of time. This allows you to check your progress regularly and adjust your pace if necessary.
- Practice Under Timed Conditions: To simulate the pressure of a real test, practice solving problems under timed conditions. This will help you become more comfortable with the time constraints and improve your ability to manage them on the day of the test.
By using these time management strategies, you can ensure that you approach your test with a calm, focused mindset. Efficient time management not only improves your performance but also reduces anxiety, allowing you to tackle each problem with a clear and strategic approach.
Recommended Resources for Review
Preparing for a rigorous assessment requires access to high-quality resources that help reinforce your understanding and improve problem-solving skills. Utilizing a variety of materials can give you the advantage of seeing different approaches and gain deeper insight into challenging topics. Whether you prefer textbooks, online platforms, or practice tests, using the right resources will ensure a comprehensive review.
Here are some recommended materials that can enhance your study routine and guide you toward success:
- Textbooks and Study Guides: Comprehensive textbooks offer detailed explanations of key concepts, step-by-step examples, and practice exercises. Study guides specifically designed for the assessment can provide condensed material with focus on the most commonly tested topics.
- Online Learning Platforms: Websites like Khan Academy, Coursera, and edX provide free and paid courses, videos, and exercises tailored to the subject matter. These platforms often include interactive elements that can boost retention and understanding.
- Practice Tests: Taking practice tests under timed conditions is one of the best ways to prepare. These simulate the actual testing environment and give you a clear understanding of where you may need improvement. Use past tests or test preparation books that offer full-length exams.
- Flashcards: Flashcards can be a helpful tool for memorizing formulas, important concepts, and definitions. Many online platforms like Quizlet provide pre-made sets, or you can create your own to focus on weak areas.
- Tutoring and Study Groups: Working with a tutor or in a study group allows you to discuss complex concepts and gain different perspectives. Collaboration can help clarify any confusion and reinforce your understanding of challenging topics.
By incorporating these resources into your study routine, you can build a strong foundation and approach your preparation with confidence. The right tools and strategies will make the review process more efficient and effective, leading to better outcomes on the day of the assessment.
How to Improve Calculus Skills
Mastering advanced mathematical concepts requires consistent practice, a solid understanding of foundational principles, and the ability to apply theory to solve problems. Whether you’re just starting or aiming to refine your proficiency, focusing on specific strategies can significantly enhance your problem-solving abilities and overall understanding. By dedicating time and employing targeted methods, you can improve both your speed and accuracy in tackling complex mathematical challenges.
Here are some effective ways to sharpen your skills and build confidence in advanced mathematics:
- Strengthen Your Fundamentals: Ensure that your grasp of basic algebra, trigonometry, and geometry is solid. These subjects form the foundation for more advanced topics and will make learning higher-level concepts easier and more intuitive.
- Practice Regularly: The key to improvement is practice. Work on a variety of problems daily, focusing on different types of questions. This will help you familiarize yourself with various problem-solving techniques and patterns.
- Work Through Examples: Studying solved examples helps you understand the steps involved in solving a problem. Try to follow the logic of each example and attempt similar problems without looking at the solutions.
- Focus on Problem-Solving Strategies: Learn different approaches to solving problems, such as breaking down complex questions into smaller, manageable steps or using estimation techniques. This will help you tackle unfamiliar problems with confidence.
- Review Mistakes and Learn from Them: When you make errors, take the time to analyze them. Understanding why you made a mistake and how to correct it will prevent you from repeating the same errors and deepen your understanding.
- Utilize Online Resources: Take advantage of educational platforms, instructional videos, and interactive tools. Online resources provide different perspectives and methods, making it easier to understand difficult topics.
By following these strategies, you can gradually build your expertise and increase your ability to solve problems with ease. Consistent practice and active learning are the keys to achieving proficiency and excelling in advanced mathematical subjects.
Real-Life Applications of Calculus
Mathematical concepts extend far beyond the classroom and have a significant impact on our everyday lives. The principles used in solving complex equations are applied to various fields, offering solutions to real-world problems. By understanding the theory behind these concepts, professionals in fields such as engineering, economics, physics, and computer science can devise innovative solutions to challenging problems. These applications provide insight into the power of advanced mathematics and its usefulness in shaping modern technology and society.
Applications in Engineering
Engineers frequently use advanced mathematical techniques to design systems, optimize structures, and predict outcomes. Calculus plays a crucial role in determining things like material stress, fluid dynamics, and electrical circuits. For example, calculus helps engineers calculate the optimal dimensions for components to ensure efficiency, safety, and sustainability.
Applications in Economics
Economists rely on mathematical models to predict market trends, set pricing strategies, and optimize resource allocation. Calculus helps in understanding the behavior of economies by analyzing rates of change in production and consumption. It allows for the creation of models that can predict future economic outcomes based on current data.
Applications in Medicine and Biology
In fields like medicine and biology, calculus is used to model the growth rates of diseases, the spread of infections, and the change in the concentration of drugs in the bloodstream. Medical researchers use mathematical models to understand the effectiveness of different treatments and the potential outcomes of various medical interventions.
Other Key Fields
Other industries, such as robotics, astronomy, and environmental science, also rely heavily on advanced mathematics. From predicting the trajectory of spacecraft to analyzing environmental data, the ability to model and solve real-world problems is essential to solving many modern challenges.
Table of Common Applications
| Field | Application | Real-World Impact |
|---|---|---|
| Engineering | Optimizing structures and systems | Increased efficiency, safety, and sustainability |
| Economics | Market prediction and resource allocation | Better decision-making and economic forecasting |
| Medicine | Modeling disease spread and treatment effects | Improved healthcare outcomes and treatment planning |
| Physics | Understanding forces, energy, and motion | Inventions like renewable energy solutions and transportation systems |
The widespread use of these mathematical principles highlights their importance in both scientific advancements and practical applications. Whether in predicting the future or understanding the past, the tools provided by advanced mathematics are indispensable in modern life.
Insights from Past Exam Takers
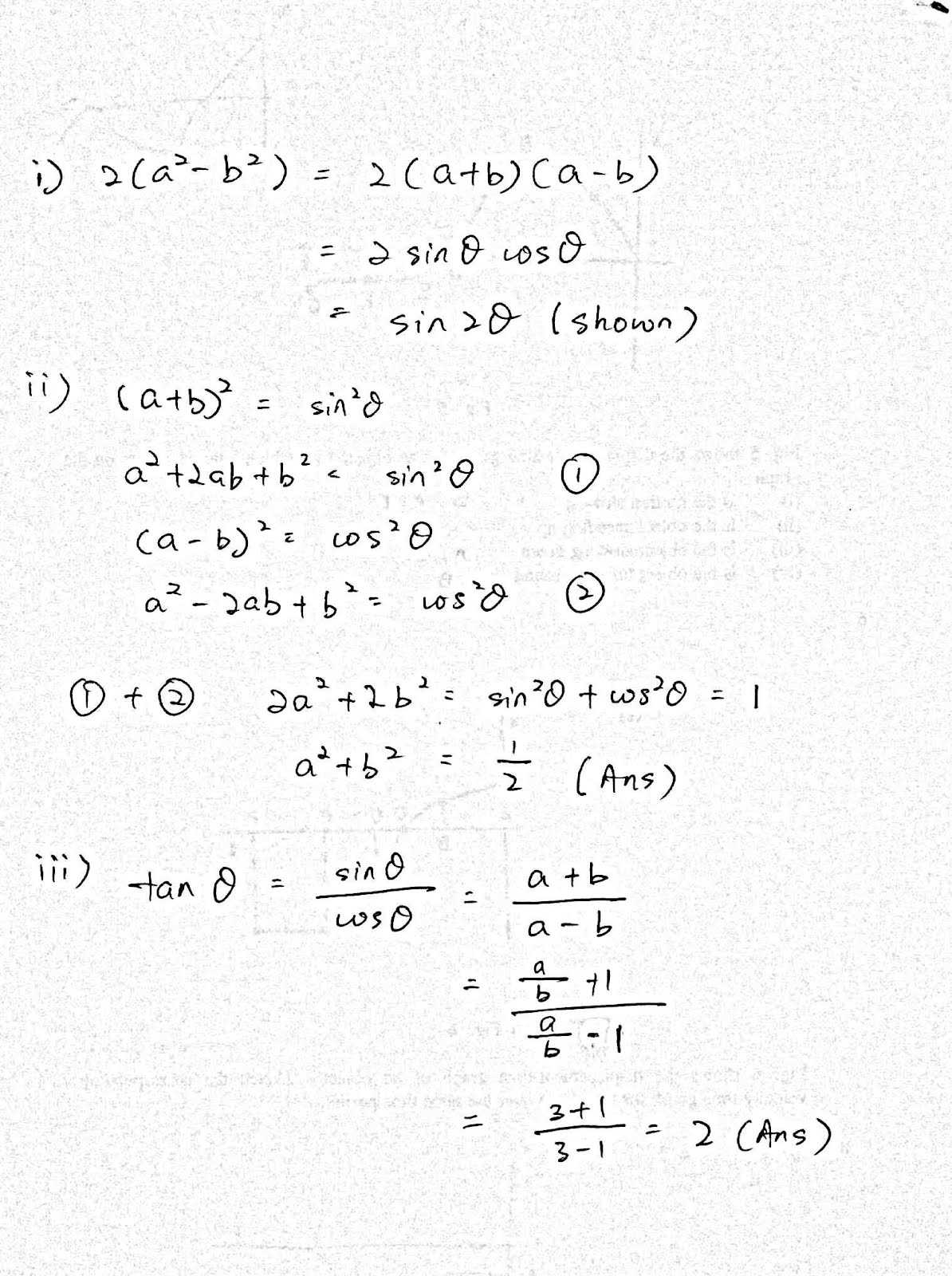
Many students who have previously gone through this rigorous assessment have shared valuable tips and strategies that helped them succeed. Learning from their experiences can provide new test-takers with a clearer understanding of the challenges and effective methods to approach the various sections of the test. Past candidates often recommend techniques for managing time, improving accuracy, and boosting confidence during the process. These insights not only reflect the best study practices but also highlight common pitfalls that many encounter.
Students emphasize the importance of focused preparation, understanding the types of questions, and practicing with real past problems to build familiarity. Furthermore, many past participants suggest staying calm and organized during the test, as anxiety can hinder performance. By reviewing feedback from those who have already navigated this journey, future test-takers can be better equipped for success.
Key Takeaways from Former Test-Takers
| Tip | Reason | Impact |
|---|---|---|
| Practice Under Timed Conditions | Simulates real test environment | Improves time management and reduces test anxiety |
| Focus on Weak Areas | Target areas with the most potential for improvement | Increases overall score by strengthening weak spots |
| Review Previous Mistakes | Helps avoid repeating the same errors | Boosts accuracy and confidence during the test |
| Understand the Scoring System | Clarifies how points are awarded | Helps prioritize sections to maximize points |
By incorporating these strategies, future candidates can build a more effective study routine, avoid common mistakes, and improve their chances of achieving a high score. The collective wisdom from past test-takers proves that preparation is the key to mastering the challenges presented in the assessment.
Tips for Success in AP Calculus
Achieving success in this advanced-level assessment requires not only understanding the key concepts but also developing effective strategies for preparation and test-taking. Success is often determined by consistent practice, mastering the fundamentals, and applying critical thinking to solve complex problems. To excel, it is essential to combine theoretical knowledge with practical problem-solving skills, ensuring that you’re well-prepared for every challenge the test may present.
One important aspect is focusing on both conceptual understanding and procedural fluency. Simply memorizing formulas will not be enough to secure a high score. Instead, practice regularly and focus on understanding the principles behind each concept, which will help you tackle unfamiliar questions with confidence. Additionally, practicing with real test problems under timed conditions can help you become familiar with the exam format and improve time management skills.
Key Tips for Mastery
- Practice Regularly: Consistent practice is crucial for reinforcing learned concepts and improving problem-solving speed.
- Master Core Concepts: Understanding the theory behind each topic is essential for applying it to different problem scenarios.
- Work on Time Management: Practice solving problems under time constraints to simulate real test conditions.
- Review Mistakes: Learn from errors by reviewing solutions and understanding why mistakes were made.
- Use Reliable Resources: Leverage textbooks, online tutorials, and practice tests to deepen understanding and reinforce learning.
Incorporating these strategies into your study routine will help you build the necessary skills and confidence to succeed. By maintaining a disciplined approach to preparation, future test-takers can greatly improve their chances of mastering the material and performing well under pressure.