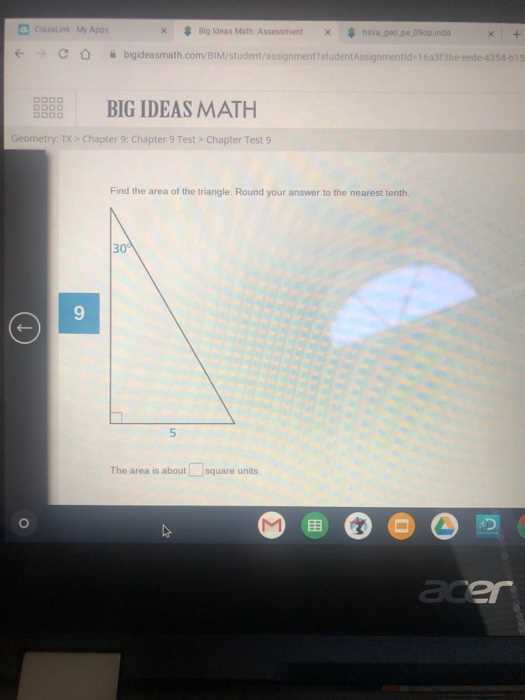
Understanding the intricacies of spatial relationships and geometric structures is crucial for solving complex problems in this area. In this section, learners are introduced to a variety of techniques that help in tackling various mathematical challenges, with a focus on precise reasoning and visualization. The methods explored here are designed to strengthen both foundational knowledge and critical thinking skills.
Focusing on key principles and their applications allows for a deeper comprehension of the subject matter. This section goes beyond basic formulas and delves into more advanced topics, ensuring a well-rounded grasp of how shapes interact, transform, and relate to one another in a variety of contexts. By mastering these concepts, students can build a solid foundation for tackling even more complex tasks in future studies.
Throughout this guide, we will examine various approaches to problem-solving, offering clear explanations and practical exercises. By engaging with the material and refining problem-solving strategies, learners will be better equipped to approach similar challenges in exams and real-world scenarios.
Big Ideas Math Geometry Chapter 5 Overview
This section introduces important concepts and methods that help solve complex problems related to shapes, sizes, and their relationships. It explores both theoretical and practical aspects, offering a deeper understanding of spatial reasoning. The goal is to equip learners with the skills necessary to analyze geometric situations and apply logical techniques to find solutions.
Core Concepts Explored
Students will engage with key principles such as transformations, symmetry, and the properties of different geometric figures. These concepts form the backbone of more advanced topics, providing the foundation for tackling real-world challenges. By the end of this section, learners will be able to recognize patterns, make connections, and apply these principles in various contexts.
Problem-Solving Techniques
This section also emphasizes the importance of clear problem-solving strategies. Through a series of examples and exercises, students will learn how to break down complex tasks into manageable steps. The focus is on developing critical thinking skills and becoming proficient at using geometric reasoning to approach various scenarios effectively.
Key Concepts in Chapter 5
This section focuses on the fundamental principles and techniques that form the core of this unit. It explores various concepts related to spatial relationships and the manipulation of different figures, providing the necessary tools for effective problem-solving. Understanding these key ideas is crucial for building a strong foundation in the subject.
Important Principles
- Transformations: Understanding how shapes move, rotate, and reflect in space.
- Symmetry: Recognizing symmetrical properties in different geometric figures.
- Congruence and Similarity: Identifying when shapes are identical or proportionally equivalent.
- Angles and their relationships: Exploring different types of angles and how they interact in various figures.
Applications of Concepts
- Using transformations to solve real-world problems involving design and symmetry.
- Applying congruence to determine shape equivalence in practical scenarios.
- Analyzing angles in architectural plans and structural designs.
- Recognizing patterns in nature and other scientific contexts using geometric principles.
Step-by-Step Solutions for Exercises
This section provides detailed instructions for solving various problems, guiding you through each step to ensure a clear understanding of the process. By breaking down complex tasks into manageable actions, students can better grasp how to approach similar exercises in the future. Each solution is designed to highlight key principles and strategies used to reach the correct answer.
Following a structured approach not only helps in solving individual problems but also builds the skills necessary for tackling more advanced challenges. As you work through the exercises, focus on the logical connections between each step and how they lead to the final solution. With practice, these techniques will become second nature, enhancing your overall proficiency in the subject.
Understanding Geometric Properties and Theorems
This section delves into the fundamental characteristics of shapes and the mathematical rules that govern their behavior. By examining these properties and theorems, students can develop a deeper understanding of how different figures interact with one another in space. A strong grasp of these concepts is essential for solving a wide range of problems and for applying geometric reasoning to real-world situations.
Geometric properties, such as symmetry, congruence, and proportionality, define how shapes are structured and how they can be transformed. Theorems, on the other hand, provide logical frameworks for proving relationships between these properties. By studying and applying these principles, students can not only solve problems but also justify their solutions with solid mathematical reasoning.
Important Formulas to Remember
Mastering the key equations and expressions is essential for solving a wide variety of problems in this subject. These formulas are the building blocks of problem-solving and provide the necessary tools to understand complex relationships between shapes and figures. Having a solid grasp of these formulas allows for quick application and efficient calculation when faced with different challenges.
| Formula | Application |
|---|---|
| Area of a Triangle: A = ½ × base × height | Used to find the area of any triangle when the base and height are known. |
| Pythagorean Theorem: a² + b² = c² | Calculates the length of a side in a right triangle when the other two sides are known. |
| Area of a Circle: A = π × r² | Used to find the area of a circle when the radius is known. |
| Circumference of a Circle: C = 2π × r | Calculates the distance around a circle when the radius is known. |
| Volume of a Rectangular Prism: V = length × width × height | Used to calculate the volume of a box-shaped figure when the dimensions are known. |
Common Mistakes in Geometry Problems
When solving spatial problems, it’s easy to make certain errors that can lead to incorrect results. These mistakes often arise from misunderstandings of key concepts or from rushing through calculations without careful attention. Identifying and avoiding these common pitfalls can significantly improve accuracy and efficiency when tackling geometry tasks.
Misunderstanding Relationships Between Shapes
A frequent mistake is assuming that certain figures are congruent or similar when they are not. It’s essential to carefully analyze the properties of each shape before applying specific theorems or formulas. For example, assuming two triangles are identical without checking side lengths and angles can lead to incorrect conclusions.
Incorrect Use of Formulas
Another common error is misapplying formulas, particularly when it comes to area and volume. For instance, confusing the area of a rectangle with the perimeter or mixing up the formula for the area of a triangle can cause significant mistakes. Always double-check that the correct formula is being used for the specific shape you’re working with.
Attention to detail is crucial in geometry. Small oversights, such as forgetting to square a value or misinterpreting angle relationships, can lead to larger errors down the line. Slow down and carefully evaluate each step to avoid these common mistakes and achieve more accurate results.
Strategies for Solving Geometry Questions

Effective problem-solving in spatial reasoning requires a structured approach and a clear understanding of the tools available. By using strategies that break down complex tasks into manageable steps, you can improve both accuracy and efficiency. These methods not only help in solving individual problems but also strengthen overall mathematical thinking.
Visualization and Diagram Drawing
One of the most powerful strategies is to draw a clear diagram of the given problem. Visualizing the situation helps identify key features, such as angles, sides, and symmetries, which are essential for applying the correct formulas. If a diagram is not provided, try sketching one based on the information given in the question. This can often simplify the process and reveal relationships between elements that might not be obvious at first.
Using Logical Step-by-Step Reasoning
Breaking down a problem into smaller, logical steps is another crucial approach. Start by identifying what is given and what needs to be found, and then apply the appropriate principles one step at a time. This method reduces the chances of missing important details and helps you avoid rushing through the solution process.
By practicing these strategies consistently, you’ll build confidence in solving a wide range of problems and be better prepared to handle more complex scenarios in the future.
Tips for Improving Problem-Solving Skills
Enhancing problem-solving abilities involves developing a deeper understanding of the tools and techniques available to tackle challenges effectively. With consistent practice and the right strategies, anyone can improve their ability to approach problems logically and systematically. This section provides actionable tips that can boost your problem-solving skills and lead to more efficient solutions.
| Tip | Benefit |
|---|---|
| Practice Regularly | Frequent practice strengthens problem-solving abilities and builds confidence in tackling different types of problems. |
| Work Backwards | Starting from the desired outcome and reversing the steps can offer new insights into solving the problem. |
| Understand the Problem | Carefully reading and understanding the problem ensures that you are applying the right concepts and strategies from the beginning. |
| Break Down Complex Problems | Dividing larger problems into smaller, more manageable parts makes it easier to focus on each individual step. |
| Stay Organized | Using clear, logical steps and keeping track of your work helps prevent mistakes and improves accuracy. |
By applying these tips consistently, you will develop stronger problem-solving skills, enabling you to handle a variety of challenges with greater ease and precision.
Visualization Techniques for Geometric Shapes
Visualization plays a crucial role in understanding spatial relationships and solving problems involving shapes. By forming a clear mental image of figures and their properties, you can approach problems more effectively and identify key patterns or connections that may not be immediately obvious. Using different visualization techniques helps clarify complex concepts and makes solving related problems easier.
One of the most useful techniques is creating detailed diagrams. Drawing shapes and labeling key elements, such as angles, sides, and vertices, allows you to visualize relationships and apply the correct mathematical principles. Additionally, rotating or flipping shapes in your mind can reveal hidden symmetries or relationships between elements that are vital for solving the problem.
Another effective method is breaking down complex figures into simpler components. For example, viewing a polygon as a combination of triangles can make it easier to calculate area or solve for unknown angles. By practicing these techniques, you can strengthen your ability to think spatially and improve problem-solving skills in various contexts.
How to Use Geometry Software for Practice
Utilizing digital tools can significantly enhance your ability to grasp geometric concepts and improve your problem-solving skills. Geometry software provides interactive features that allow you to manipulate shapes, experiment with different configurations, and visualize complex relationships in a dynamic way. With the right approach, these tools can serve as a powerful supplement to traditional learning methods.
Exploring Interactive Features
One of the main advantages of using geometry software is the ability to experiment with shapes and observe real-time changes. For example, you can easily modify the dimensions of a triangle, adjust angles, or rotate figures to explore their properties. This hands-on approach helps solidify theoretical concepts and provides a deeper understanding of spatial relationships. Take advantage of the software’s tools to create custom shapes and see how different changes affect the overall structure.
Using Software for Problem-Solving Practice
Another effective way to use geometry software is to practice solving problems. Many programs offer pre-loaded exercises and challenges that range in difficulty. These exercises help reinforce your knowledge by applying the concepts you’ve learned in a variety of contexts. As you work through the problems, use the software’s features to check your solutions, visualize steps, and experiment with different methods until you arrive at the correct answer.
Stay engaged by regularly using these tools in your practice routine. The more you explore and experiment, the more confident you’ll become in applying geometric principles to real-world problems. Incorporating software into your study habits can complement your textbook learning and provide a more immersive experience.
Real-World Applications of Geometry Concepts
The principles of spatial reasoning extend far beyond the classroom, influencing a wide range of industries and real-world scenarios. From architecture to computer graphics, the ability to understand and apply geometric concepts is essential for solving practical problems. These concepts form the foundation of numerous professions and everyday tasks, demonstrating their value in both creative and technical fields.
Design and Architecture
In the field of design, understanding the properties of shapes, angles, and symmetry is crucial. Architects rely heavily on spatial reasoning to create functional and aesthetically pleasing buildings. They use geometric principles to calculate dimensions, plan layouts, and ensure structural integrity. For example, when designing a building, architects must account for the angles of walls, the symmetry of windows, and the proportions of different elements to create harmony within the structure.
Technology and Computer Graphics
In technology, particularly in computer graphics, geometry plays a central role in the creation of visual content. Game developers, animators, and software engineers use geometric algorithms to model objects, animate movements, and render realistic images. 3D modeling, for instance, relies on the understanding of vertices, edges, and faces to create three-dimensional objects on screen. These principles are applied in video games, simulations, and virtual reality environments, where geometry helps create immersive experiences.
Understanding geometric principles is essential for anyone working in fields that involve design, construction, or technology. By recognizing how these concepts shape the world around us, you can see how they influence both everyday tasks and cutting-edge innovations. From the buildings we live in to the digital worlds we explore, geometric concepts are constantly at work.
How to Approach Chapter 5 Word Problems
Word problems often present a challenge as they require you to translate real-world scenarios into mathematical expressions. To solve these problems effectively, it is crucial to first carefully read the problem and identify the key information. By understanding the context and breaking the problem into smaller, manageable parts, you can apply relevant strategies to reach the solution. The key is to approach each problem systematically and methodically, ensuring that every detail is accounted for before attempting to solve it.
Step 1: Identify the given information – Start by pinpointing the values and conditions provided in the problem. These can be numbers, relationships, or constraints that will help you form equations. Once identified, make sure you understand how these elements are related to each other and what the problem is asking you to find.
Step 2: Translate the words into equations – Many word problems involve geometric relationships that can be expressed through equations. Look for keywords that indicate specific operations, such as “sum,” “difference,” or “product,” and translate them into mathematical symbols. For example, if the problem refers to the perimeter of a rectangle, you can use the formula for perimeter to form an equation.
Step 3: Solve and check your work – After setting up your equations, perform the necessary calculations. Be sure to double-check your work for accuracy. If the solution doesn’t make sense, re-examine the problem and ensure you haven’t missed any important details. Visualizing the problem with diagrams can often help clarify the solution and avoid errors.
By following these steps and practicing regularly, you can build confidence in solving word problems and improve your problem-solving skills. Remember, each problem presents a new opportunity to apply different strategies and deepen your understanding.
Understanding Diagrams in Geometry Problems
Diagrams are essential tools that help visualize the relationships between different elements in a problem. In many cases, interpreting these diagrams correctly can significantly simplify the process of finding a solution. Understanding how to read and analyze geometric figures is a crucial skill in solving problems effectively. By paying close attention to the details of a diagram, you can identify key information and apply the right formulas or reasoning to find the correct answer.
How to Analyze a Diagram
When presented with a diagram, consider the following steps to better understand it:
- Label the key elements: Identify points, lines, angles, and any other relevant figures. Labeling them can help you track the information as you solve the problem.
- Look for given information: Often, the problem will provide certain measurements directly in the diagram, such as side lengths or angles. Highlight these values to ensure you don’t overlook them.
- Identify the relationships: Pay attention to how the different parts of the diagram are related to one another. Are the angles complementary? Are there parallel lines? Understanding these relationships can guide your approach to solving the problem.
- Consider symmetry and proportions: In many problems, the diagram might display symmetrical shapes or proportional relationships that can simplify the calculations.
Common Mistakes to Avoid
While diagrams are helpful, it’s easy to make mistakes when interpreting them. Here are a few common errors to watch out for:
- Misinterpreting angles: Always ensure you understand the type of angle you’re working with (acute, obtuse, right, etc.) before applying formulas.
- Overlooking hidden information: Sometimes, diagrams include information that isn’t explicitly labeled but can be inferred. For example, some angles may be equal due to symmetry or parallel lines.
- Not scaling correctly: In some cases, diagrams might not be drawn to scale. Ensure you rely on the given measurements rather than assuming the diagram is accurate in size and proportion.
By practicing these strategies and carefully analyzing diagrams, you’ll develop a stronger understanding of the problem and improve your ability to solve complex geometric questions. Visualizing the problem can often provide insights that are not immediately obvious from the written text alone.
Practice Problems for Mastery

To truly master the concepts presented in this section, regular practice is essential. Solving a variety of problems helps reinforce key concepts and improves problem-solving skills. Through consistent practice, you can become more comfortable with applying the principles you’ve learned and better understand how to tackle complex questions. Below are some practice problems designed to enhance your understanding and sharpen your abilities.
Practice Problems

Here are a few problems that cover different aspects of the topic. Work through each one carefully and apply the strategies you’ve learned.
- Problem 1: Given a triangle with two sides measuring 8 cm and 15 cm, and an included angle of 45°, find the length of the third side using the Law of Cosines.
- Problem 2: A rectangle has a length of 10 m and a width of 4 m. Find the diagonal length of the rectangle using the Pythagorean Theorem.
- Problem 3: In a circle with a radius of 7 cm, calculate the circumference and area of the circle. Use the formulas C = 2πr and A = πr².
- Problem 4: Solve for the unknown angle in a quadrilateral where three angles are 85°, 95°, and 100°.
Steps to Solve Practice Problems
For each problem, follow these steps to ensure you approach it correctly:
- Read the problem carefully: Identify the known values and the unknowns. Write them down to keep track of the given information.
- Choose the correct formula or method: Depending on the problem, select the appropriate mathematical approach (e.g., Pythagorean theorem, trigonometry, area formulas, etc.).
- Perform the calculations: Carefully work through the math step by step. Show your work to ensure accuracy and avoid mistakes.
- Check your solution: After solving, double-check your work. Verify if the solution makes sense in the context of the problem.
By regularly practicing problems like these, you’ll gain confidence in your ability to apply the concepts you’ve learned and develop the skills necessary for tackling more challenging problems. Keep practicing, and you’ll see continuous improvement in your problem-solving capabilities.
Reviewing Key Theorems and Proofs
Understanding the fundamental theorems and their corresponding proofs is essential for building a strong foundation in solving complex problems. Theorems provide the logical framework for understanding relationships between different elements, while proofs verify the validity of these relationships. A thorough review of the most important theorems and their proofs will help you apply these concepts confidently to solve various problems.
Important Theorems to Remember
Here are several key theorems that are frequently used in this area of study. Make sure to familiarize yourself with each one and understand the logical reasoning behind it:
- The Pythagorean Theorem: In a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the other two sides. a² + b² = c²
- The Triangle Sum Theorem: The sum of the interior angles of any triangle is always 180°.
- The Angle Bisector Theorem: An angle bisector divides the opposite side of a triangle into two segments that are proportional to the adjacent sides of the triangle.
- The Converse of the Pythagorean Theorem: If the square of one side of a triangle is equal to the sum of the squares of the other two sides, the triangle is a right triangle.
Understanding Proofs
Theorems become useful only when they are backed up by solid reasoning through proofs. A proof demonstrates why a certain statement is true based on known principles. Here is an example of how a common proof is structured:
- State the theorem: For example, “The sum of the angles in a triangle equals 180°.”
- Set up the conditions: Consider a triangle with three interior angles.
- Provide logical steps: Use known geometric principles, such as parallel lines and angle relationships, to demonstrate how the sum of the angles is derived.
- Conclude: Show that the sum of the angles indeed equals 180°.
By reviewing and practicing these key theorems and their proofs, you will be able to approach geometric problems with a deeper understanding and greater confidence.
How to Prepare for Geometry Tests
Proper preparation is essential for performing well on assessments in this subject. Being familiar with core concepts, honing problem-solving skills, and practicing time management can significantly improve your test results. Effective preparation strategies will help you approach each problem with confidence and clarity, ensuring that you are ready for any challenge that comes your way.
Review Key Concepts and Theorems
Before the test, it is crucial to review all important concepts, including theorems, formulas, and definitions. Focus on the ones that frequently appear in practice problems and assessments. Make sure you understand how to apply each theorem and formula in various contexts. You can use the following methods:
- Make flashcards: Create flashcards for essential theorems and formulas to test your memory.
- Summarize key points: Write concise summaries of major concepts for easy reference.
- Review previous tests: Look at past assessments to understand the types of questions that are commonly asked.
Practice Problem-Solving Techniques
Consistent practice is the best way to build your problem-solving skills. Work through a variety of problems to ensure you are comfortable with different types of questions. Start with simpler problems to reinforce your understanding, then gradually move on to more challenging exercises. Additionally, time yourself while solving problems to improve your speed under pressure. Key strategies include:
- Work on sample problems: Solve a range of problems from your textbook, online resources, or study guides.
- Understand the steps: Focus on understanding the process of solving each problem rather than memorizing solutions.
- Seek help when needed: If you’re struggling with a specific concept, ask for clarification from a teacher or tutor.
By reviewing the material thoroughly and practicing regularly, you’ll improve your understanding and boost your performance on the test.
Final Tips for Success in Geometry

Achieving success in this subject requires a combination of consistent effort, strategic studying, and a strong grasp of key principles. By focusing on understanding the fundamental concepts, practicing regularly, and developing problem-solving techniques, you can overcome challenges and perform well in assessments. Here are some final strategies to help you reach your full potential.
Stay Organized and Manage Your Time

Effective time management is essential to mastering this subject. Organize your study materials and set aside specific times for practice. Break down complex topics into smaller, more manageable chunks, and allocate time each day to review and reinforce your understanding. By staying organized, you can prevent last-minute cramming and approach your studies with a clear plan.
Work on Understanding, Not Just Memorization
While memorizing formulas and theorems is important, true success comes from understanding how and when to apply them. Focus on grasping the underlying principles behind each concept. Try to see the connections between different topics and how they interrelate. This deeper understanding will allow you to approach problems from various angles and develop more flexible problem-solving skills.
Use Multiple Resources
Don’t rely on just one source of information. Expand your understanding by using a variety of materials such as textbooks, online tutorials, practice tests, and study groups. Each resource offers a different perspective, which can help you gain a more comprehensive understanding of the subject.
Stay Positive and Confident

A positive attitude and self-confidence are key factors in overcoming any challenges you may face. Believe in your ability to learn and improve. If you make mistakes, view them as learning opportunities rather than setbacks. With consistent effort and a proactive mindset, success is within reach.
By incorporating these strategies into your study routine, you will be better prepared to tackle any challenges that arise and excel in this subject. Keep practicing, stay organized, and trust in your ability to succeed.