
In this section, we will explore a range of essential concepts related to shapes, angles, and spatial reasoning. These principles lay the groundwork for more complex problem-solving techniques and help develop a deeper understanding of geometric relationships.
By examining key problems and their solutions, we aim to build a solid foundation for applying mathematical logic to various scenarios. Whether you’re looking to strengthen your skills or gain clarity on specific topics, this guide will offer clear explanations and practical steps for tackling common challenges.
Mastering these principles is crucial for success in this field, as they provide the tools needed to approach increasingly advanced problems with confidence. Understanding the underlying concepts is the first step toward becoming proficient in mathematical reasoning.
Geometry Chapter 8 Resource Book Answers
This section focuses on key problem-solving strategies and explanations that help break down complex tasks involving shapes, angles, and spatial reasoning. By examining various types of exercises, it becomes easier to see how fundamental concepts are applied to practical situations.
Through clear, step-by-step walkthroughs, this guide highlights the methods used to approach each type of problem effectively. The goal is to provide insight into common challenges and offer solutions that can be adapted to similar questions, enhancing both understanding and confidence in tackling advanced material.
Each solution is designed to emphasize important principles while demonstrating the most efficient ways to find results. The explanations aim to reinforce a deep understanding of mathematical relationships, ensuring that the problem-solving process becomes intuitive and manageable.
Key Concepts in Geometry Chapter 8
This section covers essential principles related to shapes, angles, and their properties, which form the basis of more advanced topics. Understanding these key ideas is critical for progressing in mathematical reasoning and tackling more complex exercises.
Core Ideas to Focus On

- Understanding the relationships between different types of figures.
- Learning how to calculate various properties like area, perimeter, and volume.
- Mastering the use of geometric formulas to solve problems efficiently.
- Recognizing the importance of proofs in validating geometric properties.
Important Techniques for Problem Solving
- Visualizing problems to simplify complex shapes and figures.
- Breaking down larger problems into smaller, manageable parts.
- Applying theorems and postulates to derive conclusions.
- Checking work for accuracy through logical steps and calculations.
By focusing on these core concepts and techniques, you’ll develop the skills needed to solve a wide range of related problems, ensuring a deeper understanding of the material and better problem-solving abilities overall.
How to Approach Geometry Problems

Successfully tackling problems that involve shapes and spatial relationships requires a systematic approach. By understanding the structure of each question, you can apply logical steps to find the most effective solution. This section outlines the strategies that can help you approach these types of problems with confidence.
Steps to Take Before Solving
- Carefully read the problem to identify key information and what is being asked.
- Sketch the figure or diagram if one is not provided to visualize the situation.
- Label all known values and variables clearly to keep track of important details.
- Determine which formulas or theorems are applicable to the problem at hand.
Effective Problem-Solving Techniques
- Break down the problem into smaller, manageable parts to avoid feeling overwhelmed.
- Work step by step, using logical reasoning to move from one stage to the next.
- Double-check calculations and results as you go to ensure accuracy.
- Review the problem once more after solving to confirm that the answer makes sense in the context of the question.
By following these methods, you’ll improve both your problem-solving skills and your understanding of the underlying principles, making each problem easier to tackle and solve.
Step-by-Step Solutions for Chapter 8
This section provides detailed solutions to problems involving shapes, measurements, and spatial reasoning. By following each solution step-by-step, you’ll gain a better understanding of how to apply relevant principles to solve various types of questions effectively.
Example 1: Solving for the Area of a Triangle

- Identify the base and height of the triangle from the given information.
- Use the formula for the area of a triangle: Area = (Base × Height) / 2.
- Substitute the known values into the formula and calculate the result.
- Double-check the units to ensure the area is expressed correctly (e.g., square units).
Example 2: Calculating the Volume of a Rectangular Prism
- Identify the length, width, and height of the prism.
- Use the volume formula: Volume = Length × Width × Height.
- Substitute the known values into the formula and perform the multiplication.
- Verify the result by checking that the units are consistent and appropriate (e.g., cubic units).
Following these clear, structured steps ensures accuracy and reinforces the logic behind each calculation. By applying this approach to similar problems, you can solve a wide variety of exercises with ease and confidence.
Understanding Geometric Figures in Chapter 8
In this section, we focus on the various shapes and structures that form the foundation of spatial reasoning. Each figure has distinct properties and relationships that help solve problems involving measurements, angles, and positions. A solid understanding of these figures is essential for working through complex exercises and achieving accurate solutions.
Recognizing key attributes such as sides, angles, and symmetry allows for the proper application of formulas and theorems. Whether dealing with triangles, quadrilaterals, or circles, being able to identify these properties helps simplify the problem-solving process. Moreover, understanding how different figures interact with one another in different contexts is vital for tackling more advanced tasks.
By mastering these fundamental shapes and their characteristics, you’ll be better equipped to apply the appropriate techniques and strategies to solve a wide range of problems effectively and efficiently.
Common Mistakes to Avoid in Geometry
When working with shapes, measurements, and spatial relationships, it’s easy to make errors that can lead to incorrect results. Recognizing and understanding these common mistakes can help you avoid them and improve your problem-solving skills. This section highlights some of the most frequent pitfalls and offers tips for overcoming them.
| Common Mistake | How to Avoid It |
|---|---|
| Confusing the formulas for area and perimeter | Remember that area measures the space inside a figure, while perimeter measures the distance around the figure. |
| Forgetting to check units | Always double-check that your units are consistent, and convert them if necessary before calculating. |
| Misinterpreting angles or sides in diagrams | Carefully review the diagram, label all known values, and verify that you’re working with the correct information. |
| Relying on visual estimation | Avoid making assumptions based on appearance–always use accurate calculations and measurements for precise results. |
By being mindful of these common errors and following clear, logical steps, you can ensure that your solutions are accurate and reliable. Avoiding these pitfalls is key to mastering the subject and improving overall performance.
Using Formulas Effectively in Chapter 8
Formulas are essential tools for solving problems involving measurements, areas, volumes, and other mathematical relationships. Knowing how to apply these formulas correctly is key to finding accurate solutions. In this section, we explore how to use various equations efficiently to tackle a range of tasks and avoid common mistakes.
The key to using formulas effectively lies in understanding their components and the context in which they are applied. Whether calculating the area of a polygon, the volume of a three-dimensional object, or solving for unknown angles, it’s important to first identify the correct formula for the task at hand.
Once the appropriate formula is chosen, ensure that all values are substituted correctly and that the units are consistent throughout the calculation. It’s also helpful to break down complex problems into smaller, manageable steps to ensure accuracy and clarity in each stage of the solution.
Mastering the use of formulas not only speeds up the problem-solving process but also builds confidence in applying mathematical concepts to real-world scenarios. With practice, using these formulas will become a natural and effective part of your problem-solving strategy.
Geometry Proofs Explained Simply
Proving mathematical statements is a fundamental aspect of problem-solving. While it might seem complex at first, breaking down proofs into logical steps can make the process clearer and more manageable. In this section, we will explore how to approach proofs effectively, step by step.
Understanding the Basics of a Proof

- A proof is a logical argument that establishes the truth of a statement.
- It is based on known facts, definitions, and previously proven theorems.
- Each step of a proof must follow logically from the previous one, ensuring consistency and accuracy.
Steps to Follow When Creating a Proof
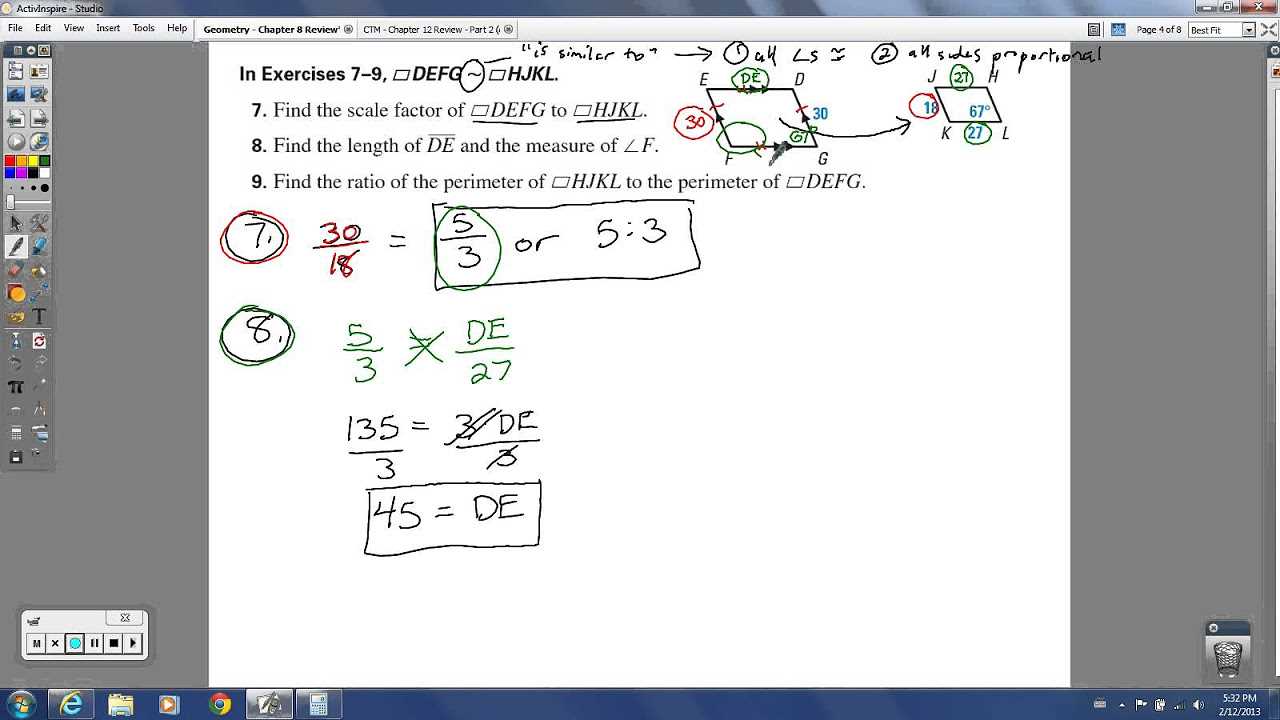
- Identify the statement you need to prove.
- List the given information and any relevant facts or theorems.
- Work through each step logically, using deductive reasoning to connect the given information to the conclusion.
- Ensure that each step is supported by a valid reason, whether it’s a definition, postulate, or previously proven result.
- Review the proof to confirm that all steps are clear, logical, and lead to the correct conclusion.
By following these steps and understanding the underlying structure of proofs, you will be able to approach them with confidence. Practice will further improve your ability to write clear, convincing proofs that demonstrate the validity of geometric concepts.
Visualizing Geometry Problems for Better Solutions
One of the most effective strategies for solving spatial problems is to visualize the scenario. By creating a mental image or drawing a diagram, you can better understand the relationships between different elements of the problem. This approach helps break down complex questions into simpler, more manageable components, leading to clearer insights and more accurate solutions.
Benefits of Visualization
- Helps clarify the problem by making abstract concepts more tangible.
- Enables you to identify key relationships between figures and elements quickly.
- Allows you to spot patterns or symmetries that might not be immediately obvious from the written problem.
- Improves accuracy by reducing the chances of misinterpreting the problem or making calculation errors.
How to Visualize Effectively

- Read the problem carefully and highlight important details such as dimensions, angles, or positions.
- Draw a clear diagram, labeling all known and unknown values.
- Use different colors or symbols to mark key relationships or connections between elements in the diagram.
- Look for symmetries or patterns in the figure that may help simplify calculations or reasoning.
By practicing visualization techniques and incorporating them into your problem-solving process, you can gain a deeper understanding of the task at hand, making it easier to arrive at the correct solution.
Advanced Techniques for Solving Geometry Questions
When facing more complex spatial problems, applying advanced strategies can make the difference between a challenging task and a straightforward solution. These techniques go beyond basic formulas and concepts, requiring a deeper understanding of relationships between shapes, angles, and dimensions. In this section, we explore several advanced approaches that can help simplify complicated questions and provide more efficient solutions.
Using Coordinate Geometry for Precision
Coordinate geometry allows for the precise placement of figures on a grid, which makes solving problems involving distances, slopes, and areas much easier. By translating geometric problems into algebraic equations, you can apply algebraic methods to find exact solutions.
- Plot key points and use the distance formula to calculate lengths.
- Apply the slope formula to determine the relationship between parallel and perpendicular lines.
- Use the area formula for triangles or polygons, based on coordinates.
Working with Transformations

Transformations such as translations, rotations, reflections, and dilations allow you to manipulate shapes in a controlled manner. By applying these transformations, you can explore properties like congruence, similarity, and symmetry, making it easier to analyze complex shapes and solve problems related to these concepts.
- Translate shapes to new positions to understand how distances and angles are preserved.
- Use rotations and reflections to identify symmetrical properties or solve for missing angles.
- Apply dilations to explore similarity and proportional relationships between figures.
Mastering these advanced techniques will not only help you solve problems more efficiently but also enhance your overall understanding of spatial reasoning and mathematical relationships. As you practice, you’ll gain the ability to approach even the most complex problems with confidence.
Importance of Practice in Geometry Mastery
Achieving proficiency in spatial reasoning and related mathematical skills requires more than just understanding the theory. Regular practice plays a crucial role in solidifying concepts and improving problem-solving abilities. The more problems you solve, the better you become at recognizing patterns, applying formulas, and mastering different techniques. This section will highlight why consistent practice is vital for mastering these concepts and improving overall performance.
Benefits of Regular Practice
- Improves retention of key concepts and formulas.
- Enhances problem-solving speed and accuracy.
- Builds confidence in tackling complex tasks.
- Helps identify common mistakes and areas that need improvement.
Effective Practice Strategies
- Start with simpler problems to build a strong foundation before progressing to more difficult ones.
- Review mistakes to understand where and why errors occurred, using them as learning opportunities.
- Practice under time constraints to improve both accuracy and speed.
- Work on a variety of problem types to develop versatility in your problem-solving approach.
| Practice Type | Benefit |
|---|---|
| Daily Problem Solving | Helps reinforce concepts and builds fluency. |
| Reviewing Mistakes | Helps identify weak areas and prevent repeated errors. |
| Timed Practice | Improves time management and speeds up solution process. |
By incorporating regular practice into your study routine, you can master key concepts and gain the confidence to approach complex problems with ease. Over time, this consistent effort leads to significant improvement in both understanding and application.
Tips for Studying Chapter 8

Studying mathematical concepts effectively requires more than just reading through the material; it involves active engagement with the content, consistent practice, and understanding the underlying principles. To tackle more advanced topics in this section, it’s essential to approach your study sessions strategically. In this section, we will outline some helpful strategies to maximize your learning experience and improve your grasp of key ideas.
Break Down Complex Problems

Start by dividing larger, more complex problems into smaller, manageable parts. This allows you to focus on individual aspects of the problem without feeling overwhelmed. By isolating different components, you can apply the appropriate methods and techniques to each part before combining them for the final solution.
Review Key Concepts and Formulas Regularly
- Revisit important formulas frequently to reinforce your understanding.
- Understand how and when to apply each formula in various situations.
- Create flashcards or summary notes to quickly review key points.
Additionally, regularly reviewing previously learned concepts helps maintain a strong foundation, making it easier to build upon new material. Don’t hesitate to revisit basic ideas that will help clarify more complex ones later.
Practice with a Variety of Problems
- Work on a mix of problems, from simple to advanced, to strengthen your skills.
- Include different types of questions, such as proofs, calculations, and real-world applications.
- Attempt problems without looking at solutions immediately to develop critical thinking skills.
By consistently applying these strategies and staying engaged with the material, you’ll be better prepared to tackle the content of this section and deepen your understanding of the subject.
Real-Life Applications of Geometric Concepts

Mathematical ideas are not confined to textbooks; they have practical applications in many fields of life. The concepts studied in this section can be applied to everyday situations, from architecture and engineering to art and technology. Understanding how these principles work in the real world can make learning more engaging and relevant. In this section, we’ll explore some common applications where these concepts play a crucial role.
Architecture and Construction

In construction, the layout of buildings, bridges, and roads relies heavily on the principles of shape, size, and space. Designers and engineers use these principles to create stable structures and efficient use of space. For example, understanding angles and proportions helps in the construction of roofs, staircases, and windows.
Technology and Computer Graphics
The digital world also benefits from spatial reasoning. Computer programmers and graphic designers use these concepts to create 3D models, animations, and virtual simulations. Whether it’s designing video game environments or mapping out virtual landscapes, geometric knowledge is key to building accurate and realistic visual representations.
Art and Design
In the world of visual arts, artists have used geometric shapes and principles for centuries. From the ancient Greeks to modern-day designers, understanding symmetry, perspective, and proportion is essential for creating visually appealing works. Artists use geometric concepts to organize space, create depth, and maintain balance in their compositions.
By seeing how these concepts function in practical contexts, it’s easier to appreciate their value beyond the classroom. Whether in designing buildings or creating digital art, these mathematical tools are integral to many professional fields.
How to Check Your Solutions
After working through mathematical problems, it’s essential to verify your solutions to ensure their accuracy. This process involves reviewing each step of your work, comparing it with established principles, and applying checks to confirm your final result. In this section, we’ll discuss effective methods to verify your results and catch common errors before finalizing your solutions.
Review Each Step Methodically
Start by carefully reviewing each step you took to solve the problem. Ensure that all logical operations were performed correctly and that you didn’t skip any crucial steps. Double-check formulas and ensure the appropriate ones were used for the given problem. If you used any shortcuts, verify that they are applicable to the specific situation.
Use Alternative Methods
If possible, approach the problem from a different angle. This could involve using a different method or formula to solve the same problem. For example, if you solved an equation using algebraic manipulation, try verifying it with a geometric or visual approach. This cross-checking helps you confirm the consistency and accuracy of your result.
Check Units and Measurements
- Ensure that all measurements are in the correct units.
- Verify that any conversions between units were done properly.
- Double-check your final answer’s units to ensure consistency with the problem’s requirements.
By applying these strategies, you can feel more confident in the accuracy of your solutions and avoid mistakes that might affect your overall understanding and problem-solving ability.
Key Theorems and Postulates in Chapter 8
Understanding fundamental principles is essential when solving complex problems. In this section, we will explore some of the most important theorems and postulates that form the foundation for reasoning and proof construction. These principles help in simplifying the process of solving various types of problems by offering clear, established rules that can be applied to different situations.
Here are some of the key theorems and postulates that are widely used in problem-solving:
| Theorem/Postulate | Description |
|---|---|
| Parallel Postulate | States that if two lines are cut by a transversal and the interior angles on the same side of the transversal are supplementary, then the lines are parallel. |
| Angle-Sum Theorem | In any triangle, the sum of the interior angles is always 180 degrees. |
| Vertical Angles Theorem | States that when two lines intersect, the angles formed opposite each other are congruent. |
| Congruence Postulate | Two triangles are congruent if their corresponding sides and angles are equal in measure. |
By thoroughly understanding and applying these theorems and postulates, students can confidently tackle problems that require logical reasoning and a solid grasp of geometric relationships. These principles serve as powerful tools that allow for the simplification and solving of geometric problems across various contexts.
How Geometry Chapter 8 Prepares for Further Studies
The skills and concepts learned in this section form a crucial foundation for more advanced mathematical studies. By mastering fundamental principles, students can approach more complex subjects with confidence and clarity. This section introduces techniques and problem-solving methods that are not only important for higher-level coursework but are also applicable in various professional fields such as engineering, architecture, and physics.
Building Logical Thinking and Problem-Solving Skills
One of the key areas of focus in this section is developing logical reasoning. As students solve problems step by step, they learn to approach challenges systematically. This methodical thinking prepares them for more intricate topics that require a clear understanding of relationships between different elements and the ability to apply abstract concepts effectively.
Applications in Advanced Mathematical Topics
In subsequent studies, students will encounter more complex ideas such as calculus, linear algebra, and trigonometry. The principles from this section, particularly those dealing with spatial reasoning and transformations, lay the groundwork for these more advanced subjects. Mastering the concepts here ensures that students can tackle more sophisticated topics with ease, as they already have a strong grasp of the underlying mathematical structures.
Overall, this section serves as a vital stepping stone for future academic endeavors, enhancing both problem-solving abilities and mathematical comprehension, setting the stage for success in higher education and beyond.