
In this section, we will focus on some of the fundamental principles that form the foundation of mathematical problem-solving. These concepts are essential for mastering techniques that involve both equations and their graphical representations. By diving into the core strategies, you will gain the confidence to tackle more complex problems as you advance in your studies.
The materials presented here are designed to help you strengthen your skills in handling different types of equations and inequalities. We will explore various methods, each offering unique approaches to solving problems, ensuring that you are equipped to handle a wide range of mathematical challenges. Practice and understanding are key to success, and through these exercises, you will refine your ability to think critically and methodically.
Whether you’re preparing for upcoming tests or simply looking to sharpen your problem-solving abilities, this guide provides the tools necessary to succeed. With careful attention to detail and step-by-step guidance, you will learn how to break down problems and apply the appropriate strategies to find solutions. Mastery of these skills will open the door to more advanced topics in mathematics and beyond.
Algebra 1 Chapter 6 Review Answers
This section is designed to help you strengthen your problem-solving skills by providing solutions to key exercises. By breaking down each problem step-by-step, you will gain a deeper understanding of the methods and strategies used to solve equations and inequalities. Mastery of these concepts is essential for progressing in mathematics.
Let’s explore the different types of problems you might encounter:
- Linear equations and their solutions
- Systems of equations and methods for solving them
- Graphing lines and interpreting slopes and intercepts
- Solving and graphing inequalities
- Word problems involving linear relationships
Each exercise in this section follows a logical structure, showing how to approach problems and work through them efficiently. By practicing these steps, you will learn how to identify patterns, apply appropriate methods, and arrive at correct solutions.
Here are the steps typically involved in solving these problems:
- Read the problem carefully to understand the given information.
- Choose the appropriate method (substitution, elimination, graphing, etc.) for the problem.
- Perform the necessary calculations, ensuring each step follows logically from the previous one.
- Check your solutions to ensure they satisfy the original conditions of the problem.
- Review any mistakes and understand why they occurred to avoid repeating them in the future.
Through consistent practice and by reviewing the solutions provided, you will develop a solid foundation for tackling more advanced topics in the future.
Key Concepts in Algebra 1 Chapter 6
This section covers the foundational principles necessary for solving equations and inequalities. Understanding these concepts is crucial for developing the skills required to handle more complex mathematical problems. By focusing on the core methods and strategies, you will gain the tools to effectively approach a variety of problem types.
Among the essential ideas explored here are:
- Understanding the relationship between variables and constants
- Methods for solving systems of equations
- Graphing linear functions and analyzing their properties
- Identifying the slope and intercepts of lines
- Solving and interpreting inequalities
These concepts are not only central to the current material but also serve as the building blocks for future mathematical topics. By grasping these fundamental techniques, you’ll improve your problem-solving efficiency and increase your overall confidence in mathematics.
Understanding Linear Equations and Inequalities
In this section, we explore the fundamentals of solving relationships between variables. These mathematical expressions are essential for describing various real-world situations and can be solved through different techniques. Mastery of these methods is key for tackling both simple and complex problems efficiently.
Linear Equations
A linear equation represents a straight line when graphed. It typically involves variables raised to the first power and can be solved using various methods. The main goal is to find the value(s) of the unknowns that satisfy the equation.
- Identifying the general form of a linear equation: Ax + B = C
- Solving for the unknown by isolating the variable
- Checking the solution by substituting back into the original equation
Inequalities
Inequalities describe ranges of possible values for the variables. Unlike equations, they provide multiple solutions, represented by shaded areas on a graph. Solving inequalities involves finding a range of values that satisfy the given conditions.
- Understanding the signs: >, <, >=, <=
- Solving inequalities similarly to equations, with adjustments for multiplication or division by negative numbers
- Graphing solutions on a number line or coordinate plane
Both linear equations and inequalities are essential tools in mathematical problem-solving. By practicing these techniques, you will be better equipped to handle various types of problems and understand their real-world applications.
Solving Systems of Equations
This section focuses on methods for solving sets of equations that involve multiple unknowns. These systems can represent real-life scenarios such as determining the point of intersection between two lines. Solving them efficiently requires applying different techniques depending on the structure of the system.
Substitution Method
The substitution method involves solving one equation for one variable and then substituting that expression into the second equation. This approach simplifies the system to a single equation with one variable, which can then be solved.
- Choose one equation and isolate one variable.
- Substitute the expression for that variable into the other equation.
- Solve for the remaining variable.
- Substitute the value back into the original equation to find the first variable.
Elimination Method
The elimination method aims to eliminate one variable by adding or subtracting the equations. This results in a simpler equation with only one variable to solve. Once one variable is found, it can be substituted back into one of the original equations to find the other variable.
- Multiply or divide the equations to align the coefficients of one variable.
- Add or subtract the equations to eliminate that variable.
- Solve the resulting equation for the remaining variable.
- Substitute the value back into one of the original equations to solve for the other variable.
Both methods are useful for different types of systems. The choice of method depends on the structure of the equations and the complexity of the problem. Mastering both approaches will provide flexibility in solving systems quickly and accurately.
Graphing Linear Functions Step by Step
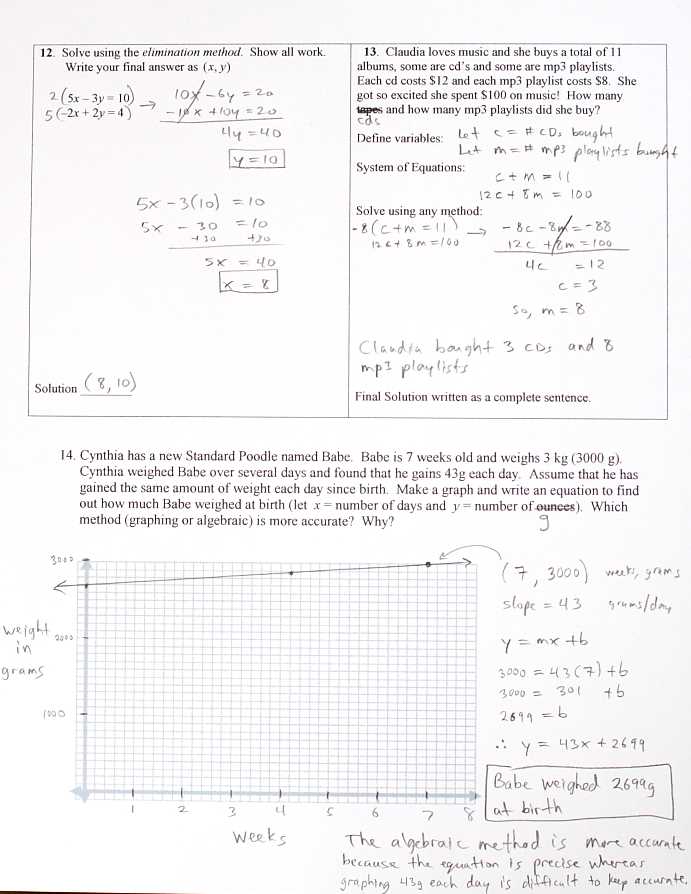
Graphing linear equations involves representing relationships between two variables on a coordinate plane. By plotting points that satisfy the equation and connecting them, you can visualize how the variables change relative to each other. This process is key for understanding the behavior of linear relationships.
Identifying the Slope and Intercept
To graph a linear equation, the first step is to identify the slope and y-intercept from the equation in slope-intercept form: y = mx + b. Here, m represents the slope, and b represents the y-intercept, which is the point where the line crosses the y-axis.
- The slope indicates the steepness and direction of the line (positive slope means the line rises, negative means it falls).
- The y-intercept gives the starting point of the line on the vertical axis.
Plotting the Line
Once you have the slope and y-intercept, follow these steps to plot the graph:
- Start by marking the y-intercept on the graph.
- Use the slope to find the next point by moving up or down based on the numerator and left or right based on the denominator.
- Plot a second point, then draw a straight line through both points.
- Extend the line in both directions to complete the graph.
By following these steps, you can accurately represent any linear equation on a graph, allowing you to better understand the relationship between the variables and their graphical representation.
Exploring Slope and Y-Intercept
Understanding the slope and y-intercept is fundamental when working with linear relationships. These two components help define the direction and position of a line on a coordinate plane. By analyzing them, you can predict the behavior of the relationship and graph the equation with ease.
The slope and y-intercept are key elements in the equation of a line, often written in the form y = mx + b. Here, m represents the slope, and b represents the y-intercept. These values allow us to fully describe the line’s characteristics.
Slope: The Rate of Change
The slope measures how much one variable changes in relation to the other. It describes the steepness and direction of a line. A positive slope indicates that as one variable increases, the other also increases, whereas a negative slope indicates the opposite.
- Positive slope: The line rises from left to right.
- Negative slope: The line falls from left to right.
- Slope formula: m = (y₂ – y₁) / (x₂ – x₁) describes the change in y over the change in x between two points.
Y-Intercept: The Starting Point
The y-intercept is the point where the line crosses the vertical axis. This value tells us the output of the equation when the input (x) is zero. Understanding the y-intercept allows you to set a starting point for the graph and determine where the line will begin.
- The y-intercept is represented by b in the equation y = mx + b.
- It is the value of y when x = 0.
- In graphical terms, it is the point where the line intersects the y-axis.
By combining the slope and y-intercept, you can easily graph any linear equation and interpret its meaning. These two components provide a clear picture of how the variables relate to each other and how the line behaves across the coordinate plane.
Solving Word Problems Using Algebra
Word problems are an essential part of understanding mathematical relationships in real-life contexts. These problems require translating everyday situations into mathematical equations, which can then be solved using a variety of techniques. By breaking down the text and identifying the variables and operations involved, you can turn a complex problem into a manageable equation.
The key to solving word problems is to carefully read the problem, identify what is being asked, and assign variables to the unknowns. From there, you can create equations that represent the relationships described in the problem. Once the equations are set up, you can solve them using basic arithmetic or more advanced methods, depending on the complexity of the situation.
Here are some steps to follow when tackling word problems:
- Read the problem carefully: Understand the context and identify the unknowns.
- Assign variables: Label the unknowns with variables, such as x or y.
- Set up equations: Translate the relationships in the problem into mathematical expressions.
- Solve the equations: Use appropriate methods, like addition, subtraction, multiplication, or division, to solve for the unknowns.
- Check the solution: Make sure your answer makes sense in the context of the problem.
By following these steps, you can solve word problems effectively and gain a deeper understanding of how mathematical principles apply to real-world scenarios. With practice, these types of problems become easier to interpret and solve.
Understanding the Substitution Method
The substitution method is a technique used to solve systems of equations by isolating one variable in one equation and substituting that expression into the other equation. This method simplifies the system to one equation with a single variable, making it easier to solve. Once the value of one variable is found, it can be substituted back into the original equation to find the value of the other variable.
Steps for Solving Using Substitution
Follow these steps to apply the substitution method to a system of equations:
- Isolate a variable: Choose one of the equations and solve it for one variable (e.g., solve for x or y).
- Substitute the expression: Substitute the expression found for the isolated variable into the other equation.
- Solve the simplified equation: Now, you will have a single equation with only one variable. Solve for that variable.
- Substitute back: Once the value of the first variable is determined, substitute it back into one of the original equations to solve for the second variable.
Example of Substitution
Consider the following system of equations:
- 2x + 3y = 12
- x – y = 3
To use the substitution method:
- First, solve the second equation x – y = 3 for x: x = y + 3.
- Now, substitute x = y + 3 into the first equation: 2(y + 3) + 3y = 12.
- Simplify and solve for y: 2y + 6 + 3y = 12, which simplifies to 5y = 6, so y = 6/5.
- Finally, substitute y = 6/5 back into x = y + 3 to find x = 6/5 + 3.
- The solution is x = 21/5 and y = 6/5.
This method provides an organized and systematic approach to solving systems of equations. It is particularly useful when one of the equations is easily solvable for one variable.
Elimination Method Explained
The elimination method is a technique used to solve systems of equations by eliminating one variable at a time, making it easier to solve for the remaining variable. This method involves adding or subtracting the equations in such a way that one of the variables cancels out, leaving you with a simpler equation that can be solved directly. Once one variable is determined, you can substitute its value into one of the original equations to find the other variable.
Steps for Using the Elimination Method
To solve a system of equations using the elimination method, follow these steps:
- Align the equations: Write both equations in standard form (Ax + By = C), aligning the variables.
- Multiply to match coefficients: If necessary, multiply one or both of the equations by a constant to ensure the coefficients of one variable match in both equations.
- Add or subtract the equations: Add or subtract the equations to eliminate one variable. This will result in a single equation with one variable.
- Solve the resulting equation: Solve for the remaining variable.
- Substitute the value: Substitute the value of the solved variable into one of the original equations to find the value of the other variable.
Example of Elimination
Consider the following system of equations:
- 3x + 4y = 18
- 2x – 4y = 2
To use the elimination method:
- First, notice that the coefficients of y are opposites (4 and -4), so we can eliminate y directly by adding the two equations.
- Add the equations: (3x + 4y) + (2x – 4y) = 18 + 2. The y terms cancel out, and we are left with 5x = 20.
- Now, solve for x: x = 20 / 5 = 4.
- Substitute x = 4 into one of the original equations, for example, 3x + 4y = 18: 3(4) + 4y = 18, which simplifies to 12 + 4y = 18.
- Solve for y: 4y = 6, so y = 6 / 4 = 3/2.
The solution to the system of equations is x = 4 and y = 3/2.
The elimination method is highly effective when the system is set up in such a way that one variable can be easily eliminated, allowing for quicker solutions compared to other methods like substitution.
Working with Functions and Their Graphs

Understanding how mathematical relationships are represented visually is a crucial skill. Functions describe how one quantity changes in relation to another, and their graphs provide a visual representation of this relationship. By analyzing the graph of a function, you can gain valuable insights into its behavior, such as where it intersects the axes, whether it increases or decreases, and how steeply it rises or falls.
Graphs of functions allow you to see the effects of different inputs on outputs, which is helpful for both solving problems and interpreting data. The x-axis typically represents the independent variable, while the y-axis represents the dependent variable. A function’s graph helps identify key features such as slope, intercepts, and intervals where the function increases or decreases.
Key Features of Function Graphs
When working with graphs, there are several key features to identify:
- Intercepts: These are the points where the graph crosses the axes. The x-intercept occurs where the graph crosses the x-axis, and the y-intercept occurs where it crosses the y-axis.
- Slope: This represents the steepness of the graph. A positive slope means the function increases, while a negative slope means it decreases. The slope can be calculated by finding the ratio of vertical change to horizontal change between two points.
- Domain and Range: The domain refers to all possible input values (x-values) for which the function is defined, while the range refers to all possible output values (y-values) that the function can produce.
- Behavior: Understanding whether the function is increasing, decreasing, or constant over certain intervals can provide insights into how the values change as the input changes.
Graphing a Linear Function

Graphing a linear function involves plotting points that satisfy the equation of the function. For example, consider the equation:
- y = 2x + 3
To graph this function:
- Start by identifying the y-intercept, which is 3 (the point (0, 3) on the graph).
- Next, use the slope of 2 to find another point. The slope of 2 means that for every 1 unit you move to the right (increase in x), you move up 2 units (increase in y). This gives you another point, (1, 5).
- Plot these points on a graph, then draw a straight line through them. This line represents the relationship defined by the function.
By analyzing the graph, you can easily identify the slope and intercept, as well as the general direction of the function.
Graphing functions provides a clear visual representation of their behavior, which is invaluable in understanding mathematical relationships and solving real-world problems.
Mastering Multi-Step Equations
Solve complex problems effectively by mastering equations that require multiple operations to find the unknown. These problems often combine addition, subtraction, multiplication, division, and sometimes even distribution of terms. The key to solving them is applying a systematic approach and following the order of operations.
Working through multi-step problems involves isolating the variable step by step while keeping the equation balanced. By simplifying each part of the equation, you can gradually eliminate terms until you reach the solution. This method not only improves problem-solving skills but also strengthens the ability to work with a wide variety of mathematical expressions.
Step-by-Step Process
To solve multi-step problems, follow these general steps:
- Distribute: If there are parentheses, begin by distributing any factors across the terms inside them.
- Combine like terms: Group and simplify terms that contain the same variable or constant to make the equation easier to solve.
- Isolate the variable: Use addition or subtraction to move constants to one side, then divide or multiply to isolate the variable.
- Check your solution: Once you have a value for the variable, substitute it back into the original equation to ensure that both sides are equal.
Example Problem

Consider the equation:
3(x + 4) – 2 = 4x + 6
To solve this, first distribute:
- 3(x + 4) becomes 3x + 12, so the equation becomes: 3x + 12 – 2 = 4x + 6.
Next, combine like terms on the left side:
- 3x + 10 = 4x + 6.
Now, isolate the variable by subtracting 3x from both sides:
- 10 = x + 6.
Finally, subtract 6 from both sides:
- 4 = x.
The solution is x = 4. You can check your work by substituting x = 4 back into the original equation to verify that both sides are equal.
Mastering multi-step problems opens the door to more advanced concepts and strengthens your problem-solving abilities. With consistent practice, you will gain confidence in tackling even more complex equations.
Tips for Solving Inequalities Efficiently

Solving inequalities requires a strategic approach to ensure accuracy and efficiency. While similar to solving equations, inequalities involve finding a range of possible values rather than a single solution. To solve them successfully, it’s important to follow specific rules and apply them consistently, keeping track of key concepts such as reversing inequality signs when multiplying or dividing by negative numbers.
Here are some essential tips for solving inequalities efficiently:
| Tip | Description |
|---|---|
| 1. Keep the inequality balanced | Similar to equations, you must perform the same operation on both sides of the inequality to maintain balance. |
| 2. Reverse the sign when multiplying/dividing by a negative number | If you multiply or divide by a negative number, make sure to flip the inequality sign. This is a critical step to avoid mistakes. |
| 3. Combine like terms | Simplify the inequality by combining terms that are similar (e.g., constants and coefficients), which makes the inequality easier to handle. |
| 4. Isolate the variable | Just like equations, isolating the variable is key. Use addition, subtraction, multiplication, or division to get the variable on one side. |
| 5. Test the solution | After solving, it’s essential to check the solution by substituting values into the original inequality to see if the result holds true. |
By applying these tips, solving inequalities becomes a more straightforward and systematic process. Let’s now walk through a simple example to illustrate these steps in action.
Consider the inequality:
2x – 5 > 9
Follow the steps below:
- First, add 5 to both sides: 2x > 14.
- Next, divide by 2: x > 7.
The solution to this inequality is any number greater than 7. Testing with values like 8, 9, or even 10 will satisfy the inequality.
Mastering these strategies will help you solve inequalities more effectively, preparing you for even more complex challenges ahead.
Common Mistakes to Avoid in Chapter 6
While working through problems in this section, it’s easy to make a few errors that can lead to incorrect solutions. These mistakes are often subtle and can easily be overlooked, but they can affect the overall understanding and accuracy of the process. Being aware of common pitfalls and learning how to avoid them is essential for mastering the material and achieving success in the topic.
Here are some of the most frequent mistakes that students make and tips on how to avoid them:
- Forgetting to reverse the inequality sign when multiplying or dividing by a negative number. This is one of the most critical rules to follow, as it can completely change the meaning of the inequality.
- Mixing up addition and subtraction with multiplication and division when isolating variables. Be sure to perform each operation carefully, and don’t rush through these steps.
- Overlooking the need to combine like terms before proceeding with more complex steps. Always simplify the equation or inequality first to avoid errors down the line.
- Misinterpreting the problem’s direction. Whether solving for an unknown variable or graphing an equation, ensure you understand what the problem is asking. Double-checking the problem statement can save time and frustration.
- Skipping the verification step after solving. It’s important to always substitute the solution back into the original expression to verify its accuracy, especially when solving word problems.
- Not understanding the relationship between the slope and y-intercept when graphing equations. Remember that the slope determines the steepness, and the y-intercept marks where the graph crosses the y-axis.
By being mindful of these mistakes and taking care to follow the correct steps, you can avoid common errors and improve your understanding of the concepts. The more practice you get, the easier it will be to navigate through the material without falling into these traps.
Practical Applications of Linear Equations
Linear equations are not only foundational in mathematics, but they also have a wide range of practical uses in real-world situations. Whether you are budgeting, planning a business strategy, or analyzing data trends, understanding how to set up and solve these equations is essential. These equations help model various phenomena and make predictions based on given information, providing valuable insight into problem-solving across different fields.
Here are some of the key areas where linear equations are applied:
- Budgeting and Finance: Linear equations are often used to create financial models. For example, you can use them to calculate expenses and income over time or determine how much you need to save to meet specific goals.
- Business and Economics: Companies use linear equations to predict profits, set prices, and manage costs. They help model supply and demand, and can even be used to forecast future sales trends based on current data.
- Construction and Engineering: When planning construction projects, linear equations can help with determining materials needed, calculating costs for labor, and estimating project timelines based on fixed parameters.
- Science and Medicine: In biology, chemistry, and physics, linear equations are used to model rates of change, such as the growth of a population or the speed of a reaction. They are also used in medical fields to determine dosages or to model certain disease patterns.
- Data Analysis and Statistics: Linear equations are essential for analyzing data trends. For example, regression analysis uses linear equations to predict future values based on historical data.
By learning how to solve and apply these equations, you can better understand and navigate the world around you, making informed decisions and solving real-life problems with confidence.
Reviewing Key Formulas
Understanding and mastering important formulas is crucial for solving mathematical problems efficiently. Whether you are working with equations, inequalities, or graphs, these formulas provide a foundation for tackling various types of problems. Reviewing and memorizing these essential equations can significantly improve your ability to solve tasks quickly and accurately.
Below is a summary of key formulas that you should be familiar with:
| Formula Name | Formula | Description |
|---|---|---|
| Slope Formula | m = (y₂ – y₁) / (x₂ – x₁) | Used to calculate the slope of a line given two points (x₁, y₁) and (x₂, y₂). |
| Point-Slope Form | y – y₁ = m(x – x₁) | A way to express the equation of a line when the slope and a point on the line are known. |
| Slope-Intercept Form | y = mx + b | Represents a linear equation, where m is the slope and b is the y-intercept. |
| Standard Form | Ax + By = C | A general form for linear equations, where A, B, and C are constants. |
| Quadratic Formula | x = (-b ± √(b² – 4ac)) / 2a | Used to find the roots of a quadratic equation ax² + bx + c = 0. |
These formulas are indispensable for solving various problems in mathematics. By understanding their application, you can tackle a wide range of equations and make more informed decisions when analyzing data or graphs.
Preparing for the Test
Proper preparation is essential for success in any mathematical assessment. To excel in this test, it is important to focus on understanding the key concepts, mastering the methods, and practicing problems that resemble the ones you will encounter. Strengthening your skills in solving equations, analyzing graphs, and applying various formulas will ensure that you are well-prepared.
Here are some strategies to help you prepare effectively:
Key Areas to Focus On
- Understanding different forms of linear equations and how to convert between them.
- Solving systems of equations using different methods like substitution and elimination.
- Mastering the interpretation and graphing of linear relationships.
- Recognizing the importance of the slope and y-intercept in equations and their graphs.
- Practicing word problems that involve real-life applications of mathematical concepts.
Practice Problems

Working through sample problems can significantly improve your understanding and boost your confidence. Below is a list of problem types you should practice:
| Problem Type | Focus Area | Suggested Practice |
|---|---|---|
| Linear Equations | Solving single-variable equations | Solve for x in equations like 2x + 5 = 11 |
| Systems of Equations | Using substitution or elimination | Solve for both x and y in equations like 2x + y = 7 and x – y = 1 |
| Graphing | Plotting points and lines | Graph lines using the slope-intercept form y = mx + b |
| Word Problems | Real-life applications | Write and solve equations based on scenarios, like calculating the cost of items. |
By practicing regularly and focusing on these core concepts, you will be prepared to perform well and approach each problem with confidence.