
Participating in a global mathematical contest offers students an exciting opportunity to test their skills and sharpen their problem-solving abilities. These competitions are designed to challenge young minds, pushing them to think critically and apply creative solutions to complex questions. Every year, the event attracts participants from various countries, each eager to showcase their talent and improve their logical reasoning.
The focus of these contests is not just on basic arithmetic, but on a wide range of concepts that test one’s understanding of abstract mathematics. From geometry to algebra, and even number theory, the tasks aim to stimulate a deep understanding of mathematical principles and encourage strategic thinking. In addition to fostering individual growth, these contests provide valuable feedback that helps students identify their strengths and areas for improvement.
In this section, we explore the solutions and techniques used to approach the problems from one of the recent years. By reviewing key questions and their corresponding explanations, participants can gain a clearer understanding of the reasoning behind each step. This will not only help them in their future endeavors but also improve their overall performance in similar events.
Mathematical Contest Solutions Overview
In this section, we provide an in-depth exploration of the solutions to some of the key problems presented in one of the most recognized global mathematical contests. The goal is to break down the logical steps and strategies used to arrive at correct conclusions, helping participants understand the reasoning behind each response. By analyzing these problems and their corresponding solutions, students can enhance their skills and gain insights into problem-solving techniques that are crucial for success in similar future challenges.
Understanding the Problem-Solving Approach
The primary focus of this review is to offer a clear, step-by-step breakdown of how to approach and solve each problem effectively. Here are some key strategies that can help in tackling complex tasks:
- Analyze the Question: Carefully read and break down the problem to ensure complete understanding.
- Identify Key Concepts: Look for underlying mathematical principles that apply to the question.
- Consider Alternative Methods: Think about different ways to approach the problem to find the most efficient solution.
- Practice Logical Deduction: Use critical thinking to draw conclusions from the given information.
Detailed Breakdown of Sample Problems

To make the learning process more engaging and effective, we’ll review some of the sample problems and their solutions. This includes explaining how specific techniques and strategies were used to solve challenging questions. The process involves:
- Problem Interpretation: Understanding the key elements and what is being asked.
- Solution Pathway: Step-by-step guidance on how the answer is derived.
- Final Verification: Ensuring the solution meets all conditions and is logically sound.
By following this breakdown, students can gain a comprehensive understanding of the problem-solving process, which can be applied to future contests and mathematical challenges.
Understanding the Contest Format
The structure of a global mathematical competition is designed to challenge participants with a range of problems that test both their computational skills and their ability to think critically. The format typically includes various types of questions, each increasing in difficulty, that require different strategies and approaches. Understanding the format is key to preparing effectively and performing well in the contest.
Types of Questions
The competition consists of multiple-choice questions, with each question offering several options. The format encourages participants to apply their knowledge in a time-sensitive environment while focusing on accuracy and logical reasoning. Here is a breakdown of how the questions are typically organized:
| Level | Difficulty | Types of Questions |
|---|---|---|
| Level 1 | Easy | Basic arithmetic and simple logic puzzles |
| Level 2 | Medium | Algebra, number theory, and pattern recognition |
| Level 3 | Hard | Advanced geometry, combinatorics, and abstract reasoning |
Time Management and Strategy
Participants must carefully manage their time throughout the contest, as the clock is ticking on each set of questions. Understanding the time constraints and pacing oneself is vital for success. The ability to quickly assess the difficulty of each question and decide whether to attempt it or skip it for later is a skill that can be honed through practice and familiarity with the competition’s format.
Importance of Preparing for the Competition
Preparation plays a crucial role in achieving success in any competitive event. When it comes to mathematical challenges, early and focused practice can significantly improve problem-solving abilities, boost confidence, and help participants develop the necessary skills to perform well under time pressure. Proper preparation allows students to familiarize themselves with the question formats, identify areas for improvement, and build mental stamina for complex tasks.
Building Strong Problem-Solving Skills

One of the primary benefits of preparation is the development of problem-solving skills. Regular practice enables participants to approach questions methodically, improving their ability to break down complex problems into manageable steps. It also helps strengthen logical thinking and creativity, which are essential for finding efficient solutions. As participants encounter a variety of question types, they learn to apply different mathematical techniques and recognize patterns that lead to faster solutions.
Boosting Confidence and Reducing Anxiety
Familiarity with the competition’s format and the types of problems encountered reduces anxiety and boosts confidence. When participants know what to expect, they are less likely to feel overwhelmed by challenging questions. Consistent practice helps them build resilience and stay focused, even when faced with difficult tasks. Being prepared is key to overcoming any stress that may arise during the event.
Exam Structure of the 2006 Competition

The structure of the event is designed to challenge participants at various skill levels while encouraging critical thinking and logical reasoning. Each segment of the exam is carefully crafted to test different aspects of mathematical ability, ranging from basic calculations to advanced problem-solving techniques. Understanding the layout of the exam is essential for participants to strategize and allocate their time effectively during the competition.
Question Distribution and Levels
The exam is divided into multiple sections, each progressively more difficult. Participants face a series of questions that are categorized by increasing complexity. The questions are typically divided into three main levels, designed to test a range of abilities, from basic arithmetic to more advanced topics such as geometry and number theory.
- Level 1: Basic problems that focus on fundamental skills such as arithmetic and simple logic.
- Level 2: Intermediate questions that require the application of algebra, patterns, and basic geometric principles.
- Level 3: Advanced problems that challenge participants with complex reasoning, abstract concepts, and multi-step solutions.
Time Allocation and Strategy
Time management is a key aspect of the competition. Each section is allotted a specific time limit, encouraging participants to work efficiently and make decisions on which questions to prioritize. Knowing the structure allows competitors to pace themselves and avoid spending too much time on more challenging problems, ensuring they can complete the entire exam within the given time frame.
How to Approach Competition Questions
Successfully tackling questions in a mathematical competition requires more than just knowledge of formulas and concepts. It involves a strategic approach, a clear understanding of the problem, and effective time management. Developing the ability to analyze each question carefully and systematically is key to achieving optimal results. Here are some essential steps to follow when approaching competition questions.
- Read the Problem Carefully: Before attempting to solve a problem, take the time to read it thoroughly. Ensure you understand what is being asked and identify any key information provided.
- Break Down the Question: Divide the problem into smaller, more manageable parts. This will make it easier to identify relevant concepts and methods needed to find the solution.
- Look for Patterns: Often, problems in competitions involve recognizing patterns or relationships. Look for trends in the numbers, shapes, or variables that might help simplify the task.
- Eliminate Incorrect Options: If the exam involves multiple-choice questions, use the process of elimination to rule out obviously incorrect answers. This increases your chances of selecting the correct one.
- Manage Your Time: Pay attention to the time limit for each section. Don’t spend too much time on a single problem; if you’re stuck, move on and return to it later if time allows.
By practicing these strategies, participants can improve their problem-solving efficiency and increase their chances of performing well in the competition. With time and experience, approaching difficult questions becomes a more intuitive process.
Key Strategies for Solving Problems
When faced with complex problems, especially in a competitive setting, it’s essential to approach them with the right mindset and set of techniques. Developing a systematic approach not only helps in finding the correct solution but also in managing time efficiently. By honing specific problem-solving strategies, participants can improve both their accuracy and speed during challenges.
Understanding the Problem Fully
Before diving into calculations or trying to find an answer, it’s crucial to fully comprehend the problem at hand. Break the question down into its core components and identify key data points. A clear understanding of what is being asked will guide you in selecting the most appropriate method to solve it.
- Identify Known and Unknown Variables: Make a list of all given information and what you need to find.
- Clarify Relationships: Determine how the elements in the problem are connected or how they relate to one another.
- Look for Hidden Clues: Often, the problem will provide indirect hints that can simplify the solution.
Utilizing Logical and Creative Techniques
Once the problem is understood, using logical reasoning and creative techniques can help find a path to the solution. This may involve applying familiar formulas, creating diagrams, or simplifying complex expressions.
- Use Diagrams or Visuals: Drawing a picture or graph can sometimes reveal patterns or relationships that aren’t immediately obvious.
- Check for Symmetry or Patterns: Identifying repeating elements in the problem may help simplify the work.
- Work Backwards: Sometimes starting from the desired result and working backwards can be a more efficient approach.
By mastering these strategies, individuals can enhance their problem-solving ability, leading to better performance in competitive environments.
Common Mistakes in Competitions

During challenging problem-solving events, even the most experienced participants can make mistakes that hinder their performance. Understanding the common errors made by others can help you avoid them and improve your chances of success. These mistakes often stem from misunderstandings of the questions, rushed calculations, or not fully applying problem-solving techniques. By being aware of these pitfalls, you can approach each problem more carefully and with greater accuracy.
- Misinterpreting the Question: One of the most common mistakes is misunderstanding the problem or missing key details. Reading the question carefully and ensuring you know what is being asked can prevent this error.
- Rushing Through Problems: Time pressure can lead to hasty decisions, such as making quick calculations without fully considering all the possibilities. Taking the time to think through each step is crucial to avoid careless mistakes.
- Skipping Steps: Trying to solve a problem too quickly may lead to skipping essential steps in the solution process. It’s important to follow a logical progression and check each part of the solution before proceeding.
- Overcomplicating Solutions: Sometimes, in an effort to find a complex solution, participants overthink the problem. The simplest approach is often the best, so focusing on basic principles can help avoid unnecessary confusion.
- Incorrect Use of Formulas: Misapplying mathematical formulas or incorrectly interpreting mathematical concepts can lead to incorrect answers. It’s essential to familiarize yourself with the correct formulas and know when to apply them.
- Failing to Check Answers: Neglecting to review your answers is a common mistake. Double-checking your calculations and ensuring that your solution makes sense can help catch errors before submission.
Avoiding these mistakes requires practice, careful attention to detail, and a methodical approach to each question. By staying mindful of these common errors, participants can improve their performance and achieve better results in competitions.
Mathematical Concepts Tested in 2006
The competition focused on evaluating participants’ understanding and application of a variety of mathematical concepts. These topics tested not only basic arithmetic skills but also the ability to think critically and apply advanced problem-solving strategies. By examining various branches of mathematics, the event encouraged participants to demonstrate their versatility and depth of knowledge in the subject.
Key Concepts Evaluated
Several core areas were emphasized throughout the competition. Participants were required to showcase proficiency in both elementary and more complex topics, allowing them to apply a wide range of skills to solve the problems presented.
- Number Theory: Problems related to divisibility, prime numbers, and properties of integers were a central focus.
- Geometry: Questions tested the ability to understand shapes, angles, symmetry, and spatial reasoning.
- Combinatorics: Participants were challenged with problems involving counting, arrangements, and basic probability concepts.
- Algebra: Equations, inequalities, and patterns were key components, testing both fundamental and advanced algebraic techniques.
- Logical Reasoning: Many questions required participants to apply deductive reasoning to arrive at correct solutions.
Application of Concepts in Problem Solving
Each question was designed to test participants’ ability to apply these mathematical concepts in novel and creative ways. This often meant that the solution required a combination of techniques rather than relying solely on one area of mathematics. As a result, the event not only assessed knowledge but also the ability to think critically and approach problems from multiple angles.
Sample Problems from 2006 Competition
This section presents a selection of problems from the 2006 competition, designed to give participants a sense of the types of questions they might encounter. These problems cover a broad range of topics and require both analytical thinking and creativity to solve. By reviewing these examples, you can gain insight into the difficulty level and structure of the questions, as well as the types of strategies that are most effective in solving them.
Problem 1: Number Theory
In this problem, participants were asked to determine the greatest common divisor of two given numbers and apply basic principles of number theory to find the solution.
- Problem Statement: What is the greatest common divisor of 48 and 180?
- Solution Approach: Use the Euclidean algorithm to find the greatest common divisor by dividing the larger number by the smaller one and repeating the process with the remainder until the remainder is zero.
- Answer: The greatest common divisor is 12.
Problem 2: Geometry
This problem required participants to use their understanding of basic geometry principles, including area, angles, and shapes, to solve a real-world problem.
- Problem Statement: A rectangle has a length of 12 cm and a width of 5 cm. What is the perimeter of the rectangle?
- Solution Approach: Apply the formula for the perimeter of a rectangle, which is P = 2 * (length + width), to calculate the perimeter.
- Answer: The perimeter is 34 cm.
These sample problems demonstrate the variety of topics tested and the different mathematical concepts participants need to be familiar with. Practicing with similar problems can help improve both accuracy and efficiency when solving questions under time constraints.
Answers to the First Set of Questions
This section provides the solutions to the first set of questions, which cover a range of topics designed to test various mathematical skills. By reviewing the solutions, participants can better understand the approach required to solve similar problems. The goal is to demonstrate the correct methodology, including necessary steps and explanations for each problem.
Problem 1: Basic Arithmetic
This problem tests the ability to perform basic operations with large numbers. The solution requires careful attention to detail in both the calculations and the order of operations.
- Problem Statement: Simplify the following expression: 256 + 72 × 3 – 144 ÷ 4.
- Solution Approach: Follow the order of operations (PEMDAS): first multiplication and division, then addition and subtraction. Begin by calculating 72 × 3 = 216, and 144 ÷ 4 = 36. Then, simplify: 256 + 216 – 36 = 436.
- Answer: The final result is 436.
Problem 2: Geometry and Perimeter
This problem focuses on geometry, specifically the calculation of perimeter in two-dimensional shapes. It emphasizes understanding of basic geometric properties.
- Problem Statement: A triangle has sides of lengths 5 cm, 8 cm, and 10 cm. What is the perimeter of the triangle?
- Solution Approach: The perimeter of a triangle is the sum of the lengths of its sides. Add the values: 5 + 8 + 10 = 23.
- Answer: The perimeter of the triangle is 23 cm.
By reviewing these solutions, participants can ensure they understand the correct approach to each type of problem. Practicing similar problems will help improve speed and accuracy for future sets of questions.
Solutions for Middle-Level Competition
This section provides detailed solutions to the middle-level problems, designed to challenge participants with a more advanced understanding of various mathematical concepts. These problems typically require not only basic knowledge but also the ability to think critically and apply multiple strategies to arrive at the correct solution. The solutions provided here demonstrate the process of tackling each problem step by step, ensuring clarity and understanding of the reasoning involved.
Problem 1: Advanced Number Operations

This problem tests the ability to handle more complex operations with numbers, requiring attention to both detail and the application of multiple steps to arrive at the correct result.
- Problem Statement: Solve the equation: 4x + 6 = 38.
- Solution Approach: Begin by subtracting 6 from both sides: 4x = 32. Then, divide both sides by 4: x = 8.
- Answer: The value of x is 8.
Problem 2: Geometry and Area Calculation
This question requires participants to apply knowledge of geometric figures and use the formula for the area of a shape.
- Problem Statement: Calculate the area of a rectangle with a length of 15 cm and a width of 7 cm.
- Solution Approach: The area of a rectangle is calculated using the formula: Area = length × width. Multiply 15 × 7 = 105.
- Answer: The area of the rectangle is 105 square centimeters.
By solving these problems, participants can reinforce their understanding of more advanced topics, and better prepare for similar challenges in future rounds. Practicing these types of questions will help strengthen problem-solving skills and build confidence in approaching complex problems.
Explaining Advanced Problems from 2006
This section dives into the more complex problems from the 2006 competition, offering detailed explanations for each solution. These problems often challenge participants to think critically and employ higher-level problem-solving techniques. We will break down each question step by step to ensure a clear understanding of the logic behind the solution, highlighting key strategies and concepts necessary for solving similar problems.
Problem 1: Algebraic Manipulations

This problem involves algebraic manipulation to solve an equation. The goal is to isolate the variable and solve for its value.
- Problem Statement: Solve for x: 5(x – 2) + 3 = 2x + 4.
- Solution Approach: Begin by distributing the 5 to both terms inside the parentheses: 5x – 10 + 3 = 2x + 4. Simplify the equation: 5x – 7 = 2x + 4. Now, subtract 2x from both sides: 3x – 7 = 4. Add 7 to both sides: 3x = 11. Finally, divide by 3: x = 11/3.
- Answer: The value of x is 11/3.
Problem 2: Logic and Pattern Recognition
This problem requires recognizing a pattern and applying logical reasoning to find the solution. It’s essential to observe trends and deduce the rule governing the sequence.
- Problem Statement: What is the next number in the sequence: 2, 5, 10, 17, __?
- Solution Approach: Notice the pattern in the differences between consecutive terms: 5 – 2 = 3, 10 – 5 = 5, 17 – 10 = 7. The differences are increasing by 2 each time. To find the next term, add 9 (the next difference) to 17: 17 + 9 = 26.
- Answer: The next number in the sequence is 26.
Understanding how to approach these advanced problems helps participants not only solve specific questions but also enhances their overall problem-solving strategies. By practicing similar problems, one can sharpen both analytical and logical reasoning skills, which are crucial for tackling challenging tasks in future competitions.
Analyzing Answer Patterns in Math Kangaroo
In this section, we will explore the answer patterns commonly found in various types of problems from the competition. Understanding these patterns is crucial for recognizing the structure of questions and the most efficient strategies to arrive at the correct solutions. By identifying recurring themes, participants can develop a deeper insight into problem-solving techniques and anticipate the types of challenges that may arise during the event.
Identifying Common Answer Choices
Many problems in the competition follow a predictable pattern in terms of the answer choices provided. Typically, there are several options, with one being correct and others serving as distractors. Analyzing these distractors can reveal key insights into the problem-solving process.
- Repetitive Numerical Sequences: Some problems present multiple answer choices that are part of a numerical sequence. Understanding the progression of the sequence can quickly lead to the correct choice.
- Elimination Strategy: Often, you can rule out one or two incorrect options immediately based on logical reasoning. This reduces the possible answers, making it easier to focus on the remaining choices.
Patterns in Complex Problem Types
Certain types of problems, such as those involving geometric shapes or algebraic expressions, exhibit their own set of answer patterns. Recognizing these trends can help participants quickly recognize how to manipulate the given information.
- Geometrical Problems: In many geometric problems, the solution involves basic properties of shapes like area, perimeter, or symmetry. Identifying the properties of the shapes can narrow down the possible solutions.
- Algebraic Problems: These problems often rely on solving equations or inequalities. Recognizing common forms of equations allows participants to quickly solve for the unknown variable.
By studying the answer patterns and understanding the logic behind the distractors, participants can improve their time management and accuracy during the competition. It helps to develop a systematic approach to recognizing and solving different types of questions, ultimately improving performance in the event.
Importance of Time Management During the Exam

Effective time management plays a crucial role in achieving success during any competitive exam. Being able to allocate the appropriate amount of time to each section ensures that participants can work efficiently through all the problems, without feeling rushed or leaving questions unanswered. With a limited amount of time to complete a set of diverse problems, a well-structured approach can greatly improve both accuracy and confidence.
During the exam, the balance between speed and accuracy is essential. Spending too much time on a single question can prevent you from answering others that may be easier or quicker to solve. On the other hand, rushing through questions may lead to careless mistakes. Understanding how to manage time effectively can help strike this balance, allowing for a thorough review of all questions without sacrificing quality.
Here are some key strategies to help manage time effectively:
- Set Time Limits: Allocate a specific amount of time for each section or question type, based on its difficulty level. This way, you can ensure that you stay on track without getting stuck on a single problem.
- Prioritize Simpler Problems: Begin by tackling the questions that you find easiest. This will give you a sense of accomplishment early on and leave more time for challenging problems later.
- Monitor the Clock: Regularly check the time to ensure that you are progressing at a steady pace. If you notice that you’re spending too long on a particular problem, move on and return to it later if needed.
By incorporating these strategies, you can maximize your performance during the exam, ensuring that you complete all questions and minimize the risk of missing out on easy points. Effective time management allows you to approach each question with a clear and focused mind, leading to better outcomes.
How to Improve Your Score in Future Contests
Improving your performance in competitive challenges requires a focused approach and consistent practice. By identifying areas of weakness and developing targeted strategies, you can enhance your problem-solving abilities and boost your overall score in future events. Achieving higher results isn’t solely about working harder, but also about working smarter.
One of the first steps to improvement is analyzing your past performances. Review your results from previous contests, paying special attention to the questions you found difficult or time-consuming. This will give you insight into which areas need more attention, whether it’s specific problem types, concepts, or time management issues.
Here are a few strategies to help you perform better in future competitions:
- Practice Regularly: Consistent practice is key to developing speed and accuracy. Work on solving a variety of problems to familiarize yourself with different question formats and difficulty levels.
- Focus on Weak Areas: Once you identify the topics you struggle with, dedicate more time to mastering them. Break down complex concepts into smaller, manageable parts and practice solving related problems.
- Take Timed Practice Tests: Simulating the exam environment with timed practice tests helps improve your ability to work under pressure. This also enables you to fine-tune your time management skills and avoid unnecessary stress.
- Review Mistakes: Analyze every mistake you make during practice and understand why the solution was wrong. This reflection helps prevent similar errors in the future and solidifies your understanding of the correct approach.
By applying these methods, you’ll gradually see improvement in your problem-solving techniques, time management, and confidence. With dedication and strategic preparation, you will be well-equipped to achieve higher scores in upcoming contests.
Benefits of Practicing Previous Math Kangaroo Tests
Practicing with past competition tests is one of the most effective strategies for improving performance. By revisiting previous challenges, participants can familiarize themselves with the format, question types, and level of difficulty, which significantly enhances preparation. Repetition not only strengthens problem-solving skills but also builds confidence, ensuring readiness for future contests.
Working through earlier tests provides several key advantages:
Familiarity with the Test Format
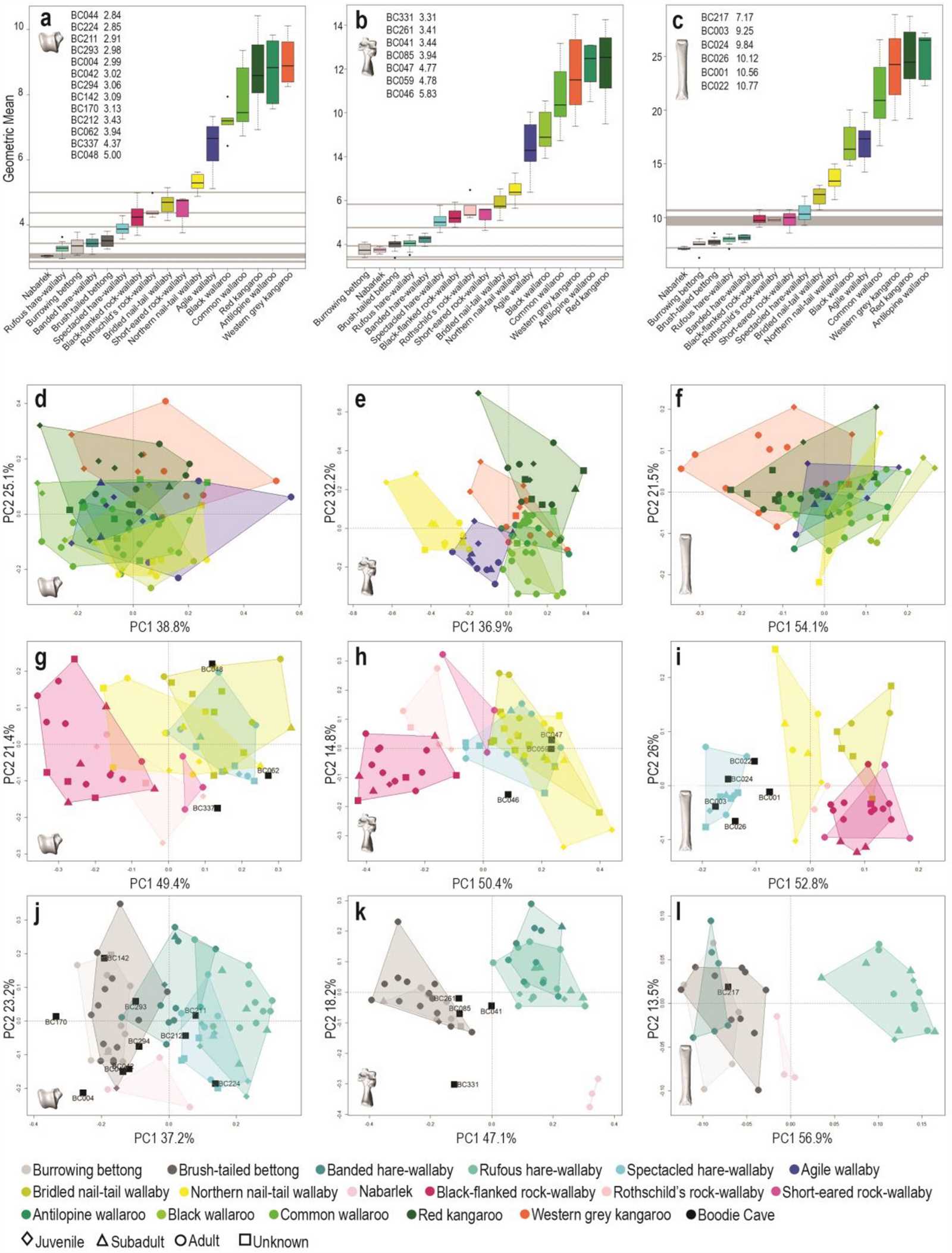
One of the main benefits is becoming accustomed to the structure of the event. By solving past problems, you can identify the patterns in question types and time constraints. This insight allows you to manage your time more effectively and know what to expect on the day of the competition.
Improved Problem-Solving Speed
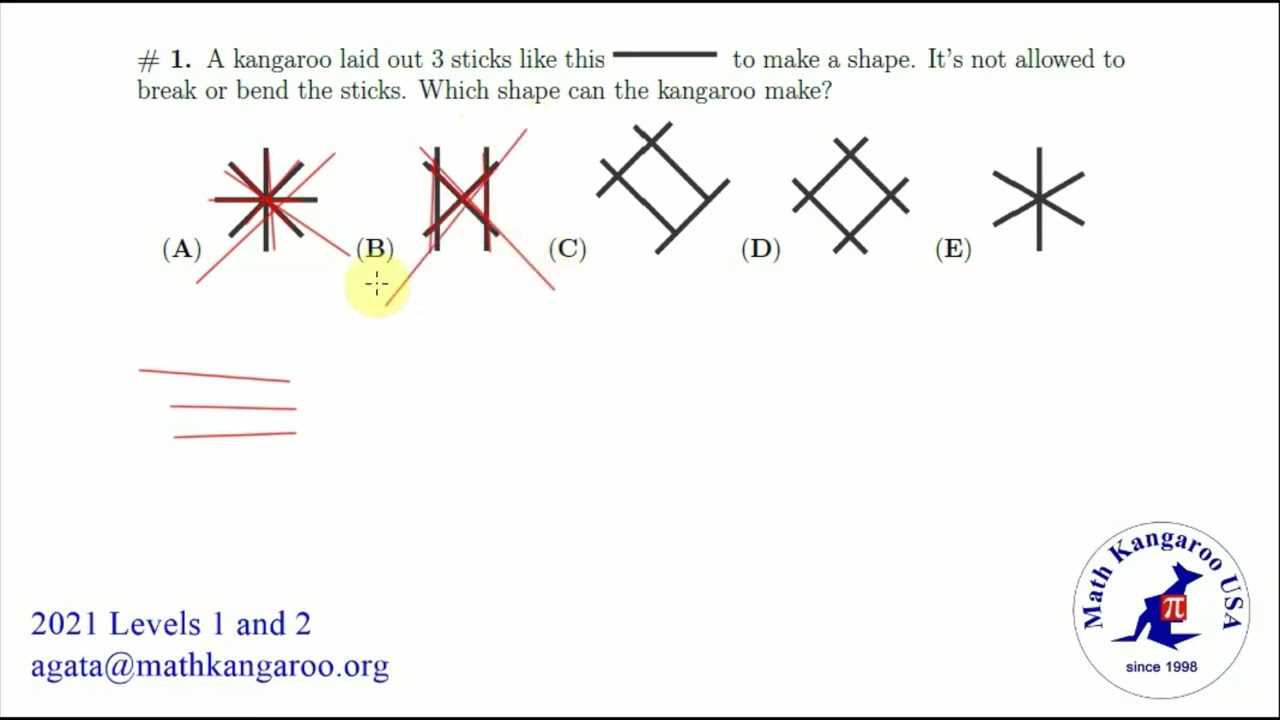
Regular practice helps you improve speed without sacrificing accuracy. As you solve more problems, you begin to recognize the quickest and most efficient ways to approach each question. This can be especially valuable in timed competitions where every second counts.
| Benefit | Description |
|---|---|
| Enhanced Critical Thinking | By tackling various types of problems, you sharpen your logical thinking and improve your ability to solve complex puzzles under pressure. |
| Increased Confidence | Success in solving past questions boosts confidence, making you more relaxed and focused during the actual contest. |
| Better Time Management | Knowing how much time to spend on each section and question helps you avoid spending too much time on difficult problems, leading to a more balanced approach. |
Incorporating past tests into your study routine is a smart way to ensure thorough preparation and improved results. Whether you’re focusing on specific problem types or aiming to get comfortable with the time limits, this practice is an essential part of any successful contest strategy.
Where to Find More Resources for Math Competitions
For participants aiming to deepen their understanding and preparation for future challenges, there is a wealth of materials available online and offline. These resources provide valuable practice, tips, and insights to help you succeed. Whether you are looking for problem sets, detailed solutions, or expert advice, there are many platforms and organizations offering specialized content for competitors at all levels.
Online Platforms and Websites

Numerous websites are dedicated to providing practice questions, solutions, and guides to help participants prepare for competitions. These platforms often feature archives of past exams, organized by difficulty, making it easy to find appropriate material for any skill level. Additionally, many offer interactive features such as forums and discussion groups where you can connect with other participants and share strategies.
- Official Competition Websites: The official website of the competition typically offers past exams and sometimes even interactive preparation tools. These sites may also provide updates on upcoming events and relevant news.
- Math Blogs and Forums: Community-driven websites and blogs often provide valuable insights and solutions to tricky problems. Many forums also host discussions about strategy, time management, and common challenges.
Books and Printed Materials
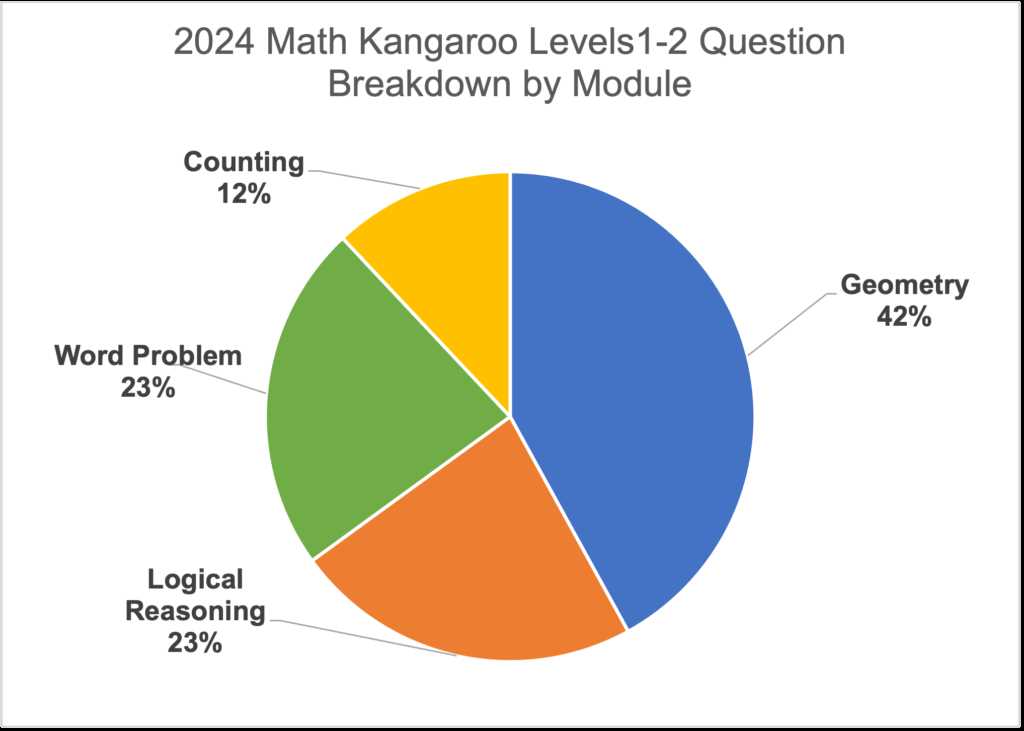
For those who prefer to study offline, there are many excellent books and guides available that focus on problem-solving techniques and tips for math-based competitions. These resources often include practice problems with solutions, as well as explanations of key concepts and strategies.
- Competition Prep Books: Many books are designed specifically for preparing for mathematical challenges. These books often break down problems into categories and provide step-by-step solutions for each one.
- Study Guides and Workbooks: Comprehensive workbooks offer a wide range of problems and solutions, allowing participants to hone their skills and track their progress.
In addition to these, many local educational centers, tutoring services, and universities offer workshops or study groups to help participants refine their skills. Exploring these resources can provide you with a well-rounded preparation approach, combining theoretical knowledge with practical experience.