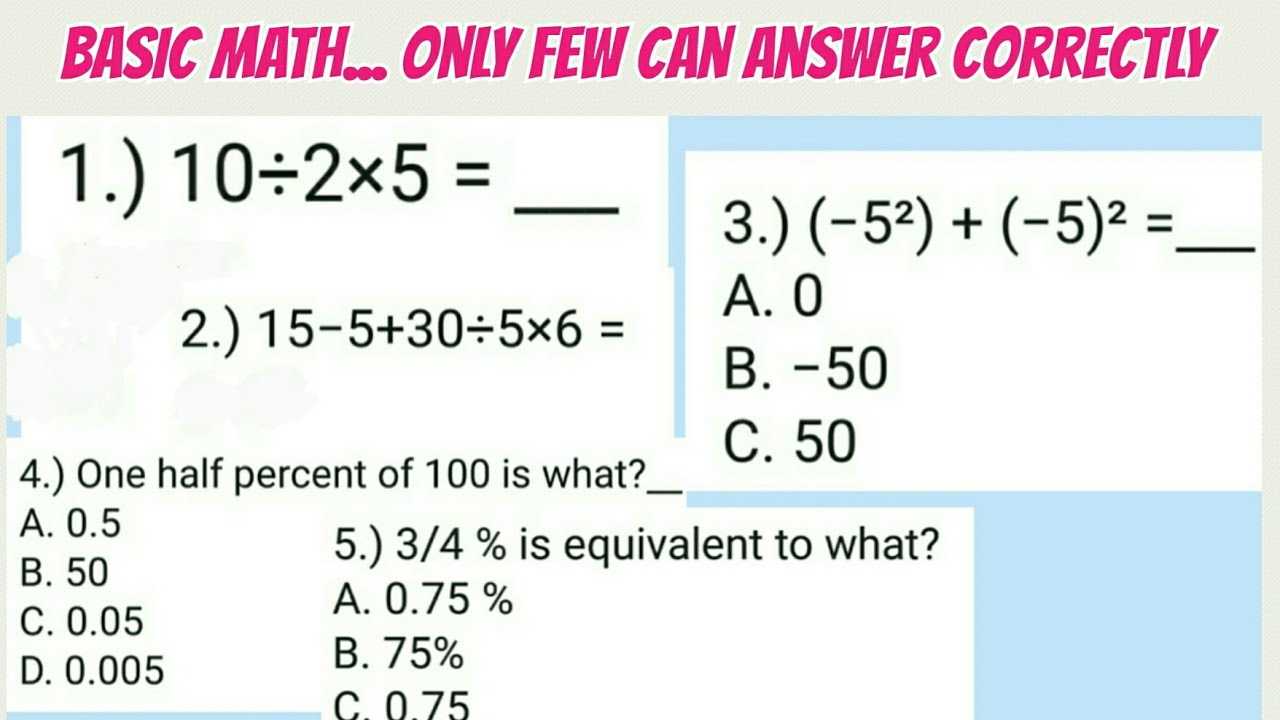
Preparing for an assessment in fundamental problem-solving can be challenging, but with the right approach, it becomes much more manageable. This guide is designed to help you navigate through key principles and strategies that will enhance your skills and boost your confidence. By mastering a few essential techniques, you can improve your performance and tackle any challenge effectively.
Practice and consistency are the cornerstones of mastering this subject. Regular engagement with sample problems and systematic review will sharpen your abilities and reduce the likelihood of errors. Focus on areas where you feel less confident and work through various problems to reinforce your understanding.
In this section, we’ll explore various methods to optimize your study time, such as breaking down complex problems into simpler steps and practicing under timed conditions. These practical tips will prepare you to face any challenge that comes your way, ensuring that you can approach every question logically and with ease.
Essential Test Preparation Techniques

When facing an assessment that challenges your problem-solving abilities, it’s crucial to approach it with a clear strategy. The key to success lies in understanding the underlying principles and being able to apply them efficiently. By focusing on structured practice and tackling a variety of sample problems, you can build the necessary skills to excel.
Breaking Down Complex Problems
One effective technique is breaking down difficult problems into smaller, manageable steps. This helps in identifying patterns and relationships between elements, making the overall task less daunting. By working through these steps methodically, you can arrive at the correct solution with greater confidence.
Enhancing Problem-Solving Speed
Another important aspect of preparation is improving your speed in solving questions. Practice under timed conditions will help you become more efficient and reduce the time spent on each problem. The more you familiarize yourself with various question types, the quicker you will be able to recognize the appropriate approach to solving them.
Understanding Key Concepts in Problem-Solving
To succeed in any assessment that challenges your problem-solving skills, it’s essential to have a solid understanding of the core principles. These foundational ideas form the building blocks for tackling a wide variety of challenges. Mastering these concepts ensures that you can approach any problem confidently and effectively.
Focus on the following areas to strengthen your understanding:
- Numerical operations: Master the basic operations like addition, subtraction, multiplication, and division, which are essential for solving many types of questions.
- Fractions and decimals: Understanding how to work with fractions, decimals, and their conversions is key to solving a wide range of problems.
- Algebraic expressions: Learn how to manipulate and solve equations, which is a vital skill in many advanced problems.
- Geometric shapes and properties: Familiarity with basic shapes, their properties, and formulas will help solve spatial reasoning problems.
Once you have a firm grasp on these concepts, practice applying them in different contexts to reinforce your understanding. This approach will help you become more adaptable when faced with unfamiliar questions.
How to Prepare for the Assessment
Effective preparation for any test involves more than just reviewing the material; it requires a structured plan that allows you to reinforce key concepts and identify areas that need improvement. A well-thought-out strategy helps you build confidence and ensures you’re fully ready to tackle the challenges that may arise during the assessment.
Below is a simple table outlining different strategies to help guide your study sessions:
| Preparation Strategy | Description | Recommended Time |
|---|---|---|
| Review Core Concepts | Revisit foundational topics and ensure you understand the basics well before diving into more complex material. | 1-2 hours per session |
| Practice Problem-Solving | Work through a variety of problems to apply concepts and improve your problem-solving skills. | 2-3 hours per session |
| Time Yourself | Practice under timed conditions to improve speed and efficiency in answering questions. | 30-45 minutes per practice session |
| Review Mistakes | Analyze errors made during practice to understand where you went wrong and prevent similar mistakes. | 30 minutes per session |
By following this structured approach, you’ll be able to prepare systematically, enhancing both your knowledge and your ability to perform under pressure.
Essential Formulas to Remember
Understanding key formulas is crucial when preparing for any assessment involving numerical problem-solving. These essential equations serve as tools to simplify complex tasks, allowing you to quickly and accurately find solutions. Whether you are working with shapes, equations, or data sets, knowing these formulas is the first step towards mastering any challenge.
Arithmetic and Algebraic Formulas
In many cases, basic arithmetic and algebraic formulas form the foundation for solving more advanced problems. Some of the most commonly used formulas include:
- Area of a rectangle: Length × Width
- Circumference of a circle: 2π × Radius
- Quadratic equation: x = (-b ± √(b² – 4ac)) / 2a
- Sum of an arithmetic series: S = n/2 × (a₁ + aₙ)
Geometric and Statistical Formulas
For geometry and statistics, there are specific formulas that are indispensable for accurate calculations:
- Area of a triangle: 1/2 × Base × Height
- Pythagorean theorem: a² + b² = c² (for right-angled triangles)
- Mean of a data set: (Sum of all values) / Number of values
- Standard deviation: √(Σ(xᵢ – μ)² / N)
Mastering these formulas will give you the confidence to approach problems methodically and accurately, ensuring success on test day.
Strategies for Solving Problems
Effective problem-solving requires more than just applying formulas; it involves strategic thinking and a clear method to tackle challenges. By using a structured approach, you can break down complex problems into manageable steps, improving both your accuracy and efficiency. These strategies are designed to help you approach each question confidently and systematically.
Here are some key strategies to consider:
- Understand the problem: Carefully read the question and make sure you fully understand what is being asked. Identify key information and highlight any important details.
- Break the problem into smaller steps: Instead of attempting to solve the entire problem at once, break it down into smaller, more manageable parts. Tackle each step one at a time.
- Use estimation: In some cases, estimating the answer can help you narrow down possible solutions and avoid wasting time on calculations that might not be necessary.
- Check your work: After solving, review your solution carefully to ensure no mistakes were made. This step is crucial for verifying accuracy.
By practicing these strategies regularly, you will build a problem-solving approach that helps you remain calm and focused, ensuring better results under pressure.
Common Mistakes to Avoid in Problem-Solving
Even the most prepared individuals can make errors when solving complex problems. These mistakes often arise from simple misunderstandings or rushed calculations. By identifying and addressing common pitfalls, you can improve your accuracy and avoid losing valuable points during an assessment.
Here are some typical mistakes to watch out for:
| Mistake | Description | How to Avoid |
|---|---|---|
| Misreading the Question | Overlooking key details or misunderstanding what the question is asking. | Read the problem carefully and highlight important information. |
| Skipping Steps | Jumping to conclusions without fully working through each part. | Break down the problem into smaller steps and solve systematically. |
| Incorrect Calculations | Making simple errors in arithmetic or applying wrong operations. | Double-check calculations and verify results using a different method. |
| Not Checking the Final Answer | Rushing through the final solution without verifying accuracy. | Always review your work before submitting to ensure everything is correct. |
By being mindful of these common errors and taking the time to avoid them, you’ll increase your chances of success and approach each problem with more confidence and precision.
Time Management Tips for the Assessment
Efficiently managing your time during any assessment is crucial for completing all tasks accurately and without unnecessary stress. Proper time allocation ensures that you have enough time to solve each question thoroughly while avoiding rushing through any of them. By following a strategic approach, you can make the most of your available time and perform at your best.
Pre-Assessment Preparation
Before the test, it’s important to plan ahead so that you are familiar with the format and know how much time to allocate to each section. Setting realistic time limits for each part can help prevent wasting time on more difficult questions.
| Task | Time Allocation | Tip |
|---|---|---|
| Read through all questions | 5-10 minutes | Quickly scan the questions to identify the easiest and hardest ones. |
| Work on simple questions | 40-50 minutes | Answer the easier questions first to save time for tougher ones. |
| Review answers | 10-15 minutes | Use the remaining time to check for mistakes and verify your solutions. |
During the Test
Once you start, it’s important to stick to your time limits. If you get stuck on a problem, don’t dwell on it for too long. Move on to another question and return later if time permits.
By applying these time management strategies, you’ll be able to approach each question calmly and with a clear focus, ensuring that you complete the assessment successfully within the allotted time.
How to Improve Calculation Speed
Being able to perform calculations quickly and accurately is a valuable skill, especially when facing time-sensitive assessments. Improving your calculation speed not only boosts your efficiency but also enhances your ability to focus on more complex problems. With consistent practice and the right techniques, you can become faster and more confident in solving numerical tasks.
Here are some effective ways to speed up your calculations:
- Practice Mental Arithmetic: Regularly practice doing simple calculations in your head. This helps you eliminate reliance on calculators and strengthens your ability to quickly compute results.
- Memorize Key Facts: Memorize multiplication tables, squares, and common fractions. Knowing these by heart will allow you to perform operations quickly without having to pause and calculate.
- Use Shortcuts: Learn shortcuts for common operations, like multiplying by powers of 10 or dividing by simple fractions. This reduces the time spent on more repetitive tasks.
- Break Down Complex Problems: Instead of tackling a difficult calculation all at once, break it down into smaller, easier steps. This makes solving more manageable and faster.
- Set Time Limits: Challenge yourself by setting a time limit for solving problems. This will help you work under pressure and improve your ability to complete calculations swiftly.
By regularly practicing these techniques, you’ll notice a significant improvement in your ability to perform calculations more efficiently, allowing you to save valuable time when solving complex problems.
Practical Examples of Problem Solving
Understanding how to approach and solve problems is essential for developing strong problem-solving skills. Working through examples helps you apply theoretical knowledge to real-world scenarios, making it easier to tackle a variety of challenges. Here, we’ll walk through some practical examples of problems you might encounter, along with step-by-step solutions to guide you.
Here are a few examples of common problems, demonstrating different techniques and approaches:
- Example 1: Area of a Triangle
Problem: Calculate the area of a triangle with a base of 6 cm and a height of 8 cm.
Solution: Area = 1/2 × base × height = 1/2 × 6 × 8 = 24 cm².
- Example 2: Solving a Linear Equation
Problem: Solve for x in the equation 3x + 4 = 19.
Solution: Subtract 4 from both sides: 3x = 15. Then divide both sides by 3: x = 5.
- Example 3: Volume of a Cylinder
Problem: Find the volume of a cylinder with a radius of 4 cm and a height of 10 cm.
Solution: Volume = π × r² × h = 3.14 × 4² × 10 = 502.4 cm³.
- Example 4: Percentage Increase
Problem: A shirt originally costs $50. If the price increases by 20%, what is the new price?
Solution: Increase = 50 × 0.20 = 10. New price = 50 + 10 = $60.
These examples illustrate a variety of techniques for solving different types of problems. By practicing similar problems, you’ll develop a deeper understanding and improve your ability to solve any challenge quickly and accurately.
Tips for Reviewing Essential Topics
Reviewing fundamental concepts is key to reinforcing your knowledge and boosting your confidence before an assessment. A focused approach to revisiting key areas will help you identify any gaps in your understanding and ensure that you are well-prepared. Below are some effective strategies to review essential topics efficiently.
Active Practice and Application

Simply reading through notes may not be enough to fully grasp important concepts. Active practice involves solving problems, applying formulas, and working through examples. This hands-on approach helps you better internalize the material and improve your problem-solving skills.
- Work on Sample Problems: Solve a variety of problems to test your understanding of each concept. This will help reinforce your knowledge and identify areas where you need more practice.
- Use Flashcards: Create flashcards for formulas, key concepts, and important procedures. Review them regularly to keep the information fresh in your mind.
- Practice Under Time Constraints: Time yourself while solving problems to simulate test conditions. This will help you improve your speed and accuracy under pressure.
Focus on Weak Areas
While it’s important to review all topics, it’s especially helpful to focus on areas where you feel less confident. Spend more time working through problems related to these topics, and don’t hesitate to seek additional help if needed.
- Review Mistakes: Go over any mistakes you’ve made in previous practice sessions. Understanding where you went wrong will help you avoid repeating those errors.
- Break Down Complex Topics: If you find certain topics challenging, break them down into smaller, more manageable sections. Take one step at a time to make them easier to understand.
By incorporating these strategies into your review process, you’ll strengthen your grasp of key topics and approach your assessment with greater confidence and preparedness.
Why Practice Makes Perfect in Math
Repetition is a powerful tool for mastering any skill, and solving numerical problems is no exception. When it comes to overcoming challenges in this area, consistent practice not only sharpens your abilities but also builds confidence. By continually applying what you’ve learned, you strengthen your understanding and develop a more intuitive grasp of concepts.
Here are some reasons why regular practice is essential for improvement:
- Enhances Problem-Solving Skills: The more problems you solve, the more you refine your approach and become faster at recognizing patterns. This leads to quicker and more accurate solutions over time.
- Increases Familiarity with Concepts: Repeated exposure to different types of problems helps you internalize concepts and formulas, making it easier to recall and apply them when needed.
- Builds Confidence: As you practice regularly, you become more comfortable with tackling even the most difficult problems. This confidence can help reduce anxiety and improve your performance.
- Identifies Weak Areas: Regular practice helps reveal areas where you may struggle, allowing you to target these weaknesses and focus on improving them before moving on to more advanced topics.
Ultimately, practice allows you to solidify your knowledge, improve efficiency, and develop the skills necessary to solve problems accurately and with confidence. The more time you dedicate to practicing, the better equipped you’ll be to handle challenges in the future.
Using Online Resources for Study
In today’s digital age, the internet offers a wealth of tools and resources that can significantly enhance your learning experience. From interactive tutorials to problem-solving guides, online platforms provide convenient access to materials that can help reinforce your understanding and improve your skills. Utilizing these resources effectively can be a game-changer for anyone looking to succeed in their studies.
Here are some types of online resources that can support your learning:
- Interactive Practice Websites: Many websites offer interactive problems and instant feedback. These sites often cater to different skill levels, helping you gradually build your abilities and track progress.
- Video Tutorials: Platforms like YouTube or educational sites feature videos that break down complex topics into easy-to-understand lessons. Visual aids and step-by-step instructions can make challenging concepts clearer.
- Online Courses: Enrolling in an online course can provide structured learning. These courses often include detailed lectures, quizzes, and assignments designed to reinforce your knowledge and test your understanding.
- Discussion Forums: Engaging in online forums allows you to ask questions, share ideas, and learn from others. Sometimes, discussing a problem with peers or experts can offer valuable insights you might not have considered.
- Apps and Tools: There are a variety of apps available for practicing calculations, visualizing problems, and even solving equations. These tools can be used on-the-go and provide real-time feedback.
By incorporating these online resources into your study routine, you can enhance your learning, practice more efficiently, and gain access to a variety of perspectives and techniques. The more resources you tap into, the more equipped you’ll be to tackle even the most challenging topics.
What to Do Before the Exam Day
Preparing for a test goes beyond just reviewing content. It’s about setting yourself up for success in the final moments leading up to the event. The day before the test is critical for consolidating your knowledge, managing stress, and ensuring you’re physically and mentally prepared. Proper preparation can make a significant difference in your performance, so it’s essential to focus on the right steps.
Here are some key actions to take before the big day:
- Review Key Concepts: Make sure to go over the most important topics and any areas where you feel less confident. Focus on understanding core principles rather than trying to memorize everything.
- Practice Problems: Do a few practice questions to reinforce your problem-solving abilities. This helps build confidence and ensures you’re comfortable with the types of problems that might appear.
- Get Organized: Ensure you have everything you’ll need for the test day, such as necessary materials (pens, calculators, ID), and know the exact time and location of the test.
- Get Plenty of Rest: A good night’s sleep is crucial for cognitive function. Avoid cramming or staying up too late, as this can negatively affect your focus and recall.
- Eat Well: A balanced meal before the test can help maintain energy levels and focus. Avoid heavy, greasy foods that could make you feel sluggish.
- Stay Calm: Manage your stress by doing something relaxing, such as taking a walk, meditating, or listening to music. Keeping a positive mindset is essential for staying focused during the test.
By preparing wisely, you set the stage for a successful test. Taking the time to review, rest, and organize ensures you’re not only ready intellectually but also physically and mentally equipped to perform your best.
How to Stay Calm During the Test
It’s common to feel nervous before and during a challenging assessment, but maintaining composure is key to performing well. Stress can cloud your judgment and hinder your ability to recall important information. By using strategies to stay calm, you can approach the test with confidence and clarity. Here are some effective techniques to help you keep your cool throughout the process.
Breathing Techniques
When anxiety strikes, it’s important to focus on your breath. Deep breathing helps activate your body’s relaxation response and can quickly lower stress levels. Try breathing in deeply for a count of four, holding for four, and exhaling slowly for four. Repeat this for a few minutes to calm your nerves and reset your focus.
Focus on the Present
Worrying about the questions you haven’t reached yet or stressing over the time limit can make things worse. Instead, concentrate on one problem at a time. Focus on the task in front of you and tackle it methodically. If you find yourself getting overwhelmed, take a moment to pause, breathe, and return your attention to the current question.
Positive Visualization is another powerful tool. Before the test, imagine yourself answering questions confidently and successfully. This can help reinforce a positive mindset, reducing anxiety when you’re in the actual situation.
Stay Hydrated and take breaks when possible. A clear, hydrated mind will allow you to think better and make more accurate decisions. Don’t hesitate to take a short break if you start feeling overwhelmed during the test.
By staying calm and employing these strategies, you’ll be able to maintain a level head and perform to the best of your ability during the entire assessment.
Answering Multiple-Choice Questions Efficiently

Multiple-choice questions can be tricky, but with the right strategies, you can answer them more quickly and accurately. Instead of feeling overwhelmed by the variety of options, it’s essential to approach these questions methodically. By following a few simple techniques, you can enhance your efficiency and increase your chances of selecting the correct answer.
Read Carefully and Understand the Question
Before jumping to the options, make sure to read the question thoroughly. Understand exactly what is being asked and identify any keywords or phrases that give you clues about the answer. This will prevent you from choosing the wrong option due to misinterpreting the question.
Eliminate Clearly Incorrect Options
One of the best strategies is to rule out options that are obviously incorrect. Even if you’re unsure about the correct answer, eliminating one or two wrong answers increases your odds of choosing the right one. This strategy is particularly helpful when you’re left with two plausible options.
- Look for extreme words like “always” or “never” in the answer choices, as they are often signs of incorrect answers.
- If you notice that an option is too detailed or off-topic, it’s likely not the correct one.
Use Logic and Context Clues
Sometimes, your best tool is common sense. If you’re stuck, try to think logically about the question and its possible answers. Use context from the rest of the test to help guide your decision. For instance, if one answer seems to align with other information you’ve already learned, it might be the best choice.
Don’t Overthink It

If you’re down to two options, trust your instincts. Often, your first choice is the correct one. Avoid second-guessing yourself, as this can lead to unnecessary mistakes. If you’re running out of time, it’s better to choose an answer based on the process of elimination than to leave it blank.
- If time is running short, try not to spend too long on any single question.
- If necessary, mark questions that you’re unsure about and come back to them later.
By using these strategies, you can work through multiple-choice questions more effectively and confidently. The key is to stay calm, think logically, and trust your preparation.
How to Handle Word Problems in Math
Word problems can often seem intimidating, but breaking them down into smaller, manageable steps can make them much easier to tackle. Instead of being overwhelmed by the length or complexity of the problem, focus on understanding what is being asked and how you can apply the right techniques to solve it. With a clear plan, word problems become less of a challenge.
Read the Problem Carefully
The first step is always to read the problem carefully, multiple times if necessary. Pay close attention to the key details and identify the numbers, variables, and relationships between them. Look for keywords like “total,” “difference,” or “ratio,” which can provide clues as to what mathematical operation is required. Understanding the context is crucial before jumping into solving.
Translate Words into Mathematical Expressions
Once you’ve understood the problem, translate the information into a mathematical equation or expression. Many word problems describe real-world situations that can be represented by numbers and operations. For example, if a problem mentions a total of items or a difference in values, you can convert these descriptions into addition, subtraction, multiplication, or division operations.
- Look for phrases that indicate operations, such as “increased by” (addition), “less than” (subtraction), or “times” (multiplication).
- If the problem involves a rate or a ratio, make sure to set it up as a fraction or equation representing that relationship.
Double-Check Your Answer
Once you’ve solved the problem, take a moment to review your solution. Check if the answer makes sense in the context of the problem. If the answer seems unreasonable, revisit your steps and ensure that you haven’t missed anything important. Word problems often require a little extra care to make sure you’re answering the right question with the right method.
By following these steps, you can make tackling word problems much more manageable. Practice these strategies, and you’ll find that these types of problems become less intimidating over time.
Revising Solutions After the Test
After completing any assessment, it’s crucial to take time to review your responses and reflect on the process. Revising solutions helps to identify areas for improvement and reinforces the understanding of concepts that may have been unclear. This step can turn mistakes into learning opportunities, strengthening your problem-solving skills for the future.
Analyze Mistakes and Misunderstandings
Start by carefully reviewing each problem you found challenging or answered incorrectly. Identify the specific errors made–whether they were calculation mistakes, misinterpretation of the question, or choosing the wrong approach. Understanding the root cause of each mistake will prevent you from repeating it next time.
- Did you misread the question or overlook important details?
- Were the steps in your calculations followed correctly, or was there a mistake in the process?
Review the Correct Solutions and Techniques
After analyzing your errors, go through the correct solutions step by step. Compare the correct approach with yours and note any differences. This process not only helps you understand the correct method but also teaches you alternative strategies for solving similar problems in the future. The goal is to solidify the correct techniques and integrate them into your problem-solving habits.
By thoroughly revisiting your work, you gain valuable insights into your strengths and weaknesses, which allows you to continuously improve your skills and better prepare for future challenges.
What to Do if You Miss a Question
Missing a question during any test can be discouraging, but it’s important to handle the situation calmly and constructively. The key is not to dwell on the mistake, but to understand it and learn from it. By approaching missed questions as opportunities for growth, you can enhance your skills and ensure better results next time.
Stay Calm and Focused
It’s natural to feel frustrated if you miss a question, but it’s essential to stay composed. Panicking or stressing over the mistake will only cloud your judgment and affect your performance on the rest of the test. Take a deep breath and focus on the next tasks. Remember that one missed question does not define your overall ability.
Review the Missed Question
After the test, review the question you missed carefully. Determine whether it was due to a simple mistake, a misunderstanding of the problem, or a lack of knowledge on the topic. Ask yourself if there was a different way you could have approached the question. This self-reflection is crucial for improving your problem-solving skills.
- Was the mistake due to a misinterpretation of the question?
- Did you overlook a key detail or step in the solution process?
- Could a different strategy or formula have helped you find the correct answer?
By reviewing your errors and addressing them, you can build a stronger foundation for future challenges and avoid making the same mistakes again. The process of learning from your mistakes is an essential part of growth and improvement.