Conceptual Physics Chapter 9 Workbook Answers

The material covered in this section presents fundamental principles that are essential for grasping the core ideas of this subject. By working through the exercises, students can strengthen their understanding and apply theoretical concepts to practical situations. The focus is on clarity and ensuring a deep comprehension of the various processes at play.

Throughout the section, you will encounter a range of challenges designed to test your ability to think critically and solve complex problems. The goal is to break down each topic into manageable parts, providing you with the tools needed to tackle more advanced material with confidence. Whether you’re revisiting a concept or encountering it for the first time, this section offers valuable insights and structured guidance.

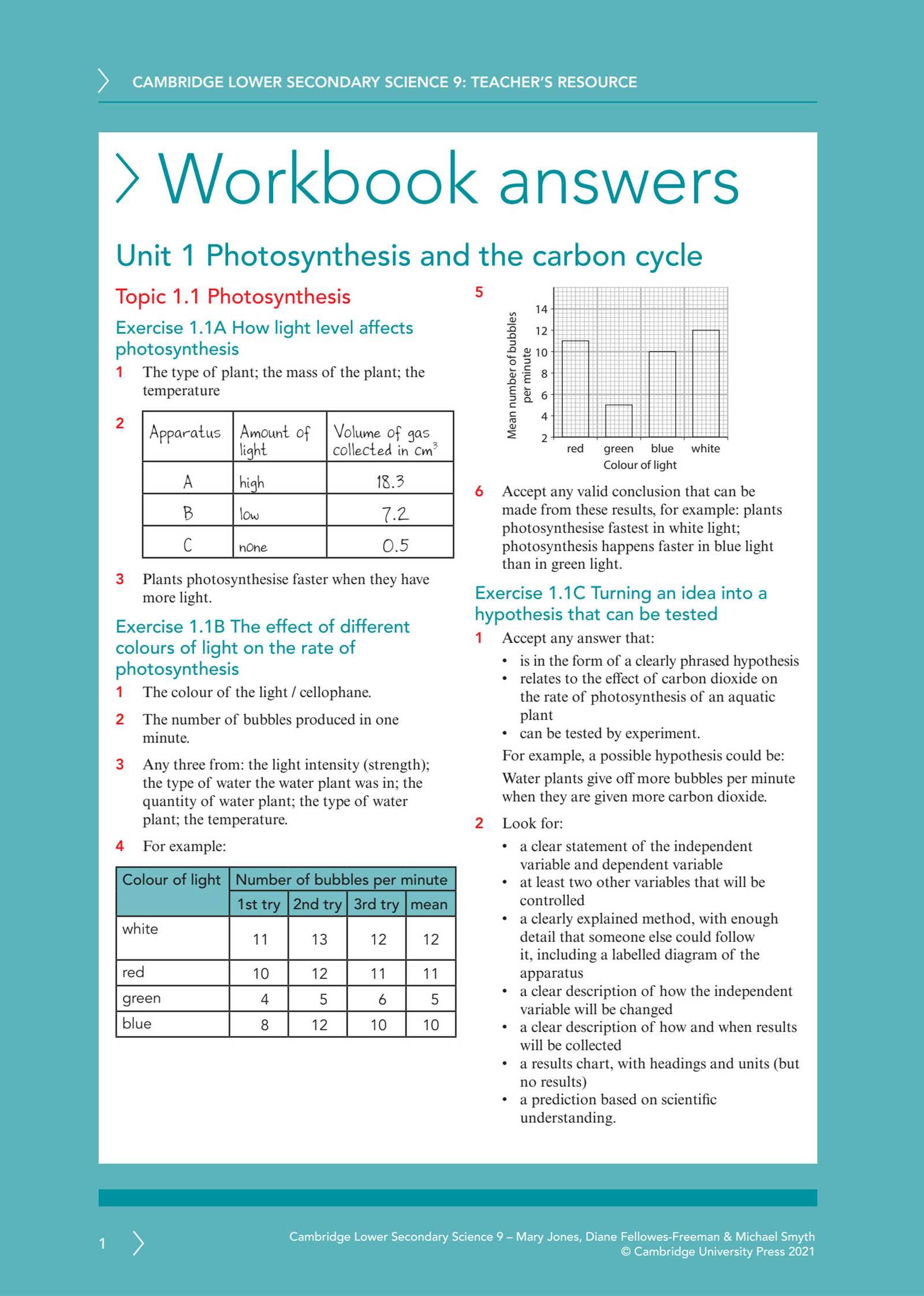
Conceptual Physics Chapter 9 Workbook Answers

This section provides detailed solutions and explanations to key exercises found in the ninth segment of the material. The primary goal is to help learners better understand the concepts presented, offering clear steps to resolve common questions. These solutions are designed to enhance comprehension and guide students through complex problem-solving processes.

Each example has been broken down into easy-to-follow steps, allowing learners to see how to approach similar challenges on their own. By understanding the logic behind each solution, you will gain a deeper appreciation for the underlying principles and improve your overall grasp of the subject.

Working through these explanations not only reinforces your ability to tackle problems but also strengthens critical thinking skills essential for progressing in the subject. This section is a valuable resource for mastering important concepts and preparing for future assessments.

Key Topics in Chapter 9

This section introduces the fundamental concepts that form the core of the ninth unit in the course. It covers a variety of crucial ideas that are essential for building a solid foundation in the subject. By exploring these topics in detail, students will gain a comprehensive understanding of the principles that guide the material and its applications.

Main Concepts Covered

The key areas of focus in this part include the relationships between different variables, how to interpret data effectively, and methods to solve complex problems. These topics are designed to challenge learners while reinforcing core skills that will be valuable in more advanced studies.

Application of Core Ideas

Understanding the key topics in this section not only helps students grasp the theoretical aspects but also enables them to apply these concepts to real-world scenarios. The exercises provided in this section are aimed at enhancing both theoretical understanding and practical problem-solving ability.

Topic	Description	Application
Core Principles	Fundamental concepts essential for further learning	Real-world problem-solving techniques
Data Interpretation	Understanding how to analyze and interpret numerical data	Effective decision-making in practical situations
Problem Solving	Step-by-step approaches to resolving complex problems	Application to future coursework and real-life challenges

Understanding Physics Concepts in Detail

This section delves deeply into the essential principles that form the backbone of the subject. By examining each idea in depth, students can gain a clearer understanding of how the various concepts interconnect and influence one another. This detailed exploration ensures that learners grasp not only the surface-level information but also the underlying mechanisms at play.

The goal here is to break down complex topics into more manageable parts, highlighting key relationships and patterns that are crucial for solving problems. Through careful analysis, the material provides a solid foundation for tackling both theoretical questions and practical applications.

Focusing on these details helps to build a more comprehensive understanding, which is critical for progressing in more advanced studies and applying knowledge in real-world contexts. Each concept is examined from different angles, ensuring a well-rounded approach to mastering the subject.

Step-by-Step Solutions for Exercises

This section provides detailed, methodical explanations for solving the exercises in the course material. Each problem is broken down into clear, manageable steps that guide you through the process from start to finish. By following these instructions, you will be able to see how each solution is derived and understand the logical progression behind it.

Through this structured approach, learners can develop a deeper comprehension of the problem-solving techniques that are essential for mastering the subject. Each step is carefully explained to highlight the reasoning behind every action, ensuring that you grasp not only the solution but also the principles that lead to it.

These solutions serve as a valuable resource for reinforcing key concepts while providing practical examples of how to apply them effectively. By practicing with these step-by-step guides, students can build confidence in their ability to tackle similar challenges independently.

Clarifying Difficult Problems

This section focuses on addressing some of the more challenging issues that learners often encounter in the course material. By breaking down complex problems into simpler components, it becomes easier to understand and solve them. The aim is to provide clear explanations that shed light on difficult concepts, making them more accessible and less intimidating.

Each problem is analyzed in depth to identify common obstacles and misconceptions. Step-by-step guidance is provided to help clarify the process and demonstrate the most effective strategies for tackling these challenges. This approach allows students to not only find solutions but also gain insight into the reasoning behind each step.

By working through these explanations, learners can improve their ability to approach complex problems with confidence. This section offers practical insights that will be valuable in both academic settings and real-world applications, ensuring a solid understanding of the material.

Breaking Down Chapter 9 Examples

This section focuses on analyzing key examples from the material to help you understand how different concepts are applied in problem-solving. By dissecting each example step by step, you can see how various techniques and principles are used to reach the final solution. The goal is to provide a clearer understanding of the methods and thought processes involved.

Key Steps in Each Example

Each example is broken down into manageable parts to show how to approach the problem logically. By following this structure, you will learn how to identify key components and apply the correct methods. Here’s what you can expect from each example:

• Identification of important variables
• Step-by-step breakdown of the solution
• Clear explanation of the reasoning behind each step
• Tips for recognizing common patterns and strategies

Practical Applications of Each Example

The examples are not only designed to explain the material but also to demonstrate how these principles can be used in real-world situations. Understanding these applications enhances your ability to tackle similar problems in the future.

1. Use in laboratory settings
2. Real-life problem-solving scenarios
3. Application to advanced coursework

Important Formulas from Chapter 9

This section highlights the key equations that are crucial for solving problems in the current unit. Understanding these formulas is essential, as they provide the foundation for applying theoretical knowledge to practical situations. By mastering these expressions, learners can gain a deeper understanding of the relationships between different variables.

Key Equations to Remember

The following formulas play a significant role in solving various problems within the section. It is important to not only memorize them but also to understand when and how to apply them effectively:

• Equation 1: Describes the relationship between force and motion.
• Equation 2: Relates energy and work in a system.
• Equation 3: Provides a method for calculating velocity in dynamic situations.
• Equation 4: Connects mass and acceleration with resulting force.

Applications of Key Formulas

Once you are familiar with these formulas, it’s important to understand how to apply them in different contexts. The following examples illustrate practical uses:

1. Determining the work done when a force acts over a distance.
2. Calculating the speed of an object in motion using known variables.
3. Applying the principle of conservation of energy in closed systems.

Common Mistakes in Problems

While solving problems in this field, learners often encounter a variety of challenges that can lead to errors. These mistakes typically stem from misunderstandings of key concepts, incorrect application of formulas, or simple calculation oversights. Recognizing these common pitfalls is essential to improving problem-solving skills and avoiding repeated errors.

By identifying frequent mistakes, students can develop strategies to address and correct them, leading to better results and a deeper understanding of the material. Here are some of the most common errors made during exercises:

Frequent Errors to Avoid

• Forgetting units: Failing to include or convert units properly can lead to incorrect results.
• Incorrect formula application: Using the wrong equation for a specific problem often results in misleading outcomes.
• Sign errors: Neglecting the direction of forces or velocities can lead to mistakes in vector-based calculations.
• Rounding too early: Rounding numbers prematurely can lead to inaccurate final answers.
• Assuming relationships are linear: Many variables have non-linear relationships, and applying linear assumptions can result in errors.

How to Avoid These Mistakes

To minimize errors and improve accuracy, keep the following tips in mind:

1. Double-check that you are using the correct formula and units for each problem.
2. Carefully work through each step of the solution to catch sign errors or miscalculations.
3. Avoid rounding off numbers until the final step to preserve precision.
4. Review the problem to ensure that you are not making incorrect assumptions about relationships between variables.

Study Strategies for Success

Achieving success in this subject requires more than just reading through the material–it involves adopting effective techniques that foster a deeper understanding. To truly master the concepts, it is essential to engage with the content in a way that encourages critical thinking, application, and consistent practice. By employing the right strategies, you can significantly improve both your comprehension and problem-solving skills.

Effective Approaches to Learning

To maximize your study time and enhance retention, consider using the following strategies:

• Active Learning: Engage actively with the material by solving problems, explaining concepts to others, or teaching yourself through practice exercises.
• Use of Visual Aids: Diagrams, charts, and concept maps can help you better visualize complex relationships between variables and concepts.
• Practice Regularly: Repetition is key to reinforcing understanding. Regular practice with varied problems solidifies your knowledge and helps identify areas for improvement.
• Group Study: Collaborating with peers can provide different perspectives and insights that might help clarify difficult topics.

Maximizing Your Study Sessions

In addition to adopting effective techniques, structuring your study sessions can improve focus and retention:

1. Break Sessions Into Segments: Study in shorter, focused intervals to avoid burnout and increase concentration.
2. Review Regularly: Consistent review of previous material ensures that key concepts remain fresh in your mind.
3. Prioritize Weak Areas: Focus more time on topics or problems that are challenging, while still maintaining your strengths.

How to Use the Workbook Effectively

To get the most out of the exercises provided, it’s important to approach them with a structured method. Simply reading through the questions isn’t enough–active participation and thoughtful engagement with the material are essential. By using the resources in a strategic way, you can strengthen your understanding, clarify concepts, and improve problem-solving skills.

Step-by-Step Approach

Here are some key steps for using the exercises effectively:

• Read Instructions Carefully: Before diving into the questions, make sure to fully understand the task and what is being asked. This ensures you apply the right approach from the start.
• Work Through Problems Systematically: Break down each question into smaller, manageable parts. Solve each section step-by-step, and double-check your work to avoid simple mistakes.
• Use Examples as Guides: Review example problems for patterns in the solution process. These can serve as models for approaching similar questions.

Maximizing Retention

To enhance retention and understanding, consider these additional strategies:

• Write Out Solutions: Writing out each step in your solution helps reinforce the thought process behind the answer.
• Review Completed Exercises: After completing the problems, revisit them periodically to ensure concepts are solidified in your memory.
• Test Yourself: Regular self-testing with new variations of problems strengthens your knowledge and helps identify weak areas that need further practice.

Understanding Key Terminology in Science

In any scientific field, understanding the essential terminology is crucial for grasping the concepts and principles. The correct use of terms allows for clearer communication and a deeper understanding of complex ideas. Whether you’re dealing with forces, energy, or motion, each term plays a specific role in explaining natural phenomena. Mastering these key terms is the first step in developing a strong foundation in the subject.

Familiarizing yourself with the most important terms is vital for effectively solving problems and applying theoretical concepts in practical situations. Here’s a breakdown of some of the fundamental terms you are likely to encounter:

Term	Definition
Force	A push or pull on an object, typically measured in newtons.
Energy	The capacity to do work, often classified as potential or kinetic.
Velocity	The rate at which an object changes its position in a given direction.
Momentum	The quantity of motion an object has, calculated as mass times velocity.
Acceleration	The rate at which an object’s velocity changes over time.

By understanding the definitions of these key terms, you’ll be able to approach problems with greater confidence and clarity. Regularly reviewing the terminology and using it in context will also help solidify your comprehension of the subject matter.

Tips for Mastering Problem Solving

Effective problem solving is a skill that requires practice, patience, and the ability to approach challenges systematically. While solving complex exercises may seem daunting at first, with the right strategies, you can simplify the process and improve your ability to tackle difficult problems. Developing a methodical approach, breaking down each step, and refining your analytical skills are all essential to mastering problem-solving techniques.

Here are several useful tips to help you excel in solving problems:

• Understand the Problem: Before attempting a solution, take the time to thoroughly read and comprehend the problem. Identify the knowns and unknowns, and make sure you understand what is being asked.
• Draw Diagrams: Visual aids, such as diagrams or graphs, can help you better understand the problem’s context and simplify the steps needed to solve it.
• Use the Right Formulas: Ensure that you’re using the correct formulas and concepts relevant to the problem. Don’t rely on memorization–always verify which formula fits the situation.
• Work Step-by-Step: Break down the problem into smaller, more manageable steps. Solving the problem incrementally helps avoid confusion and ensures you follow a logical process.
• Check Units: Always pay attention to the units involved in the calculations. Make sure that they are consistent throughout the process and convert them as needed to avoid errors.
• Review Your Solution: Once you arrive at an answer, take a moment to check your work. Ensure that the solution makes sense in the context of the problem and verify each step of your calculation.

By following these steps, you can enhance your problem-solving skills and increase your confidence in solving complex exercises. Consistent practice and reviewing your mistakes are key to becoming proficient at tackling problems efficiently and accurately.

How to Approach Conceptual Questions

When tackling questions that focus on fundamental principles, it’s essential to think beyond just the numbers and calculations. These types of problems require a deeper understanding of the concepts and how they relate to real-world scenarios. To successfully navigate these questions, it’s important to recognize the core ideas involved and approach them from a logical, step-by-step perspective.

The following strategies can help guide your thinking and improve your ability to solve these types of problems:

1. Grasp the Core Idea

Before diving into any equations or formulas, take a moment to understand the key concepts being tested. Focus on the underlying principles and how they are applied in the given situation. Often, these problems are more about the concept than the calculation itself.

2. Break the Problem Into Parts

Large, complex questions can often be broken down into simpler components. Identifying the different parts of the problem helps you address each concept individually and avoid feeling overwhelmed. Focus on one aspect at a time, then piece everything together at the end.

• Identify the key variables: Determine what is given and what needs to be found.
• Understand the relationships: Look for connections between the different factors in the problem.
• Think logically: How would the principles apply in real life? Use that logic to guide your reasoning.

By focusing on the principles and relationships involved, you can approach these problems with a clear understanding and solve them efficiently.

Remember, these problems are not just about memorizing formulas but about applying knowledge to analyze situations and make sense of them. With practice, you will be able to approach each problem with greater confidence and clarity.

Explaining Graphs and Diagrams

Graphs and diagrams are essential tools for understanding relationships between variables in scientific problems. They provide a visual representation of data, helping to clarify complex concepts and trends that may be difficult to grasp through text alone. By interpreting these visual aids correctly, one can extract meaningful insights and make more informed conclusions about the situation at hand.

When analyzing graphs and diagrams, it’s crucial to focus on the key elements, such as the axes, labels, scales, and any trends or patterns that emerge. A clear understanding of how to read these visuals will greatly enhance problem-solving skills and conceptual clarity.

Key Elements to Focus On

• Axes: Pay attention to the labels on the x and y axes. They typically represent the independent and dependent variables.
• Scale: Understand the units and intervals on both axes to interpret the magnitude of changes correctly.
• Trends: Look for patterns or slopes in the graph. These trends often indicate relationships such as direct or inverse proportionality.
• Data Points: Each point on a graph corresponds to a specific pair of values, illustrating how one variable changes in relation to the other.

Tips for Interpreting Diagrams

• Labeling: Ensure that all parts of the diagram are clearly labeled, including arrows, forces, or other relevant details.
• Key/Legend: Refer to the key or legend to understand the meaning of different symbols or colors used in the diagram.
• Units: Check the units of measurement for accuracy and consistency across the diagram.
• Context: Always consider the real-world context in which the diagram is applied to better understand its significance.

By breaking down the components of graphs and diagrams, you can enhance your ability to interpret scientific information effectively and use it to solve related problems. These visual tools are not just illustrations–they are essential aids for understanding how different variables interact in real-world scenarios.

Application of Principles in Real Life

The principles explored in scientific disciplines are not just confined to theoretical concepts–they play a vital role in the world around us. From the technology we use daily to the natural phenomena we observe, understanding these principles allows us to explain, predict, and influence the events that shape our environment. Whether it’s the motion of vehicles, the workings of electrical devices, or the behavior of natural forces, these principles have direct applications that impact our lives in profound ways.

By applying these ideas to real-world scenarios, we gain the ability to improve efficiency, solve everyday problems, and innovate in various fields. From improving transportation systems to advancing medical technologies, the influence of scientific concepts is ever-present and continually shaping the future.

Everyday Applications

• Transportation: Understanding motion, energy, and force helps optimize vehicle performance and improve safety features in cars, airplanes, and other modes of transport.
• Energy Use: Knowledge of energy conversion and efficiency guides the development of renewable energy sources and energy-saving technologies.
• Medical Devices: The application of concepts such as electromagnetism and fluid dynamics enables the design of advanced medical equipment like MRI machines and pacemakers.
• Communication: Principles of wave propagation and signal transmission are fundamental in creating communication systems, from radio broadcasts to modern wireless networks.

Technological Innovations

• Renewable Energy: Understanding the principles of thermodynamics and mechanics drives the development of more efficient solar panels and wind turbines.
• Space Exploration: The use of gravitational laws, motion, and thermodynamics has led to advancements in space travel and satellite technology.
• Electronics: The application of electrical principles is essential in the creation of consumer electronics such as smartphones, computers, and televisions.

In conclusion, the study of these core principles is crucial for both understanding the world and improving it. Their application not only solves immediate challenges but also opens doors to future innovations that will continue to enhance the quality of life globally.

Improving Your Performance

To enhance your ability in tackling complex problems, it’s essential to develop strong foundational skills and a deeper understanding of key principles. Successful learning relies on more than just memorizing facts–it involves practicing techniques, refining problem-solving strategies, and building a conceptual framework that allows you to apply knowledge effectively. By adopting structured methods and focusing on both theory and practice, you can significantly boost your performance and comprehension.

Improvement comes through consistent effort, proper planning, and the willingness to confront challenging material head-on. By focusing on the most effective techniques and adjusting your approach based on feedback, you can achieve mastery over time.

Key Strategies for Success

• Active Problem Solving: Engage with problems regularly to reinforce concepts and improve your analytical thinking.
• Conceptual Understanding: Aim to fully understand the core principles before moving on to more complex problems. This deep understanding will make it easier to apply knowledge in various contexts.
• Break Down Problems: Tackle complex problems step-by-step. This approach helps prevent feeling overwhelmed and ensures you don’t miss critical details.
• Time Management: Allocate specific time slots for learning, revision, and practice. This ensures a balanced approach to mastering different topics.

Effective Techniques for Improvement

Technique	Benefits
Practice Tests	Helps identify areas of weakness and builds confidence in problem-solving.
Group Study Sessions	Encourages collaboration, allowing for the exchange of ideas and better understanding.
Flashcards	Improves recall and reinforces important formulas and definitions.
Real-World Applications	Strengthens your understanding by showing how principles work in everyday situations.

In conclusion, improving your performance involves a combination of strategic learning, consistent practice, and an openness to refining your methods. By applying these techniques, you will not only gain a better grasp of the subject but also develop the skills necessary to approach any problem with confidence and clarity.

Reviewing Important Theories

Understanding key scientific concepts is fundamental to grasping how the world works. Theories serve as frameworks that help explain complex phenomena, offering insight into the relationships between different elements in nature. Revisiting these core ideas is crucial for deepening comprehension and applying them effectively in problem-solving. A strong grasp of these concepts provides the tools needed to approach real-world situations with precision and insight.

These theories not only explain observed behaviors but also predict future outcomes. Revising and solidifying this knowledge through careful review ensures a clear mental model, making it easier to tackle more advanced topics and challenges.

Essential Theories to Review

• Newton’s Laws of Motion: These fundamental principles describe how objects move under various forces, serving as the foundation for classical mechanics.
• Conservation Laws: The law of conservation of energy and momentum are pivotal in understanding how systems behave, particularly in closed environments.
• Electromagnetic Theory: Explains the behavior of electric and magnetic fields and their interactions with matter, which underpins many modern technologies.
• Thermodynamics: Describes the relationships between heat, energy, and work, offering insights into the operation of engines and energy systems.

Applications of Key Theories

• Newton’s Laws: Applied in engineering to design structures and predict the motion of vehicles or spacecraft.
• Conservation Laws: Used in collision analysis and understanding the transfer of energy in physical systems.
• Electromagnetic Theory: Integral to the development of electrical circuits, communication systems, and power generation.
• Thermodynamics: Crucial for understanding the efficiency of engines, refrigeration, and even biological processes.

By regularly reviewing and applying these core theories, you can improve both your theoretical knowledge and practical problem-solving skills. Reinforcing these concepts allows for a more intuitive understanding of the world, fostering a deeper appreciation for the underlying principles that govern it.

How to Prepare for Exams

Effective preparation is key to performing well in any examination. The goal is to ensure that you understand the core concepts, can solve related problems, and are familiar with the format and expectations of the test. A focused, structured approach can help you retain critical information and boost your confidence as you approach the exam day. By creating a well-organized study plan and practicing regularly, you can maximize your chances of success.

Preparation Steps

• Review Key Concepts: Focus on the most important theories and principles. Break down complex topics into manageable sections and make sure you fully understand the foundational ideas.
• Practice Problem Solving: Work through a variety of problems to reinforce your understanding and become comfortable with different question types.
• Use Study Aids: Take advantage of textbooks, online resources, or peer study groups to clarify difficult concepts and discuss problem-solving strategies.
• Create a Timetable: Allocate specific times for revision of each topic. Make sure to give extra time to areas that need improvement.

Test-Taking Strategies

• Stay Calm: During the exam, read each question carefully, and don’t rush. Take a few deep breaths to reduce stress.
• Manage Your Time: Plan how much time to spend on each section or question. Don’t linger too long on difficult questions; move on and return to them later if needed.
• Double-Check Work: If time permits, review your answers before submitting. Make sure you didn’t miss any steps or make careless mistakes.

Useful Tools for Preparation

Resource	Purpose
Textbooks	Provide comprehensive explanations and examples for core topics.
Practice Exams	Help familiarize you with the test format and types of questions.
Flashcards	Good for memorizing key terms and concepts quickly.
Study Groups	Allow discussion of difficult concepts and collaborative problem-solving.

By following these steps and strategies, you can improve your readiness and approach your exam with confidence. The key is consistent practice, understanding your weak points, and refining your problem-solving techniques.