
Mastering fundamental concepts in mathematics is essential for students to build a strong foundation. As learners advance, they are introduced to increasingly complex tasks that require clear reasoning and systematic approaches. The process of solving these problems can sometimes be challenging, but with the right strategies, it becomes an achievable goal.
By focusing on key strategies and providing step-by-step guidance, students can effectively tackle various exercises. Each lesson aims to improve problem-solving skills, encouraging critical thinking and perseverance. Understanding the core principles behind each question is crucial for not only completing tasks correctly but also for gaining confidence in the subject.
Students can benefit greatly from consistent practice, as repeated exposure to different types of problems helps reinforce understanding. Additionally, visual aids and practical examples make abstract ideas more accessible, ensuring that learners are well-prepared for more advanced challenges in the future.
Eureka Math Grade 5 Answers
This section focuses on providing solutions and step-by-step explanations for the various exercises encountered in elementary-level arithmetic. Students often face challenges when dealing with more complex problems, but understanding the core concepts behind each task can make a significant difference in how easily they are solved.
To improve problem-solving skills, it’s essential to break down each problem into smaller, manageable steps. This method not only helps in arriving at the correct solution but also fosters deeper understanding of the material.
- First, carefully analyze the problem statement.
- Next, identify the key information needed to solve the problem.
- Then, apply the appropriate techniques or formulas to find the solution.
- Finally, review the solution to ensure accuracy and consistency with the given data.
By practicing these steps regularly, students can build a solid understanding of how to approach similar challenges in the future. In this section, you’ll find a range of examples and detailed solutions designed to guide learners through each exercise.
- Start with simple examples to establish a clear understanding.
- Move to more complex problems once the foundational concepts are grasped.
- Use resources like diagrams, visual aids, and real-life scenarios to enhance comprehension.
Ultimately, the goal is to develop confidence in approaching tasks with the right mindset and techniques. By focusing on clarity and consistency, students can easily grasp the essential concepts and build a strong foundation for future learning.
Understanding Eureka Math Grade 5
At this level, students are introduced to a variety of important concepts that lay the foundation for more advanced problem-solving. The aim is to strengthen their ability to think critically, recognize patterns, and develop strategies for tackling a wide range of challenges. By exploring each concept step by step, learners are able to grasp the underlying principles that guide the subject matter.
Key Topics Covered

The curriculum focuses on several core areas, each building upon the previous to create a comprehensive understanding. Some of the most essential topics include:
- Fractions and Decimals
- Geometry and Shapes
- Measurement and Units
- Operations with Whole Numbers
- Word Problems and Logical Thinking
Approach to Learning
Understanding the approach to each problem is just as important as finding the solution itself. To achieve this, students are encouraged to:
- Analyze the problem carefully before jumping to conclusions.
- Look for patterns or relationships within the data.
- Break down complex problems into smaller, more manageable parts.
- Use visual aids and real-life examples to make abstract concepts more accessible.
By following this structured approach, students not only improve their problem-solving skills but also gain the confidence needed to tackle more challenging topics in the future.
Key Concepts in Grade 5 Math
At this level, students encounter essential topics that are vital for their mathematical development. The focus is on understanding relationships between numbers, operations, and geometric shapes, which will be built upon in later years. Grasping these concepts helps students improve their problem-solving abilities and logical reasoning skills, laying the groundwork for more advanced studies.
Some of the key areas covered include:
- Fractions: Understanding how to add, subtract, multiply, and divide fractions is a critical skill. Students also learn to convert between mixed numbers and improper fractions.
- Decimals: The relationship between decimals and fractions is explored, including how to compare and perform basic operations with decimal numbers.
- Geometry: Students study shapes, angles, and their properties. This includes calculating area, perimeter, and volume of different objects.
- Operations with Whole Numbers: Mastery of addition, subtraction, multiplication, and division using larger numbers is emphasized.
- Measurement: The use of standard units for measuring length, weight, and volume is introduced, along with converting between different units.
These concepts are not only foundational for future mathematical understanding but also help students apply their learning to real-world situations, preparing them for more complex challenges ahead.
How to Approach Eureka Math Problems
Tackling complex problems in elementary-level arithmetic requires a strategic approach that emphasizes clarity and logical reasoning. By breaking down each question into smaller, more manageable steps, students can avoid feeling overwhelmed and increase their chances of finding the correct solution. Understanding the problem fully is key to choosing the best method for solving it.
Step-by-Step Problem Solving
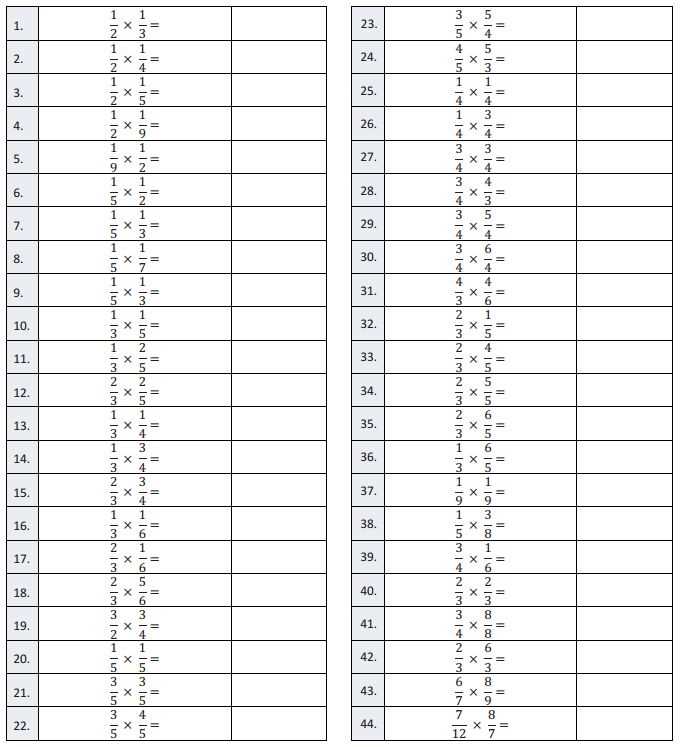
The most effective way to approach any exercise is by following a clear and systematic process. Start by:
- Reading the problem carefully: Ensure you understand the question before attempting a solution.
- Identifying key information: Look for the numbers, operations, and relationships that are relevant to the task.
- Choosing the right method: Select the appropriate strategy, whether it’s an operation, formula, or logical deduction.
- Solving step by step: Work through the problem one step at a time, checking each part as you go.
- Reviewing the solution: Once you’ve completed the steps, double-check your work to ensure accuracy.
Using Visual Aids and Tools
Visual representations such as diagrams, number lines, or models can help make abstract ideas clearer. These tools can simplify complex problems and provide students with a clearer path to the solution. Using resources like drawing shapes or listing steps in order helps ensure all aspects of the question are addressed.
By mastering these strategies, students can approach each new problem with confidence and improve their problem-solving abilities for future tasks.
Common Challenges in Grade 5 Math
At the elementary level, students often encounter a range of challenges that can make learning new concepts seem difficult. As the problems become more complex, it is natural for learners to struggle with certain aspects of the subject. However, with the right strategies and understanding, these obstacles can be overcome.
Some of the most common difficulties students face include:
- Understanding Fractions: Many students find fractions tricky, especially when it comes to comparing, adding, or subtracting them. The concept of parts of a whole can be confusing without a clear visual representation.
- Decimals and Their Relationships: Converting between decimals and fractions or performing operations with decimals is another area where students often need additional practice.
- Word Problems: Translating a word problem into a mathematical equation can be a challenge. Identifying key information and choosing the correct operation requires careful attention.
- Operations with Larger Numbers: As students work with bigger numbers, keeping track of operations and maintaining accuracy becomes more difficult. This includes multiplication and division with multi-digit numbers.
- Geometry and Spatial Thinking: Understanding shapes, angles, and spatial relationships can be difficult for students who have not yet developed a strong sense of geometry.
By addressing these common challenges through practice and guidance, students can gain the confidence they need to tackle more difficult problems in the future. Patience and persistence are key to mastering these concepts and building a solid foundation for future learning.
Step-by-Step Solutions for Grade 5

One of the most effective ways to master complex problems is by breaking them down into smaller, more manageable steps. This approach not only makes the task less overwhelming but also ensures that each part of the problem is addressed thoroughly. A systematic method of solving problems encourages students to focus on each individual component and enhances their understanding of the overall process.
Solving Word Problems
Word problems often seem challenging because they require students to translate text into numbers and operations. Here’s how to approach them:
- Read the problem carefully: Understand what is being asked and identify the important information.
- Choose the correct operation: Decide whether the problem requires addition, subtraction, multiplication, or division.
- Set up the equation: Translate the words into a mathematical expression using the numbers and operations identified.
- Solve step by step: Perform the operations in the correct order, checking your work after each step.
- Double-check the solution: Verify that the answer makes sense in the context of the problem.
Example: Solving a Fraction Problem
Let’s consider an example involving fractions:
- Problem: Add 3/4 and 5/8.
- Step 1: Find a common denominator. The least common denominator of 4 and 8 is 8.
- Step 2: Convert 3/4 to 6/8 so that both fractions have the same denominator.
- Step 3: Add the fractions: 6/8 + 5/8 = 11/8.
- Step 4: Simplify the fraction, if necessary. 11/8 is an improper fraction, which can be written as 1 3/8.
By following these step-by-step solutions, students can develop a structured approach to solving problems and gain confidence in their ability to handle more challenging tasks.
Helpful Tips for Solving Eureka Math
Successfully solving mathematical problems requires more than just applying formulas; it also involves strategic thinking and a clear approach. By following certain helpful techniques, students can simplify complex challenges and improve their problem-solving skills. These strategies can help learners stay organized, avoid mistakes, and gain confidence as they work through exercises.
Here are some useful tips to keep in mind when tackling mathematical problems:
- Read Carefully: Always read the problem multiple times to ensure full understanding. Pay close attention to keywords and details.
- Identify What is Being Asked: Before solving, identify the main question and determine what information is needed to find the answer.
- Break Down the Problem: Divide complex problems into smaller, simpler parts. Solve each part step by step to make it more manageable.
- Use Visual Aids: Draw diagrams, number lines, or models to visualize the problem. This can help make abstract concepts more concrete.
- Check Your Work: After completing each step, review your calculations and verify that they make sense in the context of the problem.
- Look for Patterns: Identify any recurring patterns or relationships between numbers that can help guide the solution process.
- Practice Regularly: Consistent practice is key to mastering new concepts. The more problems you solve, the easier it becomes to recognize patterns and apply techniques effectively.
By incorporating these tips into your problem-solving routine, you can approach each new challenge with confidence and clarity. Whether working on simple exercises or complex problems, these strategies will help you build a solid foundation for success.
Strategies for Mastering Grade 5 Topics
Successfully mastering the key topics in elementary education requires a combination of focused practice, effective study habits, and a clear understanding of each concept. When approaching new material, it’s important to develop a structured plan that encourages both comprehension and retention. With the right strategies, students can build a strong foundation for future learning and tackle even the most challenging problems with confidence.
Effective Practice Techniques
One of the best ways to master new topics is through consistent practice. Here are some methods to make your practice sessions more productive:
- Practice Regularly: Schedule regular study sessions to reinforce what you’ve learned and identify areas where more work is needed.
- Use a Variety of Resources: Work through different types of problems, including practice exercises, games, and worksheets to keep learning engaging and diverse.
- Start with the Basics: Focus on mastering fundamental concepts before moving on to more complex topics. This solid foundation will make it easier to understand advanced material.
Building Problem-Solving Skills
Problem-solving is a critical skill that extends beyond just memorizing facts. Here’s how to improve this skill:
- Break Down Problems: Analyze problems step by step. This helps to simplify complex questions and makes finding the solution more manageable.
- Learn from Mistakes: Don’t be afraid to make mistakes. Reviewing errors allows you to understand where you went wrong and how to correct your approach.
- Ask for Help When Needed: If a topic is particularly challenging, don’t hesitate to seek help from a teacher, tutor, or peer. Sometimes a different perspective can make all the difference.
By following these strategies, students can approach their lessons with greater confidence and a deeper understanding of the material, ultimately mastering the topics they encounter in the classroom.
Grade 5 Math Word Problems Explained
Word problems are a common and important aspect of elementary learning, requiring students to translate real-world situations into mathematical equations. These problems often present challenges because they involve reading comprehension, interpretation of information, and decision-making regarding the operations to use. However, with the right approach, word problems can be broken down into manageable steps and solved effectively.
Steps for Solving Word Problems
To tackle a word problem, follow these steps:
- Read the Problem Carefully: Ensure that you understand the entire scenario and what is being asked. Pay attention to key information.
- Highlight Important Data: Identify and underline numbers and important terms that help in solving the problem.
- Choose the Right Operation: Based on the context, decide whether to add, subtract, multiply, or divide.
- Set Up the Equation: Convert the word problem into a mathematical equation using the information you’ve gathered.
- Solve the Equation: Carry out the necessary operations in the correct order, and arrive at the solution.
- Check Your Answer: Re-read the problem and your solution to ensure the answer makes sense in the context of the question.
Example Word Problem
Let’s walk through an example to better understand how to solve a word problem:
| Problem | Solution Steps |
|---|---|
| Tom has 8 apples. He buys 5 more apples. How many apples does he have now? |
|
By following these simple steps, students can break down word problems into manageable pieces, making it easier to find the correct solution and boost their confidence in problem-solving.
Using Visual Aids in Eureka Math
Visual aids are powerful tools in the learning process, especially when it comes to complex concepts that require clear understanding. These tools help simplify abstract ideas by turning them into tangible, easy-to-understand representations. When students engage with visual aids, they can better grasp difficult topics and develop stronger problem-solving skills. Visual aids offer a way to make learning more interactive, accessible, and engaging, particularly for those who benefit from seeing concepts in action.
There are various types of visual aids that can be used to support learning. Some common examples include:
- Diagrams: Diagrams help students visualize relationships between numbers or shapes. They can illustrate geometric concepts, data sets, and operations in a clear and concise manner.
- Number Lines: Number lines are useful for understanding the concept of magnitude, comparing numbers, and performing operations such as addition and subtraction.
- Charts and Graphs: These visual tools make it easier to interpret numerical data, identify patterns, and compare different sets of information.
- Models: Physical models or manipulatives, such as blocks or counters, can be used to demonstrate abstract concepts, making them more concrete and relatable to students.
By incorporating visual aids into lessons, teachers can provide students with diverse ways to engage with the material, increasing their understanding and retention of key concepts. These tools not only make learning more interactive, but they also give students the opportunity to work through problems in a more hands-on, visual way.
How to Check Your Eureka Math Answers
Checking your work is an essential part of the learning process, ensuring that the solutions you arrive at are accurate and make sense. When working through problems, it’s important not just to find the answer but to verify that your approach was correct and that the result is reliable. There are several strategies that can help you effectively check your calculations and reasoning.
Step-by-Step Verification
To ensure that your solutions are correct, follow these steps:
- Revisit the Problem: Start by carefully reading the problem again to make sure you understood the question correctly. Pay attention to any details that may have been missed the first time.
- Check Your Operations: Verify that you used the correct mathematical operations. Review each step to confirm that you applied addition, subtraction, multiplication, or division as needed.
- Estimate the Result: Before performing the final calculation, make a rough estimate of the expected outcome. If your final answer seems too high or too low, it may indicate an error in your work.
- Reverse Your Steps: If possible, try working backwards from your final answer to see if you can return to the original problem. This can help confirm whether your solution makes sense.
Using Alternative Methods
If you’re unsure about your solution, try solving the problem using a different approach. For example, if you solved a word problem using subtraction, try using addition to cross-check the result. Sometimes, switching strategies can reveal mistakes or confirm that your answer is correct.
By using these methods, you can be more confident that your solutions are accurate, and you can improve your problem-solving skills over time. Regularly checking your work ensures that you understand the material deeply and are developing a reliable approach to tackling future problems.
Importance of Practice in Grade 5 Math
Consistent practice is crucial for mastering new concepts and improving problem-solving skills. In subjects that involve calculations and logic, frequent repetition allows students to reinforce what they have learned and build confidence in their abilities. The more problems a student works through, the better they become at recognizing patterns, applying strategies, and handling different types of questions.
Practice not only strengthens understanding but also develops a deeper connection to the material. When students engage with exercises on a regular basis, they become more efficient and start to approach problems with greater ease. This continuous repetition helps students move from a basic understanding to a level of proficiency where they can apply what they’ve learned in new and varied situations.
Benefits of Regular Practice:
- Improves Speed and Accuracy: By solving similar problems repeatedly, students can improve their speed and accuracy, allowing them to complete tasks more efficiently.
- Builds Confidence: Success through practice boosts self-confidence, helping students feel more capable and willing to tackle new challenges.
- Identifies Weak Areas: Regular practice helps students identify areas where they may need additional support or clarification, making it easier to focus on improving those areas.
- Enhances Retention: The more frequently students practice, the better they retain information, leading to long-term understanding rather than short-term memorization.
Incorporating daily or weekly practice sessions into the learning routine can have a significant impact on academic success. It encourages a growth mindset and ensures that students develop the skills they need to excel in problem-solving and critical thinking.
Effective Study Habits for Eureka Math
Developing good study habits is key to mastering any subject, especially when tackling complex concepts. Consistency, focus, and the right techniques can make a significant difference in how well students understand and apply what they’ve learned. Effective study habits not only help in retaining information but also improve problem-solving skills and increase academic confidence.
Creating a Productive Study Environment
A conducive learning environment is crucial for staying focused and organized. A quiet, distraction-free space with all necessary materials at hand can enhance concentration and reduce procrastination. Consider the following tips:
- Choose a Quiet Space: Select a study area where distractions are minimal, allowing full attention to the task at hand.
- Organize Study Materials: Keep textbooks, notebooks, and calculators readily accessible to avoid interruptions during study sessions.
- Set a Fixed Time: Designate a specific time each day for studying to establish a routine and promote consistency.
Active Learning Techniques
Simply reading through notes or watching videos may not be enough. Engaging actively with the content helps to deepen understanding and improve retention. Some effective study techniques include:
- Practice Regularly: Solve a variety of problems to reinforce concepts and identify areas for improvement.
- Teach Someone Else: Explaining concepts to others is a great way to solidify your understanding.
- Take Breaks: Short breaks between study sessions help maintain focus and prevent burnout.
- Use Visual Aids: Diagrams, charts, and visual representations can help clarify complex ideas and make learning more engaging.
By incorporating these study habits into your routine, you can enhance your understanding, increase your problem-solving efficiency, and ultimately achieve greater success in your academic journey.
Understanding Terminology in Grade 5 Learning
When tackling complex subjects, understanding the specific terminology used in lessons is critical for success. Terms are often designed to convey complex ideas in a simplified manner, but without a solid grasp of these key terms, students may struggle with comprehension and application. Developing a strong understanding of the language used throughout the curriculum helps students not only perform better but also boosts their confidence in approaching new topics.
Common Terms and Their Meanings
Familiarity with frequently used terms can make problem-solving and discussions easier. Here are some common terms encountered in lessons:
| Term | Definition |
|---|---|
| Equation | A mathematical statement that shows the equality between two expressions. |
| Variable | A symbol used to represent a number or value in an expression or equation. |
| Factor | A number or quantity that is multiplied by another to form a product. |
| Sum | The result of adding two or more numbers together. |
Why Understanding Terminology Matters
Knowing these terms ensures that students can follow instructions, understand problem-solving strategies, and communicate clearly in discussions. It also lays the foundation for more advanced concepts in future lessons. When students comprehend the language used in their lessons, they are better equipped to tackle problems independently and work through challenges with greater ease.
Resources for Additional Help in Learning
When facing challenges in understanding key concepts, having access to the right resources can make a significant difference in mastering the material. Various tools, websites, and support systems are available to reinforce learning and provide the extra assistance students need to succeed. These resources offer different types of support, from practice problems to instructional videos, and are designed to cater to various learning styles.
Online Platforms and Websites

Several websites provide interactive learning opportunities, allowing students to practice at their own pace. These platforms often include step-by-step solutions, video tutorials, and assessments that cater to specific topics. Some popular options include:
- Khan Academy: Offers free video lessons and exercises on a wide range of topics.
- IXL Learning: Provides interactive practice questions with immediate feedback.
- Prodigy: A game-based learning platform that covers many subjects and offers personalized learning paths.
Books and Workbooks for Practice
In addition to online tools, there are plenty of workbooks and practice books that provide exercises and explanations for common topics. These books break down complex problems into manageable steps, making them ideal for reinforcing concepts. Some recommended resources include:
- Workbooks from Scholastic: These provide clear explanations and plenty of practice exercises for various skill levels.
- Houghton Mifflin Harcourt Practice Books: A series of books that offer practice problems with detailed answers for students to check their work.
Using a combination of these resources can help strengthen a student’s understanding and boost their confidence in tackling challenging subjects.
How the Program Prepares for Future Learning
The educational approach taken at the elementary level sets the foundation for all future academic growth. By focusing on key principles and offering consistent opportunities for practice and application, students are well-equipped to tackle more advanced concepts in later stages of their education. The skills developed during these early years promote both critical thinking and problem-solving abilities, which are essential for success in higher levels of learning.
Building Strong Conceptual Understanding
At this stage, students are introduced to core concepts that they will build upon in future academic years. The curriculum ensures that children understand the “why” behind mathematical processes, not just the “how.” This deep comprehension provides a robust framework for more complex topics in the future. Key areas of focus include:
- Critical Thinking: Emphasizing reasoning and strategy helps children approach problems from different angles.
- Problem Solving: Building a systematic approach to solving challenges ensures students are prepared for more abstract thinking in later grades.
- Mathematical Communication: Encouraging students to explain their thinking and reasoning strengthens their ability to discuss and work through complex ideas.
Preparing for Advanced Topics
As students progress, they will encounter more sophisticated ideas and approaches that demand a solid foundation. The program nurtures a level of flexibility in thinking that enables students to adapt as they move to more advanced concepts. This prepares them for higher-level topics such as:
- Algebraic Thinking: Early exposure to patterns and relationships allows for smoother transitions into algebraic concepts.
- Fractions and Decimals: Mastering these concepts early on provides a critical foundation for future work with ratios, percentages, and proportional relationships.
- Data Analysis: As students grow, the ability to collect, interpret, and analyze data will become increasingly important, laying the groundwork for more advanced statistics and probability studies.
By ensuring a thorough understanding of essential concepts and promoting a problem-solving mindset, the program creates a pathway that helps students succeed not only in their current learning but also in their future academic journeys.
Why the Program Is Effective for Grade 5
The approach used in the curriculum for elementary learners offers a comprehensive, structured method for building essential skills. By integrating hands-on experiences, critical thinking, and problem-solving, it effectively prepares students for both immediate challenges and long-term academic success. The design of the program aligns with the developmental needs of young learners, ensuring that they grasp foundational concepts while gaining confidence in their abilities.
Key Features of the Program
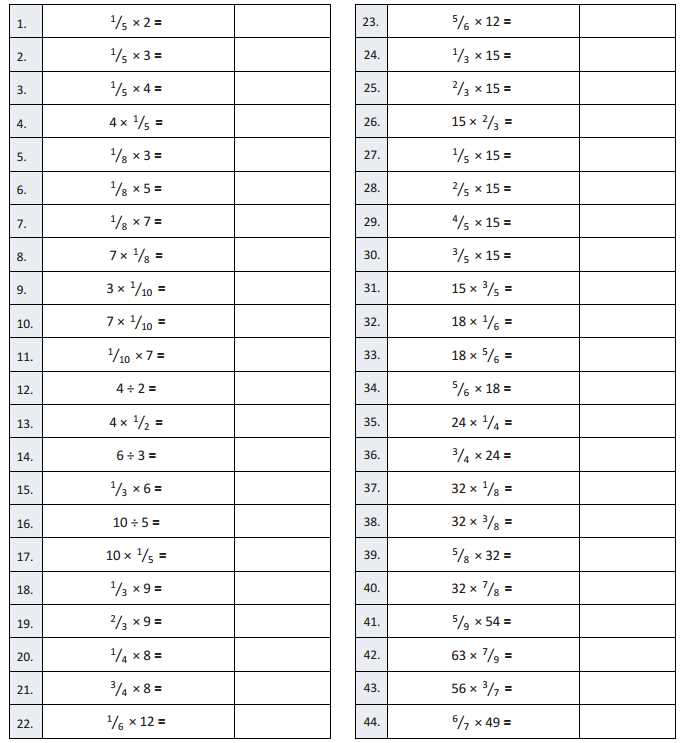
There are several reasons why this approach works well for students at this stage. It incorporates a variety of methods and strategies to engage students while ensuring that they develop a deep understanding of the core content. The program focuses on the following key features:
| Feature | Description |
|---|---|
| Conceptual Understanding | Emphasizes the “why” behind the process, allowing students to understand core concepts deeply, rather than just memorizing steps. |
| Progressive Difficulty | Starts with simple ideas and gradually introduces more complex ones, ensuring students are ready for more advanced topics as they progress. |
| Hands-on Activities | Encourages active participation through interactive tasks and problem-solving exercises, making learning more engaging and practical. |
| Real-Life Connections | Connects abstract concepts to everyday situations, helping students see the relevance of what they are learning and its application in real life. |
Benefits for Long-Term Learning
By focusing on critical thinking, comprehension, and application, this program lays a solid foundation that prepares students for future challenges. It promotes a growth mindset and encourages persistence when faced with difficult tasks. Additionally, students develop stronger problem-solving skills that they can apply across a range of subjects and real-world situations.
Overall, this approach supports students’ academic growth by making learning more interactive, relevant, and sustainable, ensuring they are well-prepared for future learning opportunities.