
Learning essential concepts in early education can sometimes be a challenge, especially when faced with complex problems. As students progress, they often need clear explanations and practical approaches to understand the material better. Whether it’s mastering number operations or understanding geometric shapes, a structured approach to learning can make a significant difference in their overall comprehension.
Support and practice are key components of success when tackling challenging exercises. By offering solutions that guide students step-by-step, we help them build confidence and enhance their problem-solving abilities. With a solid foundation, students can approach even the most difficult tasks with ease and assurance.
Effective learning techniques also play a crucial role in strengthening knowledge retention. A combination of repetition, visual aids, and hands-on practice ensures that concepts are not just understood but remembered for long-term success. This approach paves the way for mastering future subjects as students continue their educational journey.
5th Grade Go Math Answers

Achieving proficiency in key educational topics requires a thorough understanding of core concepts and consistent practice. This section provides solutions to a variety of exercises, designed to help students navigate through challenging tasks with confidence. By breaking down each problem and demonstrating clear step-by-step methods, students are equipped with the tools they need to succeed.
Through detailed explanations and well-structured approaches, learners can develop a deeper grasp of essential skills. These solutions are tailored to enhance comprehension, making complex problems easier to approach and solve. As students work through the examples, they gain valuable insights that foster both skill improvement and increased confidence in their abilities.
Understanding Go Math Curriculum
The educational framework in this program is designed to develop a deep understanding of fundamental concepts and problem-solving skills. It focuses on building a solid foundation through structured lessons and progressive challenges. The goal is to help students not only solve problems but also understand the underlying principles that make these solutions work.
Key Components of the Program
The curriculum is divided into several key areas, each aimed at strengthening different aspects of reasoning and calculation. These include number operations, measurement, and geometry, among others. Each section is carefully crafted to introduce concepts gradually, ensuring mastery before moving on to more complex topics.
Progression and Application

As learners advance through the lessons, they are encouraged to apply their knowledge in real-world scenarios, reinforcing their understanding and making the content more relatable. This practical approach helps bridge the gap between theoretical learning and everyday applications, making the educational journey both meaningful and engaging.
Key Concepts in 5th Grade Math

At this stage of education, students are introduced to more advanced concepts that lay the foundation for higher-level problem solving. Key ideas focus on refining basic skills while incorporating new topics that require deeper reasoning. The aim is to develop a well-rounded understanding that enables students to approach challenges with critical thinking and logical solutions.
Among the essential topics covered are fractions, decimals, and percentages, which are fundamental for many future applications. Students learn to perform operations with these values and understand how they relate to each other. Geometry and measurement are also emphasized, with students exploring shapes, area, volume, and units of measurement in practical contexts.
Another important area is data analysis and interpretation. Students are taught how to collect, organize, and analyze data, allowing them to make informed decisions based on their findings. These skills not only help in academics but are also valuable in real-life situations, where data-driven decisions are key to success.
Tips for Solving Word Problems
Word problems often challenge students to apply their understanding of concepts in practical situations. To solve these effectively, it is important to break down the information and identify what the problem is asking for. With the right strategies, even the most complex word problems become easier to tackle.
Step-by-Step Approach
- Read Carefully: Read the problem slowly and make sure to understand all the details before proceeding.
- Highlight Important Information: Identify key numbers, terms, and what the problem is asking you to find.
- Plan Your Strategy: Think about what operation or method is needed to solve the problem (e.g., addition, multiplication, division, etc.).
- Set Up the Equation: Translate the words into a mathematical equation or expression that can be solved.
- Check Your Work: Once you solve the problem, review the steps and ensure your solution makes sense in the context of the problem.
Common Pitfalls to Avoid
- Ignoring Units: Always pay attention to the units of measurement (e.g., inches, liters, dollars) to avoid errors in conversion.
- Rushing Through the Problem: Taking time to carefully read and think through each step can prevent mistakes.
- Overcomplicating the Problem: Simplify the problem by breaking it down into smaller, manageable parts.
How to Tackle Fractions Effectively
Understanding fractions can be challenging, but with the right approach, they become much easier to handle. The key to mastering fractions is breaking them down into simpler steps and practicing consistently. By developing a clear strategy for working with fractions, students can solve problems with confidence and accuracy.
Key Strategies for Fractions
- Find Common Denominators: When adding or subtracting fractions, it is essential to convert them to a common denominator first.
- Simplify Fractions: Always simplify fractions to their lowest terms by dividing both the numerator and denominator by their greatest common divisor (GCD).
- Convert Fractions to Decimals: Sometimes it’s easier to work with fractions by converting them into decimals, especially for comparison or calculation purposes.
- Multiply Across: When multiplying fractions, multiply the numerators together and the denominators together. Simplify the result if needed.
- Practice Visualizing: Drawing pictures or using fraction strips can help visualize the relationship between parts and wholes, making it easier to grasp concepts.
Common Mistakes to Avoid
- Skipping Simplification: Neglecting to simplify fractions can lead to unnecessarily complex answers.
- Mixing Operations: Ensure that the correct operation (addition, subtraction, multiplication, or division) is used for the correct type of problem.
- Forgetting to Convert: Always remember to convert fractions to a common denominator or into decimals when necessary.
Mastering Decimal Operations
Working with decimals is an essential skill that opens the door to many advanced concepts in mathematics and real-life applications. By understanding how to perform operations with decimal numbers, students can confidently solve a wide range of problems. The key to success is mastering the basic rules and practicing consistently to improve accuracy and speed.
Essential Steps for Decimal Operations
- Align the Decimal Points: Always line up the decimal points when adding or subtracting decimals to ensure accurate results.
- Use Place Value When Multiplying: When multiplying decimals, count the total number of decimal places in both numbers and place the decimal point accordingly in the result.
- Divide with Precision: When dividing decimals, convert the divisor into a whole number by moving the decimal point and adjust the dividend accordingly.
- Estimate First: Estimating the result before performing the actual operation can help catch errors and provide a sense of whether the final answer is reasonable.
Common Pitfalls to Watch Out For
- Misplacing the Decimal: One of the most common errors when working with decimals is incorrectly placing the decimal point after performing an operation.
- Overlooking Decimal Places: Pay careful attention to the number of decimal places involved, especially when multiplying or dividing.
- Skipping Steps: Avoid rushing through calculations and ensure each step is carefully followed to maintain accuracy.
Understanding Geometry and Shapes
Geometry and shapes are fundamental concepts that help students understand the world around them. By studying different forms and their properties, learners can gain insights into spatial relationships and measurement. This knowledge is not only important for academic success but also for practical applications in everyday life, such as design, construction, and navigation.
To understand shapes, it’s essential to recognize their characteristics, such as sides, angles, and symmetry. Whether it’s a simple square or a more complex polygon, each shape has its own set of rules and formulas that determine its properties. Below is a table summarizing some basic shapes and their key features:
| Shape | Sides | Angles | Key Properties |
|---|---|---|---|
| Triangle | 3 | 3 angles | Sum of angles = 180° |
| Square | 4 | 4 right angles | All sides equal, opposite sides parallel |
| Circle | 0 | No angles | Constant radius, all points equidistant from center |
| Rectangle | 4 | 4 right angles | Opposite sides equal, opposite sides parallel |
| Pentagon | 5 | 5 angles | Sum of angles = 540° |
Helpful Strategies for Multiplication
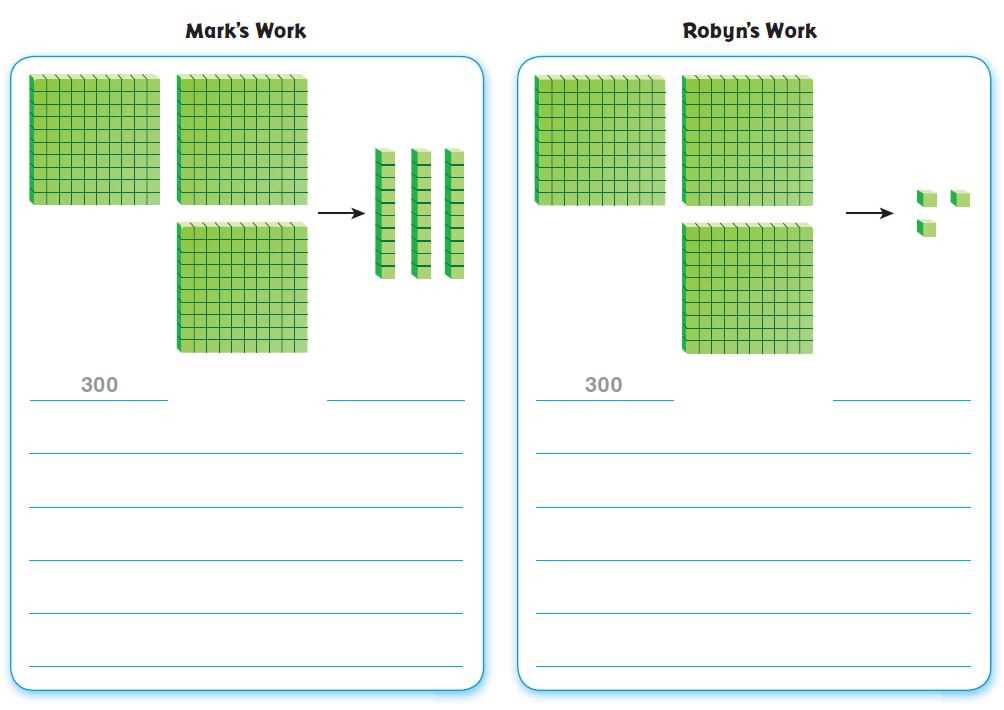
Mastering multiplication is essential for solving a wide range of problems, both in academics and in real-life situations. The key to becoming proficient in multiplication is learning to approach it in an organized and efficient way. By using various strategies, students can simplify the process and tackle even complex problems with ease.
One effective method is breaking down larger problems into smaller, more manageable parts. For example, multiplying by splitting numbers into tens and ones, or using the distributive property, allows students to focus on simpler calculations before combining the results. Visualization techniques, such as using arrays or number lines, can also help reinforce understanding and improve recall speed.
Another useful strategy involves memorization of key multiplication facts, which can be supported by practice through games or flashcards. The more familiar students become with basic multiplication tables, the faster and more confidently they can solve problems. Additionally, practicing estimation helps check the reasonableness of answers and improves overall number sense.
Division Techniques for 5th Graders
Understanding division is crucial for developing problem-solving skills and mathematical fluency. The process involves splitting numbers into equal parts, and learning efficient strategies for division can greatly improve accuracy and confidence. Whether handling simple or more complex division problems, there are various methods to simplify the task and make the process easier to grasp.
Key Division Methods
- Long Division: This traditional method breaks down the division into manageable steps, helping students work through each part of the problem systematically.
- Partial Quotients: This strategy allows students to divide in chunks, making it easier to handle larger numbers by subtracting parts of the divisor from the dividend.
- Estimation: Estimating the quotient first can help verify the final answer and make the process more intuitive.
- Using Multiplication Facts: Understanding how multiplication relates to division helps in quick mental calculations and verifying results.
Important Tips to Remember
| Tip | Description |
|---|---|
| Always Check Remainders | When dividing, make sure to check the remainder for any leftover numbers that don’t fit into the division. |
| Estimate Before You Divide | Estimating the answer can give you an idea of what the result should be, making it easier to spot mistakes. |
| Practice Division Facts | Familiarity with basic division facts can speed up the process and improve overall efficiency in solving problems. |
| Break Down Large Problems | For larger numbers, break the division down into smaller, more manageable parts to avoid confusion. |
Improving Measurement Skills in Math
Mastering measurement is a fundamental part of building strong mathematical abilities. It involves understanding the size, length, volume, and weight of objects, and knowing how to apply these concepts in different situations. By practicing measurement techniques and gaining familiarity with various units, students can improve their ability to solve problems accurately and efficiently.
One effective way to enhance measurement skills is by using real-world examples. For instance, measuring everyday items like books, water bottles, or rooms in a house helps students make the connection between abstract numbers and tangible objects. Familiarity with both customary and metric units is also important for versatility, as different situations may require different systems of measurement.
Additionally, understanding how to estimate measurements can greatly improve problem-solving efficiency. Estimation helps provide a rough idea of the expected result, allowing for quick checks of accuracy. Regular practice with different types of problems will increase confidence and fluency, making measurement tasks easier to handle over time.
Handling Data and Graphing Basics
Understanding how to collect, organize, and represent data is an essential skill for interpreting information and making informed decisions. By learning the basics of data handling and graphing, students can better visualize relationships between numbers, identify trends, and draw conclusions from sets of information. Whether it’s organizing survey results or tracking changes over time, graphing provides a powerful tool for illustrating data in a clear and meaningful way.
There are several types of graphs and charts that help represent data, each suitable for different kinds of information. Bar graphs, line graphs, and pie charts are some of the most common methods used to display data visually. By practicing how to create and read these graphs, students will gain a deeper understanding of how data can be summarized and analyzed effectively.
To begin graphing, it is crucial to understand key concepts such as the x-axis and y-axis on a coordinate plane, as well as how to label data points accurately. Knowing how to interpret the information presented in a graph helps students make sense of complex data and use it to support arguments or findings. Regular practice with creating and analyzing different types of graphs will enhance data literacy and improve problem-solving skills.
Exploring Patterns and Sequences
Recognizing patterns and sequences is a key skill in developing logical thinking and problem-solving abilities. These patterns, whether they involve numbers, shapes, or even everyday events, provide structure and predictability, making complex concepts easier to understand. By identifying and continuing sequences, students can strengthen their ability to anticipate future values and relationships, which is fundamental in many areas of study.
Patterns can appear in a variety of forms, such as arithmetic sequences, geometric shapes, or repeating cycles. By understanding how to recognize the underlying rule governing a sequence, students can easily predict the next elements and solve related problems. Whether it’s adding a fixed number each time or multiplying by a constant, these operations form the foundation of more advanced concepts in algebra and beyond.
Developing fluency with sequences involves practice, as well as the ability to generalize patterns to new contexts. As students become more familiar with different types of sequences, they can begin to apply this knowledge to solve real-world problems, such as calculating the total cost of items over time or predicting future events based on established trends.
Problem-Solving Methods for Success
Effective problem-solving requires a structured approach to break down complex challenges into manageable steps. By using various strategies, students can develop the skills needed to approach difficult tasks with confidence and clarity. These methods help in organizing thoughts, identifying key elements of the problem, and determining the most efficient path to a solution.
Key Steps in Problem-Solving
When facing a challenging question, follow these essential steps to reach a solution:
- Understand the problem: Read the problem carefully to make sure you comprehend all the details.
- Devise a plan: Break down the problem into smaller, simpler steps or choose a strategy to solve it.
- Carry out the plan: Execute the steps methodically, checking each along the way.
- Review and reflect: Once a solution is found, review the process to ensure the answer makes sense and is accurate.
Helpful Strategies
In addition to following the steps, certain techniques can further improve problem-solving abilities:
- Look for patterns: Identifying recurring themes or numbers can make solving the problem easier.
- Draw diagrams: Visualizing the problem through pictures or charts helps to better understand relationships and structures.
- Work backward: Start from the desired outcome and reverse the steps to find a solution.
- Estimate: Make an educated guess before diving into complex calculations to check if your final answer seems reasonable.
By practicing these methods, students can sharpen their critical thinking abilities, improving both their academic performance and their ability to tackle real-world problems with ease.
Working with Exponents and Powers
Exponents and powers are essential concepts that allow for the simplification of large numbers and the expression of repeated multiplication. By using exponents, students can express large calculations in a more manageable and efficient form. Understanding how to work with powers provides the foundation for more complex mathematical operations and helps to solve problems that involve scaling, area, volume, and scientific notation.
Understanding the Basics
Exponents represent the number of times a base number is multiplied by itself. The base is the number being multiplied, and the exponent tells you how many times to multiply that base. For example, in the expression 34, 3 is the base and 4 is the exponent, which means multiplying 3 by itself four times (3 × 3 × 3 × 3).
Key Properties of Exponents
- Product of powers: When multiplying numbers with the same base, add the exponents. Example: am × an = am+n.
- Quotient of powers: When dividing numbers with the same base, subtract the exponents. Example: am ÷ an = am-n.
- Power of a power: When raising an exponent to another exponent, multiply the exponents. Example: (am)n = am×n.
- Power of a product: Distribute the exponent over multiplication. Example: (ab)n = an × bn.
- Zero exponent: Any non-zero number raised to the power of zero is 1. Example: a0 = 1.
By practicing these rules and applying them to real-life situations, students can improve their ability to work with exponents, simplifying complex calculations and gaining deeper insight into the power of numbers.
Building Confidence in Math Concepts

Confidence in mathematical abilities is a crucial part of achieving success in learning and applying key concepts. Many students struggle with certain topics, but with the right approach, they can overcome these challenges and gain a deeper understanding. Developing confidence comes from consistent practice, breaking down complex problems into simpler steps, and seeing progress over time. When students feel capable, they are more motivated to tackle new challenges and improve their problem-solving skills.
Steps to Build Confidence
- Start with the Basics: Ensure a strong understanding of foundational concepts before moving on to more difficult topics. Mastery of basic operations makes advanced problems easier to solve.
- Practice Regularly: Repetition is key. Regular practice helps reinforce skills and builds familiarity, making problems less intimidating.
- Break Down Problems: Encourage students to approach complex problems step by step. Breaking down larger problems into manageable parts boosts confidence and reduces anxiety.
- Positive Reinforcement: Praise effort and progress, not just results. Positive reinforcement helps students recognize their growth, which strengthens their self-belief.
- Embrace Mistakes: Mistakes are part of the learning process. Teach students to view errors as opportunities to learn and improve rather than setbacks.
Techniques for Overcoming Challenges
- Visual Aids: Use diagrams, charts, and visual tools to help students better understand abstract concepts and solve problems with confidence.
- Collaborative Learning: Encourage group work or pair learning to create a supportive environment where students can share strategies and gain different perspectives.
- Real-Life Applications: Show how math concepts apply to real-world scenarios. This can help students see the relevance of what they are learning and increase their motivation.
Building confidence in mathematical skills takes time and persistence, but with the right strategies in place, students can achieve success and feel proud of their accomplishments.
Why Practice Makes Perfect in Math

Mastery of any skill, particularly in solving numerical problems, is achieved through consistent practice. When faced with new concepts, it’s easy to feel overwhelmed, but practice allows individuals to reinforce their understanding and improve their problem-solving strategies. The more time spent working through different types of problems, the more familiar and manageable they become. This repetition builds confidence and proficiency, allowing students to tackle even the most complex challenges with ease.
Benefits of Regular Practice
- Improved Retention: Regular practice helps solidify concepts in long-term memory, making them easier to recall when needed.
- Faster Problem Solving: The more problems a student works through, the quicker they become at recognizing patterns and applying the appropriate strategies.
- Increased Confidence: Successfully solving problems builds self-belief, motivating students to tackle more difficult tasks.
- Better Error Recognition: Practice helps identify common mistakes, allowing students to correct them and avoid repeating them in the future.
How Practice Leads to Perfection
| Concept | Effect of Practice |
|---|---|
| Basic Operations | Repetition leads to speed and accuracy, turning simple calculations into second nature. |
| Problem-Solving Techniques | Practicing different types of problems builds a toolkit of strategies that can be applied to new challenges. |
| Complex Calculations | With enough practice, students become comfortable with advanced steps and are less likely to make errors under pressure. |
Ultimately, practice makes the process of learning smoother and more enjoyable, as students feel more capable and equipped to handle a variety of problems. By committing to regular practice, learners can continue to refine their skills and work toward mastery, knowing that each attempt brings them closer to perfection.
Resources for Extra Help
When faced with challenges in understanding certain concepts, it’s important to know where to turn for additional support. There are a variety of resources available that can provide extra assistance, whether through online platforms, books, or personal tutoring. These tools can help reinforce what has already been learned and offer different approaches to mastering difficult topics. Finding the right resource can make all the difference in building confidence and improving skills.
Online Platforms offer a wide range of interactive tools and tutorials that cater to different learning styles. Websites like Khan Academy and IXL provide practice exercises, video lessons, and detailed explanations, allowing learners to progress at their own pace. These platforms often cover a broad range of topics, from basic to advanced, and are an excellent resource for those who prefer self-paced learning.
Tutoring Services are another valuable option for those who need one-on-one assistance. Whether in-person or virtual, a tutor can provide personalized help and focus on areas where a student is struggling. Many schools offer tutoring sessions, and there are also private services available. Tutors can break down complex concepts into simpler steps, ensuring a deeper understanding.
Books and Guides can also serve as a great supplementary resource. Practice workbooks often contain a wide variety of problems and step-by-step solutions, which allow students to work through exercises independently. Guides such as Math for Dummies or The Everything Guide to Math are excellent for those who prefer reading and studying at their own pace.
Ultimately, the key to success is persistence, and with the help of these resources, students can feel empowered to overcome obstacles and strengthen their problem-solving abilities. Whether it’s online tutorials, a tutor’s guidance, or self-study with books, there’s always an option to enhance learning and gain mastery over complex concepts.