Preparing for an upcoming test in advanced mathematics requires a solid understanding of key concepts and effective strategies for tackling complex problems. Whether you’re aiming to improve your problem-solving speed or strengthen your understanding of specific topics, a focused approach can make a significant difference.
In this section, we will explore various mathematical techniques, covering a wide range of topics that commonly appear in higher-level assessments. By practicing essential skills and familiarizing yourself with the types of challenges you may encounter, you’ll be well-equipped to approach the test with confidence.
Mastering the material involves not just knowing the theoretical aspects but also being able to apply them practically. Emphasizing problem-solving exercises, logical reasoning, and the ability to analyze different types of questions will enhance your readiness. With the right mindset and preparation, achieving success is entirely within reach.
Key Concepts for Mathematical Mastery

Successfully preparing for a mathematics assessment involves revisiting and reinforcing the core principles that are commonly tested. Mastery of these fundamental concepts is essential to solving a wide variety of problems that may appear during the test. By understanding the methods and procedures for approaching each type of challenge, you can increase your chances of performing well.
Essential Topics for Problem Solving
Focus on areas such as equations, functions, and graph analysis. Whether it’s simplifying complex expressions or solving for unknown variables, these topics are central to most problems. Additionally, learning how to manipulate and work with different types of equations–such as quadratic or rational–will provide you with the tools needed to handle diverse scenarios effectively.
Approach to Practice and Application

Repetition is key to reinforcing concepts. Work through practice problems, starting with simpler tasks and gradually progressing to more complex ones. This will help build both speed and accuracy in applying mathematical techniques. Over time, patterns and strategies will become more familiar, allowing for a more confident approach when facing a variety of problems in the assessment.
Essential Algebra 2 Concepts to Master

To succeed in higher-level mathematics, it is crucial to focus on a variety of key principles that are commonly tested. These concepts provide the foundation for solving complex problems and offer the tools necessary to approach a wide range of challenges. Mastering these topics will not only help in exams but also improve problem-solving abilities in real-world applications.
The following areas are fundamental and should be thoroughly understood:
- Equations and Inequalities: Mastery of linear, quadratic, and rational equations, as well as systems of inequalities, is essential for solving problems efficiently.
- Functions and Graphs: Understanding how to interpret, manipulate, and graph various types of functions, such as exponential and logarithmic, is crucial for success.
- Polynomials: Learn how to work with polynomials, including factoring, simplifying expressions, and solving polynomial equations.
- Rational Expressions: Grasp how to simplify, multiply, divide, and solve rational expressions and equations.
- Sequences and Series: A strong grasp of arithmetic and geometric sequences, as well as series, will help solve complex problems more easily.
By focusing on these critical concepts, you can strengthen your mathematical foundation and be better prepared for tackling the challenges that lie ahead.
Key Strategies for Preparation
Effective preparation is the key to achieving success in any challenging assessment. By adopting a structured approach and focusing on the most important areas, you can ensure that you’re ready for the test. Consistent practice, time management, and strategic study techniques will make the process more efficient and less overwhelming.
Effective Study Methods
To prepare efficiently, consider the following strategies:
- Practice Regularly: Work through a variety of problems daily to reinforce your understanding of key topics and techniques.
- Break Down Complex Problems: Approach difficult questions step by step. Breaking them down into smaller parts can help you focus and solve them more easily.
- Review Mistakes: Spend time analyzing errors and understanding why they occurred. This helps you avoid repeating them in the future.
- Use Practice Tests: Simulate real test conditions by taking timed practice tests. This helps build confidence and manage time effectively during the actual assessment.
Time Management Tips
Organizing your time effectively can make a huge difference in your preparation:
- Create a Study Schedule: Plan your study sessions in advance, allocating more time to difficult areas while ensuring you cover all necessary topics.
- Avoid Cramming: Spread out your study sessions over time to reinforce your memory and avoid last-minute stress.
- Take Breaks: Schedule short breaks during your study sessions to maintain focus and prevent burnout.
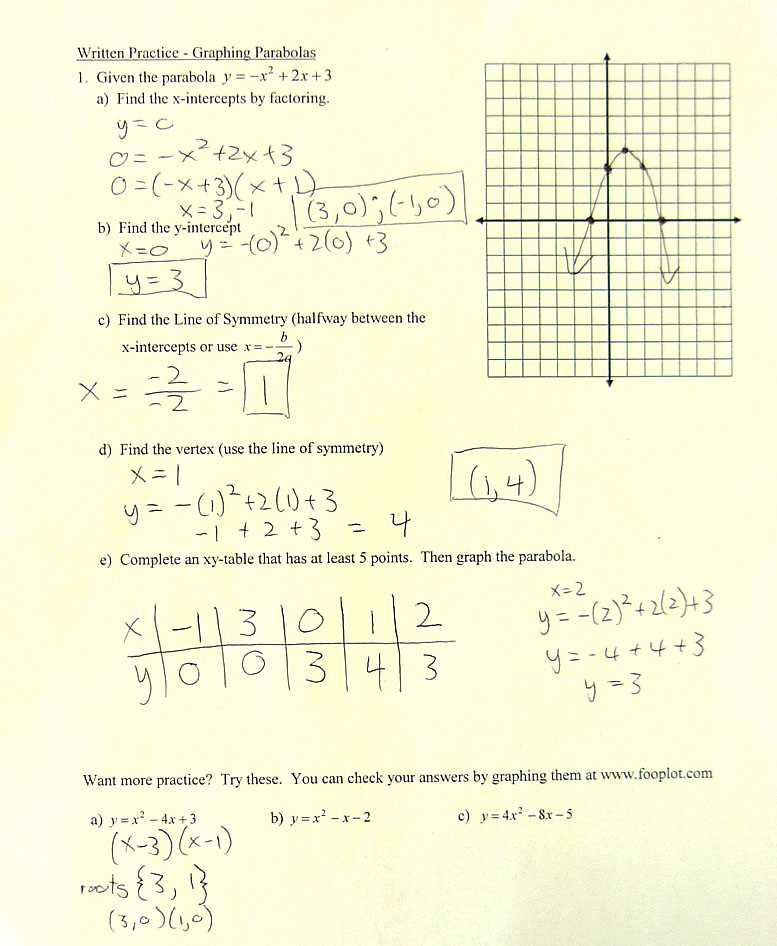
Understanding Quadratic Equations in Depth
Quadratic equations are a fundamental topic in mathematics that require a deep understanding to solve effectively. These equations involve variables raised to the second power and are commonly encountered in a wide range of problems. Mastering the methods for solving these types of equations will significantly enhance your problem-solving ability and boost your confidence in handling more complex scenarios.
One of the key approaches to solving quadratic equations is recognizing their standard form, which typically appears as ax² + bx + c = 0. From this point, there are several techniques that can be applied, such as factoring, completing the square, or using the quadratic formula. Each method has its advantages depending on the nature of the equation, and knowing when and how to apply each method is essential for efficiency.
Factoring is often the simplest method when the equation is factorable, allowing you to express the quadratic as a product of two binomials. For more complex equations, completing the square can help rewrite the equation in a perfect square form, leading to an easy solution. If these methods are not applicable, the quadratic formula provides a general solution for any quadratic equation, offering an exact answer every time.
By developing a strong grasp of these techniques and practicing a variety of problems, you’ll be well-equipped to tackle quadratic equations with ease and precision.
Solving Systems of Equations Effectively
Solving systems of equations is an essential skill in mathematics that allows you to find the values of variables that satisfy multiple conditions simultaneously. Whether dealing with two or more equations, understanding the most effective methods for solving these systems is crucial for success. The ability to solve systems efficiently is valuable in both academic and practical contexts, especially in fields like engineering and economics.
Methods for Solving Systems
There are several approaches for solving systems of equations, each useful in different situations:
- Substitution Method: This method involves solving one of the equations for one variable and then substituting that expression into the other equation. It’s ideal when one equation can be easily solved for a single variable.
- Elimination Method: This approach involves adding or subtracting equations to eliminate one of the variables. It’s often faster when the coefficients of one variable are already set up to cancel each other out.
- Graphical Method: By plotting both equations on a graph, you can visually identify the point where the lines intersect, which corresponds to the solution. This method is useful for understanding the relationship between the equations but is less precise than algebraic methods.
Choosing the Right Approach
The best method depends on the complexity and structure of the system. If one equation is easily solvable for a variable, substitution may be the most efficient. If the system involves larger numbers or more variables, elimination can be a quicker approach. For simpler systems or visual understanding, the graphical method provides an intuitive solution. By practicing these techniques, you’ll be able to select the most effective method for any given system.
Mastering Polynomial Functions and Operations

Polynomial functions are a cornerstone of advanced mathematics, playing a critical role in many areas of study. Mastering these functions and understanding how to manipulate them is essential for solving a wide variety of mathematical problems. By learning how to perform operations such as addition, subtraction, multiplication, and division, you can confidently tackle more complex equations and expressions.
Polynomials are composed of terms that include variables raised to whole-number exponents. Operations on polynomials require careful attention to the rules governing exponents and coefficients. Whether simplifying an expression or factoring a polynomial, knowing the correct methods is key to achieving accurate results.
| Operation | Description | Example |
|---|---|---|
| Addition | Combine like terms by adding the coefficients of terms with the same degree. | (3x² + 4x) + (5x² – 2x) = 8x² + 2x |
| Subtraction | Subtract the coefficients of like terms, distributing the negative sign across the terms. | (6x³ + 2x) – (3x³ + 5x) = 3x³ – 3x |
| Multiplication | Multiply each term in the first polynomial by every term in the second polynomial, then combine like terms. | (2x + 3)(x – 4) = 2x² – 5x – 12 |
| Division | Divide each term in the polynomial by the divisor, similar to long division. | (4x² + 2x) ÷ (2x) = 2x + 1 |
By practicing these operations and understanding how to apply them to various types of polynomial expressions, you’ll be well-equipped to handle increasingly difficult problems and deepen your understanding of mathematical concepts.
Analyzing Rational Expressions and Equations
Understanding how to work with rational expressions and equations is a crucial skill in mathematics. These expressions involve ratios of polynomials and require a different approach than simple polynomial equations. By mastering how to simplify, solve, and manipulate these expressions, you’ll be better equipped to handle a wide variety of problems.
Simplifying Rational Expressions

Simplifying rational expressions often involves factoring both the numerator and denominator and canceling out common factors. It’s important to remember that any factor in the denominator that equals zero must be excluded from the domain of the expression. Here are the steps for simplifying:
- Factor both the numerator and denominator.
- Cancel out any common factors between the numerator and denominator.
- Check for restrictions by identifying values of the variable that make the denominator equal to zero.
Solving Rational Equations
Rational equations require additional steps to solve. First, you must eliminate the fractions by multiplying through by the least common denominator (LCD). Then, solve the resulting equation as you would any other algebraic equation. Be cautious about extraneous solutions that may arise during the process.
- Multiply both sides of the equation by the LCD.
- Solve the resulting equation for the variable.
- Check for extraneous solutions by substituting the solutions back into the original equation.
By practicing these methods, you can improve your ability to handle rational expressions and equations with confidence and accuracy.
Tips for Tackling Exponential Functions
Exponential functions are a key concept in mathematics that describe growth or decay patterns, making them essential in various real-world applications such as population growth, compound interest, and radioactive decay. Understanding how to work with these functions can greatly enhance your problem-solving skills, especially when dealing with equations involving exponents.
One of the first things to recognize is the structure of exponential functions, typically written as f(x) = a * b^x, where a represents the initial value, b is the base, and x is the exponent. The behavior of the function depends heavily on the base b>. If b > 1, the function grows exponentially, and if 0 , the function decays exponentially.
When solving exponential equations, it’s helpful to apply logarithms. This allows you to “bring down” the exponent, transforming the equation into a form that can be solved more easily. Additionally, recognizing key properties of exponents, such as b^m * b^n = b^(m+n), can simplify the manipulation of these functions.
To effectively handle these types of problems, practice solving for unknown variables in the exponent, and get familiar with using logarithms to reverse exponential operations. This approach will help you solve exponential equations with greater accuracy and efficiency.
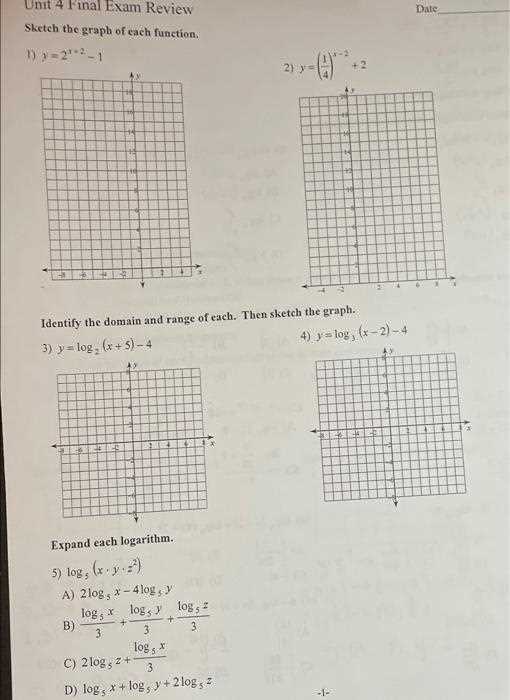
Logarithms and Their Real-World Applications
Logarithms are mathematical tools that help simplify complex exponential relationships by providing a way to solve equations where the variable appears as an exponent. In many real-world scenarios, logarithms are used to model processes that involve growth, decay, or scaling, such as in finance, science, and engineering.
Understanding how logarithms work can provide insight into phenomena such as population growth, earthquake intensity, and sound intensity. The logarithmic scale makes it easier to work with very large or small numbers, which are common in these fields.
One of the most common applications is in measuring the pH level of a solution, which is based on the logarithmic scale, or in calculating compound interest in finance. Below is a table showcasing a few key applications of logarithms in real-world contexts:
| Application | Description | Formula |
|---|---|---|
| pH Level | Used to measure the acidity or alkalinity of a solution. The pH scale is logarithmic, where each unit change represents a tenfold change in acidity. | pH = -log[H+] |
| Compound Interest | Logarithms help solve for the time required to reach a certain investment value when interest is compounded. | A = P(1 + r/n)^(nt) |
| Earthquake Magnitude | The Richter scale, which measures earthquake magnitudes, is logarithmic. Each whole number increase represents a tenfold increase in amplitude. | M = log10(A/T) |
| Sound Intensity | Sound levels are often measured in decibels, which are based on a logarithmic scale. | dB = 10 * log10(I/I0) |
By understanding the properties of logarithms and how they are applied in these practical situations, you can tackle problems that involve exponential growth or decay more effectively. Whether working with large datasets or solving for unknowns in scientific formulas, logarithms provide a powerful and efficient tool for analysis.
Working with Sequences and Series
Sequences and series are fundamental concepts in mathematics, essential for understanding patterns and relationships between numbers. Sequences involve ordered lists of numbers, while series represent the sum of these numbers. These ideas have widespread applications, from calculating interest in finance to modeling real-world phenomena like population growth or the spread of diseases.
Understanding Sequences
A sequence is a list of numbers arranged in a specific order. The numbers in a sequence are called terms, and the pattern that governs the sequence determines how each term is generated. For example, in an arithmetic sequence, the difference between consecutive terms is constant, while in a geometric sequence, each term is found by multiplying the previous term by a constant factor. Recognizing these patterns helps in solving problems related to rates of change, growth, and decay.
Working with Series
A series is the sum of the terms of a sequence. There are two main types of series: finite and infinite. In a finite series, the sum of a set number of terms is calculated, whereas an infinite series continues indefinitely. To calculate the sum of a series, you can apply various formulas, depending on whether the sequence is arithmetic or geometric. Understanding these formulas makes it easier to solve for the sum of terms quickly, whether in a simple case or more complex applications.
By mastering sequences and series, you can solve problems that involve summing values over time, such as calculating the total interest in a savings account, or determining the total distance traveled by an object moving at increasing speeds. These concepts are critical tools for mathematical problem-solving and analysis in various fields.
Exploring Complex Numbers and Operations
Complex numbers extend our understanding of numbers beyond the real number system, allowing us to solve equations that cannot be addressed with real numbers alone. These numbers are essential in various fields such as electrical engineering, signal processing, and quantum physics. By understanding how to manipulate and operate with complex numbers, you gain powerful tools for solving a wide range of mathematical problems.
Structure of Complex Numbers

A complex number consists of two parts: a real part and an imaginary part. The real part is a traditional number, while the imaginary part is a multiple of the imaginary unit i, where i is defined as the square root of -1. The general form of a complex number is a + bi, where a is the real component and b is the coefficient of the imaginary part. Complex numbers can be added, subtracted, multiplied, and divided just like real numbers, with special rules for handling the imaginary unit i.
Operations with Complex Numbers
Operations involving complex numbers follow a similar structure to operations with real numbers, but with the inclusion of i. For addition and subtraction, combine like terms – the real parts with the real parts and the imaginary parts with the imaginary parts. When multiplying complex numbers, distribute each term in the binomial form, remembering that i² = -1. Division involves multiplying the numerator and denominator by the complex conjugate, which simplifies the expression into a form without an imaginary denominator.
Mastering complex numbers and their operations opens up a wide array of applications, from solving quadratic equations with no real solutions to analyzing oscillating systems in engineering. By applying the right techniques, you can efficiently solve problems that require these advanced mathematical tools.
Graphing Techniques for Functions and Equations
Graphing is a powerful visual tool that helps to represent mathematical relationships between variables. It provides insight into the behavior of different functions and equations, showing how values change and interact with one another. By mastering various graphing techniques, you can quickly analyze the characteristics of functions, determine their properties, and make informed decisions based on their graphs.
Plotting Basic Functions
To begin graphing, it is important to understand the basic shapes and behavior of different types of functions. For linear functions, the graph is a straight line, and for quadratic functions, it is a parabola. Knowing key points such as intercepts, vertices, and slopes will help you plot these functions accurately. For example, a linear function can be represented by the equation y = mx + b, where m is the slope and b is the y-intercept. By identifying these parameters, you can easily sketch the graph.
Transformations of Graphs
Transforming graphs involves shifting, stretching, compressing, and reflecting the basic shapes of functions. Horizontal and vertical shifts occur when the terms in the equation are adjusted. For instance, y = f(x – h) represents a horizontal shift by h units, while y = f(x) + k indicates a vertical shift by k units. Additionally, scaling and reflecting graphs help modify the appearance, allowing you to analyze more complex equations and their behaviors across different domains.
By practicing these techniques, you can develop a deeper understanding of how different functions behave graphically. This is particularly useful for solving problems, determining the solutions of equations, and interpreting data in a visual format.
Understanding Matrices and Determinants

Matrices are rectangular arrays of numbers or variables organized into rows and columns. They are fundamental tools in many areas of mathematics, particularly in systems of equations, transformations, and linear algebra. Understanding how to work with matrices allows you to solve complex problems efficiently, simplifying the process of organizing and manipulating data. Determinants, which are associated with square matrices, are used to evaluate the properties of a matrix, including its invertibility and the volume scaling factor in transformations.
Each matrix can represent a system of equations, where each row corresponds to one equation. The elements within the matrix provide the coefficients and constants for the equations. Operations on matrices, such as addition, subtraction, and multiplication, follow specific rules and are essential in solving linear systems or transforming geometric objects.
Determinants, which can only be computed for square matrices, provide key insights into the matrix’s characteristics. The determinant of a matrix is a scalar value that can be calculated from its elements, and it plays a crucial role in determining whether a matrix has an inverse. If the determinant is non-zero, the matrix is invertible; otherwise, it is singular, meaning it cannot be inverted.
By mastering matrix operations and understanding determinants, you gain powerful tools for solving systems of equations, performing linear transformations, and analyzing data in various mathematical contexts. These concepts are widely used in fields such as physics, economics, computer science, and engineering, where complex relationships are represented and solved using matrices and their properties.
Practice Problems for Success
To truly master the material and achieve success, practicing a variety of problems is essential. Working through different types of questions helps reinforce concepts, sharpen problem-solving skills, and build confidence. The more you practice, the more you become familiar with common patterns and strategies, which will be invaluable when tackling more complex challenges.
Key Areas to Focus On
- Linear Equations: Solve for unknowns, graph lines, and interpret slope and intercepts.
- Quadratic Functions: Practice factoring, completing the square, and solving using the quadratic formula.
- Systems of Equations: Solve by substitution, elimination, and graphical methods.
- Exponential Functions: Apply properties of exponents and logarithms in problem-solving scenarios.
- Polynomials: Perform addition, subtraction, multiplication, and division of polynomials.
- Rational Expressions: Simplify expressions, solve equations, and understand domain restrictions.
Example Problems
- Solve for x: 2x + 5 = 15
- Factor the quadratic expression: x² – 5x + 6
- Graph the system of equations: y = 2x + 3 and y = -x + 1
- Simplify: (3x² – 2x + 5) + (x² + 4x – 1)
- Solve the equation: 5(x – 2) = 3(x + 4)
Working through these and similar practice problems will ensure you are fully prepared to apply your knowledge to any situation. Be sure to check your solutions and understand the reasoning behind each step to reinforce learning and ensure lasting success.
Common Mistakes to Avoid During the Test
When faced with challenging problems, it’s easy to make mistakes that can cost valuable points. Being aware of common errors and knowing how to avoid them can significantly improve your performance. Many of these mistakes stem from simple oversights, misinterpretations, or rushing through the questions. By practicing careful reading and double-checking your work, you can minimize these errors and increase your chances of success.
1. Misreading the Question
One of the most common mistakes is not fully understanding what the question is asking. Always take a moment to carefully read each problem, paying attention to key words and instructions. Misinterpreting the problem can lead to incorrect approaches and answers.
2. Forgetting to Simplify
In many cases, it’s easy to stop after reaching an intermediate step, but failing to simplify your final expression or result can lead to an incomplete or incorrect answer. Always check if the problem requires simplification or if your final answer should be in its simplest form.
3. Not Double-Checking Work
Rushing through a test often leads to small calculation errors that could easily be avoided with a quick review. After solving a problem, take a moment to verify your work–check calculations, signs, and substitutions to ensure you haven’t missed anything.
4. Misusing Formulas
Make sure you are using the correct formulas for the right context. Confusing similar equations or applying them inappropriately can lead to errors. Be familiar with the formulas you need to know, but also understand when and why to use them.
5. Skipping Difficult Problems
It’s natural to feel stuck on tough questions, but skipping them without attempting to solve them can cost you points. Try to work through challenging problems step-by-step, and if you’re really stuck, mark them for review and move on to others–this might allow you to gain insight into the solution later on.
6. Not Managing Time Wisely
Improper time management can leave you with little time for the more difficult questions. Make sure to allocate your time efficiently: don’t spend too much time on one question and be mindful of how much time you have left for other sections.
By avoiding these common pitfalls and being mindful of your approach, you can navigate through the problems with greater confidence and accuracy. Take your time, stay focused, and remember that thoroughness and carefulness can make all the difference during the test.
How to Manage Time During the Test
Effective time management is crucial when taking a test that requires you to apply knowledge across various topics. Without proper planning, it’s easy to get caught up on difficult questions or spend too much time on one section, leaving little opportunity to complete others. By implementing strategies for managing your time wisely, you can ensure that you’re able to attempt all questions and maximize your performance.
1. Allocate Time for Each Section
Before diving into the test, quickly assess how many sections there are and how much time is available overall. Allocate time to each section based on its complexity and the number of questions it contains. This will give you a sense of how much time you should spend on each part of the test and help you stay on track.
2. Set Milestones and Stick to Them
As you work through the test, aim to complete each section within its allotted time. Setting mental milestones, such as completing a question every few minutes, can help you stay on pace. If you find yourself stuck on a question, move on to the next one and come back to it later, rather than wasting too much time trying to figure out one answer.
By using these strategies, you can ensure that you approach the test methodically, avoid unnecessary stress, and give yourself the best chance to complete everything on time.