
Support Vector Machines are a powerful tool in the world of machine learning, often used to tackle complex classification and regression tasks. Understanding the fundamental concepts behind these algorithms is essential for anyone looking to excel in this area. Mastery over their intricacies can lead to significant improvements in both practical applications and theoretical knowledge.
To succeed, it is crucial to focus on the key principles, including the role of hyperplanes, decision boundaries, and kernel functions. In addition, learning how to navigate common pitfalls and challenges is just as important. Proper preparation will allow you to confidently approach problems and solve them efficiently, making the most of the opportunities these techniques present.
In this section, we will delve into a variety of scenarios and techniques, designed to reinforce your understanding and boost your confidence. By practicing with carefully selected examples and exploring the underlying mechanisms, you will be able to tackle any challenge that comes your way.
SVM Exam Questions and Answers
When preparing for any assessment on machine learning algorithms, it’s essential to practice with a variety of problem types. This approach helps in understanding the core principles and improves the ability to apply them effectively in different scenarios. To achieve a high level of proficiency, it is important to familiarize oneself with different types of challenges that test theoretical knowledge as well as practical application skills.
Focusing on common problem formats, such as classification tasks, can enhance the ability to identify key features of data, understand the decision-making process, and implement solutions efficiently. In-depth practice with different examples will ensure a more complete grasp of the material, increasing both speed and accuracy during actual assessments.
Additionally, knowing how to approach complex tasks and recognizing potential pitfalls allows for more strategic problem-solving. By exploring a range of example cases and their solutions, it becomes easier to pinpoint areas that require further attention and improvement. The more diverse the problems, the stronger the foundation becomes, ensuring better results overall.
Overview of SVM in Machine Learning
In the field of machine learning, certain algorithms stand out for their ability to classify data effectively, even in complex, high-dimensional spaces. These models are used to create decision boundaries that separate distinct categories based on input features, making them invaluable for a wide range of tasks, from image recognition to predictive analytics. By understanding the core mechanisms behind these algorithms, one can harness their full potential in both academic and real-world applications.
Fundamental Concepts

At the heart of these algorithms lies the concept of creating optimal decision boundaries, or hyperplanes, that separate different classes of data. These boundaries are determined by maximizing the margin between the closest points of each class, known as support vectors. The greater the margin, the more confident the model is in its classification task, leading to better generalization to unseen data.
Applications in Various Fields
This technique has proven to be highly effective across numerous domains, including finance, healthcare, and natural language processing. By transforming input data into higher-dimensional spaces using kernel functions, these models can solve non-linear problems that other simpler algorithms struggle with. Whether it’s distinguishing between spam and non-spam emails or predicting stock market trends, the flexibility and power of this method make it a go-to choice for many machine learning practitioners.
Key Concepts to Understand for SVM
Mastering any machine learning model requires a deep understanding of its fundamental concepts. To excel in applying this technique, it’s crucial to grasp several core principles that govern its functionality. These concepts form the foundation of how the model interprets data and makes decisions, impacting both its accuracy and efficiency in real-world tasks.
- Hyperplane: The decision boundary that separates different classes of data. Its position is key to ensuring the model can accurately classify new data.
- Support Vectors: The data points that are closest to the hyperplane. These points are critical in determining the optimal margin.
- Margin: The distance between the hyperplane and the nearest data points from each class. Maximizing the margin leads to a more robust model.
- Kernel Function: A technique used to transform input data into higher-dimensional spaces, making it easier to classify non-linear relationships.
- Regularization: A parameter that helps prevent overfitting by controlling the trade-off between achieving a perfect separation and maintaining generalization ability.
By mastering these concepts, one can better understand how the model works, troubleshoot potential issues, and apply the technique more effectively to various types of data.
Common SVM Algorithms Explained
Various algorithms are used to build models that can efficiently classify data into distinct categories. These algorithms are designed to handle different types of data and challenges, from linear separability to more complex, non-linear problems. Understanding how each algorithm works and when to apply them is essential for achieving optimal performance in real-world tasks.
Linear Classifier
The linear classifier is one of the simplest and most widely used methods. It works well when the data is linearly separable, meaning that a straight line or hyperplane can be used to separate the different classes. This method aims to find the hyperplane that maximizes the margin between the classes, providing a robust solution for binary classification tasks.
Non-Linear Classifier with Kernels

In cases where data cannot be separated by a straight line, kernel functions come into play. By transforming the input data into a higher-dimensional space, these algorithms can create more complex decision boundaries that handle non-linear relationships. Common kernel functions include the polynomial kernel and the radial basis function (RBF) kernel. These allow the algorithm to capture intricate patterns in the data that would otherwise be difficult to detect.
Choosing the Right Algorithm depends on the nature of the data. For simple tasks with clear separations, a linear model may suffice, while more complex problems may require the use of kernel functions to handle non-linearity and improve classification performance.
How to Approach SVM Exam Questions
When faced with challenges that assess your understanding of machine learning models, having a systematic approach is crucial for success. By breaking down problems into manageable steps, you can more effectively identify key elements and devise solutions. This approach ensures that you tackle each part of the problem methodically, reducing errors and boosting confidence.
Understand the Problem Context
The first step is to thoroughly read the problem statement. Often, tasks will involve classifying data or determining the best way to separate two categories. Take time to identify the type of data you are working with (linear vs. non-linear) and the method that might best solve the problem. This helps in determining whether you need to use basic techniques or more advanced tools like kernel functions.
Break the Problem into Components
Once you’ve identified the key points of the problem, break it down into smaller sections. Start by focusing on the fundamental aspects, such as the input features and the target classes. Determine if the model should focus on maximizing margins or minimizing classification errors. By handling one aspect at a time, you can ensure that your approach remains clear and organized.
Practice and repetition are key to mastering this approach. The more you practice with different problem types, the quicker you will become at recognizing patterns and applying the right techniques efficiently.
Typical SVM Exam Question Formats

In assessments related to machine learning models, the format of the problems often varies, but certain structures are commonly seen. These types of questions are designed to test not only your theoretical knowledge but also your ability to apply concepts in practical scenarios. Understanding the most frequent formats will help you approach each problem with confidence and clarity.
Common Problem Types
- Conceptual Questions: These questions assess your understanding of key principles, such as the role of support vectors or the importance of kernel functions. They typically ask for definitions or explanations of specific terms.
- Mathematical Problems: These often involve deriving formulas, solving equations, or demonstrating how the model finds the optimal decision boundary based on given data points.
- Scenario-Based Questions: These problems present a real-world scenario where you must choose the most appropriate method, such as deciding between different kernel functions for a given dataset.
Practical Application Questions

- Model Performance Evaluation: These questions might ask you to analyze the performance of a model, interpret results from a confusion matrix, or assess accuracy and precision.
- Data Preprocessing Tasks: You may be asked how to prepare data for model training, including scaling features or handling missing values.
- Implementation Challenges: Some problems require you to apply knowledge by writing code or explaining steps to implement a specific model.
By practicing these formats, you can ensure a more organized and efficient approach when addressing problems, whether theoretical or applied.
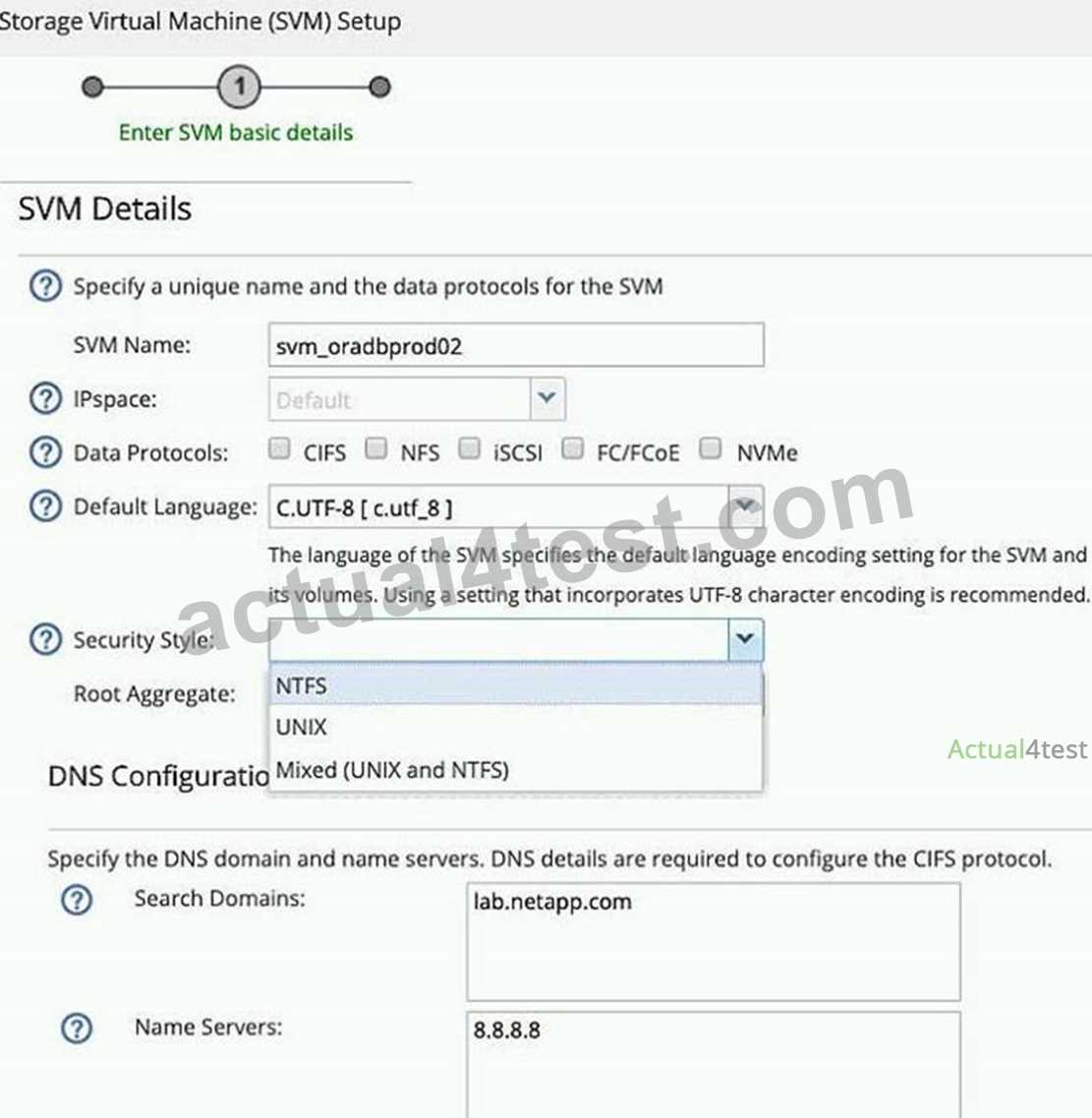
Understanding Support Vectors and Hyperplanes
In machine learning, the ability to separate data into distinct classes is fundamental to building an effective model. Key to this process are the concepts of decision boundaries and the critical data points that influence their placement. By understanding these components, you gain insight into how the model operates and how it can be optimized for better performance.
Support Vectors
Support vectors are the data points that lie closest to the decision boundary. These points play a crucial role in determining the optimal position of the boundary, as they directly affect the model’s accuracy. By maximizing the margin between the support vectors of different classes, the model ensures that new, unseen data will be classified correctly. Essentially, support vectors are the backbone of the model, as they provide the most informative points for training.
Hyperplanes
A hyperplane is a decision boundary that separates data into different categories. In two-dimensional space, it’s simply a line, but in higher dimensions, it becomes a plane or hyperplane. The position of the hyperplane is crucial for the accuracy of the model. The goal is to place the hyperplane such that it maximizes the margin between the two classes, ensuring that the classification is as reliable as possible. The hyperplane is determined by the support vectors, which are the closest points to it, making them essential in constructing an optimal model.
Role of Kernel Functions in SVM
In many real-world problems, the data is not linearly separable, making it difficult to apply simple linear models. To overcome this, kernel functions are used to transform data into higher-dimensional spaces, where a linear separation becomes possible. This transformation enables the model to handle complex relationships in the data, making it more versatile and powerful.
How Kernel Functions Work
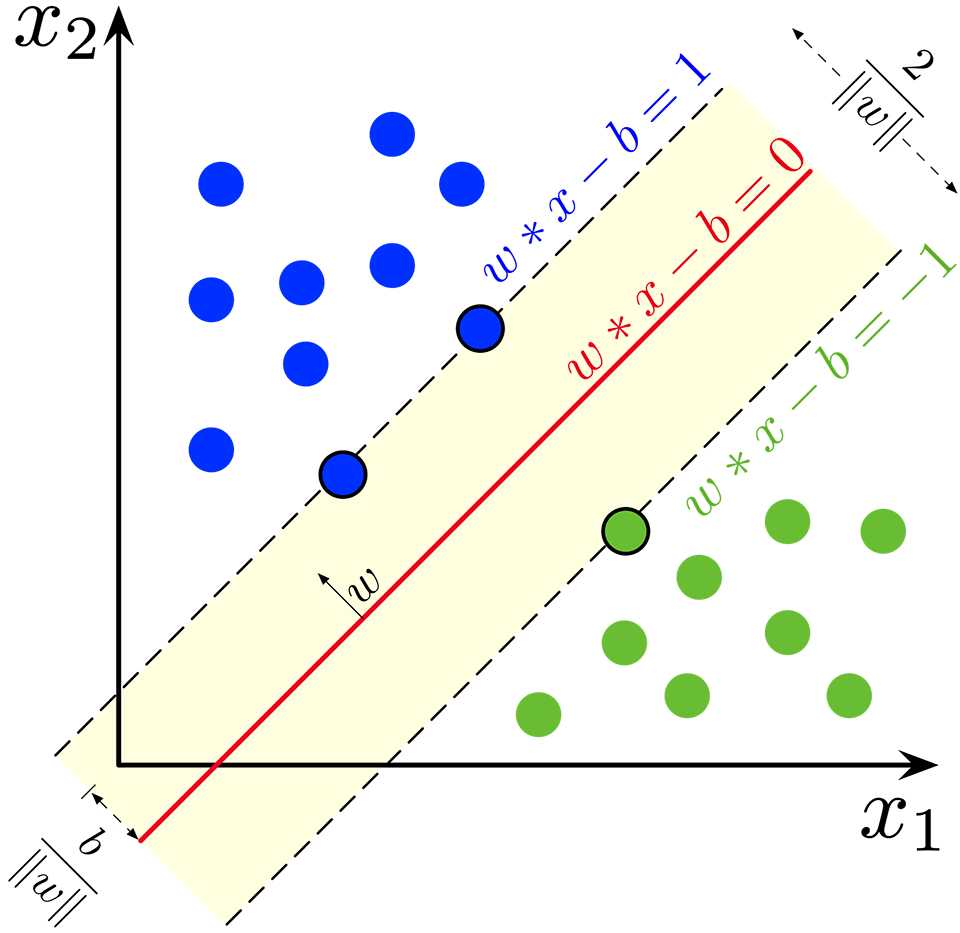
Kernel functions allow a model to operate in a higher-dimensional space without the need to explicitly calculate the coordinates in that space. This is known as the “kernel trick.” By mapping the data to a higher-dimensional space, the kernel function makes it easier to find an optimal separating hyperplane, even in cases where the original data is not linearly separable. Common kernel functions include the polynomial kernel, which creates polynomial decision boundaries, and the radial basis function (RBF) kernel, which is highly effective in capturing non-linear relationships.
Choosing the Right Kernel
Choosing the appropriate kernel is crucial for model performance. If the data is close to being linearly separable, a linear kernel may be sufficient. However, for more complex datasets, a non-linear kernel, such as the RBF kernel, may provide better results. The right kernel can significantly improve the model’s ability to generalize and make accurate predictions, making it essential to understand the underlying structure of the data before selecting the kernel.
Choosing the Right Kernel for SVM
One of the key factors that influence the performance of a machine learning model is the choice of kernel. The kernel function defines how the model interprets the data and determines the decision boundary. Selecting the appropriate kernel is crucial for ensuring that the model can effectively classify data, especially when the data is complex or not linearly separable.
Common Kernels and Their Uses
- Linear Kernel: Best suited for data that is linearly separable. This kernel is simple and computationally efficient, making it a good choice for tasks where a straight line or hyperplane can easily separate the classes.
- Polynomial Kernel: Useful for data that requires polynomial decision boundaries. It can handle higher-order relationships between data points, making it ideal for moderately complex datasets.
- Radial Basis Function (RBF) Kernel: One of the most commonly used kernels, it works well for data that has complex, non-linear relationships. The RBF kernel can map the data into an infinite-dimensional space, allowing the model to capture intricate patterns and provide more accurate predictions.
- Sigmoid Kernel: Similar to the activation function in neural networks, the sigmoid kernel is useful for tasks that resemble classification problems in neural networks. It is less commonly used but can be effective for certain types of datasets.
Factors to Consider When Choosing a Kernel
When selecting a kernel, several factors should be considered:
- Data Distribution: If the data is linearly separable, a linear kernel is often sufficient. For more complex data, non-linear kernels like RBF or polynomial are better choices.
- Computation Efficiency: Some kernels, especially RBF, can be computationally expensive. If processing speed is critical, consider the trade-off between model accuracy and computational cost.
- Model Overfitting: While more complex kernels like RBF can provide better accuracy, they may also lead to overfitting. Regularization techniques can help mitigate this risk.
By carefully analyzing the characteristics of your dataset and understanding the strengths and limitations of each kernel, you can select the best option to enhance the model’s performance.
Common Mistakes in SVM Exams
When working with machine learning models, it’s easy to make errors that could lead to incorrect conclusions or suboptimal model performance. These mistakes often stem from misunderstandings of key concepts, misinterpretations of the problem, or even simple computational oversights. Identifying these common pitfalls can help you avoid them and improve your understanding of how to effectively apply these models.
Common Pitfalls
- Ignoring Data Preprocessing: Failing to properly scale or normalize the data can severely impact model performance. This is especially true when using kernel functions, where feature scaling plays a key role in ensuring that the model works as intended.
- Overfitting by Using Complex Kernels: While non-linear kernels like RBF can capture complex patterns, they may also lead to overfitting, especially with smaller datasets. Choosing a more complex kernel without considering the risk of overfitting can result in poor generalization.
- Misunderstanding the Role of Support Vectors: Support vectors are the critical data points that influence the decision boundary. Ignoring or misinterpreting their importance can lead to suboptimal models, especially when working with small or imbalanced datasets.
- Improper Selection of Hyperparameters: Incorrectly tuning parameters, such as the regularization parameter (C) or kernel-specific parameters (like gamma for the RBF kernel), can result in either overfitting or underfitting. Always ensure hyperparameters are tuned carefully to find the right balance.
- Relying on Default Settings: Using default settings without considering the specific characteristics of the dataset can lead to poor results. It’s essential to experiment with different parameters and kernels to find the most suitable configuration for each problem.
How to Avoid These Mistakes
- Thoroughly Preprocess Data: Ensure that all features are properly scaled and cleaned before training the model. This step is crucial for ensuring the model works optimally.
- Choose the Right Complexity: Always consider the complexity of the problem before choosing a kernel. For simple datasets, a linear model may be sufficient, while more complex data might require non-linear kernels with careful regularization.
- Focus on Key Data Points: Pay close attention to support vectors, as they directly influence the decision boundary. Properly identifying these points can significantly improve the model’s accuracy.
- Experiment with Hyperparameters: Avoid relying on default settings. Test different configurations and tune parameters to achieve the best model performance.
By being mindful of these common mistakes, you can approach problems more strategically, leading to more accurate models and better results in machine learning tasks.
How to Solve SVM Classification Problems
Solving classification problems involves transforming data into a format that a machine learning model can use to effectively distinguish between different categories. The process typically includes several key steps, from data preprocessing to selecting an appropriate model and tuning it for optimal performance. Understanding the overall flow of solving classification tasks is essential for building accurate and efficient models.
Here is a step-by-step guide on how to approach classification challenges:
| Step | Description |
|---|---|
| 1. Data Collection | Gather and organize the dataset for analysis. Ensure that data is representative of the problem you’re trying to solve and includes all relevant features. |
| 2. Data Preprocessing | Clean the data by handling missing values, removing outliers, and normalizing or scaling the features. This step is crucial for improving the accuracy of the model. |
| 3. Choosing the Model | Select a model based on the complexity of the data. Linear models are suitable for simpler datasets, while non-linear kernels might be required for more complex problems. |
| 4. Hyperparameter Tuning | Fine-tune the hyperparameters of the model, such as the regularization parameter (C) and kernel-specific parameters, to find the best configuration. |
| 5. Model Training | Train the model on the prepared dataset. Ensure that the training process involves cross-validation to avoid overfitting and ensure generalization. |
| 6. Evaluation | Evaluate the model’s performance using relevant metrics, such as accuracy, precision, recall, and F1-score. Analyze the confusion matrix to identify areas for improvement. |
| 7. Model Optimization | Optimize the model by experimenting with different kernels, adjusting regularization parameters, or using feature engineering techniques to improve performance. |
| 8. Testing | Test the model on unseen data to verify its generalization capabilities. Make necessary adjustments based on the results before final deployment. |
By following these steps, you can effectively address classification challenges and build a model that performs accurately across a wide range of tasks. Each step plays a critical role in ensuring that the model not only fits the training data well but also generalizes effectively to new, unseen examples.
Effect of Regularization in SVM
Regularization is a technique used in machine learning models to prevent overfitting by controlling the complexity of the model. In classification tasks, it plays a crucial role in balancing the trade-off between achieving a low error on the training set and ensuring that the model generalizes well to unseen data. By adjusting regularization parameters, you can influence the margin between classes and control how flexible the decision boundary is.
Understanding Regularization
In the context of classification, regularization helps manage the model’s bias-variance trade-off. When a model is too complex, it tends to fit the noise in the training data, resulting in overfitting. On the other hand, if the model is too simple, it may underfit the data and fail to capture important patterns. Regularization introduces a penalty for complexity, which encourages the model to be simpler and more generalizable.
Impact of Regularization Parameter (C)
- High Regularization (Large C): When the regularization parameter is large, the model becomes more sensitive to the training data. It will focus on minimizing classification errors, which may lead to a more complex decision boundary. This can increase the risk of overfitting, especially if the data is noisy or not representative of the broader distribution.
- Low Regularization (Small C): A smaller regularization parameter allows the model to tolerate more errors on the training data, resulting in a simpler decision boundary. This approach may help reduce overfitting but can also increase the risk of underfitting if the model fails to capture important patterns in the data.
By carefully selecting the right value for the regularization parameter, you can control the model’s complexity and its ability to generalize effectively to new data. Regularization thus plays a key role in ensuring that the model performs well not just on the training set but also on unseen data.
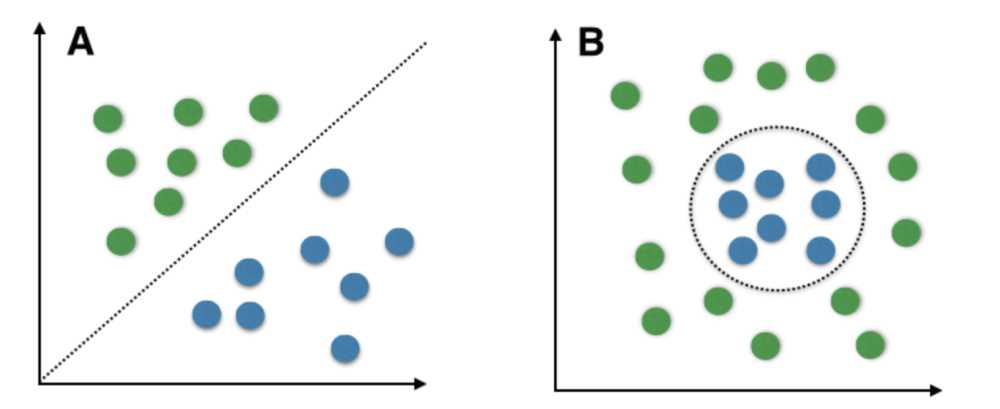
SVM for Nonlinear Data Classification
When dealing with complex datasets where the classes are not linearly separable, traditional linear classifiers may fail to provide accurate results. To address this issue, techniques that can handle non-linear decision boundaries are necessary. One such approach leverages mathematical functions to map data into higher-dimensional spaces where a linear separator can be found. This enables the model to capture intricate patterns and improve classification performance for nonlinear data.
Nonlinear Decision Boundaries
In cases where the relationship between the features and the target class is not linear, a simple straight line or hyperplane will not suffice. In these situations, a transformation is applied to map the data into a higher-dimensional space, where a linear separator can be found. This transformation makes it possible to classify the data with a decision boundary that would be impossible to achieve in the original space.
Using Kernel Functions for Nonlinear Classification
Kernel functions are crucial in transforming data for nonlinear classification tasks. They map the input features into higher dimensions without the need for explicitly calculating the transformation. This allows models to find non-linear decision boundaries in the transformed space, which would be challenging to identify in the original feature space.
- Polynomial Kernel: Useful when data exhibits polynomial relationships between features. It can capture more complex decision boundaries than a linear model.
- Radial Basis Function (RBF) Kernel: One of the most popular kernels for nonlinear classification, it allows for highly flexible decision boundaries and is effective in capturing complex patterns in data.
- Sigmoid Kernel: Often used when the problem is similar to a neural network classification task, the sigmoid kernel introduces a non-linear transformation that can separate complex data.
By selecting the appropriate kernel and tuning the model parameters, it’s possible to build classifiers that perform well even in the face of highly complex, nonlinear datasets. This ability to adapt to the underlying structure of the data is key to improving prediction accuracy and achieving better generalization across different types of problems.
Evaluating Model Performance in SVM
Assessing the performance of a machine learning model is essential to ensure it effectively solves the problem at hand. For classification models, performance evaluation involves determining how well the model can predict new, unseen data. This is done by calculating various metrics that provide insights into the model’s accuracy, reliability, and ability to generalize. Understanding these metrics and how to interpret them is key to improving model performance.
Below is a table of common evaluation metrics used to assess classification models:
| Metric | Description |
|---|---|
| Accuracy | The proportion of correct predictions to the total number of predictions. A high accuracy indicates that the model is performing well on the dataset, but it may not always be enough for imbalanced data. |
| Precision | Measures the accuracy of positive predictions. It is the ratio of true positive predictions to the total predicted positives. High precision means that when the model predicts a positive class, it is often correct. |
| Recall | Also known as sensitivity, recall measures the model’s ability to identify all relevant instances. It is the ratio of true positives to the total actual positives. High recall means that the model successfully identifies most of the positive instances. |
| F1-Score | A harmonic mean of precision and recall, providing a single metric that balances both aspects. It is particularly useful when there is an uneven class distribution. |
| Confusion Matrix | A table that displays the true positives, false positives, true negatives, and false negatives, allowing you to visually assess where the model is making errors. |
| ROC Curve | Used to evaluate the trade-off between true positive rate and false positive rate. The area under the ROC curve (AUC) is a valuable measure of the model’s overall performance. |
By analyzing these metrics, you can gain a comprehensive understanding of how well your model is performing. Depending on the task at hand, different metrics may be more important. For example, in cases of imbalanced datasets, precision and recall may offer more valuable insights than accuracy alone. By evaluating the performance from multiple angles, you can fine-tune the model to achieve optimal results.
Practice Questions for SVM Exams

Preparing for any assessment related to machine learning requires an understanding of the core concepts and techniques. Practicing through various hypothetical scenarios and problem-solving exercises is a vital part of the preparation process. By working through different types of problems, you can test your knowledge, identify areas for improvement, and gain the confidence needed for success. Below are some practice exercises that will help reinforce the key principles of classification models.
Sample Problems
Here are several practice problems designed to test your understanding of fundamental concepts and techniques related to model training and evaluation:
| Problem | Solution |
|---|---|
| Given a set of data points, how would you determine if the data is linearly separable or not? | To check for linear separability, plot the data and visually inspect the distribution. If no straight line can divide the points into distinct categories, the data is non-linearly separable. Alternatively, you could apply a transformation to a higher dimension to test for separability. |
| What is the role of a kernel function when dealing with nonlinear data? | A kernel function maps the data into a higher-dimensional space where a linear separator can be found. By doing this, the model can classify data that is not linearly separable in its original form, without explicitly computing the transformation. |
| Explain the difference between precision and recall, and when would you prioritize one over the other? | Precision refers to the accuracy of positive predictions, while recall measures the ability to correctly identify all positive instances. In cases where false positives are costly (e.g., email spam filtering), precision is more important. However, when false negatives are more critical (e.g., medical diagnoses), recall should be prioritized. |
| How would you adjust a model if you notice that it is overfitting the training data? | If a model is overfitting, consider increasing regularization, reducing the model complexity, or using more training data. Another approach is to implement cross-validation to ensure the model generalizes better to unseen data. |
Key Concepts to Review
It’s crucial to revisit specific topics before taking any assessment. Focus on understanding these areas deeply:
- How different kernel functions (e.g., polynomial, RBF) affect the model’s performance
- The importance of regularization in controlling model complexity
- The interpretation of metrics like precision, recall, F1-score, and accuracy
- Common strategies for handling imbalanced datasets
By working through these practice scenarios and reviewing the essential concepts, you’ll be better prepared to tackle any challenges you may encounter in assessments or real-world applications.
Tips for SVM Exam Success
Achieving success in assessments related to machine learning requires a combination of strategy, knowledge, and practice. A solid understanding of key concepts is vital, but effective preparation also involves honing your problem-solving skills, staying organized, and managing your time wisely. The following tips can help ensure that you’re fully prepared and confident on test day.
Understand the Core Concepts
Make sure you have a clear understanding of the fundamental concepts involved in model training, such as regularization, kernel functions, and model evaluation metrics. Being able to explain these concepts in simple terms will make it easier to apply them to different types of problems.
Practice with Realistic Scenarios
One of the best ways to prepare is to work through practice problems that mimic the kinds of tasks you might face in an assessment. This helps you become comfortable with problem-solving under time constraints. Try to focus on various scenarios, from basic classification tasks to more complex, nonlinear datasets.
Focus on Problem-Solving Techniques
When solving problems, make sure to break them down into smaller, manageable steps. Start by identifying the core components of the task, such as the features, target variable, and data distribution. Next, consider which model parameters and techniques are most appropriate for the task, and think about the most efficient way to compute and validate your solution.
Master Key Evaluation Metrics
Learn how to interpret evaluation metrics like accuracy, precision, recall, and the confusion matrix. Knowing when and why to use each metric will help you assess your model’s performance and avoid overfitting or underfitting.
Time Management
During an assessment, time can quickly become a limiting factor. Practice managing your time effectively by setting time limits for each question during your practice sessions. This helps ensure that you can tackle all the problems within the given timeframe without rushing.
Stay Calm and Focused
On the day of the assessment, it’s important to stay calm and focused. Take a deep breath before starting, and approach each problem systematically. If you get stuck on a particular question, move on and come back to it later with a fresh perspective.
By following these tips and staying disciplined in your study routine, you can approach any challenge with confidence and improve your chances of success.