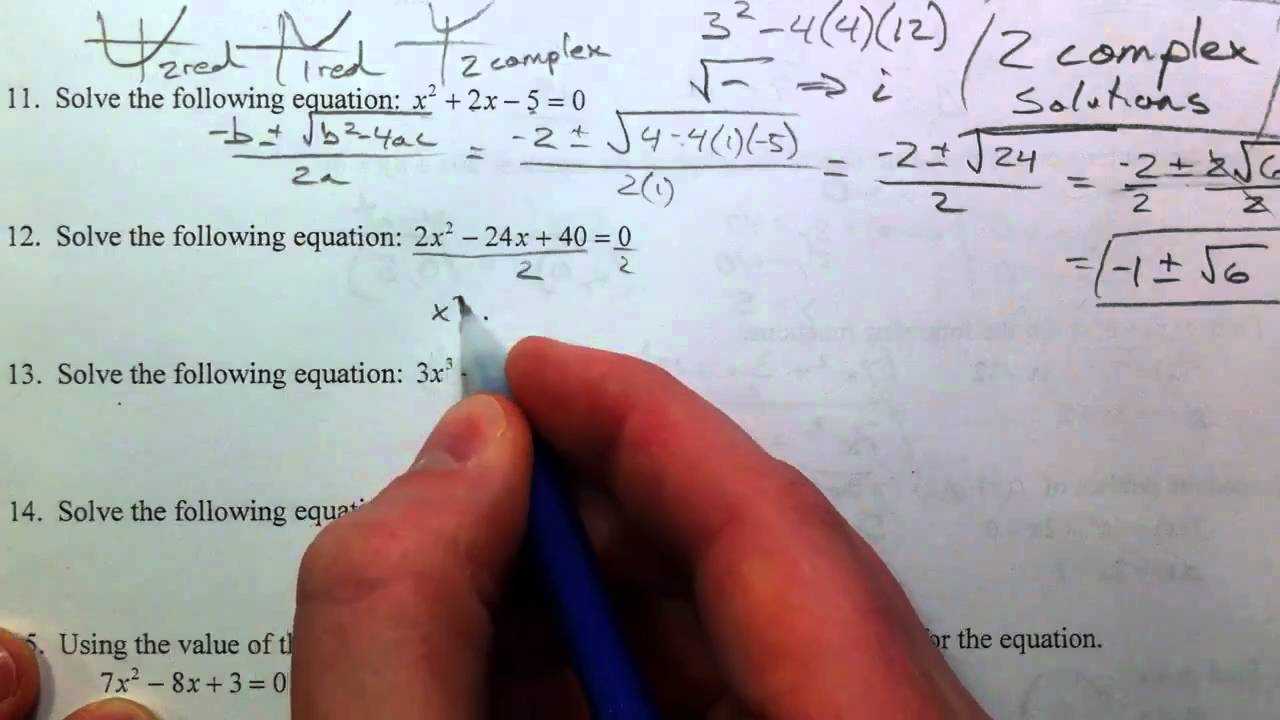
The final stages of any mathematics course often require a deep understanding of key principles, as well as the ability to apply them to complex problems. This section is designed to help consolidate your knowledge and prepare for a comprehensive evaluation of your skills. Whether you’re reviewing techniques for solving equations or exploring advanced problem-solving strategies, this guide will serve as a valuable resource.
As you approach the end of your studies, it’s crucial to focus on the major topics covered throughout the course. Mastery of these concepts is essential not only for academic success but also for building a solid foundation for future mathematical challenges. With a clear understanding of core topics, you’ll be well-prepared to tackle any questions that arise.
Preparation is key in these final moments. By reviewing critical areas like functions, graphing, and solving complex expressions, you ensure that you have the tools needed to succeed. Remember that consistent practice and a focus on the areas where you feel less confident will go a long way in boosting your performance.
Mathematical Concepts for Final Assessment
Mastering the essential topics covered during your studies is critical as you approach the final phase. This section aims to provide clarity on key areas, ensuring you’re ready for a comprehensive evaluation. From understanding advanced equations to analyzing different types of functions, each concept plays a crucial role in achieving success. Focused practice and in-depth exploration of these topics will give you the confidence needed to perform well.
Key Topics to Focus On
- Solving Complex Equations: Understand how to manipulate and solve equations involving multiple variables and operations.
- Graphing Functions: Be able to interpret and plot various functions, including linear, quadratic, and exponential.
- Rational Expressions: Practice simplifying and solving equations that involve fractions with polynomials in both the numerator and denominator.
- Logarithmic and Exponential Forms: Familiarize yourself with the relationship between logarithms and exponents, and practice converting between the two.
- Systems of Equations: Work on solving systems using different methods such as substitution, elimination, and matrices.
Common Mistakes to Avoid
- Failing to properly factor expressions, which can lead to incorrect solutions.
- Misinterpreting function graphs, especially when identifying key characteristics like intercepts and asymptotes.
- Overlooking negative signs during simplification and solving processes.
- Confusing the properties of exponents when working with powers and radicals.
- Skipping steps when solving for variables, which can lead to errors in intermediate calculations.
By focusing on these core areas and recognizing common pitfalls, you’ll be well-prepared to approach any question confidently. Remember, consistent practice and review are the best tools for success in your upcoming evaluation.
Key Concepts to Review
In order to excel in any final assessment, it’s essential to revisit the fundamental principles that form the basis of your studies. Understanding the core topics will not only reinforce your problem-solving abilities but also ensure you’re prepared for complex challenges. This section highlights the critical concepts you should focus on to strengthen your foundation and enhance your readiness.
Equations and Inequalities are key areas to revisit. Being able to manipulate and solve equations, whether linear, quadratic, or higher-order, is crucial. Pay particular attention to how to handle both equality and inequality relationships, as they often present similar but distinct challenges.
Functions and Their Properties should also be reviewed carefully. Whether you’re working with linear, exponential, or logarithmic functions, understanding how these equations behave and how to graph them is vital. Look at the different transformations that can occur, such as shifting, stretching, and reflecting.
Systems of Equations are another important concept. Be comfortable with solving systems of linear equations using methods like substitution and elimination, and don’t forget the application of matrices in more complex systems. Practice solving word problems that require system-solving techniques.
Advanced Factoring will also appear frequently. Revising different factoring techniques–like factoring by grouping, using the difference of squares, and factoring trinomials–will help you tackle more challenging problems that involve higher-degree polynomials.
Radicals and Rational Expressions should not be overlooked. These types of expressions require special attention, particularly when simplifying or solving equations that involve roots and fractions with polynomials. Ensure you understand how to simplify and rationalize denominators effectively.
Understanding Quadratic Equations
Quadratic equations are one of the most fundamental topics in mathematics. They are equations where the highest exponent of the variable is 2, and they often arise in a wide range of real-world applications, from physics to finance. Solving these equations is essential for mastering various mathematical techniques and for developing a deeper understanding of how variables interact in different contexts.
To solve a quadratic equation, the most common method is factoring, but other techniques, such as completing the square and using the quadratic formula, are also crucial. Each of these methods offers a unique approach to finding the values of the variable that satisfy the equation. Recognizing the structure of a quadratic equation can help you determine the best method to use for a given problem.
Factoring is often the quickest way to solve a quadratic equation when the equation is easily factorable. By expressing the equation as a product of two binomials, you can find the solutions by setting each factor equal to zero.
Completing the square is another powerful technique, especially when the equation is not easily factorable. This method involves manipulating the equation to create a perfect square trinomial, which can then be solved by taking square roots.
The quadratic formula is a universal method that can be applied to any quadratic equation. This formula, x = (-b ± √(b² – 4ac)) / 2a, provides the solutions directly by plugging in the coefficients from the equation.
Understanding the graph of a quadratic equation is equally important. The graph of any quadratic equation is a parabola, and knowing how to find its vertex, axis of symmetry, and intercepts can help in visualizing and solving the equation more effectively.
Rational Expressions Simplified
Rational expressions, which are fractions involving polynomials, require careful handling to simplify. Simplifying these expressions is essential for solving equations and performing various operations. The goal is to rewrite the expression in a more manageable form, making it easier to work with in larger problems or calculations.
The first step in simplifying rational expressions is factoring both the numerator and the denominator. By factoring out common factors, you can cancel out terms that appear in both the numerator and the denominator. This often leads to a much simpler expression that is easier to work with.
Identifying common factors is key to simplifying rational expressions. Look for terms that appear in both the top and bottom, and factor them out wherever possible. For example, in an expression like (x² – 4) / (x + 2), you can factor the numerator as (x – 2)(x + 2), allowing the (x + 2) terms to cancel out.
Reducing to lowest terms is another crucial step. After canceling out common factors, ensure that no further simplifications can be made. It’s important to check that the expression cannot be reduced further, and any remaining terms are in their simplest form.
In some cases, you may need to perform additional operations such as multiplying or dividing rational expressions. When multiplying, multiply the numerators and denominators separately and then simplify. When dividing, multiply by the reciprocal of the second expression.
Remember, the key to success with rational expressions is practice and attention to detail. Mastering the techniques of factoring and simplifying will make it easier to handle more complex problems as you move forward in your studies.
Solving Polynomial Equations
Solving polynomial equations involves finding the values of the variable that make the equation true. These equations can range from simple quadratics to higher-degree polynomials, and the methods used to solve them can vary depending on the complexity of the equation. Understanding the techniques for solving polynomial equations is essential for tackling more advanced mathematical problems.
One of the first methods to apply is factoring. When a polynomial can be factored into simpler binomials or trinomials, you can set each factor equal to zero and solve for the variable. For example, the equation x² – 5x + 6 = 0 can be factored as (x – 2)(x – 3) = 0, leading to the solutions x = 2 and x = 3.
If factoring is not possible, synthetic division or long division can be used to break down the polynomial into smaller, more manageable parts. These techniques are especially useful when dealing with polynomials of degree greater than two, where factoring becomes less straightforward.
The quadratic formula is another powerful tool when dealing with second-degree polynomials. If a polynomial cannot be easily factored, the quadratic formula x = (-b ± √(b² – 4ac)) / 2a can provide the solutions directly by substituting the coefficients from the equation.
For higher-degree polynomials, graphing can also help find solutions. By plotting the polynomial function, you can identify where the graph intersects the x-axis, which corresponds to the real roots of the equation.
When solving polynomial equations, it’s important to remember that some equations may have complex or imaginary solutions. If the discriminant (the part of the quadratic formula under the square root) is negative, the equation will have complex solutions, which require further knowledge of complex numbers to fully understand.
Exponential and Logarithmic Functions
Exponential and logarithmic functions are closely related, and mastering them is essential for solving a wide range of problems in mathematics. These functions often appear in real-life applications such as population growth, financial calculations, and scientific data analysis. Understanding how to work with both functions will enable you to solve equations involving exponents and logarithms with ease.
Exponential functions involve expressions where a constant base is raised to a variable exponent. The general form is f(x) = a * b^x, where a is a constant, b is the base, and x is the exponent. These functions model rapid growth or decay, depending on whether the base is greater than 1 or between 0 and 1.
Logarithmic functions are the inverse of exponential functions. They are used to solve equations where the unknown appears as the exponent. The general form is f(x) = log_b(x), where b is the base and x is the argument. A key property of logarithms is that they transform multiplication into addition, division into subtraction, and exponentiation into multiplication.
Key Properties and Rules
- Inverse Relationship: Logarithms undo the effect of exponentiation. For example, log_b(b^x) = x.
- Product Rule: log_b(x * y) = log_b(x) + log_b(y).
- Quotient Rule: log_b(x / y) = log_b(x) – log_b(y).
- Power Rule: log_b(x^n) = n * log_b(x).
- Change of Base Formula: log_b(x) = log_c(x) / log_c(b), which allows you to calculate logarithms with different bases.
Solving Exponential and Logarithmic Equations
- For exponential equations like b^x = y, take the logarithm of both sides to solve for x.
- For logarithmic equations like log_b(x) = y, rewrite the equation in exponential form: b^y = x.
- Use properties of logarithms to simplify expressions before solving for the variable.
Both types of functions have distinct applications and offer a variety of techniques for solving equations. Mastering the concepts of exponential growth and decay, as well as the manipulation of logarithmic expressions, will significantly improve your problem-solving skills and mathematical understanding.
Systems of Linear Equations
Systems of linear equations involve multiple equations with multiple variables, and solving these systems requires finding the values of the variables that satisfy all the equations simultaneously. These types of problems appear frequently in real-world scenarios, such as in economics, physics, and engineering, where multiple conditions must be met at once. There are several methods to solve such systems, each suited to different types of equations and situations.
Three common methods for solving systems of linear equations are:
- Substitution method: Solve one equation for one variable and substitute this expression into the other equation.
- Elimination method: Add or subtract equations to eliminate one variable, making it easier to solve for the remaining variable.
- Graphical method: Plot both equations on a graph, where the solution corresponds to the point where the two lines intersect.
Example of a System of Linear Equations
Consider the following system:
| Equation 1 | 2x + 3y = 12 |
| Equation 2 | 4x – y = 5 |
To solve this system, you can use the substitution or elimination method. For instance, by solving Equation 2 for y, we get:
4x – y = 5 → y = 4x – 5
Now, substitute this expression for y into Equation 1:
2x + 3(4x – 5) = 12
Expand and simplify to find the value of x:
2x + 12x – 15 = 12 → 14x = 27 → x = 27/14
Substitute this value of x back into the expression for y:
y = 4(27/14) – 5 = 108/14 – 5 = 108/14 – 70/14 = 38/14 = 19/7
Thus, the solution to the system is x = 27/14 and y = 19/7.
Understanding how to solve systems of equations is crucial for tackling complex problems involving multiple variables. Depending on the situation, one method may be more efficient than the others, but all methods ultimately lead to the same solution if applied correctly.
Conic Sections and Their Properties
Conic sections are curves formed by the intersection of a plane and a cone. These curves have distinct properties and play a crucial role in various fields of study, from geometry to physics. The four primary types of conic sections–circles, ellipses, parabolas, and hyperbolas–each have unique characteristics and equations that govern their shapes and behaviors. Understanding these properties is essential for solving problems involving these curves in both theoretical and applied contexts.
Types of Conic Sections
- Circle: A circle is a set of points equidistant from a central point. Its equation in standard form is (x – h)² + (y – k)² = r², where (h, k) is the center, and r is the radius.
- Ellipse: An ellipse is a set of points such that the sum of the distances from any point on the curve to two fixed points (foci) is constant. Its equation is ((x – h)² / a²) + ((y – k)² / b²) = 1, where a is the length of the major axis and b is the length of the minor axis.
- Parabola: A parabola is a set of points equidistant from a point (focus) and a line (directrix). Its equation is y = ax² + bx + c, or in vertex form y = a(x – h)² + k, where (h, k) is the vertex of the parabola.
- Hyperbola: A hyperbola is a set of points where the difference in distances to two fixed points (foci) is constant. Its equation is ((x – h)² / a²) – ((y – k)² / b²) = 1, where a and b are constants related to the shape of the hyperbola.
Key Properties of Conic Sections
- Symmetry: Conic sections are often symmetric. Circles and ellipses have rotational symmetry, while parabolas and hyperbolas have reflective symmetry.
- Focus and Directrix: The concept of the focus and directrix is essential for parabolas, ellipses, and hyperbolas. These elements help define the shape and location of the curve.
- Asymptotes: Hyperbolas have asymptotes, which are lines that the curve approaches but never intersects. These lines provide insight into the behavior of the hyperbola at large distances from the center.
- Vertex: The vertex is a key point in parabolas and ellipses, representing the maximum or minimum point for parabolas, and the extreme points on the major and minor axes for ellipses.
By analyzing the equations and properties of conic sections, one can solve a wide range of geometric problems. Whether you are dealing with the trajectory of projectiles or the orbits of planets, a deep understanding of these curves and their characteristics is fundamental in various branches of mathematics and science.
Working with Matrices and Determinants

Matrices are rectangular arrays of numbers, symbols, or expressions arranged in rows and columns, and they provide a powerful tool for solving systems of linear equations, transforming geometric shapes, and representing complex data. The determinant, a scalar value computed from the elements of a square matrix, plays a critical role in understanding the properties of matrices, such as whether a system of equations has a unique solution. By mastering operations on matrices and calculating determinants, you can approach a wide range of mathematical and real-world problems with ease.
Basic Matrix Operations
Before diving into determinants, it’s important to understand the basic operations that can be performed on matrices. These operations are fundamental to working with matrices in various applications:
- Matrix Addition: Matrices can be added if they have the same dimensions. The sum is obtained by adding corresponding elements.
- Scalar Multiplication: Each element of a matrix is multiplied by a scalar (a single number).
- Matrix Multiplication: Matrices can be multiplied if the number of columns in the first matrix equals the number of rows in the second. The result is a new matrix where each element is the sum of the products of corresponding entries.
Understanding Determinants
The determinant is a value that can be computed from the elements of a square matrix. It provides important information about the matrix, such as whether it is invertible. A non-zero determinant indicates that the matrix has an inverse, while a zero determinant suggests that the matrix is singular and does not have an inverse.
The determinant of a 2×2 matrix is calculated as follows:
For the matrix [[a, b], [c, d]], the determinant is:
det(A) = ad – bc
For larger matrices, the determinant is calculated using a method called cofactor expansion, which involves breaking down the determinant calculation into smaller determinants of submatrices.
Example of Determinant Calculation
Consider the following 2×2 matrix:
| a | b |
| c | d |
The determinant of this matrix is calculated as:
det(A) = ad – bc
If a = 2, b = 3, c = 4, and d = 5, then:
det(A) = (2)(5) – (3)(4) = 10 – 12 = -2
This value indicates that the matrix is invertible, as the determinant is not zero. A determinant of zero would indicate that the matrix is singular and does not have an inverse.
Working with matrices and determinants allows you to solve complex problems in areas such as systems of equations, transformations, and data analysis. By understanding the properties of matrices and the significance of their determinants, you can approach mathematical challenges with confidence and precision.
Graphing Rational Functions
Graphing rational functions involves plotting the behavior of ratios of polynomials. These functions can exhibit complex behaviors such as vertical asymptotes, horizontal asymptotes, and holes. Understanding the structure of the function and identifying key features are essential steps in graphing these types of functions accurately. By examining the numerator and denominator, you can predict the graph’s general shape and key characteristics.
Key Features of Rational Functions
When graphing rational functions, it’s important to identify and analyze the following key features:
- Vertical Asymptotes: These occur when the denominator of the rational function equals zero, causing the function to approach infinity. To find vertical asymptotes, set the denominator equal to zero and solve for the variable.
- Horizontal Asymptotes: Horizontal asymptotes describe the end behavior of the function as the variable approaches positive or negative infinity. These asymptotes depend on the degrees of the numerator and denominator polynomials.
- Holes: A hole occurs in the graph where a factor in both the numerator and denominator cancels out. To find holes, factor both the numerator and denominator and identify common factors.
- X-Intercepts: The x-intercepts are the points where the graph crosses the x-axis. These are found by setting the numerator equal to zero and solving for the variable.
- Y-Intercepts: The y-intercepts are found by substituting zero for the variable in the rational function.
Steps for Graphing a Rational Function
To graph a rational function, follow these steps:
- Factor both the numerator and denominator if possible.
- Find the vertical asymptotes by setting the denominator equal to zero and solving for the variable.
- Determine the horizontal asymptotes based on the degrees of the numerator and denominator.
- Look for any holes by identifying common factors in the numerator and denominator.
- Find the x- and y-intercepts by setting the appropriate values to zero and solving the equation.
- Plot key points and sketch the graph, ensuring it approaches the asymptotes as it moves toward infinity.
Example of Graphing a Rational Function
Consider the following rational function:
| f(x) = (x² – 1) / (x – 1) |
Let’s break it down step by step:
- Factor the function: f(x) = (x – 1)(x + 1) / (x – 1)
- Cancel the common factor: f(x) = x + 1 (with a hole at x = 1)
- Vertical Asymptote: There is a vertical asymptote at x = 1 because the denominator equals zero at x = 1 before cancellation.
- Horizontal Asymptote: Since the degree of the numerator (1) is equal to the degree of the denominator (1), the horizontal asymptote is y = 1.
- Intercepts: The x-intercept occurs when the numerator is zero, at x = -1. The y-intercept occurs when x = 0, yielding y = 1.
By following these steps and identifying the key features of the rational function, you can effectively sketch its graph and gain insight into its behavior across different regions.
Exploring Sequences and Series
In mathematics, sequences and series play a critical role in understanding patterns, growth, and the behavior of numbers over time. A sequence is a list of numbers that follow a specific pattern, while a series represents the sum of the terms in a sequence. By analyzing these structures, one can uncover various relationships and make predictions about future terms. These concepts have wide applications in fields ranging from finance to engineering, as they help model real-world phenomena.
Understanding Sequences
A sequence is an ordered list of numbers that follows a specific rule or pattern. The most common types of sequences are arithmetic and geometric, but many other types exist as well. The general term of a sequence can often be expressed as a formula, allowing you to predict future terms.
- Arithmetic Sequences: In an arithmetic sequence, the difference between consecutive terms is constant. This difference is called the common difference. For example, the sequence 3, 5, 7, 9, … has a common difference of 2.
- Geometric Sequences: A geometric sequence is a sequence in which each term is found by multiplying the previous term by a constant. This constant is called the common ratio. For example, 2, 6, 18, 54, … is a geometric sequence with a common ratio of 3.
Exploring Series
A series is the sum of the terms in a sequence. When working with series, we can use formulas to find the sum of a finite number of terms or to determine the sum of an infinite series under certain conditions. The two most common types of series are arithmetic and geometric series.
- Arithmetic Series: The sum of the terms in an arithmetic sequence is called an arithmetic series. The formula for the sum of the first n terms in an arithmetic series is:
| Sn = n/2 * (2a + (n – 1)d) |
| Where: |
| a = first term, d = common difference, n = number of terms |
- Geometric Series: A geometric series is the sum of the terms in a geometric sequence. The sum of the first n terms in a geometric series is given by the formula:
| Sn = a(1 – rn) / (1 – r) |
| Where: |
| a = first term, r = common ratio, n = number of terms |
For an infinite geometric series, if the common ratio r is between -1 and 1, the sum converges to:
| S = a / (1 – r) |
Applications of Sequences and Series
Sequences and series are used in various practical scenarios, including finance for calculating compound interest, in physics for modeling wave functions, and in computer science for analyzing algorithms. Understanding how these structures work can help solve real-world problems involving growth, decay, and recurring patterns.
Operations with Complex Numbers
Complex numbers extend the concept of numbers beyond the real number system, providing a way to handle solutions to equations that have no real solutions. These numbers consist of two parts: a real component and an imaginary component. The imaginary unit, represented as i, is defined as the square root of -1. By understanding operations with complex numbers, such as addition, subtraction, multiplication, and division, one can solve a wider range of mathematical problems.
Adding and Subtracting Complex Numbers
When adding or subtracting complex numbers, simply combine their real and imaginary parts separately. For example, to add the complex numbers (3 + 4i) and (2 + 5i), you would add the real parts (3 + 2) and the imaginary parts (4i + 5i), resulting in (5 + 9i). The same principle applies for subtraction–subtract the real parts and the imaginary parts accordingly.
Example:
(3 + 4i) + (2 + 5i) = (3 + 2) + (4i + 5i) = 5 + 9i
(7 + 3i) – (2 + 5i) = (7 – 2) + (3i – 5i) = 5 – 2i
Multiplying Complex Numbers
Multiplying complex numbers involves using the distributive property (also known as FOIL method for binomials) and applying the rule that i2 = -1. For example, multiplying (3 + 2i) by (4 + 5i) would require multiplying each term in the first complex number by each term in the second complex number and then simplifying the result.
Example:
(3 + 2i) × (4 + 5i) = 3(4) + 3(5i) + 2i(4) + 2i(5i)
= 12 + 15i + 8i + 10i2
= 12 + 23i – 10
= 2 + 23i
Dividing Complex Numbers

To divide complex numbers, multiply both the numerator and denominator by the conjugate of the denominator. The conjugate of a complex number is found by changing the sign of its imaginary part. This technique helps eliminate the imaginary part in the denominator, making the result a real number.
Example:
To divide (3 + 4i) by (1 – 2i), multiply both the numerator and denominator by the conjugate of (1 – 2i), which is (1 + 2i):
(3 + 4i) / (1 – 2i) × (1 + 2i) / (1 + 2i)
= (3 + 4i)(1 + 2i) / (1 – 2i)(1 + 2i)
= (3 + 6i + 4i + 8i2) / (1 + 4)
= (3 + 10i – 8) / 5
= (-5 + 10i) / 5
= -1 + 2i
Conjugates and Their Role
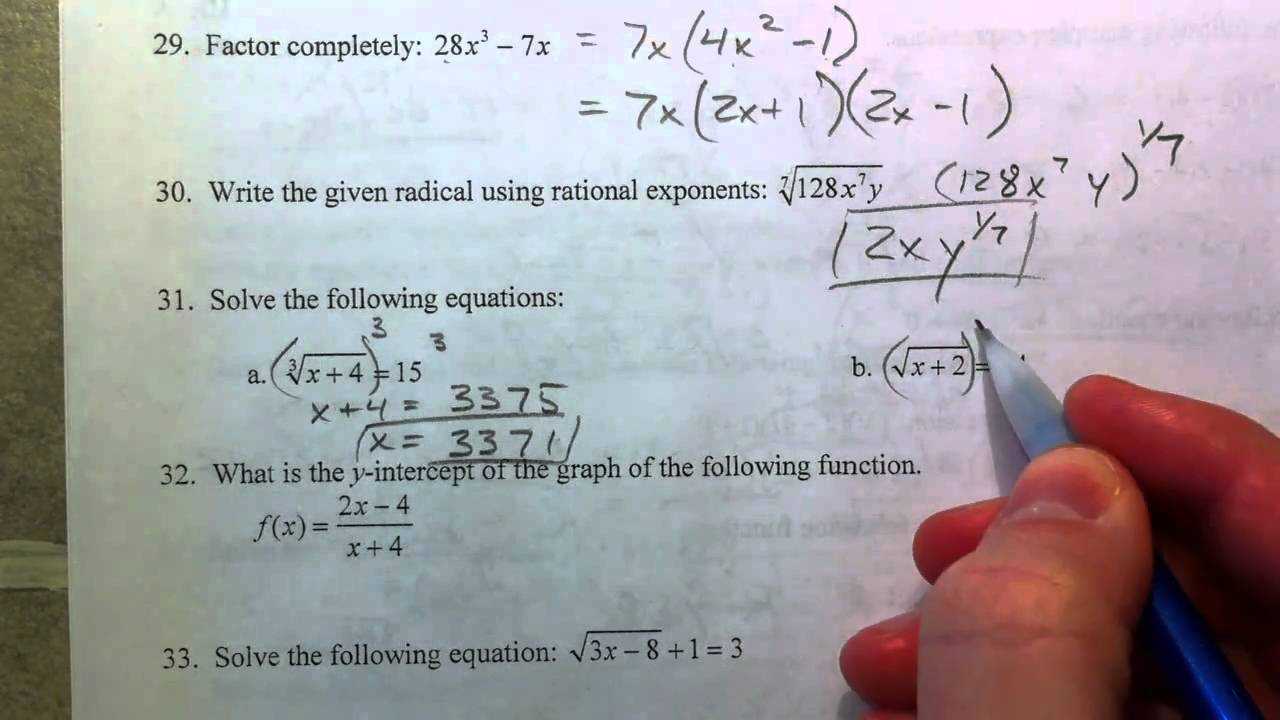
The conjugate of a complex number is useful in simplifying expressions involving complex numbers, especially in division. The conjugate of a + bi is a – bi, and multiplying a complex number by its conjugate yields a real number. This property is essential in rationalizing the denominator when dividing complex numbers.
Factoring Advanced Algebraic Expressions
Factoring is a key process in simplifying expressions and solving equations. In more complex cases, this process involves identifying patterns or techniques that allow you to break down an expression into simpler factors. By mastering advanced factoring methods, you can solve higher-level equations more efficiently, and gain a deeper understanding of polynomial behavior.
Factoring by Grouping
When dealing with expressions that have four terms, one of the most effective methods is factoring by grouping. This technique involves grouping terms in pairs, factoring each pair separately, and then finding the greatest common factor of the resulting binomials. The goal is to transform the expression into a product of two binomials, making it easier to solve or simplify further.
Example:
Factor the expression x2 + 5x + 2x + 10 by grouping:
1. Group the terms: (x2 + 5x) + (2x + 10)
2. Factor each group: x(x + 5) + 2(x + 5)
3. Factor out the common binomial: (x + 5)(x + 2)
Factoring Trinomials
Factoring trinomials, especially those where the leading coefficient is not 1, requires careful consideration. The method involves finding two numbers that multiply to give the product of the leading coefficient and the constant term, while also adding up to the middle coefficient. This technique is often referred to as “splitting the middle term” or “factor by decomposition.”
Example:
Factor 2x2 + 7x + 3:
1. Multiply the first and last coefficients: 2 × 3 = 6
2. Find two numbers that multiply to 6 and add to 7: 1 and 6
3. Rewrite the middle term as the sum of these two numbers: 2x2 + x + 6x + 3
4. Group and factor: x(2x + 1) + 3(2x + 1)
5. Final factorization: (x + 3)(2x + 1)
Solving Radical Equations
Solving equations involving roots requires a methodical approach to isolate the variable. The key is to eliminate the radical sign by raising both sides of the equation to the appropriate power. This process helps simplify the equation into a form that is easier to solve. However, it’s essential to check the solutions, as extraneous roots can sometimes appear after simplifying the equation.
Steps to Solve Radical Equations
To solve radical equations, follow these basic steps:
- Isolate the radical expression: Move all terms that do not involve the radical to the opposite side of the equation.
- Eliminate the radical: Raise both sides of the equation to the power that matches the root (for example, square both sides if there is a square root).
- Simplify the equation: After eliminating the radical, simplify the resulting equation as needed.
- Check for extraneous solutions: Substitute the solutions back into the original equation to verify they satisfy the equation.
Example: Solving a Square Root Equation
Consider the equation: √(x + 5) = 3. Let’s solve it step by step:
- Isolate the square root: The square root is already isolated on the left side of the equation.
- Square both sides: Squaring both sides removes the square root:
(√(x + 5))² = 3², which simplifies to x + 5 = 9. - Simplify: Subtract 5 from both sides to solve for x:
x = 9 – 5, so x = 4. - Check for extraneous solutions: Substitute x = 4 into the original equation:
√(4 + 5) = 3, which simplifies to √9 = 3. Since this is true, x = 4 is the solution.
Using the Binomial Theorem
The Binomial Theorem provides a powerful method for expanding expressions raised to a power. It allows you to write the expansion of a binomial raised to any exponent as a sum of terms. By using binomial coefficients, this theorem simplifies calculations and provides a systematic approach to dealing with complex expressions. Each term in the expansion consists of a coefficient and variables raised to specific powers, and the theorem makes it possible to calculate these terms without manually multiplying out the expression.
The Binomial Expansion Formula
The general form of the binomial expansion for (a + b)^n is given by:
(a + b)^n = Σ (n choose k) * a^(n-k) * b^k, where Σ denotes the summation over the terms from k = 0 to k = n, and (n choose k) represents the binomial coefficients. These coefficients are calculated using the formula:
(n choose k) = n! / (k! * (n – k)!)
Example: Expanding (x + 2)^3
Let’s apply the Binomial Theorem to expand (x + 2)^3:
- For n = 3, the binomial expansion formula gives us the following terms:
- Term 1: (3 choose 0) * x^(3-0) * 2^0 = 1 * x^3 * 1 = x^3
- Term 2: (3 choose 1) * x^(3-1) * 2^1 = 3 * x^2 * 2 = 6x^2
- Term 3: (3 choose 2) * x^(3-2) * 2^2 = 3 * x * 4 = 12x
- Term 4: (3 choose 3) * x^(3-3) * 2^3 = 1 * 1 * 8 = 8
Now, combine all terms: x^3 + 6x^2 + 12x + 8.
Analyzing Functions and Their Behavior
Understanding how functions behave is essential in various mathematical fields. By examining a function’s characteristics, such as its domain, range, and key points like intercepts and extrema, we gain insight into its graph and overall behavior. Identifying the trends of a function, whether it’s increasing, decreasing, or constant, can provide valuable information for solving real-world problems and making predictions. Functions can exhibit a variety of behaviors, and being able to analyze these patterns helps in making informed decisions about their applications.
Identifying Key Features
When analyzing a function, it’s important to focus on several key aspects:
- Domain and Range: The set of input values (domain) and the corresponding output values (range) are critical for understanding the scope of the function.
- Intercepts: The points where the function crosses the x-axis (x-intercepts) and the y-axis (y-intercepts) can reveal important information about its graph.
- Increasing and Decreasing Intervals: Identifying where the function is increasing or decreasing can help describe its overall shape and behavior.
- Extrema: Local maxima and minima, or turning points, highlight where the function changes direction.
Example: Analyzing a Quadratic Function
Consider the function f(x) = x^2 – 4x + 3. To analyze its behavior, we begin by finding its key features:
- Domain: All real numbers, since there are no restrictions on the values of x.
- Range: The function opens upward, so the minimum value occurs at the vertex. The range is [3, ∞).
- Intercepts: The x-intercepts occur when f(x) = 0, or x^2 – 4x + 3 = 0. Factoring, we get (x – 1)(x – 3) = 0, so the intercepts are x = 1 and x = 3. The y-intercept occurs when x = 0, giving f(0) = 3.
- Extrema: The vertex of the parabola is located at x = -(-4)/2(1) = 2, so the minimum value is f(2) = -1.
By studying these features, we can gain a clearer understanding of how the function behaves and how its graph is shaped. This approach can be applied to a wide variety of functions to predict their behavior under different conditions.
Application of Mathematics in Real Life
Mathematics plays a crucial role in solving everyday problems and is used in various fields, from business to engineering, to make informed decisions. Understanding mathematical principles can help individuals make predictions, calculate costs, optimize resources, and analyze data. Whether you’re managing finances, designing structures, or planning a trip, the skills learned in mathematical problem-solving are indispensable in real-world situations.
Everyday Applications
Here are a few examples of how mathematical concepts are applied in daily life:
- Budgeting and Personal Finance: Calculating expenses, setting up savings plans, and investing in the stock market all require a strong understanding of mathematical operations and problem-solving strategies.
- Home Improvement: Whether you’re tiling a floor, painting a wall, or building a fence, measuring dimensions, calculating areas, and estimating quantities all involve mathematical reasoning.
- Cooking and Recipe Adjustments: When scaling recipes, understanding proportions and fractions is essential for adjusting ingredients based on the number of servings needed.
- Travel Planning: Determining the best route, estimating travel time, and calculating fuel costs all require mathematical computations and data analysis.
Applications in Various Professions
Professionals in many fields also rely on mathematical principles to solve complex problems:
- Engineering: Structural engineers use math to design safe buildings, bridges, and roads by calculating loads, forces, and stress.
- Medicine: Medical professionals use statistics to analyze patient data, create dosage calculations, and make predictions about health trends.
- Technology: Computer scientists and programmers use mathematical algorithms to develop software, create encryption methods, and design artificial intelligence systems.
- Economics: Economists use mathematical models to analyze market trends, predict economic growth, and make policy recommendations.
As these examples show, mathematical skills are essential tools for understanding the world around us and for making informed decisions in various aspects of life.
Common Mistakes to Avoid
When working with mathematical problems, certain errors are frequently made, especially under time constraints or when under pressure. Understanding and avoiding these common pitfalls can lead to better accuracy and efficiency. Being mindful of small details and reviewing work carefully can help ensure that the solutions are correct and the steps are properly followed. Below are some of the most common mistakes and tips on how to avoid them.
Key Errors to Watch Out For

Here are a few common mistakes and how they can be prevented:
| Type of Mistake | How to Avoid It |
|---|---|
| Sign Errors | Double-check each sign in the equation, especially when multiplying or dividing negative numbers. A common mistake is forgetting to flip the sign during these operations. |
| Misinterpreting Word Problems | Carefully read each word problem and underline key information. Break the problem down into smaller steps and identify what is being asked before proceeding. |
| Overlooking Units | Always keep track of the units in word problems. Forgetting to convert units or use the correct unit conversions can lead to incorrect answers. |
| Errors in Distribution | When distributing terms in expressions, make sure to apply the distributive property correctly. Pay close attention when multiplying terms inside parentheses. |
| Skipping Steps | While it’s tempting to skip intermediate steps to save time, this often leads to mistakes. Always show your work and check that every step makes sense before moving forward. |
| Ignoring Restrictions | For rational expressions or equations, never forget to check for restrictions where the denominator could be zero. These restrictions are critical for finding valid solutions. |
Double-Check Your Work
After solving a problem, take a moment to review the steps carefully. Recheck calculations, especially when dealing with complex numbers, fractions, or exponents. Verifying your solution not only helps in catching errors but also boosts confidence in your results.