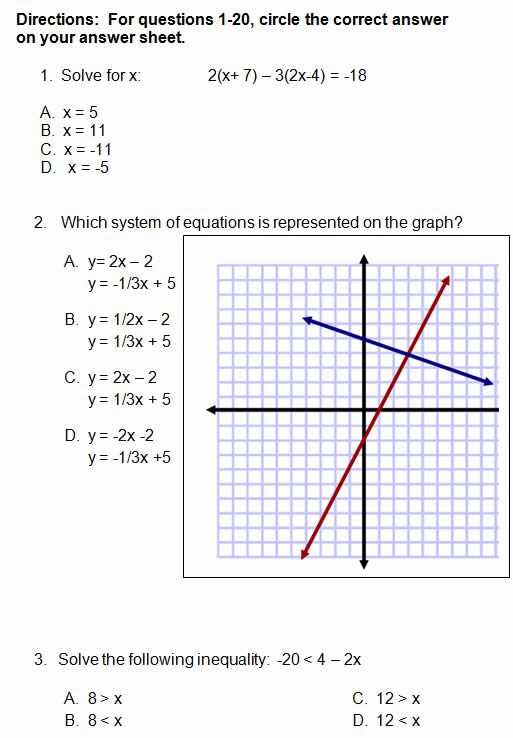
Preparing for a major math assessment can be a challenging yet rewarding process. The key to success lies in mastering essential techniques and understanding the core principles that are tested. Whether you’re solving equations, working with graphs, or tackling word problems, a strong foundation is crucial for confident performance.
Effective study strategies involve not only reviewing your coursework but also practicing a variety of problem types. By focusing on common problem-solving methods and familiarizing yourself with the format, you can approach your assessment with ease and clarity. The right approach will help you build confidence and improve your accuracy when it counts.
Throughout your preparation, it’s important to recognize areas that may need extra attention. With consistent practice and strategic review, you’ll develop the skills necessary to excel in your assessment and feel ready to tackle any challenge it presents.
Mastering Key Problem Solving Techniques
To succeed in any mathematical assessment, it’s essential to not only understand the theory but also to develop strong problem-solving skills. The process involves recognizing patterns, applying formulas correctly, and managing time effectively during the test. The ability to navigate through different types of questions with confidence is what leads to success.
Core Strategies for Tackling Problems
Approaching each question with a clear strategy is crucial. Start by breaking down the problem into smaller, manageable parts. This method allows you to focus on one step at a time, reducing the risk of errors and improving your overall performance. Whether you’re dealing with equations, inequalities, or graphing, understanding the underlying principles will guide your solutions.
Common Challenges and How to Overcome Them

Many students struggle with specific problem types, such as solving for unknown variables or interpreting word problems. To overcome these obstacles, practice is key. Working through practice questions will help familiarize you with the common traps and enhance your ability to recognize patterns. Remember, every mistake is an opportunity to improve your skills and approach.
Staying focused and managing your time wisely are just as important as your mathematical knowledge. With the right mindset and preparation, you can approach any challenge and solve it effectively. Keep practicing, and soon, you’ll feel confident and prepared for any task that comes your way.
Understanding Key Mathematical Concepts

Grasping the fundamental concepts of mathematics is essential for tackling complex problems with confidence. By developing a strong understanding of core principles, such as operations, relationships, and functions, you can approach problems logically and methodically. These concepts form the foundation upon which more advanced topics are built, and mastering them is crucial for success.
Key ideas such as manipulating variables, solving equations, and working with expressions are central to many problems. Whether you are simplifying terms, factoring polynomials, or solving systems of equations, having a clear grasp of these techniques will enable you to work through a variety of challenges effectively. Practicing these skills ensures that you can apply them in different contexts, making problem-solving more intuitive and less daunting.
Additionally, developing a deeper understanding of graphing and interpreting functions can help you visualize problems and identify solutions more efficiently. This insight is essential not just for exams, but for applying mathematical knowledge to real-world situations. Mastering these core concepts will allow you to tackle any challenge with clarity and precision.
Important Topics for Mathematical Assessment
When preparing for a major test, it’s crucial to focus on the key areas that are most commonly covered. These topics form the foundation of the material and are essential for solving a variety of problems. Mastering these areas will not only improve your problem-solving skills but also boost your confidence and ability to handle different types of questions.
Core Areas to Focus On
To perform well, concentrate on understanding core concepts that frequently appear in assessments. Key areas include working with equations, understanding inequalities, and interpreting graphs. By focusing on these areas, you’ll be able to tackle most questions with confidence and accuracy.
Key Formulas and Techniques
Knowing the right formulas and methods is essential for solving complex problems quickly. Below is a table highlighting some of the most important techniques you should be familiar with:
| Topic | Key Formula/Technique |
|---|---|
| Solving Linear Equations | Use inverse operations to isolate the variable |
| Factoring Quadratics | Find two numbers that multiply to the constant and add to the middle coefficient |
| Working with Inequalities | Apply similar steps as solving equations, but reverse the inequality symbol when multiplying/dividing by a negative number |
| Graphing Functions | Plot key points and use slope and intercepts |
Focusing on these core areas and practicing related problems will ensure that you are well-prepared for any type of question you might face.
How to Solve Algebraic Equations
Solving mathematical equations is a fundamental skill that requires a clear, step-by-step approach. The process of finding the value of an unknown variable involves isolating it on one side of the equation. With practice, this technique becomes second nature, and you’ll be able to tackle more complex problems with confidence.
Here’s a general method for solving most equations:
- Start by simplifying both sides of the equation if necessary (combine like terms or distribute).
- Next, use inverse operations to move terms involving the unknown to one side of the equation.
- Isolate the variable by performing operations that leave it alone on one side.
- Finally, solve for the variable and check your solution to ensure it satisfies the original equation.
Let’s look at an example:
Consider the equation: 3x + 5 = 20
- Subtract 5 from both sides: 3x = 15
- Now, divide both sides by 3: x = 5
Once you’ve solved for the variable, always substitute the solution back into the original equation to verify that both sides are equal. This step ensures your solution is correct.
By following these steps, you can confidently solve a wide variety of equations, whether simple or more complex. Practice is the key to mastering this technique and solving problems accurately and efficiently.
Step-by-Step Solutions for Mathematical Problems
When solving mathematical problems, breaking the process into manageable steps is essential for clarity and accuracy. By following a structured approach, you can systematically work through challenges and ensure that you arrive at the correct solution. This method helps you avoid errors and understand the reasoning behind each step.
General Approach for Solving Problems
Here’s a step-by-step guide to solving most mathematical problems:
- Start by reading the problem carefully and identifying the key components, such as the unknown variable and the given information.
- Write down any relevant equations or relationships that can help you solve the problem.
- Simplify the problem by combining like terms or factoring where possible.
- Apply the appropriate mathematical operations, such as addition, subtraction, multiplication, or division, to move towards isolating the variable.
- Once the variable is isolated, solve for its value and ensure that the result is correct by substituting it back into the original problem.
Example Problem
Let’s go through a sample problem:
Problem: Solve for x in the equation 4x + 7 = 23
- Start by subtracting 7 from both sides: 4x = 16
- Next, divide both sides by 4: x = 4
- Finally, substitute x = 4 back into the original equation: 4(4) + 7 = 23, which simplifies to 16 + 7 = 23. Since both sides are equal, the solution is correct.
By following these steps and practicing regularly, you can solve a wide range of problems with confidence and efficiency.
Common Mistakes in Mathematical Assessments
Many students encounter recurring challenges when solving problems in mathematics. These common mistakes often arise from simple miscalculations, overlooked details, or a misunderstanding of key concepts. Recognizing these pitfalls can help you avoid them and improve your performance during any assessment.
Frequent Errors to Watch Out For
Here are some typical mistakes that students make:
- Forgetting to distribute terms correctly when dealing with parentheses.
- Incorrectly isolating the variable, especially when dealing with fractions or negative numbers.
- Misinterpreting word problems, leading to the wrong setup of the equation.
- Skipping steps, which can result in errors that compound as you work through the problem.
- Making calculation errors during the final steps, especially when working under time pressure.
How to Avoid These Mistakes
To avoid these issues, take a systematic approach to each problem:
- Always check your work step by step, ensuring that each operation is performed correctly.
- Re-read word problems carefully to ensure the equation is set up accurately.
- Practice regularly with a variety of problem types to become more comfortable with different scenarios.
- Stay organized and don’t rush–take the time to review your calculations and steps before finalizing your answer.
By being aware of these common errors and following a structured approach, you can avoid these pitfalls and improve your problem-solving accuracy.
Tips for Efficient Test Preparation
Effective preparation is the key to performing well in any assessment. By organizing your study routine and focusing on the most important areas, you can maximize your learning and reduce unnecessary stress. Efficient preparation not only boosts your confidence but also helps you manage your time effectively during the assessment.
Key Strategies for Success
To make your preparation more effective, consider the following tips:
- Start early to avoid cramming and give yourself ample time to review all key topics.
- Break down your study material into smaller, manageable sections to focus on one topic at a time.
- Use practice problems to reinforce your understanding and identify areas where you need improvement.
- Prioritize the areas that are most likely to appear in the assessment and that you find most challenging.
- Take regular breaks to prevent burnout and maintain focus throughout your study sessions.
Effective Study Techniques
In addition to time management, using the right study techniques can further enhance your preparation:
- Create a study schedule to structure your time and ensure you cover all topics thoroughly.
- Review past problems and questions to familiarize yourself with the format and types of questions you might face.
- Collaborate with peers for group study sessions to discuss concepts and clarify doubts.
- Teach what you’ve learned to others, as explaining concepts reinforces your understanding.
By following these strategies and staying organized, you can ensure that your preparation is focused and productive, leading to better performance when it counts.
Mastering Word Problems in Mathematics
Word problems often present a unique challenge in math assessments, requiring the ability to translate real-world scenarios into mathematical expressions. Successfully solving these problems involves identifying key information, setting up equations, and applying the correct methods to find a solution. With practice, word problems become more approachable and less intimidating.
Breaking Down the Problem
The first step in solving any word problem is carefully reading the question to identify important details. Start by looking for:
- What is being asked? Understand the goal of the problem.
- What information is given? Identify numbers, variables, and relationships.
- What operations are involved? Look for keywords that suggest addition, subtraction, multiplication, or division.
Steps to Solve Word Problems
Once you’ve identified the necessary information, follow these steps:
- Translate the word problem into a mathematical equation or expression.
- Solve the equation step by step, following the order of operations.
- Check your solution to ensure it makes sense in the context of the problem.
Example Problem
Let’s consider a word problem example:
A car travels 60 miles per hour. How long will it take to travel 180 miles?
To solve this, we know the formula for time is:
| Formula | Time = Distance ÷ Speed |
|---|---|
| Given Data | Distance = 180 miles, Speed = 60 miles/hour |
Now, substitute the values into the formula:
- Time = 180 miles ÷ 60 miles/hour
- Time = 3 hours
The car will take 3 hours to travel 180 miles. By breaking down the problem and applying the right formula, we easily found the solution.
Strategies for Time Management During Assessments
Effective time management is essential for performing well under pressure during any assessment. By organizing your time wisely, you can ensure that you have enough opportunity to complete each section, review your work, and avoid rushing through questions. Planning ahead and staying focused during the test can help you use your time efficiently, allowing for a more relaxed and thorough approach.
Key Time Management Tips
Consider these strategies to help manage your time effectively:
- Arrive early to settle in and ensure you are prepared for the test.
- Skim through the entire assessment first to get a sense of the questions and how much time each section might require.
- Divide your available time equally between all sections of the test, ensuring you don’t spend too long on one question.
- Prioritize questions you feel most confident about to secure easy points early on.
- If a question is taking too long, move on and come back to it later if time permits.
How to Stay on Track

Staying on track is crucial to completing all sections of the assessment. Here’s how to ensure you don’t lose focus:
- Use a watch or clock to keep track of the time throughout the assessment.
- Take quick mental breaks during transitions between sections to stay fresh and avoid burnout.
- Review your answers only after completing all questions to avoid wasting valuable time in the middle of the test.
- Don’t obsess over a single difficult question. Move forward and leave enough time for review at the end.
By employing these time management strategies, you can increase your chances of finishing the test successfully, with enough time for reviewing and ensuring accuracy in your answers.
Reviewing Key Formulas and Rules
Understanding the essential formulas and rules is crucial for solving problems accurately and efficiently in any assessment. These foundational principles guide you through various mathematical tasks, from basic operations to more complex equations. By reviewing these concepts and committing them to memory, you can improve your ability to solve problems quickly and with confidence.
Below are some of the most important formulas and rules you should remember:
- Order of Operations: Always follow the correct sequence–Parentheses, Exponents, Multiplication and Division (from left to right), Addition and Subtraction (from left to right). This is often abbreviated as PEMDAS.
- Distributive Property: This rule allows you to multiply a single term by each term inside a set of parentheses. For example, a(b + c) = ab + ac.
- Solving Linear Equations: To isolate the variable, perform inverse operations on both sides of the equation. For instance, if x + 5 = 12, subtract 5 from both sides to get x = 7.
- Factoring Quadratics: Factor expressions of the form ax^2 + bx + c = 0 by finding two numbers that multiply to ac and add to b.
- Properties of Exponents: For example, x^m * x^n = x^(m+n) and (x^m)^n = x^(m*n). Understanding these properties helps in simplifying expressions.
Mastering these rules allows for more efficient problem-solving and helps you feel more confident when tackling complex questions in any assessment scenario.
How to Tackle Multiple Choice Questions
Multiple choice questions can be tricky, as they often require you to think critically and rule out incorrect options. To perform well in this format, it’s essential to have a clear strategy. The key is to approach each question methodically and not rush through the options. By following a few simple steps, you can increase your chances of selecting the right answer even when you’re unsure.
Step-by-Step Approach
Here’s a strategy to help you tackle multiple choice questions effectively:
- Read the Question Carefully: Before looking at the options, make sure you understand the problem. Pay attention to key words and any special instructions.
- Analyze All Options: Don’t jump to the first answer that seems correct. Read through all choices carefully, as there may be subtle differences between them.
- Eliminate Clearly Incorrect Answers: If you’re sure that one or more options are wrong, cross them out mentally or physically. This increases your chances of choosing the correct answer from the remaining options.
- Consider Logical Reasoning: If you’re stuck between two choices, try to reason out the answer. Sometimes, eliminating absurd choices or using logic can guide you to the right one.
- Trust Your First Instinct: Often, your first answer is the right one. If you have to guess, go with your initial choice unless you find a compelling reason to change it.
Tips for Success
- Watch for Keywords: Words like “always,” “never,” “all,” or “none” can be helpful indicators. For instance, an answer that says “always” is often too extreme to be correct.
- Manage Your Time: Don’t dwell too long on one question. If you’re unsure, make your best guess and move on. You can always come back to it if time allows.
- Check for Hidden Clues: Sometimes, other questions on the test may provide clues or help you eliminate incorrect options in a multiple choice question.
By staying focused and following a clear process, you can improve your ability to answer multiple choice questions accurately and efficiently.
Focus Areas for Mathematical Success
To achieve success in mathematical assessments, it’s essential to concentrate on key areas that form the foundation of problem-solving skills. Strengthening these focus areas helps build confidence and ensures a solid understanding of the concepts. When you prioritize these essential topics, you’ll be better prepared to handle more complex problems efficiently and accurately.
Below are the critical focus areas that should be emphasized for success:
| Topic | Key Focus |
|---|---|
| Linear Equations | Master the art of solving equations by isolating the variable and using inverse operations to simplify expressions. |
| Exponents and Powers | Understand the properties of exponents and how to apply them to simplify expressions involving powers and roots. |
| Factoring | Learn to factor polynomials and quadratic expressions, recognizing patterns and using techniques like grouping and splitting terms. |
| Systems of Equations | Focus on solving systems using substitution, elimination, or graphing methods for efficient solutions. |
| Inequalities | Understand how to solve and graph inequalities, including linear inequalities and compound inequalities. |
By consistently focusing on these core areas, you’ll be able to build a solid mathematical foundation that will support you through more challenging topics and assessments.
Handling Negative Numbers in Mathematics
Negative numbers can be challenging when solving mathematical problems, but they are an essential part of understanding many concepts. Mastering how to work with these values is crucial for progressing through various topics. Whether adding, subtracting, multiplying, or dividing, it’s important to apply the correct rules and strategies for handling negative numbers in different situations.
Key Rules for Negative Numbers
- Addition of Negative Numbers: When adding two negative numbers, the result is always negative. For example, -3 + -5 = -8.
- Subtraction of Negative Numbers: Subtracting a negative number is the same as adding its positive counterpart. For instance, 7 – (-2) = 7 + 2 = 9.
- Multiplication of Negative Numbers: When multiplying two negative numbers, the result is positive. For example, -4 × -3 = 12. If one number is negative, the result is negative.
- Division of Negative Numbers: The same rule applies as with multiplication. Dividing two negative numbers results in a positive answer, while dividing a positive by a negative number results in a negative answer. For example, -8 ÷ -2 = 4, while 8 ÷ -2 = -4.
Strategies for Solving Problems with Negative Numbers
- Keep Track of Signs: Always be aware of the signs involved in the operation. A good habit is to rewrite expressions to make sure the signs are clear before solving.
- Use a Number Line: A number line can be a helpful visual aid when adding or subtracting negative values. It helps to see how far to move left or right from a given point.
- Practice Mental Math: With enough practice, mental calculations involving negative numbers become quicker and easier. Try simplifying the problem step by step in your head.
By familiarizing yourself with these rules and strategies, you will become more confident and accurate when solving problems that involve negative values in mathematical contexts.
How to Use Graphs in Mathematics
Graphs are powerful tools for visualizing mathematical relationships and understanding patterns. By plotting equations and expressions on a graph, you can quickly interpret complex concepts and make informed conclusions. Whether working with linear relationships or more intricate functions, graphs provide a visual representation that aids in solving problems and explaining mathematical ideas.
Understanding the Coordinate System
Before using graphs effectively, it’s important to understand the basic coordinate system. The x-axis and y-axis form the grid where all points are plotted. Each point is represented as an ordered pair (x, y), where x is the horizontal position and y is the vertical position. The intersection of these axes is called the origin, which has the coordinates (0, 0).
Plotting Points and Interpreting Graphs
- Plotting Points: To plot a point on a graph, start at the origin and move along the x-axis to the value of x, then move vertically along the y-axis to the value of y. Mark the point where these two movements intersect.
- Interpreting Graphs: Once the points are plotted, you can draw lines or curves to represent the relationships between them. The resulting graph can show trends, such as increasing or decreasing values, and help you understand how different variables interact.
- Finding Solutions: Graphs allow you to visually find solutions to equations. For example, if you’re working with a linear equation, the solution is where the line intersects the x-axis or y-axis.
By practicing these techniques, you’ll be able to use graphs to simplify and solve mathematical problems more efficiently, making the concepts clearer and easier to understand.
Real-World Applications of Mathematics
Mathematics plays a crucial role in various aspects of everyday life. It helps solve practical problems, make informed decisions, and improve efficiency in many fields. From budgeting personal finances to designing structures, mathematical concepts provide the foundation for solutions that are both practical and essential in real-world scenarios. Understanding how to apply these concepts allows us to navigate daily challenges with confidence and accuracy.
Finance and Budgeting
One of the most common uses of mathematical principles is in financial planning and budgeting. Whether managing personal expenses, calculating savings, or planning for large investments, mathematical formulas help ensure that individuals and businesses can allocate resources wisely. For example, understanding interest rates, loan repayments, and investment growth requires using equations that model financial systems.
Engineering and Design
Mathematical concepts are fundamental to engineering, architecture, and design. Engineers use mathematical models to calculate dimensions, forces, and structural integrity when designing buildings, bridges, and other infrastructure. Geometry and trigonometry are often used to determine angles, distances, and load-bearing capacities. Additionally, mathematical equations help to optimize designs, ensuring efficiency and safety in construction projects.
These are just a few examples of how mathematical thinking applies to real-world challenges. By mastering mathematical techniques, individuals can make better decisions and tackle a wide range of problems more effectively in both personal and professional contexts.
How to Check Your Solutions Effectively
Verifying the accuracy of your solutions is a crucial step in ensuring that your work is correct. Whether you’re solving mathematical problems or tackling complex questions, taking the time to check your work helps identify errors and confirms the validity of your results. A systematic approach to reviewing your steps can prevent simple mistakes and improve your overall problem-solving skills.
Step-by-Step Review Process

To effectively check your solutions, follow these guidelines:
- Revisit the problem: Start by reading the problem carefully again. Understand what is being asked and confirm that you are solving for the correct unknowns.
- Check each calculation: Go through every step of your solution process to ensure that no arithmetic errors were made. Double-check operations like addition, subtraction, multiplication, and division.
- Use a different method: If possible, try solving the problem in an alternative way or use estimation to see if your solution is reasonable.
- Verify the final solution: Plug your solution back into the original equation or problem to check if it satisfies the conditions given in the question.
Using a Table for Verification
Sometimes, organizing your work in a table format can help you see the relationships between different parts of the problem and identify any discrepancies. Here’s an example of how you might lay out your steps:
| Step | Operation | Result |
|---|---|---|
| 1 | Initial equation setup | Example: x + 3 = 7 |
| 2 | Solve for x | x = 4 |
| 3 | Check solution | 4 + 3 = 7 (True) |
This approach not only helps in confirming your final solution but also provides a clear view of your logical process, making it easier to spot any errors.
What to Do on Test Day
Test day is crucial for demonstrating your knowledge and problem-solving abilities. It is important to be prepared mentally, physically, and emotionally to ensure that you perform at your best. Having a strategy in place for the day of the assessment can help reduce stress and maximize your success. The following tips outline the key actions to take on the day of the test.
Before the Test
Proper preparation starts long before the actual assessment begins. Here’s what to do before you arrive:
- Get a good night’s sleep: Rest is essential for cognitive function. Aim for at least 7-8 hours of sleep the night before.
- Eat a healthy breakfast: A nutritious meal will give you the energy you need to stay focused and alert throughout the test.
- Review key concepts: Quickly go over any important formulas, rules, or strategies. Don’t try to learn new material at the last minute.
- Gather your materials: Ensure you have everything you’ll need, such as pens, pencils, a calculator (if allowed), and any other necessary tools.
During the Test
Once you begin the test, it’s essential to manage your time and approach each question methodically:
- Read each question carefully: Take time to understand what is being asked before jumping into your solution.
- Start with easier questions: Tackle the questions you find simplest first. This will build confidence and help manage your time more effectively.
- Time management: Keep an eye on the clock to ensure you’re allocating your time appropriately. Don’t spend too long on one question.
- Stay calm and focused: If you encounter a difficult problem, take a deep breath and move on. You can always return to it later.
By following these steps, you’ll be well-prepared to handle test day with confidence and clarity, ensuring that you give your best effort.
Resources for Further Algebra Practice
Mastering mathematical concepts requires continuous practice and exposure to different problem-solving scenarios. Whether you’re reinforcing your skills or tackling more advanced material, having the right resources can significantly enhance your understanding. Below are some effective tools and platforms to further develop your proficiency in solving mathematical problems.
Online Platforms
Online resources provide interactive exercises and immediate feedback, which can help you identify areas for improvement. Some valuable platforms include:
- Khan Academy: Offers comprehensive lessons and practice exercises on a variety of topics, from basic to advanced concepts.
- Wolfram Alpha: A powerful tool for solving problems and visualizing results, helping you understand the step-by-step process behind solutions.
- IXL: Provides personalized practice, allowing you to focus on areas where you need the most improvement.
Books and Study Guides
Books and printed materials can be an excellent complement to online learning. Here are some recommended resources:
- “The Complete Idiot’s Guide to Math Word Problems”: This book provides clear explanations and practice problems to improve problem-solving skills.
- “Problem-Solving Strategies for Math”: A helpful guide offering techniques and strategies for approaching complex problems in a logical way.
Practice Workbooks
Workbooks can offer structured exercises to reinforce key skills. These resources often provide a wide variety of problems, ranging from simple to challenging:
- “Math Problem-Solving Workbook”: Includes a wide range of problems for practice, with solutions to help verify your answers.
- “Mastering Mathematical Concepts Workbook”: Focuses on building mastery in key areas through consistent practice.
By leveraging these resources, you can effectively strengthen your skills and gain confidence in solving mathematical challenges. Consistent practice is essential for mastering any subject, so continue to explore these tools as part of your ongoing learning journey.