
In any academic pursuit involving data analysis, a clear understanding of core principles is essential to excel. This section focuses on key methods and techniques to help navigate complex numerical challenges with confidence. Whether you’re dealing with basic calculations or more advanced problem-solving scenarios, mastering these approaches will significantly enhance your performance.
Effective preparation for mathematical assessments requires a combination of practical skills and theoretical knowledge. Familiarity with various problem types and an ability to identify appropriate solutions are crucial. This guide will explore common techniques, provide insights into efficient strategies, and offer tips for overcoming obstacles commonly faced during evaluations.
By breaking down each area systematically, you’ll gain a deeper understanding of how to approach different types of tasks. Whether it’s interpreting data, applying formulas, or solving intricate equations, learning how to analyze each situation methodically will help you achieve better results.
Statistics Questions and Answers for Exams
When preparing for assessments that focus on data analysis, it’s important to familiarize yourself with the types of challenges that may arise. A thorough understanding of key concepts and techniques will allow you to tackle each problem with confidence. This section will guide you through various problem-solving scenarios, providing valuable insights on how to approach them effectively.
In this guide, you will encounter common problem types that often appear in academic tests. Each example will offer step-by-step guidance, highlighting critical strategies for identifying solutions. Mastering these approaches ensures you can handle both basic tasks and more complex situations with ease.
By practicing with these examples, you will gain the skills necessary to work through similar challenges on your own. The goal is to become proficient in identifying the most efficient methods for solving each type of task, allowing you to maximize your performance under time constraints.
Understanding Common Statistical Concepts
To excel in assessments focused on data analysis, it’s essential to grasp fundamental principles that form the foundation of problem-solving techniques. These core ideas are crucial for interpreting results, drawing conclusions, and making informed decisions. Understanding them will not only boost your ability to handle different scenarios but also enhance your overall analytical skills.
Some key concepts that often appear in such evaluations include:
- Measures of Central Tendency: These values summarize a data set by identifying a central point. Common examples include the mean, median, and mode.
- Dispersion: Understanding how data varies or spreads is vital. Key measures here include variance and standard deviation.
- Probability: The likelihood of an event occurring based on observed data. It plays a significant role in making predictions and testing hypotheses.
- Correlation: This concept examines the relationship between two variables and whether one affects the other.
- Sampling: The process of selecting a subset of data from a larger population to make inferences about the whole.
Mastering these ideas provides a solid base for tackling more complex problems and allows for accurate data interpretation. Understanding their applications will give you the confidence to apply the right techniques, regardless of the challenge at hand.
How to Approach Statistics Exam Questions
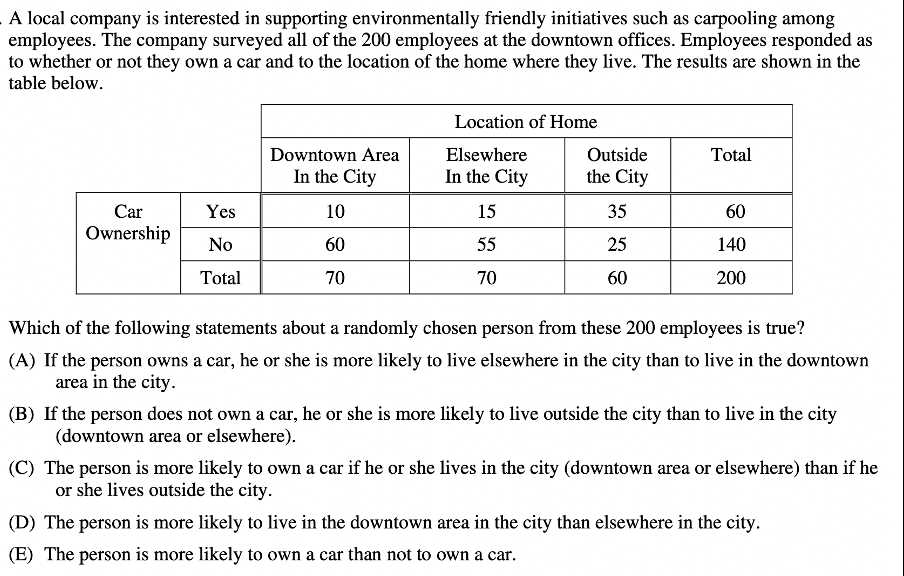
When tackling complex problems in any assessment focused on data analysis, it’s crucial to approach each task methodically. By understanding the structure of the problem and identifying key elements, you can devise an efficient strategy for solving it. The right approach not only helps in managing time effectively but also increases the accuracy of your solutions.
Begin by carefully reading each problem to understand what is being asked. Break down the information given and determine the relevant details that will lead to the solution. It’s often helpful to underline or highlight important data points to ensure nothing is overlooked.
Next, identify which techniques or formulas are applicable. Reflect on similar problems you have encountered during your preparation and think about the steps you took to solve them. This will guide you through the process of applying the correct methods. When possible, organize your work clearly, using appropriate notation to avoid confusion.
It’s also important to assess your solution once you’ve completed the calculations. Double-check your work for any errors and ensure that the final result makes sense in the context of the problem. If you have time, review your approach and ensure no critical steps were missed.
Key Formulas Every Student Should Know

In order to tackle numerical challenges effectively, it’s essential to master the fundamental equations that are frequently used in problem-solving. These core formulas are the building blocks for many tasks and will serve as the foundation for more advanced techniques. Understanding them thoroughly will save time and ensure accuracy when working under pressure.
Basic Calculation Methods

Several formulas are critical for basic calculations, especially when dealing with measures of central tendency or variability. The most commonly used are:
- Mean: Mean = (Sum of all values) / (Number of values)
- Median: The middle value when the data set is arranged in order.
- Mode: The value that appears most frequently in the data set.
Advanced Techniques

For more complex scenarios, other formulas are necessary, particularly when working with probability, correlation, or regression analysis. Some essential formulas include:
- Variance: Variance = (Sum of squared differences from the mean) / (Number of data points)
- Standard Deviation: Standard Deviation = √Variance
- Linear Regression Equation: y = mx + b, where m is the slope and b is the y-intercept.
By familiarizing yourself with these key formulas, you’ll be well-equipped to handle a wide range of problems efficiently. These equations form the foundation of many analytical methods and are indispensable tools for success in data-based assessments.
Tips for Solving Probability Problems

When faced with challenges involving likelihood or chance, it’s important to approach them with a structured mindset. By breaking down the problem and understanding the relationships between different events, you can apply the appropriate strategies to find the solution. These problems often require careful thought and methodical application of principles to arrive at the correct result.
Here are some helpful tips to keep in mind when solving probability-related tasks:
- Understand the Problem Clearly: Before jumping into calculations, read the problem carefully and identify all given information. Make sure you understand the events involved and what you’re asked to find.
- Determine Total Outcomes: In many cases, you need to know the total number of possible outcomes. Identify the sample space and the events you’re dealing with to ensure you’re counting the right possibilities.
- Use Simple Probability Formula: The basic formula for calculating probability is P(event) = (Number of favorable outcomes) / (Total number of outcomes). Apply this when the problem asks for the likelihood of a single event occurring.
- Consider Conditional Probability: If events are dependent on each other, remember to apply conditional probability. The formula P(A|B) = P(A ∩ B) / P(B) helps in such situations.
- Check for Mutually Exclusive or Independent Events: If events don’t influence each other, use the multiplication rule for independent events. If they can’t happen together, use the addition rule for mutually exclusive events.
- Work with Combinations and Permutations: For complex problems, especially those involving selecting groups or arranging items, recall the formulas for combinations C(n, r) = n! / (r! * (n – r)!) and permutations P(n, r) = n! / (n – r)!.
By following these guidelines, you can break down probability challenges into manageable steps. Remember that practice is key – the more problems you solve, the more intuitive the process becomes.
Analyzing Data with Statistical Methods
When working with data sets, it’s essential to apply the right techniques to extract meaningful insights. By using appropriate analytical methods, you can identify trends, relationships, and patterns that help inform decisions. This process involves summarizing the data, testing hypotheses, and interpreting results to draw valid conclusions.
One of the first steps in data analysis is to organize the information in a way that highlights key characteristics. Descriptive techniques, such as calculating averages and measuring variation, allow you to get an initial sense of the data’s structure. From there, more advanced methods, such as regression analysis or hypothesis testing, help explore the relationships between different variables and test potential outcomes.
Visualization tools also play a crucial role in making data more comprehensible. Graphs and charts provide a clear representation of complex relationships, making it easier to spot trends or anomalies. Whether it’s a histogram to show frequency distribution or a scatter plot to reveal correlations, effective visualization simplifies the interpretation of large data sets.
By systematically applying these approaches, you can turn raw data into actionable insights. A solid understanding of analytical methods ensures that you’re able to make informed decisions based on the patterns and trends present in the data.
Common Mistakes to Avoid in Exams

When facing a time-sensitive assessment, it’s easy to make avoidable errors that can affect your performance. Recognizing these common pitfalls and taking proactive steps to avoid them will help ensure that you maximize your potential. By being aware of these mistakes, you can approach the tasks with greater confidence and accuracy.
One frequent issue is misreading the problem. It’s essential to carefully analyze what is being asked before jumping into calculations or applying methods. Often, students make the mistake of rushing through the instructions, which can lead to applying incorrect techniques or missing critical details.
Overlooking key information is another common error. Data points or conditions mentioned in the problem may seem minor but can significantly influence the outcome. Always take time to highlight important figures and recheck them as you proceed.
Not double-checking calculations can also lead to mistakes. Even when you’re confident in your approach, simple arithmetic or transcription errors can occur. Review your steps before submitting your work to catch any miscalculations.
Finally, misunderstanding the question format can cause unnecessary confusion. Some problems may require you to provide an explanation, while others may focus on numeric solutions only. Be sure to identify the type of answer expected and tailor your response accordingly.
Avoiding these mistakes will give you the clarity and focus needed to perform at your best. Proper preparation and a thoughtful approach will help you tackle challenges with confidence and accuracy.
Breaking Down Descriptive Statistics Questions

When approaching tasks that involve summarizing and interpreting data, it’s important to break down the information into manageable parts. These types of challenges often require identifying key measures, such as averages, ranges, or distributions, and understanding their significance in the context of the problem. A step-by-step approach helps in simplifying the process and ensures that each aspect is addressed accurately.
Identifying Key Elements

Start by identifying the key components of the problem. Look for values that are essential to calculating averages, spreads, or central tendencies. These might include specific data points, sums, or even categories that help frame the analysis. Make sure you recognize whether the problem is asking for a summary measure (e.g., mean or median) or a spread (e.g., variance or range).
Calculating and Interpreting Results

Once the important elements have been identified, apply the appropriate methods for calculating each measure. For example, when finding the average, sum all values and divide by the number of data points. For range, subtract the smallest value from the largest. After computing, consider the context in which these numbers are used to understand their significance in describing the data set.
By breaking down the problem into its key parts and methodically addressing each one, you can provide clear and accurate solutions to these types of tasks. A thorough understanding of the measures and their applications will ensure that the correct approach is taken at every step.
Interpreting Statistical Graphs and Charts
Visual representations of data can reveal patterns, trends, and relationships that are difficult to identify from raw numbers alone. Understanding how to interpret these graphs and charts is essential for extracting meaningful insights. A well-designed graph can convey complex information quickly, but it’s important to know how to read the axes, labels, and scales to draw accurate conclusions.
Understanding Different Types of Graphs
Graphs come in many forms, each designed to convey different types of information. Bar charts, for example, are useful for comparing quantities across categories, while line graphs are better suited for showing trends over time. Pie charts can represent proportions within a whole, and histograms are often used to visualize frequency distributions. Familiarize yourself with the purpose of each type and how to read them effectively.
Identifying Key Insights from Visuals

Once you’ve identified the type of graph, focus on extracting the key insights. Look for trends or outliers that stand out. In line graphs, pay attention to the overall direction of the line, while in bar charts, compare the lengths of bars to identify relative magnitudes. For pie charts, examine the size of each slice in relation to the whole. Understanding these elements will help you make sense of the data and identify any significant findings.
By mastering the interpretation of visual data, you’ll be able to quickly identify important patterns and trends that inform decision-making. Practice interpreting different graphs to sharpen your skills and improve your ability to draw meaningful conclusions from visualized information.
Mastering Hypothesis Testing Techniques

Testing assumptions is a critical skill in data analysis. By evaluating whether certain claims hold true under specific conditions, you can make informed conclusions based on the available data. This process involves setting up a null hypothesis, performing calculations, and determining the likelihood that the observed results are due to chance or reflect a real effect.
One of the first steps in mastering this technique is understanding the difference between the null hypothesis and the alternative hypothesis. The null hypothesis assumes that there is no effect or difference, while the alternative hypothesis suggests the opposite. This foundational understanding will guide the choice of testing methods and the interpretation of results.
Next, it’s essential to understand how to choose the appropriate test based on the data at hand. Different tests are designed for different types of data and research questions. For example, t-tests are typically used for comparing means, while chi-square tests are used for categorical data. Mastery of these tests ensures that you apply the correct technique in each scenario.
Once the correct test is chosen, the focus shifts to calculating the test statistic and interpreting the p-value. The p-value tells you the probability of obtaining the observed results if the null hypothesis were true. If this value is lower than a pre-established significance level, you can reject the null hypothesis in favor of the alternative hypothesis.
Finally, it’s crucial to remember that hypothesis testing is not about proving a theory, but rather about assessing evidence against it. Properly applying these techniques allows for clear, evidence-based decision-making that is grounded in data.
Dealing with Regression Analysis Problems

When tackling problems involving relationships between variables, regression analysis becomes a vital tool for understanding how one factor influences another. Whether you’re working with simple linear models or more complex multivariable analyses, breaking down each component of the task will help you make sense of the data and derive meaningful insights.
Understanding the Model Setup
The first step in addressing regression-related problems is understanding the model you’re working with. Regression typically involves a dependent variable, which you are trying to predict, and one or more independent variables, which are used to explain the variation in the dependent variable. Identifying which variables belong to each category is essential for setting up the model properly.
Interpreting the Results
Once the model is set up and the calculations are performed, the next step is interpreting the results. This involves looking at key metrics, such as:
- R-squared: This tells you how well the model explains the variation in the data. A higher value indicates a better fit.
- Coefficients: These values represent the relationship between each independent variable and the dependent variable. Understanding the magnitude and direction of these coefficients is crucial for drawing meaningful conclusions.
- p-values: These help assess whether the independent variables significantly impact the dependent variable. A small p-value typically indicates a meaningful relationship.
Additionally, it’s important to check for any potential issues, such as multicollinearity or outliers, that might affect the accuracy of the analysis. By carefully evaluating these results, you can determine the strength and relevance of the relationships between variables.
Finally, keep in mind that while regression models can be powerful tools, they are not always definitive. It’s important to validate the findings by testing the model on new data or exploring alternative explanations when necessary. Proper application of regression analysis enables you to make more informed decisions based on data-driven insights.
Understanding Confidence Intervals and Errors
When analyzing data, it’s important to understand the range within which we expect true values to fall. This concept helps quantify the uncertainty inherent in estimates, offering a measure of how much trust we can place in our results. By using intervals and assessing potential errors, we can better understand the precision and reliability of our findings.
A confidence interval provides a range of values that is likely to contain the true parameter, based on a sample of data. This range is defined by a lower and upper bound, and the width of the interval depends on the variability in the data and the sample size. A wider interval suggests more uncertainty, while a narrower one indicates more precision. For instance, if we calculate a 95% confidence interval, we can say that we are 95% confident that the true value lies within this range.
On the other hand, errors refer to the difference between the observed value and the true value. These errors can be categorized into two types: systematic and random. Systematic errors consistently occur in the same direction, often due to biases or measurement inaccuracies, whereas random errors vary unpredictably from one observation to the next. Understanding these errors is essential for interpreting the results accurately and for minimizing the impact of inaccuracies in future analyses.
By mastering the concepts of confidence intervals and errors, you can more effectively interpret your results, communicate findings with greater precision, and understand the limitations of your analysis. These tools provide a framework for assessing how reliable your conclusions are, allowing for better decision-making and more informed inferences from the data.
Key Approaches to Variance and Standard Deviation

When analyzing data, two key measures of spread are frequently used to understand how much individual data points differ from the average. These measures provide insight into the level of variability within a dataset, helping to evaluate the consistency and reliability of the data. By calculating variance and standard deviation, you can determine the extent to which values deviate from the mean, which is essential for many forms of data analysis.
Variance is a measure of the average squared deviation from the mean. It quantifies the degree of spread in a dataset, with higher values indicating greater dispersion. On the other hand, standard deviation is the square root of variance, offering a more interpretable value in the same units as the data. Understanding both these measures is crucial for making accurate conclusions and for comparing different datasets.
Variance vs Standard Deviation
| Aspect | Variance | Standard Deviation |
|---|---|---|
| Definition | Average of squared differences from the mean | Square root of variance |
| Interpretability | Less intuitive, in squared units | More interpretable, in same units as data |
| Use Case | Used for determining variability in calculations | Used for easier comparison and analysis |
Both variance and standard deviation are essential for assessing the consistency of data. A low value indicates that the data points are close to the mean, while a high value suggests a greater spread of values. Understanding the relationship between these two measures helps in evaluating how data behaves and aids in making data-driven decisions more confidently.
Preparing for Multiple Choice Questions
When faced with assessments that require selecting the correct option from a list of choices, effective preparation is key to success. These types of tasks test your ability to recognize the most accurate response based on your understanding of the material. By focusing on key concepts, practicing with a variety of scenarios, and refining test-taking strategies, you can improve your ability to choose the right answer under time pressure.
Familiarity with the Material is the first step in preparation. Ensure you have a solid grasp of the core topics, as well as an understanding of the common principles and formulas that may be tested. Knowing the material inside out will help you quickly eliminate incorrect options and narrow down the choices to the most plausible ones.
Practice Makes Perfect – working through practice sets helps reinforce your knowledge and exposes you to the types of challenges you may encounter. It’s important to simulate test conditions by timing yourself, as this will help you get accustomed to working under pressure and improve your ability to pace yourself.
Critical Thinking and Elimination are vital skills when tackling these types of tasks. Start by reading each option carefully and use your knowledge to eliminate choices that are obviously incorrect. Often, even if you’re unsure about the right answer, you can increase your chances by removing clearly wrong options and focusing on the remaining choices.
Mind the Traps – many tests are designed to include tricky or misleading options. Words like “always,” “never,” or “only” are often used to identify extreme choices, which may be less likely to be correct. Being aware of these traps can help you avoid falling for them.
By combining a strong understanding of the material with strategic test-taking techniques, you can confidently approach multiple-choice tasks and improve your chances of success.
Practice Questions for Statistical Tests
To build confidence in handling various assessments that require the application of different methods, it’s essential to practice solving relevant problems. This section will guide you through a set of practical scenarios that allow you to hone your skills and apply theoretical concepts to real-world situations. Working through these examples will help you develop the critical thinking needed to successfully navigate complex tasks.
Here are some example challenges to help you improve your problem-solving abilities:
- Task 1: Given a dataset with multiple variables, determine whether the correlation between two variables is statistically significant. How would you perform the necessary calculations and what conclusions would you draw?
- Task 2: A researcher claims that the average height of adult men in a particular city is 5’10”. Conduct a hypothesis test to determine whether this claim is accurate based on a sample of 30 individuals.
- Task 3: A company wants to know if their new marketing campaign has impacted sales figures. Using a paired sample t-test, compare the pre- and post-campaign sales data to assess the effectiveness of the campaign.
- Task 4: After collecting data on a random sample of customer satisfaction scores, determine whether there is any significant difference between two product groups using an independent samples t-test.
- Task 5: Perform a chi-square test to examine if there is a relationship between customer satisfaction level and their preferred product category in a retail store.
By working through these types of challenges, you can familiarize yourself with the methods and techniques used in real-world applications. Regular practice will help you identify the appropriate test for each scenario and ensure you’re prepared to solve problems quickly and accurately when it matters most.
How to Handle Word Problems in Statistics
Word problems are often a challenge for many learners due to their detailed narratives and the need to translate real-world scenarios into mathematical solutions. These types of problems require careful reading and the ability to extract key information that can be worked with. By breaking down the problem into manageable steps, you can approach these tasks more confidently and accurately.
The first step is to identify the relevant data presented in the problem. Carefully read through the description, noting any numerical values, relationships between variables, and the specific question being asked. This will help you determine what type of method or technique is required to solve the problem.
Next, it is important to translate the word problem into a mathematical expression or formula. This could involve setting up equations, creating tables, or using known relationships between variables to guide your work. Breaking down the problem into smaller pieces often makes it easier to solve.
Another key tip is to visualize the problem. Drawing a diagram or chart can help you understand the relationships between the different elements, making it easier to apply the appropriate methods. This visual representation can be particularly helpful for problems involving distributions, trends, or comparisons.
Finally, double-check your results. Word problems can be tricky, and it’s easy to overlook small details or misinterpret the information provided. Reassessing your work ensures that your solution is logical and complete, and it can also help you catch any errors before submitting your solution.
Time Management Strategies for Statistics Exams
Effective time management is essential for success during any assessment that involves complex problem-solving. With limited time and a variety of tasks to complete, being able to allocate time efficiently can make a significant difference in achieving a higher score. By organizing your approach and sticking to a clear plan, you can ensure that each section receives the attention it requires without feeling rushed or overwhelmed.
Prioritize Tasks Based on Difficulty
Start by identifying the most challenging problems and allocate more time for them. These tasks might require deeper analysis or multiple steps, so it’s crucial to give them ample focus at the beginning. If you encounter difficulties, don’t spend too much time on a single problem. Move on to easier ones and return to the tougher problems later with a fresh perspective.
Use Time Blocks and Set Milestones
Divide the total time into blocks dedicated to specific sections or types of tasks. For example, spend a fixed amount of time on calculations, then move to theoretical or conceptual problems. Set milestones or mini-goals within these blocks to monitor your progress and ensure you’re staying on track. Regularly checking the clock will prevent you from getting too caught up in one area at the expense of others.
Remember to leave a few minutes at the end to review your work. This extra time can be crucial for catching any errors or filling in incomplete answers. A well-managed approach will reduce stress and boost your overall performance during the test.
Reviewing Past Exam Papers for Insights
Analyzing previous assessments is one of the most effective ways to understand the structure, common topics, and types of problems that are likely to appear in future tests. By going over past papers, you can familiarize yourself with the format, identify recurring themes, and refine your problem-solving skills. This approach helps to not only improve speed but also enhance accuracy during the actual test.
When reviewing past materials, focus on the following key aspects:
| Aspect | What to Look For |
|---|---|
| Common Patterns | Identify recurring topics or methods that frequently appear in past assessments. |
| Problem Types | Examine the different kinds of problems (e.g., calculations, conceptual understanding) and how they are structured. |
| Time Allocation | Observe how long it typically takes to solve different sections and practice pacing yourself accordingly. |
| Common Mistakes | Note the most common errors made by past students and work on strategies to avoid them. |
By thoroughly reviewing these elements, you can approach your next test with a clearer understanding of what to expect and how to approach each section effectively. Practicing with past materials also boosts confidence, ensuring you are better prepared when the actual assessment day arrives.