Preparing for a challenging assessment requires understanding core principles, solving complex problems, and applying learned techniques in a precise way. Whether you are looking to review essential topics or improve your problem-solving approach, mastering the material will be crucial for success.
Effective preparation involves practicing with questions that test your knowledge and ability to work under pressure. It is important to be comfortable with the format and types of problems you may encounter. By focusing on the right areas and honing your skills, you’ll be better equipped to handle whatever challenges arise.
Success in these types of assessments is not just about memorizing formulas but understanding when and how to apply them effectively. With the right approach and focused practice, you can approach your upcoming challenge with confidence and clarity.
AP Statistics Midterm Exam Guide
Achieving success in your upcoming test requires not only understanding key concepts but also practicing effective strategies for applying them under timed conditions. In this section, we will explore essential techniques to navigate through complex problems, sharpen your skills, and prepare effectively for any challenge you may face.
Understanding the Structure of the Assessment
Each test is designed to evaluate your ability to analyze data, interpret results, and solve problems using mathematical and logical reasoning. The questions typically cover a range of topics, from basic concepts to more advanced problem-solving scenarios. Familiarizing yourself with the structure of the test can significantly enhance your ability to focus on the most important areas.
Strategies for Problem Solving and Time Management
Time management is crucial. Prioritize questions based on their difficulty and your familiarity with the topic. Allocate sufficient time for more challenging problems while ensuring you can quickly complete simpler ones. Practice under timed conditions to build confidence and improve efficiency. Additionally, review the most common question types so you can quickly recognize and solve them during the test.
Understanding AP Statistics Exam Format
Familiarizing yourself with the structure of the assessment is crucial for effective preparation. Knowing the types of questions and the format in which they are presented allows you to tailor your study efforts and build confidence. In this section, we will break down the components of the test and highlight key aspects to focus on.
| Section | Description | Weight |
|---|---|---|
| Multiple Choice | Questions that test your knowledge and ability to solve problems using theoretical concepts. | 50% |
| Free Response | Open-ended problems that require you to apply multiple techniques and explain your reasoning. | 50% |
Each section requires a different approach: multiple-choice questions demand quick thinking and recognition of the correct technique, while free-response questions test your depth of understanding and ability to communicate your process clearly. By recognizing the format of each section, you can better prepare and manage your time during the test.
Key Topics Covered in the Exam
Understanding the key areas of focus in any assessment is essential for effective preparation. The questions are designed to test your ability to apply different concepts and methods, and being familiar with the core topics will help you approach the test with confidence. In this section, we will outline the primary subjects you should review before your test.
| Topic | Description |
|---|---|
| Data Interpretation | Analyzing and drawing conclusions from graphs, tables, and data sets. |
| Probability and Randomness | Understanding and calculating the likelihood of events and random phenomena. |
| Sampling and Experimentation | Designing and interpreting results from experiments and surveys. |
| Hypothesis Testing | Determining the validity of a claim based on sample data and statistical methods. |
| Confidence Intervals | Estimating a range of values for a population parameter with a specified level of certainty. |
Each of these topics plays a significant role in the overall structure of the test. A strong grasp of these areas will help you identify key patterns and solve problems more efficiently during the assessment.
How to Approach Multiple-Choice Questions
Multiple-choice questions are designed to test your ability to recognize the correct solution from a set of options. While these questions may seem straightforward, having a strategic approach can make a significant difference in your performance. Here are some helpful tips to navigate these questions effectively:
- Read the question carefully: Before looking at the answer choices, fully understand what the question is asking. Pay attention to key details and any specific instructions.
- Eliminate obvious wrong answers: Often, you can quickly rule out one or two options that are clearly incorrect. This increases your chances of selecting the correct answer from the remaining choices.
- Look for keywords: Pay attention to words like “always,” “never,” or “most likely,” as they can give clues about the accuracy of the answer.
- Double-check calculations: If the question involves calculations, make sure to check your work before finalizing your answer. This will prevent careless mistakes.
- Don’t second-guess yourself: Trust your initial instincts. Often, the first choice you eliminate and the one you select are the right answers.
By following these strategies, you can increase your accuracy and reduce the time spent on each question, allowing you to approach the rest of the test with greater confidence and efficiency.
Step-by-Step Solutions to Practice Problems
To excel in any assessment, it’s essential to practice applying your knowledge to various problems. Solving practice questions in a methodical way helps reinforce your understanding and develop critical thinking skills. In this section, we’ll walk through detailed, step-by-step solutions to common problems you may encounter, helping you build confidence and improve your problem-solving abilities.
Step 1: Understand the Problem
The first step is always to read the problem carefully and identify what is being asked. Highlight key information such as given values and what you need to solve for. It’s important to break down the problem and not rush into solving it without a clear understanding.
Step 2: Identify Relevant Formulas or Concepts
Next, think about which formulas, rules, or concepts apply to the problem. Make sure you understand the underlying principles and how they relate to the question at hand. Having a strong grasp of these concepts will help you determine the best approach for solving the problem.
Step 3: Solve the Problem
Now, proceed to solve the problem step by step. Show all of your work clearly and logically, ensuring that each step flows from the previous one. This will help you track your progress and identify where mistakes may have been made if the final answer is incorrect.
Step 4: Double-Check Your Work
Once you’ve reached an answer, go back through your steps to ensure everything is correct. Check for arithmetic mistakes, incorrect formulas, or misinterpreted information. Even small errors can lead to the wrong solution, so taking the time to review is crucial.
By practicing this structured approach, you’ll gain a better understanding of how to tackle complex problems and improve your performance in the test.
Common Pitfalls in AP Statistics Exams
While preparing for an assessment, it’s easy to overlook certain details or fall into common traps that can negatively impact your performance. Recognizing these potential pitfalls ahead of time allows you to avoid them and approach the test with greater accuracy and confidence. In this section, we will explore some of the most frequent mistakes students make and how to steer clear of them.
One common mistake is rushing through the questions without fully understanding what is being asked. This often leads to misinterpreting the problem and choosing an incorrect method to solve it. Always take the time to read the question carefully and identify key pieces of information before diving into the calculations.
Another pitfall is neglecting to check your work after completing a problem. Simple arithmetic errors or overlooking a small detail can lead to wrong answers, even if the overall approach was correct. Make it a habit to double-check each step to ensure accuracy.
Lastly, many students struggle with managing their time effectively. It’s easy to get caught up in the more difficult questions and spend too much time on them, leaving less time for easier ones. Practice balancing your time between all questions to ensure you don’t run out of time before finishing.
Tips for Time Management During the Exam
Time management is one of the most critical skills when taking a challenging test. Without a clear strategy, you may spend too much time on difficult questions and run out of time for others. In this section, we will cover effective techniques to help you manage your time efficiently and ensure you can complete all sections of the assessment.
Prioritize Your Questions
Start by quickly scanning the entire set of questions to get a sense of what to expect. Identify any questions that seem particularly easy or familiar, and tackle those first. This will boost your confidence and ensure you accumulate points quickly. Save the more difficult or time-consuming problems for later, when you can dedicate more time to them.
Allocate Time for Each Section
Before you start the test, divide your available time by the number of sections or questions. Set specific time limits for each section, and stick to them. If you spend too much time on one part, move on and come back to it later if needed. Managing time for each section ensures you don’t get stuck on one question and leaves you with enough time to finish the entire test.
By planning ahead and staying mindful of the clock, you can reduce stress and complete the test to the best of your ability.
Reviewing Key Formulas for AP Statistics

Mastering essential formulas is crucial for solving problems accurately and efficiently. These mathematical expressions serve as the foundation for much of the test and are vital tools for interpreting data and making predictions. In this section, we will review some of the most important formulas you should be familiar with and how they are applied in different contexts.
Mean Formula: The mean, or average, is calculated by summing all data points and dividing by the number of data points. The formula is:
Mean = (ΣX) / N
Where ΣX represents the sum of all data points and N is the total number of data points.
Standard Deviation Formula: The standard deviation measures the spread of data points from the mean. The formula is:
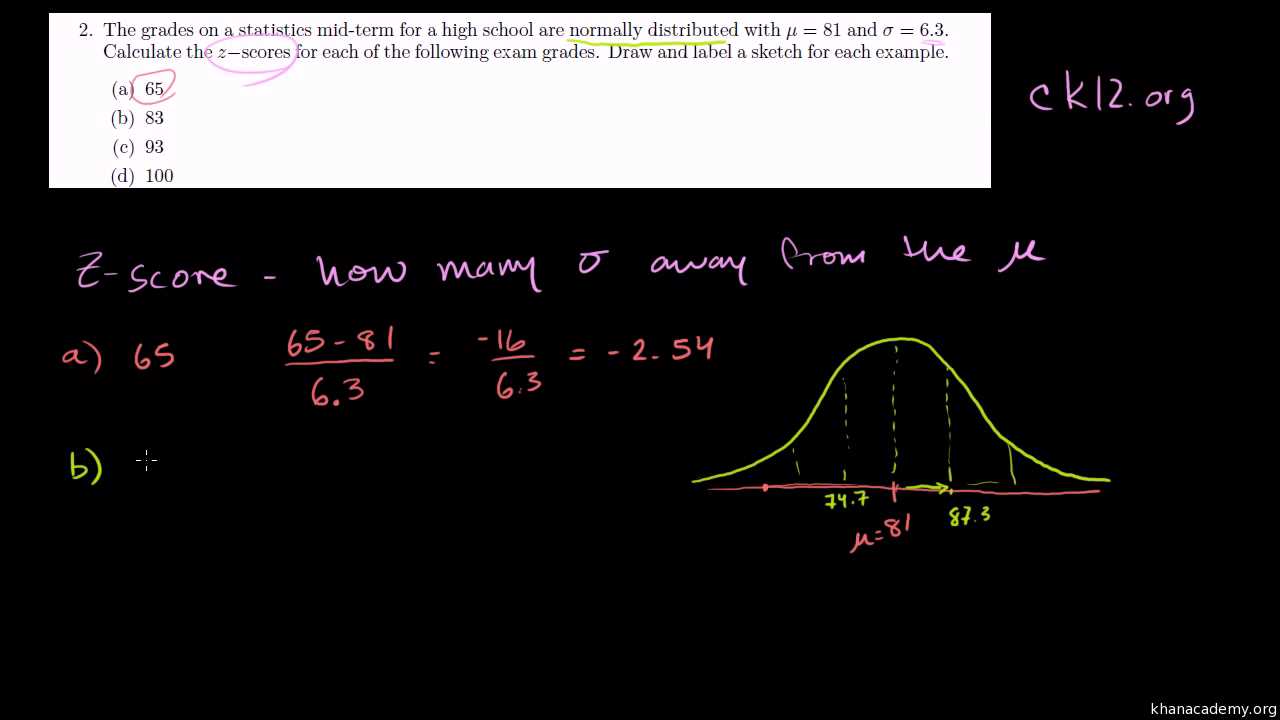
σ = √(Σ(X – μ)² / N)
Where σ is the standard deviation, μ is the mean, X represents each data point, and N is the total number of data points.
Probability Formula: The probability of an event occurring is given by the ratio of the number of successful outcomes to the total number of possible outcomes. The formula is:
P(A) = Number of favorable outcomes / Total number of possible outcomes
By regularly reviewing these formulas and understanding their applications, you’ll be well-prepared to tackle a wide variety of questions that require mathematical computation and data analysis.
How to Interpret Statistical Data Effectively
Interpreting data correctly is crucial for drawing meaningful conclusions and making informed decisions. Whether you’re dealing with raw numbers, charts, or graphs, the ability to understand the underlying patterns and trends can help you solve problems and answer questions accurately. This section will guide you through some key strategies for interpreting data effectively.
The first step in interpreting data is to understand the context in which it was collected. This includes knowing what the data represents, how it was gathered, and what its limitations might be. Without this understanding, you might misinterpret results or draw incorrect conclusions.
Next, focus on identifying trends and patterns within the data. Look for significant outliers, groupings, or relationships that can provide insights. Pay close attention to how data points are distributed, as this can help you understand the spread and central tendency of the dataset.
When analyzing visual representations like charts or graphs, be sure to examine the axes, labels, and scales carefully. A well-designed graph should highlight the key information, while a poorly designed one can lead to confusion or misinterpretation.
Finally, always be cautious when making inferences based on the data. Ensure that any conclusions drawn are supported by the evidence, and consider alternative explanations for the trends you observe. This critical thinking approach will help you interpret data more accurately and confidently.
Importance of Hypothesis Testing in Exams
Hypothesis testing is a powerful method for evaluating assumptions and drawing conclusions based on data. In the context of assessments, it plays a critical role in determining whether a specific claim or theory is supported by the available evidence. Understanding the process of hypothesis testing is essential for successfully navigating questions that require analytical reasoning and data interpretation.
Building a Strong Foundation
At the core of hypothesis testing is the ability to make informed decisions about the validity of a claim. It allows you to test whether observed patterns in data are due to chance or if they suggest a real underlying effect. This is especially important in scenarios where you need to analyze trends, relationships, or differences between groups.
Application in Decision Making
In many cases, hypothesis testing involves two competing hypotheses: the null hypothesis (which assumes no effect or no difference) and the alternative hypothesis (which suggests an effect or difference exists). By using data to evaluate these hypotheses, you can make objective decisions based on evidence rather than assumptions or bias. This process is valuable not only in exams but also in real-world situations where accurate conclusions are required.
Key Benefits:
- Helps identify statistically significant findings
- Promotes critical thinking and data-driven conclusions
- Supports logical decision-making in uncertain situations
Mastering the principles of hypothesis testing allows you to approach questions with confidence and make well-supported decisions during assessments.
Calculating Confidence Intervals Correctly
Calculating confidence intervals is an essential technique for estimating the range within which a population parameter likely lies. It provides a level of certainty about the results obtained from sample data and allows for informed decision-making. This section outlines the correct process for calculating and interpreting confidence intervals, ensuring accuracy in your analysis.
The first step in calculating a confidence interval is to identify the sample statistic, such as the sample mean or proportion. This value represents the best estimate of the population parameter. From here, you can calculate the margin of error, which accounts for the uncertainty inherent in working with sample data.
Steps for Calculating a Confidence Interval:
- Determine the sample statistic (mean, proportion, etc.).
- Find the critical value, often based on a z-score or t-score, depending on the sample size and distribution.
- Calculate the standard error, which measures the variability of the sample statistic.
- Multiply the critical value by the standard error to find the margin of error.
- Add and subtract the margin of error from the sample statistic to get the lower and upper bounds of the confidence interval.
Example: If the sample mean is 50, the margin of error is 5, and the confidence level is 95%, the confidence interval would be from 45 to 55. This means that we are 95% confident that the true population mean lies within this range.
By following these steps, you can confidently calculate and interpret the interval, ensuring that your conclusions are based on accurate and reliable data.
Understanding the Central Limit Theorem
The Central Limit Theorem (CLT) is a fundamental concept that explains how the distribution of sample means approaches a normal distribution as the sample size increases, regardless of the shape of the original population distribution. This powerful theorem is crucial for making inferences and drawing conclusions based on sample data.
Key Principles of the CLT
The CLT asserts that when you take large enough random samples from a population, the distribution of the sample means will be approximately normal, even if the population itself is not normally distributed. The larger the sample size, the closer the sample mean distribution will be to a normal distribution, which makes it easier to apply statistical methods that assume normality.
Applications of the CLT
Understanding the CLT is essential because it allows for the use of normal distribution properties in many statistical procedures. For example, it is widely used in hypothesis testing, confidence intervals, and estimating population parameters. By leveraging the CLT, you can make accurate predictions and assess the reliability of your findings, even when you are working with non-normal data.
In summary, the Central Limit Theorem provides a bridge between sample data and the broader population, making it a cornerstone of inferential statistics. By understanding its application, you can gain deeper insights into how sample data behaves and make more informed decisions based on that data.
How to Tackle Probability-Based Questions
Probability questions require a solid understanding of chance and uncertainty. These questions often involve calculating the likelihood of certain events or outcomes occurring, and being methodical in your approach is key to solving them correctly. Whether you’re working with simple events or more complex scenarios, following a structured process can help you navigate these questions with confidence.
Steps to Approach Probability Problems
To tackle probability-based problems effectively, follow these steps:
- Understand the problem: Read the question carefully to identify the events or outcomes in question. Determine whether the problem involves independent or dependent events, or if it requires conditional probability.
- List all possible outcomes: For many probability problems, creating a list or table of all possible outcomes (sample space) can help clarify the situation.
- Determine the favorable outcomes: Identify which outcomes align with the event you’re calculating the probability for.
- Use the appropriate formula: Depending on the problem, apply the correct probability formula. For example, use the basic formula of probability: P(A) = Number of favorable outcomes / Total number of outcomes.
- Check for special conditions: Watch for special conditions like “with replacement” or “without replacement” in problems involving draws or selections, as these impact the calculation.
Common Probability Concepts to Remember
Here are a few key concepts to keep in mind when working with probability problems:
- Independent Events: Events that do not affect each other’s outcomes (e.g., flipping a coin multiple times).
- Dependent Events: Events where the outcome of one affects the outcome of another (e.g., drawing cards from a deck without replacement).
- Complementary Events: The probability of an event not occurring is 1 minus the probability of it occurring (P(not A) = 1 – P(A)).
- Conditional Probability: The probability of an event occurring given that another event has already occurred.
By approaching probability questions systematically and keeping these key concepts in mind, you can solve even the most challenging problems with ease. Remember, practice is essential–the more you work with probability, the more intuitive it will become.
Real-World Applications in Statistics Problems
Understanding how theoretical concepts are applied to real-world scenarios is an essential part of learning. When studying how data is collected, interpreted, and used to make decisions, it’s important to recognize the practical applications that these methods have in everyday life. Whether it’s in business, healthcare, or social sciences, the ability to apply data analysis tools effectively can lead to informed decision-making and valuable insights.
Examples of Real-World Uses
Here are some of the fields where data analysis plays a critical role:
| Field | Application | Impact |
|---|---|---|
| Healthcare | Medical research, clinical trials, patient outcomes | Helps improve treatments, predict disease trends, and optimize healthcare resources |
| Marketing | Consumer behavior analysis, targeted advertising | Enables businesses to optimize product offerings and target the right audience |
| Finance | Risk assessment, investment strategies | Supports better decision-making for investments, loans, and market strategies |
| Government | Public policy decisions, census data | Guides effective resource allocation and informs policy decisions |
| Sports | Performance analysis, team strategy | Improves training methods, game tactics, and player performance |
Analyzing Data for Real-World Solutions
Applying data analysis tools to these fields often involves collecting large sets of data, interpreting it, and drawing conclusions to guide decision-making. Whether it’s through regression analysis, hypothesis testing, or probability modeling, these techniques provide crucial insights that can lead to optimized solutions and improved outcomes in various sectors.
By exploring these real-world applications, you can better understand the importance of mastering data analysis techniques. Not only does this knowledge help you perform well in academic settings, but it also prepares you for solving practical problems in a wide range of industries.
Best Study Resources for AP Statistics

When preparing for a challenging academic test, the right study materials can make all the difference. Whether you’re reviewing concepts, practicing problems, or seeking expert guidance, having access to reliable resources can boost your understanding and performance. Below are some of the top study tools that can help you excel in mastering data analysis methods and related topics.
Top Books and Guides
Books and study guides are an essential part of any exam preparation. Below are some popular choices:
- 5 Steps to a 5: AP Statistics – A comprehensive guide that provides practice exams, detailed explanations, and study plans.
- Cracking the AP: Statistics – Offers tips, strategies, and practice questions for a deeper understanding of key concepts.
- Barron’s AP Statistics – Known for its clear explanations and in-depth practice questions, this book is a staple for many students.
Online Learning Platforms
Utilizing online platforms can offer a more interactive approach to learning. Some great options include:
- Khan Academy – Provides free video tutorials and practice exercises on a wide range of topics, including data analysis.
- AP Classroom – Offers official materials from the College Board, including practice questions and resources tailored to the test format.
- Quizlet – A flashcard-based learning platform where you can find user-created sets for reviewing key terms and formulas.
These resources offer a mix of visual aids, structured lessons, and practice exercises that can enhance your preparation and increase your confidence when approaching the subject.
How to Stay Calm During the Exam
Test anxiety is a common challenge that many students face. The pressure to perform well can cause stress, but it’s important to remember that staying calm and focused can help you succeed. Developing strategies to manage your emotions and maintain composure is key to navigating the test effectively.
Breathing and Relaxation Techniques
One of the most effective ways to manage stress is through controlled breathing. Deep breaths can help calm your nervous system, lowering your heart rate and clearing your mind. Here are some techniques you can use:
- Deep Breathing: Inhale slowly through your nose for a count of four, hold for four seconds, and then exhale through your mouth for a count of four. Repeat this process to relax.
- Progressive Muscle Relaxation: Tense and then relax each muscle group, starting from your feet and working your way up to your head. This can release tension and promote relaxation.
Time Management and Pacing Yourself
Managing your time during the test is crucial to avoid feeling overwhelmed. Start by assessing the length and complexity of each section. Allocate time for each part and stick to your plan. If you get stuck on a difficult question, move on and return to it later, ensuring you don’t waste precious time.
- Divide Your Time: Set specific time limits for each section or set of questions to ensure you can complete the entire test.
- Stay Flexible: If a question seems too difficult, mark it and continue with the other questions. This helps maintain momentum and reduces stress.
By incorporating these strategies, you can stay calm and focused, giving yourself the best chance to perform well and manage your stress levels effectively throughout the test.
Post-Exam Review and Improvement Tips
After completing any major assessment, it’s essential to take the time to reflect on your performance. Reviewing your work thoroughly can highlight areas where you did well and identify parts that need more attention. This process helps you understand your mistakes, learn from them, and prepare better for future challenges.
One of the most important aspects of post-assessment reflection is analyzing the types of questions that caused difficulty. Were there certain topics that you found confusing or time-consuming? Were there any patterns in your errors that could indicate gaps in your understanding? Identifying these areas will allow you to focus your future studies on improving in those specific areas.
Analyzing Mistakes
It’s crucial not only to understand what mistakes you made but also to recognize why they happened. Were they due to misunderstanding the question, miscalculating, or rushing through the material? Here’s how you can approach this analysis:
- Review Incorrect Questions: Look at each question you answered incorrectly and try to identify the exact mistake.
- Understand the Concept: If you missed a question due to a misunderstanding of the concept, revisit your notes or textbooks to clarify your knowledge.
- Practice Similar Problems: Reinforce your learning by practicing problems related to the ones you got wrong. This repetition will help solidify your understanding.
Setting Goals for Improvement
Once you’ve identified your weak areas, it’s time to set clear goals for improvement. This will give you direction and motivation as you continue your studies. Consider the following tips:
- Create a Study Plan: Break down the topics that need improvement into manageable sections and set a timeline for studying them.
- Seek Additional Resources: Utilize textbooks, online tutorials, and study groups to further your understanding of challenging concepts.
- Practice Under Timed Conditions: Simulate the test environment by practicing under time constraints. This will help you become more efficient and less anxious during future assessments.
By reviewing your performance thoroughly and taking proactive steps to address your weak areas, you can improve your skills and approach future assessments with greater confidence and success.