
Understanding how to calculate and analyze three-dimensional objects is essential for students and professionals alike. The ability to accurately measure and interpret the size of various shapes plays a crucial role in fields ranging from architecture to engineering and beyond. By practicing these skills, you can strengthen your understanding of spatial relationships and enhance your problem-solving abilities.
In this section, we explore effective methods for solving problems related to determining the size, capacity, or amount of space within different objects. Whether you are working with regular shapes or irregular forms, mastering these techniques will help you navigate complex questions with ease. With a clear grasp of the core principles, you will be equipped to tackle a wide variety of practical challenges.
Developing a strong foundation in these concepts can lead to more efficient calculations and a deeper understanding of how these principles apply to real-world scenarios. Let’s dive into the most effective ways to approach these problems and solve them step by step, ensuring you gain both confidence and expertise.
Volume Review Worksheet Answers

Mastering the calculation of three-dimensional objects requires understanding key principles and applying specific methods. The process of solving such problems often involves multiple steps, each contributing to a more accurate interpretation of an object’s size and capacity. This section provides insight into how to approach these tasks effectively, breaking down each step for clearer understanding and faster problem-solving.
To begin, it’s important to familiarize yourself with the basic concepts and the formulas used to calculate the size or space within an object. Once you are comfortable with the principles, you can apply them systematically to various shapes and figures.
Here are the key steps to follow when tackling these types of problems:
- Identify the shape and structure of the object being measured.
- Determine the relevant formula for that shape (e.g., for cubes, rectangular prisms, spheres, etc.).
- Insert the known values into the formula.
- Perform the necessary calculations carefully.
- Verify the result to ensure consistency and accuracy.
By following these steps, you will improve your problem-solving approach, reducing errors and gaining a better understanding of the spatial properties of various objects. It’s essential to practice these techniques regularly, as repetition will help solidify your ability to quickly solve similar problems in the future.
Additionally, when solving such problems, it’s beneficial to break down complex figures into simpler components. This allows you to use basic formulas on individual parts before combining them for a comprehensive result. Below are a few practical examples:
- For a composite object consisting of a cylinder and a cone, calculate each part’s capacity separately and add them together.
- If dealing with irregular shapes, consider dividing them into smaller, recognizable components to simplify the calculation process.
Through consistent practice and a strategic approach, you will become proficient in calculating the capacity and size of three-dimensional objects, improving both your efficiency and accuracy in problem-solving tasks.
Understanding the Basics of Volume
When measuring the amount of space within three-dimensional objects, it’s essential to understand the fundamental principles behind these calculations. This concept plays a critical role in various real-world applications, from determining the capacity of containers to calculating the amount of material needed for construction projects. To accurately determine the internal size of an object, specific formulas and methods are required.
The process typically begins by identifying the shape or structure of the object. Each type of object, whether it’s a cube, sphere, cylinder, or irregular form, has its own unique way to calculate its internal space. Understanding these differences is key to making accurate measurements and solving related problems.
Once the shape is recognized, the next step is to apply the correct formula, inserting known values such as length, width, height, or radius, depending on the object. The result will provide the total internal space, helping to quantify how much can be held or contained within the given shape.
In summary, the basics of this topic involve recognizing the shape, using the correct formula, and applying the proper values to accurately calculate the internal capacity. Mastering these principles is crucial for solving complex spatial problems and gaining a deeper understanding of how objects occupy space in the physical world.
How to Solve Volume Problems
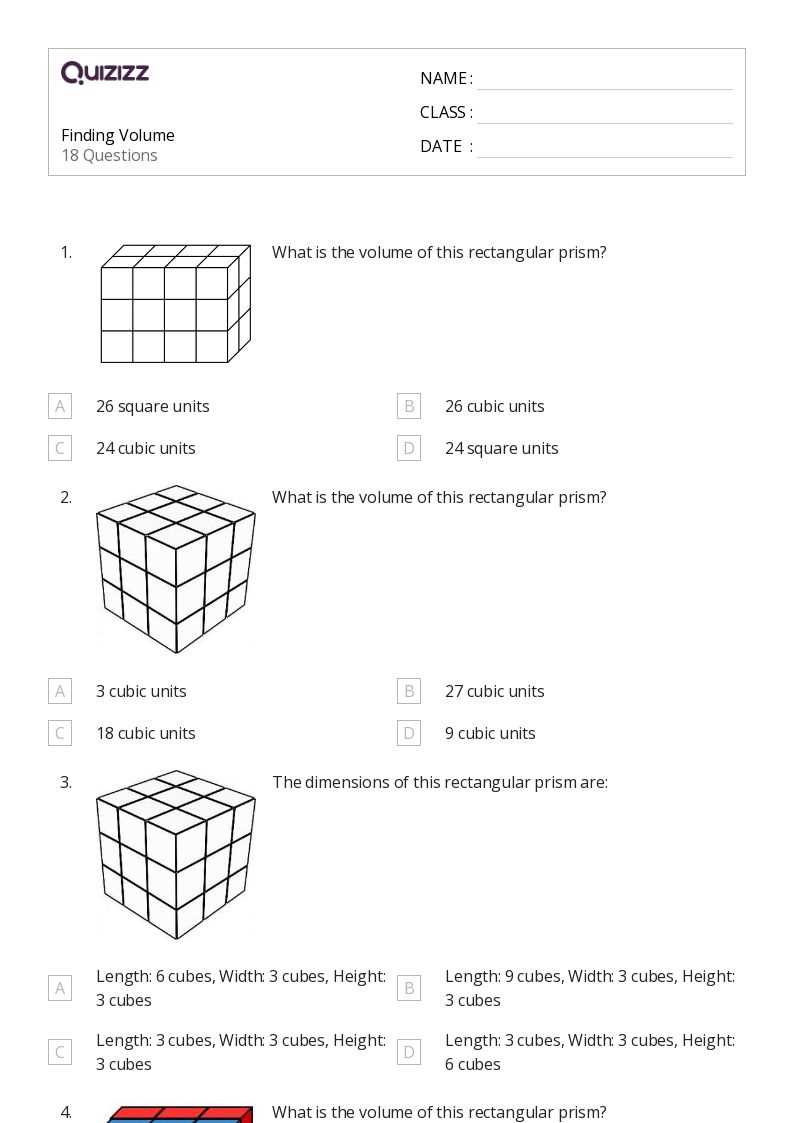
Solving problems related to determining the amount of space inside an object requires a systematic approach. These tasks often involve applying formulas, understanding measurements, and carefully following a series of logical steps. Whether working with basic geometric shapes or complex figures, the goal is to find the correct method to determine the internal capacity of the object in question.
Step-by-Step Approach
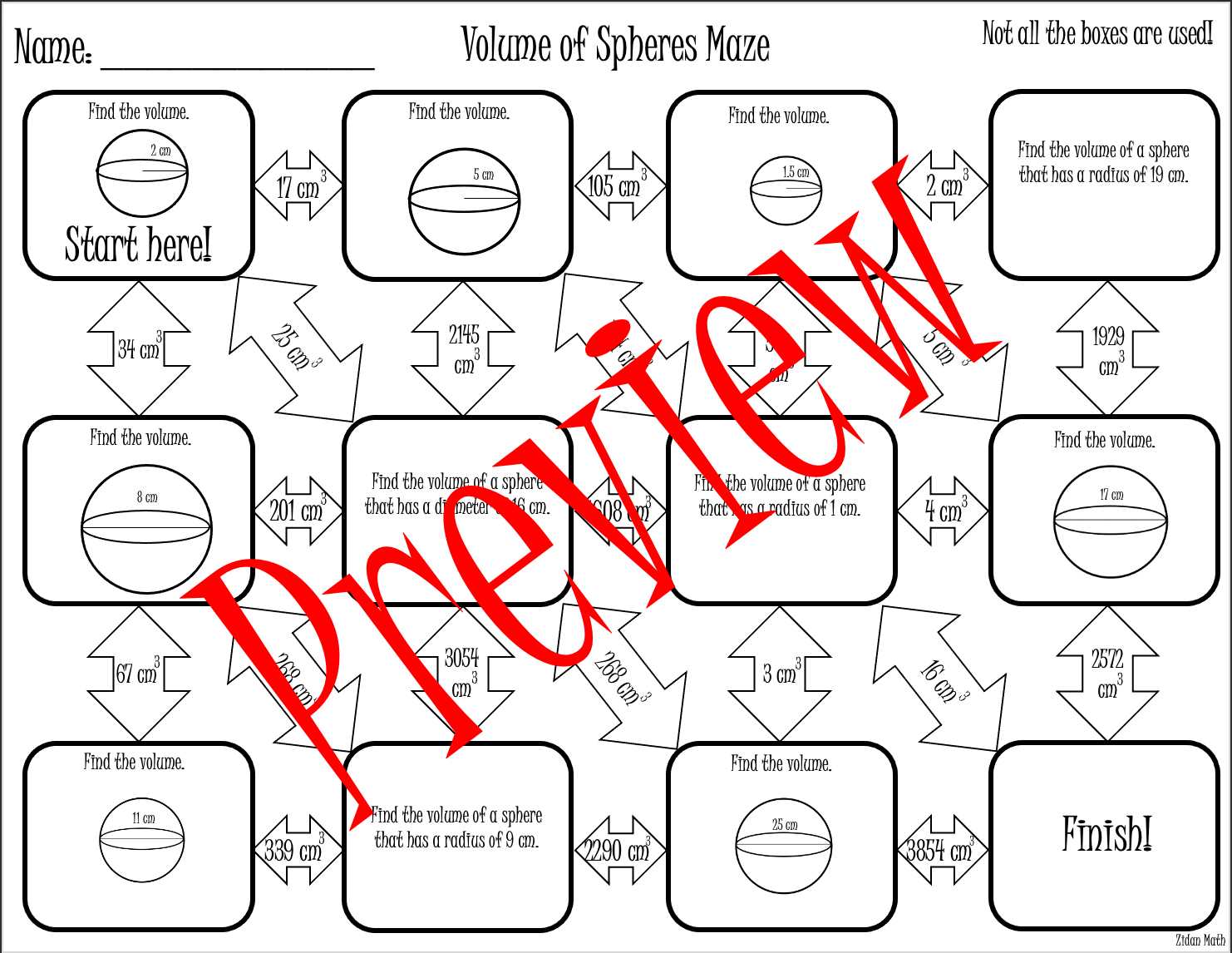
To solve these types of problems, follow these steps:
- Identify the object’s shape: Determine whether you are working with a cube, sphere, cylinder, cone, or any other geometric figure.
- Select the appropriate formula: Each shape has its own formula, so it’s crucial to know which one to use. For example, a cube requires the formula for cubic measurements, while a cylinder involves calculations for circular bases and height.
- Insert the given values: Place the known dimensions into the chosen formula. These could be measurements like radius, height, or length.
- Perform the calculations: Carry out the mathematical operations carefully. Pay attention to units of measurement and ensure that they are consistent throughout.
- Check your result: Verify that the answer makes sense in the context of the problem and double-check your calculations for accuracy.
Tips for Efficient Problem Solving
To improve your speed and accuracy, here are a few helpful tips:
- Break down complex shapes into simpler components, solving each part separately and then combining the results.
- Always double-check your formula before proceeding with the calculations.
- Keep track of units, ensuring all measurements are in the same system (e.g., inches, centimeters). If necessary, convert them before calculating.
- Practice with various types of problems to become familiar with different formulas and techniques.
By following these steps and tips, you will develop a deeper understanding of how to approach and solve problems related to the space and capacity of objects. With practice, you’ll be able to tackle even the most complex challenges with confidence.
Common Mistakes in Volume Calculations
When calculating the internal space of objects, many individuals encounter errors that can lead to inaccurate results. These mistakes often arise from misunderstandings of formulas, incorrect measurements, or simple calculation oversights. Recognizing and addressing these common pitfalls can significantly improve the accuracy and reliability of your results.
One frequent mistake is misidentifying the appropriate formula for a given shape. Each figure–whether it’s a cylinder, cube, or cone–has a unique way to determine its internal capacity. Using the wrong formula, or failing to adapt the formula correctly for specific circumstances, can lead to significant errors.
Another common issue involves confusion with units of measurement. Failing to convert units properly or mixing units (e.g., using centimeters for one dimension and meters for another) can distort the final result. It’s crucial to ensure all measurements are in the same unit system before applying them to the formula.
Additionally, neglecting to check the result can be a costly mistake. Sometimes, even after performing the correct steps, errors in arithmetic can go unnoticed. Always recheck your calculations to confirm accuracy and prevent simple mistakes from affecting your outcome.
Lastly, for more complex objects, forgetting to break down the figure into simpler parts can lead to missed components. For example, if the object is a composite shape, failing to treat it as separate geometric figures before combining their results can cause incorrect measurements.
Avoiding these common mistakes requires careful attention to detail, understanding the formulas, and verifying each step before reaching a conclusion. With practice, you can minimize these errors and achieve more precise results in your calculations.
Key Formulas for Volume Worksheets
To accurately calculate the space occupied by three-dimensional objects, it’s essential to understand and apply the correct formulas. Each shape has its own unique method for determining its internal capacity, and knowing these key equations is crucial for solving related problems effectively. Below are some of the most commonly used formulas for various shapes.
Cylinder: For a cylinder, the formula is based on the area of its circular base and its height. The equation is:
Area = π × r² × h
Where r is the radius of the base, h is the height, and π is approximately 3.14159.
Cube: For a cube, all sides are of equal length. The formula for its internal space is:
Area = s³
Where s is the length of one side of the cube.
Rectangular Prism: A rectangular prism is a shape with six rectangular faces. To calculate its internal capacity, the formula is:
Area = l × w × h
Where l is the length, w is the width, and h is the height.
Sphere: To calculate the space within a sphere, use the formula:
Area = (4/3) × π × r³
Where r is the radius of the sphere.
Cone: For a cone, the formula is similar to that of a cylinder but includes a fraction to account for the conical shape:
Area = (1/3) × π × r² × h
Where r is the radius of the base and h is the height.
Understanding these formulas and how to apply them is vital for accurately calculating the internal space of various objects. By mastering these equations, you can confidently solve complex problems and ensure your measurements are precise.
Tips for Efficient Volume Solving
When tackling problems related to determining the internal space of objects, efficiency can save both time and reduce the chances of making errors. By adopting certain strategies, you can streamline your problem-solving process and increase your accuracy. Below are some helpful tips for solving these types of problems more effectively.
Organize Your Approach
Having a clear plan before starting the calculations is key to solving problems efficiently. Begin by carefully analyzing the shape in question. Identify its dimensions and the relevant formula to use. Organizing your steps ahead of time allows you to avoid unnecessary mistakes and ensures you don’t miss any critical components.
- Identify the Shape: Whether it’s a cube, cylinder, or irregular shape, know what you’re dealing with before applying a formula.
- Use the Correct Formula: Be sure to apply the right equation for the shape you are working with to avoid miscalculations.
- Check Units: Always ensure that all your measurements are in the same unit system to prevent errors from unit conversion.
Utilize Time-Saving Strategies
There are several strategies you can use to speed up the process without sacrificing accuracy:
- Work with Simplified Components: For complex shapes, break them into simpler forms, calculate each part individually, and then combine the results.
- Double-Check Your Work: A quick review of your calculations can help catch simple arithmetic mistakes.
- Practice Regularly: The more you practice, the faster and more confident you will become with the steps and formulas.
By organizing your approach, selecting the right strategies, and practicing consistently, you’ll not only increase your solving speed but also improve the precision of your results. These tips can help you efficiently tackle even the most challenging problems with ease.
Breaking Down Complex Volume Questions
When confronted with intricate problems involving the internal capacity of objects, it’s important to approach them systematically. Breaking down these challenges into manageable steps can help simplify complex scenarios. Often, large or irregularly shaped objects require a thoughtful approach to separate the problem into smaller, more straightforward components that can be solved individually.
Step-by-Step Breakdown
To tackle a complicated question, follow these steps:
- Identify all components: Look for different parts within the object that may have distinct shapes. These might be simple geometric figures like cubes or cylinders, or more complex forms.
- Break the object into simpler parts: If the shape is irregular, divide it into basic shapes, such as rectangles, spheres, or cones, for which you already know the formulas.
- Calculate the space for each part: Apply the appropriate formula to each of the individual components. This ensures that no part of the object is overlooked.
- Sum the results: Once all parts are calculated, add them together to find the total internal capacity.
Common Pitfalls to Avoid
While breaking down complex shapes, there are a few common issues to watch for:
- Forgetting to account for all parts: Ensure that no component, no matter how small, is left out in your calculations.
- Incorrectly combining shapes: When adding results from different parts, double-check that the dimensions are consistent, particularly when dealing with different units.
- Using the wrong formula: Make sure to select the correct formula for each component. For example, a cylinder requires a different equation than a sphere.
By breaking down complex questions into smaller, simpler steps and being cautious of potential errors, you can confidently solve even the most challenging problems. With practice, this approach will help you become more efficient and accurate in handling intricate scenarios.
Real-World Applications of Volume Calculations
Understanding the internal space of objects is crucial in many fields, from engineering to everyday problem-solving. Accurate measurements of a structure’s capacity are used in various real-world scenarios to ensure functionality, safety, and efficiency. By applying these concepts, professionals and individuals can make informed decisions in areas such as construction, manufacturing, and even environmental science.
Construction and Architecture
In construction, calculating the space inside a building or structure is essential for planning, design, and material estimation. Architects and engineers use these measurements to determine the volume of rooms, halls, and other spaces. This is especially important when calculating heating, ventilation, and air conditioning (HVAC) systems or determining the amount of concrete needed for foundations and walls.
- Estimating building materials: Knowing the required amount of concrete, paint, or insulation involves calculating the internal space of different sections of the structure.
- HVAC design: Proper airflow and temperature control depend on the accurate calculation of a room’s volume to determine the capacity of the systems needed.
Manufacturing and Packaging

In manufacturing, precise calculations of the internal space of containers, tanks, or machinery are essential for efficiency and cost-effectiveness. For example, packaging companies use these calculations to design boxes and containers that fit products perfectly, minimizing wasted space and reducing shipping costs.
- Packaging design: Accurate measurements ensure that products are packed securely and efficiently, reducing material waste and maximizing storage.
- Tank capacity: Calculating the volume of storage tanks, pipes, or vats is critical for industries like food production, pharmaceuticals, and chemical engineering.
Environmental Science and Ecology
In environmental science, calculating the capacity of natural and man-made reservoirs, such as lakes, dams, and aquifers, helps in managing water resources. By understanding the space occupied by water in these systems, researchers can assess water supply, flood risks, and the impact of environmental changes on ecosystems.
- Water resource management: Accurate measurements of reservoirs are necessary for ensuring the sustainability of water supplies in agriculture, industry, and urban areas.
- Flood prediction: Calculating the capacity of rivers and lakes helps predict the likelihood of flooding in specific regions during heavy rainfall.
These real-world applications demonstrate how essential accurate space calculations are across various fields. Whether it’s for designing buildings, creating efficient packaging, or managing natural resources, understanding how to calculate internal capacity is key to making informed, effective decisions.
Volume Units and Conversions Explained
When dealing with measurements related to the internal capacity of objects, it’s crucial to understand the different units used to quantify space. Whether you’re working with small containers or large tanks, knowing how to convert between different units ensures accuracy in your calculations. This section will clarify common units of measurement and explain how to convert between them effectively.
Common Units of Measurement

There are several units used to measure the amount of space inside an object. The choice of unit often depends on the scale of the object and the context in which the measurement is being made.
- Cubic meters (m³): This is the standard unit for larger volumes, commonly used in construction, shipping, and environmental science.
- Liters (L): Often used for liquids or smaller spaces, such as in beverage containers, cooking, or pharmaceuticals.
- Cubic centimeters (cm³): A unit typically used for small-scale measurements, like the internal capacity of a car engine or a small box.
- Cubic inches (in³): Common in the United States for measuring the internal space of smaller objects or containers, especially in industries like packaging.
Unit Conversions
To ensure accurate calculations, it’s important to know how to convert between different units. For example, converting from cubic meters to liters or from cubic inches to cubic centimeters may be necessary depending on the task at hand.
- 1 cubic meter (m³) = 1,000 liters (L)
- 1 liter (L) = 1,000 cubic centimeters (cm³)
- 1 cubic inch (in³) = 16.387 cubic centimeters (cm³)
- 1 cubic foot (ft³) = 28.317 liters (L)
By mastering these units and conversion formulas, you can work confidently with measurements, ensuring accuracy and consistency in your calculations. Whether you’re calculating the capacity of a swimming pool or determining the right container for shipping goods, understanding how to convert between units is a fundamental skill.
Practice Problems for Mastering Volume
Practicing with a variety of problems is one of the best ways to solidify your understanding of space calculations. By applying the concepts to different scenarios, you can improve your problem-solving skills and gain confidence in handling both simple and complex situations. In this section, we’ll present several practice problems designed to challenge and strengthen your abilities.
Simple Shapes
Start with basic shapes to build a strong foundation. These problems will help you understand the core principles and formulas for calculating internal capacity in common objects.
- Problem 1: Calculate the capacity of a box with dimensions 4m by 3m by 2m.
- Problem 2: Find the internal space of a cylinder with a radius of 5cm and a height of 10cm.
- Problem 3: A sphere has a radius of 7 inches. What is its total space?
Complex Structures
Once you’ve mastered basic shapes, move on to more complicated forms that require breaking down the object into multiple parts. These problems will challenge your ability to apply multiple formulas and handle irregular measurements.
- Problem 4: A swimming pool has a rectangular base of 8m by 5m and a semi-circular end with a radius of 3m. What is the total space?
- Problem 5: A cone with a base radius of 6cm and a height of 12cm is attached to a cylindrical tank with a radius of 6cm and a height of 8cm. What is the total capacity of this combined shape?
Working through these practice problems will help you apply what you’ve learned and build a deeper understanding of how to calculate the internal space of different objects. By progressing from simple shapes to more complex ones, you’ll be prepared for any real-world scenario that requires these calculations.
How to Check Your Volume Answers
Verifying your calculations is an essential step in ensuring the accuracy of your results. Whether you are solving simple or complex problems, knowing how to check your work helps avoid errors and strengthens your understanding. This section outlines the best strategies to confirm that your calculations are correct.
Step-by-Step Verification
Start by reviewing each part of the problem. Make sure you understand the dimensions and the correct formula needed for each calculation. It’s also helpful to compare your result with a rough estimate to see if the value seems reasonable.
- Double-check units: Ensure that all units are consistent throughout the problem.
- Revisit formulas: Confirm that you’ve used the correct formula for each object’s shape.
- Cross-check with common values: For familiar objects, like a sphere or a box, verify that your result is in the expected range based on real-world examples.
Using a Table for Comparison
One effective method for validating your results is using a comparison table. After performing the calculations, you can compare your solution with standard values for similar problems. Below is an example of a table you can use for verification.
| Shape | Calculated Result | Expected Range |
|---|---|---|
| Cube (5m side) | 125 m³ | 100 – 130 m³ |
| Cylinder (5cm radius, 10cm height) | 785.4 cm³ | 780 – 800 cm³ |
| Sphere (7 inches radius) | 1436.8 in³ | 1400 – 1450 in³ |
By following these steps and using comparison methods, you can ensure that your results are accurate. Consistently checking your work will not only prevent mistakes but also build confidence in your calculation skills.
Importance of Accurate Volume Measurements
Precise calculations of internal capacity play a crucial role in various fields, from construction to scientific research. Whether you’re designing an object, determining the required space for materials, or analyzing physical properties, getting the right measurements is essential. Inaccurate results can lead to costly mistakes, inefficiencies, and even safety concerns.
Correctly determining the amount of space inside a given shape ensures that designs function as intended. In industries like manufacturing, engineering, and architecture, miscalculating can result in wasted resources or improper fit. Even small errors can compound over time, causing larger discrepancies in the final outcome.
Moreover, having reliable measurements is key to making informed decisions. It allows for proper material estimation, optimization of resources, and compliance with regulations. Whether calculating for practical applications or academic purposes, understanding the significance of precision in these calculations is vital for success in any related task.
Solution Walkthrough for Capacity Calculations
Understanding how to tackle capacity problems step by step is crucial for mastering these types of exercises. In this section, we’ll walk through a typical example, breaking down each stage of the process. This approach will help you better understand how to apply the appropriate formulas and avoid common mistakes when determining internal space or content volume.
Step 1: Identify the Object and Formula

The first step in solving these types of problems is identifying the object you are dealing with. Whether it’s a sphere, cylinder, or cube, each shape has its own formula for calculating capacity. For instance, for a cube, the formula is the side length cubed. For a cylinder, you’ll need to use the area of the base multiplied by the height. Once you know the shape, make sure you have the correct formula at hand.
Step 2: Substitute Values and Solve
After selecting the correct formula, the next step is substituting the known values (like length, width, radius, etc.) into the equation. Take care to convert any units if necessary, as consistency is key in accurate calculations. Once all the values are in place, perform the necessary arithmetic steps to find the result.
- For a cube: Multiply the side length by itself three times.
- For a cylinder: Multiply the area of the base (πr²) by the height.
- For a sphere: Use the formula (4/3)πr³ to find the internal capacity.
As we proceed through these steps, remember that double-checking the input values and units is critical to avoid small errors that can lead to incorrect results.
Strategies for Fast Capacity Problem Solving
Efficiently solving problems related to internal space requires both practice and the right approach. By following certain strategies, you can quickly identify the necessary formulas, avoid unnecessary calculations, and ensure accuracy. Speed doesn’t mean sacrificing quality, and with the right techniques, you can streamline the process and arrive at solutions faster.
One key strategy is to first recognize the shape involved in the problem and immediately apply the most relevant formula. Familiarity with common geometric shapes and their corresponding equations allows you to bypass lengthy steps and focus directly on computation. For example, when dealing with a rectangular prism, knowing that the formula is simply length × width × height saves time compared to rethinking the process each time.
Additionally, breaking down the problem into smaller, manageable steps can make a complex question feel less overwhelming. Often, it’s easy to get lost in a multi-step problem, but focusing on one part at a time–like calculating area before moving to the next phase–can lead to faster and more accurate results.
Tip 1: Master Basic Formulas
Having basic formulas memorized is one of the best ways to solve these types of problems quickly. The more familiar you are with common equations for various shapes, the less time you’ll need to spend looking them up or deriving them each time. Practice until the formulas become second nature.
Tip 2: Use Logical Estimation

Sometimes, solving the problem by estimation is a useful shortcut. When exact precision is not necessary, estimating the result before performing detailed calculations can save time. It allows you to quickly gauge whether your final answer is in the correct ballpark.
By mastering these strategies, you’ll be able to approach capacity-related problems with more confidence and speed, improving both your accuracy and efficiency.
Volume Word Problems and Their Solutions
Word problems that require calculating space or capacity often appear more complex than they actually are. The key to solving these challenges is breaking down the problem into smaller, manageable steps and identifying the relevant formula or method to apply. These types of problems often involve real-world scenarios, which helps make abstract concepts more tangible. By practicing these problems, you can improve both your problem-solving skills and your ability to think critically about spatial relationships.
For example, when given a problem about determining the amount of liquid in a container, the first step is to recognize the shape of the container (e.g., rectangular, cylindrical, or irregular) and then apply the appropriate formula. The units involved must also be understood, as they help ensure accuracy in the final result.
Example 1: Calculating Capacity of a Rectangular Tank
Let’s consider a scenario where you’re asked to determine how much liquid a rectangular tank can hold. If the dimensions are provided, such as the length, width, and height, the process is straightforward. Here’s how to solve it:
| Dimension | Value |
|---|---|
| Length | 5 meters |
| Width | 3 meters |
| Height | 2 meters |
| Formula | Length × Width × Height |
| Solution | 5 × 3 × 2 = 30 cubic meters |
This example demonstrates how to approach a word problem by following a clear, logical path from identifying the shape to applying the correct formula. The capacity of the tank, in this case, is 30 cubic meters.
Example 2: Determining the Volume of a Cylindrical Container

For a cylindrical container, the formula involves both the radius of the base and the height of the container. The process is very similar, but the formula differs. Here’s how to solve it:
| Dimension | Value |
|---|---|
| Radius | 2 meters |
| Height | 4 meters |
| Formula | π × Radius² × Height |
| Solution | 3.14 × 2² × 4 = 50.24 cubic meters |
In this case, the volume of the cylindrical container is approximately 50.24 cubic meters. By following a step-by-step method and using the right formula, solving word problems involving space becomes a manageable task.
Reviewing Geometry and Volume Concepts
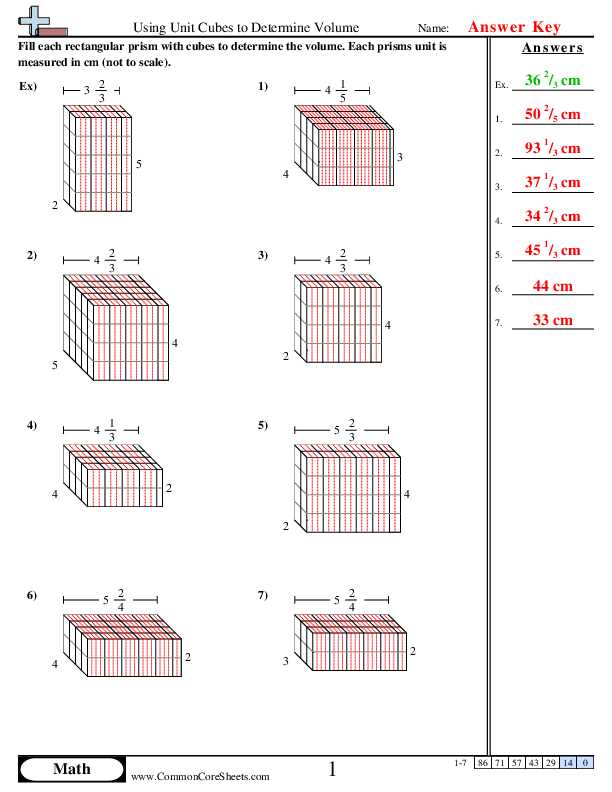
Understanding the principles of space and the relationship between shapes is crucial in solving problems related to dimensions and capacity. To successfully tackle these challenges, it’s important to revisit the foundational concepts of geometry, which include the measurement of lengths, areas, and three-dimensional objects. Once the geometric understanding is solidified, applying it to practical problems involving space becomes much easier.
This section revisits some essential geometric principles, focusing on the key formulas that allow us to calculate space occupied by different objects. A solid grasp of these ideas ensures accuracy in solving real-world problems, whether you’re determining the amount of liquid in a tank or figuring out how much material is needed to fill a container.
Key Geometric Shapes and Their Properties

When it comes to calculating space, it’s essential to understand the properties of different shapes and how they can be used to determine their capacity. Here’s a brief overview of some of the key shapes you will encounter:
| Shape | Key Formula | Notes |
|---|---|---|
| Rectangular Prism | Length × Width × Height | Used for boxes or tanks |
| Cylinder | π × Radius² × Height | Common in pipes, cans, and tanks |
| Sphere | (4/3) × π × Radius³ | Common in balls and tanks |
| Cone | (1/3) × π × Radius² × Height | Used for cones and funnels |
Each shape has its own unique formula, which must be applied correctly to solve problems. Recognizing the shape in a given problem allows you to choose the right approach and achieve accurate results.
Applying Geometry to Real-Life Problems
After understanding the basic properties and formulas of different shapes, the next step is applying this knowledge to practical scenarios. For instance, when tasked with determining how much water a cylindrical tank can hold, you would use the formula for a cylinder, taking into account its radius and height. This is a common example of how geometric principles can be used in everyday problem-solving.
Common Volume Problems in Exams
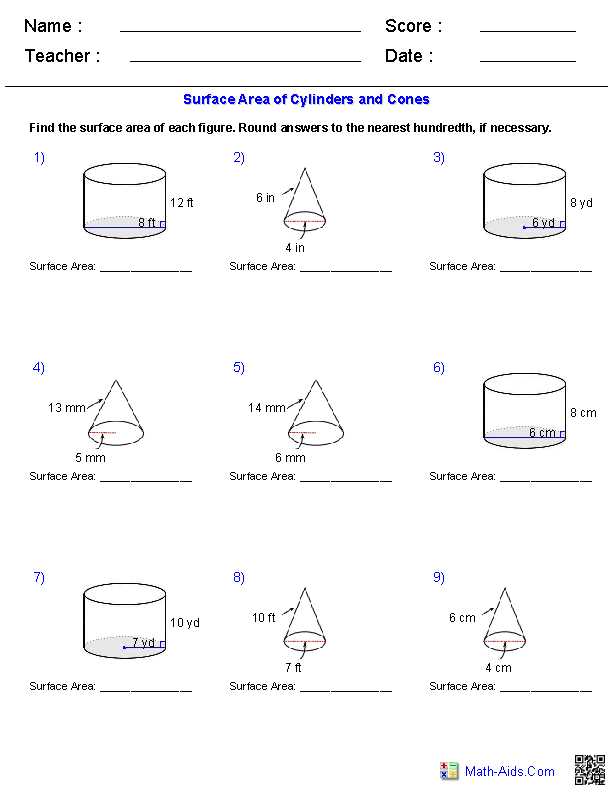
In many academic settings, problems involving the calculation of space or capacity appear regularly in exams. These problems often test your ability to apply mathematical principles to real-life scenarios, requiring you to choose the correct formula and make precise calculations. Understanding how to approach these questions is crucial for performing well in tests and assessments.
This section will highlight some of the most common types of problems you might encounter, along with helpful strategies for solving them. Recognizing these patterns will allow you to efficiently tackle similar problems during exams.
Types of Problems
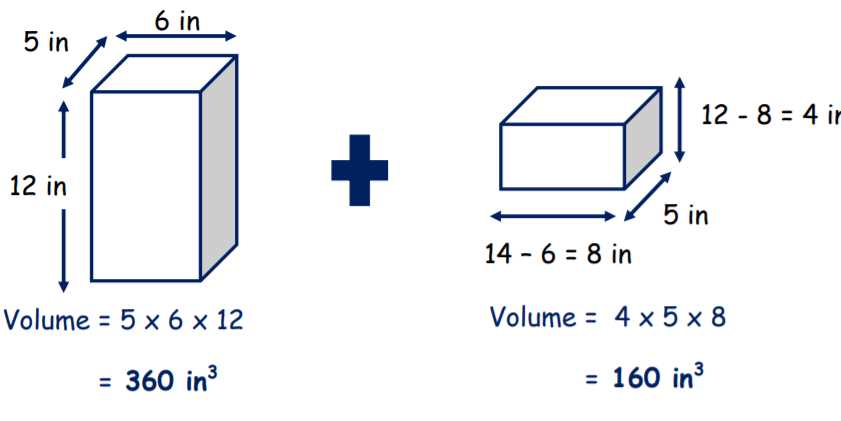
The following are typical examples of problems related to measuring the space within three-dimensional shapes. These problems can appear in various formats, from simple questions to more complex word problems:
- Rectangular Containers – These problems usually involve finding the amount of space inside a box-like object, often requiring you to calculate the product of its length, width, and height.
- Cylindrical Objects – Problems involving cylinders, such as pipes or tanks, often ask for the capacity, which can be calculated using the formula for the area of a circle multiplied by the height.
- Conical Shapes – You may be asked to find the capacity of a cone, which involves a formula that incorporates the area of the base and the height, with a factor of one-third.
- Spherical Measurements – These problems often focus on finding the amount of space inside a sphere, where the formula requires the radius cubed and a constant of pi.
Problem-Solving Strategies
When facing these types of problems in an exam, the following strategies will help you efficiently arrive at the correct answer:
- Identify the Shape: Quickly recognize the geometric shape in question so you can select the right formula.
- List Given Data: Write down all known values, such as dimensions or measurements, and check that they are in the correct units.
- Choose the Right Formula: Apply the appropriate formula based on the shape. Make sure to use the correct version of the formula depending on the context of the problem.
- Perform Calculations: Carefully perform the necessary mathematical operations, paying attention to units and ensuring accuracy.
- Check Your Work: Once you’ve found a solution, double-check your calculations and ensure that your result makes sense in the context of the problem.
By mastering these common problem types and applying these strategies, you’ll be better prepared to tackle similar challenges during exams. Practicing these problems ahead of time will build confidence and help you manage your time more effectively during test situations.
Improving Accuracy in Volume Calculations
Accurate measurement of space within three-dimensional objects is critical in many practical applications, from construction to science experiments. Small errors in calculation can lead to significant discrepancies, affecting the final result. This section explores methods to enhance precision and reduce common mistakes in mathematical calculations of capacity and space.
By focusing on the right techniques and developing good habits, you can increase the likelihood of getting the correct results. Whether you are solving problems involving containers, shapes, or more complex structures, ensuring your calculations are accurate is essential for success.
Key Tips for Accuracy
The following strategies will help you achieve greater accuracy in your calculations:
- Double-check Measurements: Always verify the dimensions provided in a problem. Small errors in reading or recording measurements can lead to significant mistakes in calculations.
- Use Correct Units: Ensure that all your measurements are in the same units before applying formulas. Converting units when necessary can prevent errors in the final result.
- Break Complex Problems into Steps: For complicated problems, break down the calculation into smaller, manageable parts. This reduces the chances of making an error in a single large calculation.
- Apply the Formula Carefully: Choose the appropriate formula for the shape in question and apply it systematically. Mistakes often occur when formulas are applied incorrectly or when values are placed in the wrong parts of the equation.
Techniques for Verification

Once you’ve completed a calculation, it’s important to check your work to ensure its accuracy. Here are a few techniques for verifying your results:
- Estimate Before Solving: Before performing any calculations, try to estimate the final result. This gives you a rough idea of what to expect and helps catch outliers.
- Use a Calculator for Precision: Using a calculator can help reduce human error, especially for complex calculations involving decimals or large numbers.
- Revisit the Problem Statement: Review the problem to make sure you’ve understood it correctly. Sometimes the error lies in misinterpreting the given information.
By applying these strategies and refining your problem-solving approach, you can consistently achieve more accurate results in your calculations. Practice and attention to detail are key to mastering these skills and ensuring precision in all your mathematical tasks.