
Success in advanced mathematics requires a combination of skill, strategy, and consistent practice. Whether you’re aiming to excel or simply improve your understanding, mastering core concepts is essential. Effective preparation involves more than just memorizing formulas–it requires a deep grasp of problem-solving techniques and time management during high-pressure situations.
In this guide, we’ll explore how to navigate complex questions, identify common pitfalls, and implement proven study habits. By focusing on key areas and refining your approach, you can approach each problem with confidence. With a clear plan and dedicated effort, achieving a strong performance on this critical assessment becomes entirely within reach.
Be Ready to Tackle Your AP Test
Achieving top results on a rigorous assessment of advanced mathematics requires both knowledge and strategy. Success depends on understanding core principles, applying them efficiently, and managing time effectively under pressure. A well-rounded approach, with a focus on both theory and practical application, is essential for handling challenging questions with confidence.
Focus on Key Areas
While every topic has its importance, certain areas will appear more frequently in testing scenarios. Concentrating your efforts on mastering these concepts can increase your chances of success. Key areas include:
- Limits and continuity
- Derivatives and their applications
- Integrals and their properties
- Series and sequences
- Graphical interpretations and calculations
Master Problem-Solving Techniques
To succeed in a timed setting, it’s crucial to develop efficient problem-solving techniques. By practicing regularly, you can improve both speed and accuracy. Focus on these strategies:
- Break down complex problems into smaller, manageable steps
- Identify and apply relevant formulas quickly
- Ensure you understand each problem’s context before attempting a solution
- Work through practice tests to familiarize yourself with question patterns
Understand the AP Calculus Exam Format
Familiarity with how an assessment is structured is a key part of effective preparation. Knowing the types of questions, how much time is allotted, and what skills are being tested can help you approach the challenge with confidence. The format is designed to test a wide range of abilities, from problem-solving to conceptual understanding, in both multiple-choice and free-response sections.
The assessment is divided into two major parts, each with a distinct focus. By understanding the specifics of each section, you can better allocate your study time and optimize your performance on test day.
Key Topics to Focus On
Mastering certain core concepts is essential to performing well in any rigorous assessment of advanced mathematics. While there is a broad range of material, focusing on the most critical topics ensures a strong foundation. These areas are not only fundamental but are frequently tested, so dedicating extra time to them can make a significant impact on your overall score.
Pay close attention to:
- Limits and Continuity – Understanding how functions behave near specific points is crucial for many problems.
- Derivatives – Being able to differentiate and interpret the rate of change is key for solving a wide range of questions.
- Integrals – Grasping how to calculate areas and understand the relationship between functions is a core skill.
- Applications of Derivatives – Mastering optimization, related rates, and motion problems is essential for tackling real-world scenarios.
- Fundamental Theorem of Calculus – Connecting differentiation and integration is critical for solving more complex questions.
- Sequences and Series – Understanding convergence, divergence, and approximations will help with more advanced topics.
How to Study Effectively for Calculus
Achieving mastery in advanced mathematics requires a structured and disciplined approach. To excel, it’s essential to break down complex concepts into manageable parts, engage with material regularly, and focus on areas that will have the greatest impact. A solid study plan involves not only reviewing content but also practicing problem-solving under timed conditions to simulate real test scenarios.
Create a Study Schedule

Consistency is key when preparing for any difficult assessment. Set aside specific times each week to focus solely on reviewing mathematical concepts and solving problems. Prioritize areas that challenge you most, but also allocate time to reinforce your strengths. By following a structured schedule, you’ll avoid last-minute cramming and ensure balanced preparation.
Utilize a Variety of Resources
To deepen your understanding, use a combination of textbooks, online tutorials, practice problems, and study groups. Each resource offers unique benefits–textbooks provide in-depth explanations, while practice problems help solidify concepts. Online platforms and videos offer visual aids and alternative explanations that may make complex topics easier to grasp. Working with others can also help clarify difficult material through discussion and shared problem-solving strategies.
Important Tips for Time Management
Efficient time management plays a critical role in ensuring success in any challenging test. It’s not only about managing the clock but also about pacing yourself, prioritizing tasks, and making strategic decisions during the assessment. By mastering time management techniques, you can tackle each section with confidence and leave ample time for review.
Prioritize Key Sections
Start by identifying the areas where you’re most confident and those that require more effort. Spend more time on sections that challenge you, but don’t neglect the ones you find easier. To optimize time during your assessment, consider the following tips:
- Complete familiar questions first to gain momentum and boost your confidence.
- Allocate more time to sections with multiple-step problems or higher point value.
- If you get stuck on a problem, move on and come back to it later to avoid wasting time.
Practice Timed Simulations
One of the most effective ways to improve your timing is through practice. By simulating test conditions at home, you can develop a better sense of how long to spend on each type of problem. Implement these strategies:
- Set a timer for each section during practice sessions to replicate test conditions.
- Track your progress over time to identify areas where you’re consistently spending too much time.
- Review your timed practice tests to assess whether your pacing is improving.
Practice Problems for AP Calculus Success

Consistent practice with a variety of problems is one of the most effective ways to sharpen your problem-solving skills and deepen your understanding of key concepts. Regularly engaging with different types of questions helps you identify common patterns, understand how concepts are applied in various scenarios, and improve your ability to think critically under time pressure. By incorporating practice into your study routine, you can build both confidence and accuracy.
Focus on tackling a range of question types, including those that require multiple steps, abstract reasoning, and graphical interpretations. The more you practice, the better you’ll be able to recognize problem structures and apply the most appropriate methods quickly and effectively.
- Work through past assessments to familiarize yourself with question formats and difficulty levels.
- Try problems that challenge your understanding of both fundamental and advanced topics.
- Focus on questions that require both algebraic manipulation and conceptual reasoning.
Common Mistakes to Avoid During the Exam

Even the most well-prepared individuals can make simple mistakes under pressure. Often, these errors arise from misunderstandings, overlooked details, or time management issues. Being aware of these common pitfalls and actively working to avoid them can make a significant difference in your performance. By focusing on precision and strategy, you can prevent small mistakes from affecting your score.
Here are some of the most frequent errors students make during assessments:
| Common Mistake | How to Avoid It |
|---|---|
| Misreading Questions | Take time to carefully read each problem and underline key terms to ensure you understand what’s being asked. |
| Rushing Through Calculations | Don’t rush. Double-check your work and verify calculations before moving to the next problem. |
| Skipping Units or Labels | Always include necessary units in your final answers and ensure labels are correct when interpreting graphs. |
| Overlooking Graphical Details | Review any graphs carefully to spot subtle details that could influence the solution, like slopes or intercepts. |
| Not Managing Time Properly | Allocate enough time for each section, leaving a few minutes to review your answers at the end. |
Understanding AP Calculus Grading Criteria
Grading in any rigorous assessment is based on specific criteria designed to evaluate your understanding, application, and reasoning skills. Knowing how your performance is assessed can help you focus on the most critical aspects of the test and maximize your score. Understanding the grading system allows you to allocate your efforts effectively and prioritize the areas that matter most to your final result.
Multiple-Choice Section Grading

The multiple-choice section is designed to assess your ability to apply concepts quickly and accurately. Each correct answer adds to your score, but incorrect answers do not penalize you. With this in mind, it’s important to attempt every question, even if you are uncertain about your response.
Free-Response Section Grading

For free-response questions, grading is more complex and involves multiple factors, including:
- Correctness: Each step of your solution is evaluated, and partial credit may be awarded for correctly applying concepts even if the final answer is incorrect.
- Justification: Explanations of your reasoning are crucial. Make sure to show your work and provide clear, logical explanations for each step of your solution.
- Clarity: Organizing your solution clearly helps graders follow your thought process and improves your chances of earning full credit.
Best Resources for AP Calculus Review
To succeed in any challenging subject, it’s essential to use a variety of resources that cater to different learning styles. Leveraging multiple materials, including textbooks, websites, and practice tools, can deepen your understanding and help you approach problems from different perspectives. Whether you prefer visual explanations, interactive exercises, or detailed theory, the right resources can enhance your preparation.
Here are some of the most effective tools to incorporate into your study routine:
| Resource | Why It’s Useful |
|---|---|
| College Board Website | Provides official practice tests, scoring guidelines, and course descriptions that align with the real assessment format. |
| Khan Academy | Offers free instructional videos and practice problems on key topics, perfect for visual learners and those who need clear explanations. |
| AP Calculus Review Books | These comprehensive guides include practice questions, test-taking strategies, and detailed explanations for solving various problems. |
| AP Classroom | Interactive online platform providing practice questions, quizzes, and feedback tailored to your individual progress. |
| PatrickJMT | Great for quick, concise math tutorials and walkthroughs of specific types of problems, especially for on-the-go review. |
How to Handle Stress on Exam Day
Managing anxiety and staying calm during a high-pressure situation is crucial for performing at your best. Stress can cloud your judgment and make even the simplest tasks seem overwhelming. The key to managing this is preparation and employing strategies to maintain focus and calmness throughout the assessment.
Effective Techniques for Managing Anxiety
When stress starts to build, using proven techniques can help you stay in control. These strategies help you center your thoughts, regulate your breathing, and stay mentally focused.
- Practice Relaxation Techniques: Deep breathing exercises or progressive muscle relaxation can help calm your nerves.
- Positive Visualization: Visualize yourself solving problems confidently and achieving success, which can help alleviate fear and improve focus.
- Stay Organized: Plan your time carefully and don’t rush through questions. Staying organized helps reduce feelings of overwhelm.
Maintaining a Balanced Mindset
Keeping a positive mindset is crucial when facing a challenging situation. Rather than focusing on the pressure, focus on your strengths and progress.
| Tip | How It Helps |
|---|---|
| Take Breaks | Short, scheduled breaks can prevent burnout and help you maintain focus throughout the duration of the test. |
| Stay Hydrated | Drinking water helps keep your body and mind functioning at their best, reducing stress and boosting energy levels. |
| Keep Perspective | Remember, one test does not define your abilities. Maintain a balanced view and focus on doing your best. |
Using Graphing Calculators Efficiently

Mastering the use of a graphing calculator can greatly enhance your ability to solve complex problems quickly and accurately. While these devices are powerful tools, knowing when and how to use them effectively is key. Over-relying on the calculator can limit your understanding of core concepts, but using it strategically can save time and help verify your solutions.
Key Features to Utilize
Graphing calculators come with a variety of functions that can simplify problem-solving. Familiarize yourself with these features to make the most of your device.
- Graphing Functions: Use the graphing feature to visualize equations and analyze trends. This helps in understanding behavior, limits, and intersections.
- Derivative and Integral Calculations: Take advantage of built-in derivative and integral functions to check your manual calculations and save time.
- Solving Equations: Use the solver tool to find zeros, intersections, or roots of equations, which is especially helpful when dealing with complicated functions.
Best Practices for Effective Use
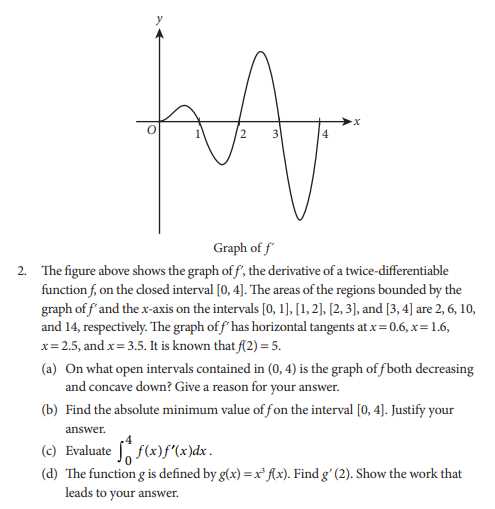
To ensure you’re using your graphing calculator efficiently, it’s important to integrate it into your study routine and know its limitations.
- Practice with it Regularly: Familiarize yourself with all the features well in advance of any assessment. This ensures you’re comfortable using the device under time pressure.
- Don’t Overuse It: Avoid using the calculator for every problem. Relying too heavily on it can reduce your ability to solve problems manually, which is often required for full understanding.
- Check Your Work: After solving problems by hand, use the graphing calculator to verify your results. This helps catch any mistakes and reinforces your understanding.
Strategies for Answering Multiple-Choice Questions
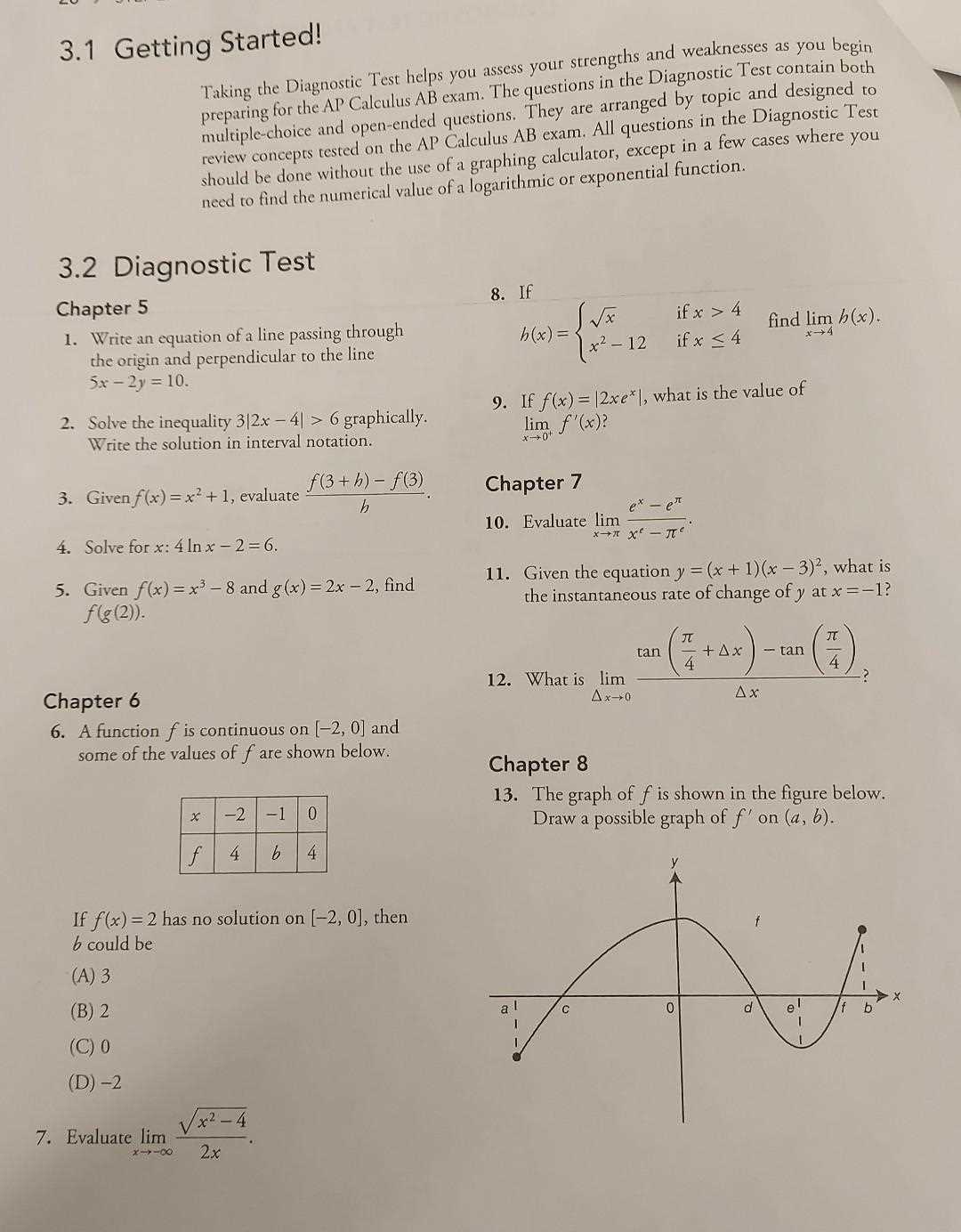
When tackling multiple-choice questions, employing effective strategies can make a significant difference in how you approach and solve each problem. These questions often require quick decision-making and a solid understanding of key concepts. Knowing how to evaluate each option and using elimination techniques can increase your chances of selecting the correct answer.
Key Techniques for Success
Approaching multiple-choice questions with a structured method will help you maximize your efficiency and accuracy. Here are some essential strategies to implement:
- Read Carefully: Pay close attention to every word in the question and all available options. Small details can drastically change the meaning of the question and the answer.
- Eliminate Clearly Incorrect Choices: Start by ruling out obviously wrong options. This increases your odds of selecting the correct answer if you need to guess.
- Consider All Options: Even if one answer seems right, double-check the other options to avoid overlooking a better answer.
- Look for Clues in the Question: Sometimes, hints or patterns within the question itself can guide you toward the right solution. Pay attention to wording, units, or familiar formulas that might be referenced.
Time Management Tips
Time is often a critical factor in answering multiple-choice questions effectively. Managing your time efficiently ensures you have enough time to address every question thoughtfully.
- Move Quickly, But Thoughtfully: Don’t spend too much time on a single question. If you’re unsure, make your best guess and move on to the next one.
- Return to Tough Questions: If you have time left at the end, revisit difficult questions. This way, you won’t risk spending too much time on any one question at the start.
Mastering Free-Response Question Techniques
Free-response questions provide an opportunity to demonstrate your problem-solving skills in a structured and detailed manner. Unlike multiple-choice questions, these require a deeper understanding of concepts and the ability to clearly communicate your work. Approaching these questions with the right techniques can help you maximize your score and ensure that you address all aspects of the problem.
Step-by-Step Approach to Solving Problems
To effectively tackle free-response questions, it’s important to break down each problem into manageable steps. This method not only keeps you organized but also ensures that you don’t overlook any critical components.
- Read the Problem Carefully: Understand what is being asked before jumping into calculations. Pay attention to keywords like “find”, “evaluate”, and “explain” to know exactly what is required.
- Organize Your Work: Write down all known information and formulas before starting calculations. This can help you stay on track and ensure your answer is clearly explained.
- Show All Steps: Provide detailed reasoning and intermediate steps. Partial credit can often be earned for showing your thought process, even if the final answer is incorrect.
Common Pitfalls and How to Avoid Them
While free-response questions offer more freedom, they also come with unique challenges. Being aware of common mistakes can help you avoid them during the test.
| Common Mistakes | How to Avoid Them |
|---|---|
| Skipping steps | Always show your work, even if it seems unnecessary. This will ensure clarity and help you avoid losing points for incomplete reasoning. |
| Failure to explain reasoning | Don’t just write the final answer. Explain how you arrived at the solution to demonstrate your understanding. |
| Rushing through calculations | Take your time and double-check your calculations to ensure accuracy. A small mistake can cost valuable points. |
Key Formulas You Must Memorize
In any high-level math test, knowing essential equations and relationships is crucial. These formulas serve as building blocks for solving complex problems and can significantly streamline your approach. Familiarity with the key expressions allows you to save time and approach each problem with confidence.
Below are some of the most important formulas that will help you excel in your preparation. Memorizing these will ensure you’re ready to tackle a wide variety of questions with efficiency.
Fundamental Differentiation and Integration Rules
These basic rules are the foundation for solving a range of problems, from rates of change to area calculations.
- Power Rule: d/dx (x^n) = n * x^(n-1)
- Product Rule: d/dx [u(x) * v(x)] = u'(x) * v(x) + u(x) * v'(x)
- Quotient Rule: d/dx [u(x) / v(x)] = (v(x) * u'(x) – u(x) * v'(x)) / v(x)^2
- Chain Rule: d/dx [f(g(x))] = f'(g(x)) * g'(x)
- Integration of x^n: ∫ x^n dx = (x^(n+1)) / (n+1) + C (for n ≠ -1)
Important Theorems and Properties
These principles are vital for understanding deeper concepts such as limits, continuity, and approximation techniques.
- Fundamental Theorem of Calculus: ∫_a^b f(x) dx = F(b) – F(a), where F'(x) = f(x)
- Mean Value Theorem: f'(c) = (f(b) – f(a)) / (b – a), where c is in (a, b)
- L’Hopital’s Rule: lim (x→a) [f(x) / g(x)] = lim (x→a) [f'(x) / g'(x)], if the limit yields an indeterminate form like 0/0 or ∞/∞
Critical Trigonometric Identities
Trigonometric functions appear frequently in problems involving oscillations, motion, and rates of change. Here are the identities you need to recall:
- Sine and Cosine Addition Formulas: sin(A ± B) = sin(A)cos(B) ± cos(A)sin(B), cos(A ± B) = cos(A)cos(B) ∓ sin(A)sin(B)
- Double Angle Formulas: sin(2x) = 2sin(x)cos(x), cos(2x) = cos²(x) – sin²(x)
- Pythagorean Identity: sin²(x) + cos²(x) = 1
Having these formulas memorized will allow you to tackle a range of problems effectively, saving you time and minimizing errors. Regular practice with these key equations ensures that you will be ready to handle the most challenging problems with confidence.
Understanding Limits and Derivatives
Grasping the concepts of limits and derivatives is crucial to solving a wide range of mathematical problems. These two concepts are interrelated and serve as the backbone of many more advanced ideas in analysis. Limits provide a foundation for understanding how functions behave near certain points, while derivatives describe the rate of change of functions at those points. Together, they form a powerful toolset for analyzing dynamic systems.
Limits: The Foundation of Change
Limits describe the behavior of a function as it approaches a specific value. Understanding how functions behave near a given point is essential when solving problems that involve continuity, asymptotes, or indeterminate forms.
- Formal Definition: lim (x→a) f(x) = L means that as x gets closer to a, the value of f(x) approaches L.
- One-Sided Limits: lim (x→a⁺) f(x) represents the value of f(x) as x approaches a from the right, and lim (x→a⁻) f(x) represents the value from the left.
- Indeterminate Forms: Limits can sometimes result in forms like 0/0 or ∞/∞. In these cases, techniques such as L’Hopital’s Rule or algebraic manipulation are used to resolve them.
Derivatives: Describing Rates of Change
Derivatives measure how a function changes as its input changes. They tell us about the slope of a curve at any given point and are used to determine velocity, acceleration, and many other rates of change in real-world applications.
- Definition: The derivative of a function at a point is the limit of the average rate of change as the interval approaches zero: f'(x) = lim (h→0) [f(x+h) – f(x)] / h.
- Geometric Interpretation: The derivative represents the slope of the tangent line to the curve at a specific point. A positive derivative means the function is increasing, while a negative derivative means the function is decreasing.
- Higher-Order Derivatives: Derivatives can be taken repeatedly. The second derivative, f”(x), represents the rate of change of the rate of change and is useful for analyzing concavity and acceleration.
Mastering limits and derivatives is essential not only for solving abstract mathematical problems but also for understanding real-world phenomena where change is constant. Regular practice with these concepts will build a solid foundation that you can rely on when tackling more complex scenarios.
How to Approach AP Calculus Word Problems
Solving word problems in mathematics requires not only understanding of the core concepts but also the ability to translate real-world scenarios into mathematical language. These problems often involve multiple steps, and the key to solving them efficiently is a systematic approach. Breaking down the problem into smaller parts and applying appropriate methods will lead to a structured solution. Below are steps to approach these types of questions effectively.
Step-by-Step Approach
By following a logical sequence, you can avoid confusion and reduce the chance of making errors in interpretation or calculation.
- Read the Problem Carefully: Start by reading through the problem statement multiple times to ensure you fully understand what is being asked. Highlight or underline key information such as known values, variables, and the objective of the problem.
- Identify Variables: Define any unknowns with variables. This will help you to form equations and set up your solution method. Label all quantities clearly and ensure you understand their units and relationships.
- Translate to Mathematical Terms: Convert the word problem into a mathematical expression or equation. Look for relationships between quantities, such as rates of change or areas, and express these in terms of functions or derivatives.
- Choose the Right Method: Once the problem is translated, choose the most appropriate technique. It could involve finding derivatives, integrating, applying limits, or solving algebraic equations. Think about what tools from previous lessons could help solve the problem.
- Perform Calculations: Solve the equation or inequality step by step. Be sure to keep track of units and verify intermediate results to avoid errors. If the problem involves optimization or related rates, set up your equations carefully and solve them in sequence.
- Check Your Work: Once you reach a solution, check it against the context of the problem. Does the answer make sense? Have you used the correct values and methods? Ensuring accuracy is critical to getting the right result.
Common Problem Types
Word problems often fall into specific categories. Familiarity with these will allow you to anticipate the method you’ll need to use and speed up your solving process.
- Optimization Problems: These require finding maximum or minimum values for a given function. Identify constraints, define variables, and take derivatives to find critical points.
- Related Rates Problems: These involve situations where two or more quantities change with respect to time. Set up a relationship between the variables, differentiate implicitly, and solve for the rate of change of the desired quantity.
- Area and Volume Problems: These questions often ask for the area under a curve or the volume of a solid. Set up integrals based on the limits provided in the problem.
Approaching word problems with a structured method will help you stay organized and avoid getting overwhelmed by complex situations. The more you practice these strategies, the more confident you’ll become in identifying key elements and applying the right techniques efficiently.
Utilizing Study Groups for AP Calculus
Collaborative learning through study groups can significantly enhance your understanding of complex mathematical concepts. Working with peers allows you to share different approaches to problems, clarify doubts, and reinforce your knowledge. A well-organized study group fosters mutual support and accountability, making it easier to stay on track while preparing for difficult topics.
Benefits of Joining a Study Group

Study groups provide a variety of advantages when it comes to mastering tough material and preparing for assessments. Below are some key benefits:
- Different Perspectives: Each member brings a unique approach to solving problems. This diversity can expose you to new techniques and methods that you may not have considered.
- Clarification of Concepts: Explaining concepts to others reinforces your own understanding. Additionally, you can ask your peers to explain concepts you find confusing, allowing for quicker clarification than studying alone.
- Motivation and Accountability: Regular group meetings help keep everyone motivated and on task. The commitment to meet regularly encourages consistency in your study schedule.
- Peer Support: Study groups offer emotional support during stressful periods. Working with others helps reduce anxiety and makes the preparation process feel less overwhelming.
Effective Study Group Strategies

Maximize the value of your study sessions by following these strategies to make the most of your group time:
- Set Clear Goals: At the start of each session, decide on specific topics or problems to tackle. This ensures that your group remains focused and makes efficient use of time.
- Divide Responsibilities: Assign each person specific topics or chapters to review before meetings. This way, everyone can contribute their expertise to the group, ensuring a broader coverage of material.
- Practice Active Participation: Engage actively in discussions, whether it’s asking questions, providing solutions, or helping others understand tricky concepts. This active involvement solidifies your own learning.
- Review Together: After working through problems, take time to review solutions as a group. This allows everyone to identify any mistakes and learn from them collectively.
- Keep it Consistent: Schedule regular sessions to keep everyone on track. Consistency is key to reinforcing what you’ve learned and addressing new challenges as they arise.
By combining individual study efforts with collaborative group work, you can build a deeper understanding of key topics and feel more confident heading into assessments. Make sure your group is focused, collaborative, and committed to helping each other succeed.
Reviewing Past AP Calculus Exams
Analyzing previous assessment papers is a crucial step in honing your skills and gaining insight into recurring question patterns. By reviewing past materials, you can become familiar with the structure of questions, understand the level of difficulty, and identify frequently tested concepts. This process not only builds confidence but also helps improve time management during the actual test.
Why Reviewing Past Papers is Essential

Past assessments serve as valuable practice tools. They provide a comprehensive overview of the topics covered and give you an opportunity to identify areas where you might need further improvement. By simulating actual conditions, you can test your knowledge under time constraints and refine your problem-solving abilities. Below are some specific benefits:
- Familiarity with Question Types: By working through past papers, you gain exposure to various question formats, helping you recognize common patterns and preparing you to tackle any challenges more efficiently.
- Improved Time Management: Repeatedly practicing under timed conditions enhances your ability to allocate time wisely across sections, ensuring that you can answer every question within the allotted time frame.
- Confidence Building: Regularly completing previous assessments reinforces your knowledge and gives you a realistic sense of what to expect, reducing anxiety and boosting self-assurance.
How to Effectively Review Past Papers
To get the most out of reviewing previous tests, it’s important to approach the practice with focus and strategy. Consider the following tips to optimize your review sessions:
- Start Early: Begin your review well in advance of your scheduled preparation period. Spreading out the work allows you to identify weaknesses and address them methodically.
- Work in Simulated Conditions: Recreate the test environment by adhering to time limits and avoiding distractions. This practice can help you learn how to stay calm and focused on the task at hand.
- Review Mistakes Thoroughly: After completing each paper, take the time to go over your errors in detail. Understanding why you made certain mistakes allows you to prevent them from happening again in the future.
- Focus on Key Concepts: Make note of topics that appear frequently and ensure you’re comfortable solving related problems. Pay extra attention to areas where you struggle and seek clarification if needed.
- Track Your Progress: Keep a record of your performance on each past paper to monitor improvement over time. This allows you to identify areas that still need work, while also celebrating your successes.
By reviewing past assessments, you’ll be better equipped to approach future questions with confidence and clarity. It serves as an effective way to reinforce knowledge, build problem-solving skills, and boost your readiness. Make it a key part of your preparation strategy to ensure you’re fully prepared for whatever challenges lie ahead.