
In any learning process, understanding core principles and techniques is essential for success. As students move through more complex topics, they often encounter challenges that require both practice and a solid grasp of foundational concepts. This section is designed to help learners navigate these difficulties by providing detailed explanations and solutions to common problem types encountered in advanced courses.
By breaking down each challenge into manageable steps, students can gain confidence in their problem-solving abilities. Through consistent practice and careful analysis, they can develop the skills necessary to tackle even the most intricate exercises. This approach not only aids in mastering the material but also fosters a deeper appreciation for the logical structure behind each problem.
Effective learning is not just about memorizing formulas or steps; it involves understanding the reasoning behind each solution. With clear, step-by-step guidance, students can improve their ability to approach difficult tasks methodically and accurately. Whether preparing for exams or working through assignments, these strategies will help ensure success in any advanced study.
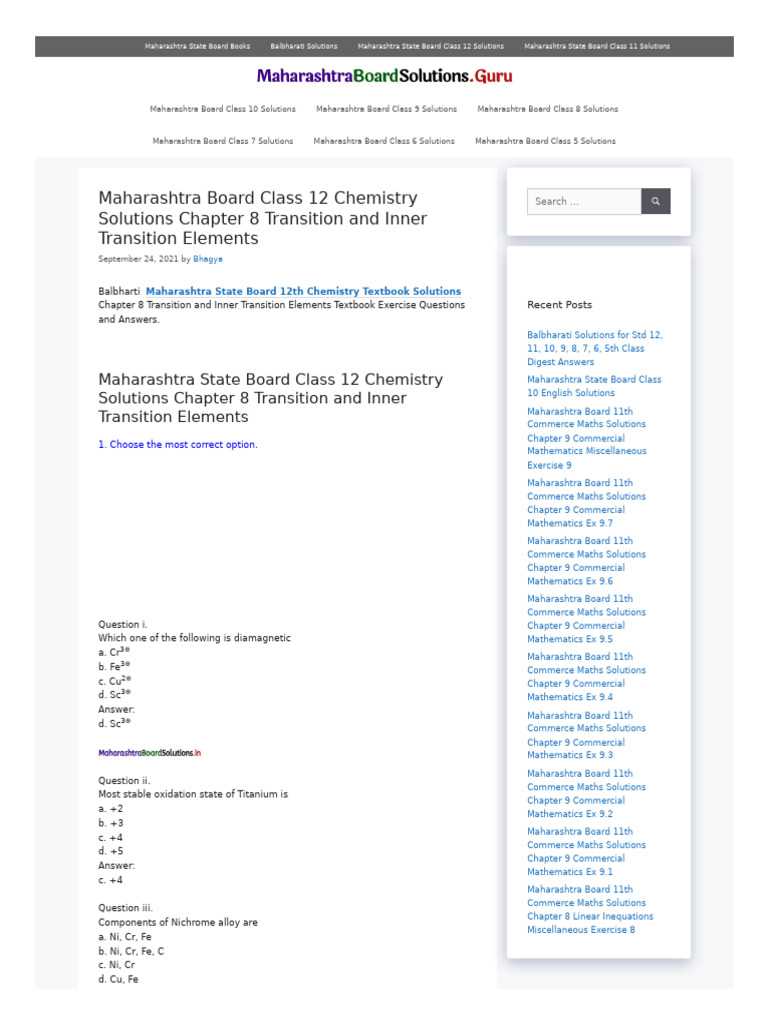
Transition Mathematics Textbook Answers
Understanding the process of solving complex problems requires more than just applying formulas. It is about developing the ability to break down each task, identify key steps, and find logical solutions. In this section, we will explore various approaches to handling exercises that challenge students and provide effective methods for addressing these tasks. The focus is on providing a clearer path to solve problems by demonstrating how to methodically work through each stage of the process.
Effective Problem-Solving Strategies
One of the most crucial aspects of mastering advanced topics is recognizing patterns in problems. Each exercise typically follows a structure that, once identified, can make solving it much more straightforward. Through practice, students can learn how to predict the necessary steps and apply the appropriate techniques to find the correct solutions efficiently.
Common Mistakes and How to Avoid Them
Many learners encounter similar errors while attempting to solve challenging problems. These mistakes can range from misinterpreting the question to overlooking essential steps in the solution process. By understanding these common pitfalls, students can better prepare themselves to avoid these issues and improve their overall problem-solving ability.
| Problem Type | Common Mistakes | Solution Tips |
|---|---|---|
| Linear Equations | Skipping steps when isolating variables | Always check each step and verify results |
| Word Problems | Misunderstanding the context or conditions | Carefully read and break down the problem statement |
| Quadratic Equations | Incorrect factorization | Double-check factors and practice more problems |
Understanding the Importance of Transition Math

The ability to work through advanced problem-solving tasks is essential for any student moving from basic to more complex academic challenges. As learners progress, they encounter exercises that require not only a strong grasp of foundational concepts but also the ability to apply those concepts in more intricate ways. The importance of this stage in learning cannot be overstated, as it forms the bridge between simple computations and higher-level analytical thinking.
Building Strong Foundations for Future Learning
At this stage, students refine their understanding of earlier principles while preparing for even more advanced topics. This phase helps to strengthen critical thinking skills, which are essential for tackling unfamiliar problems. Through consistent practice and applying different techniques, students develop confidence in their ability to manage new and challenging material.
Enhancing Problem-Solving Skills
As students progress, they are encouraged to not only find solutions but also to understand the process behind each step. Mastery of techniques becomes crucial, as it enables learners to adapt to various types of questions and scenarios. This stage encourages an in-depth approach, teaching students how to approach each task logically and systematically.
How to Approach Math Problems Effectively
To solve complex problems with ease, it is essential to develop a systematic approach. Rather than jumping straight into calculations, taking the time to understand the problem and organize your thoughts can significantly improve accuracy and efficiency. By breaking down the task into smaller, manageable steps, students can navigate even the most challenging exercises with confidence.
Understand the Problem First
Before attempting to solve any problem, it is crucial to fully comprehend what is being asked. Carefully read through the question, identifying key information and what needs to be found. A clear understanding of the problem’s requirements helps to determine which methods and formulas are appropriate. This first step lays the foundation for a successful solution.
Break Down Complex Steps
When faced with complicated problems, try to simplify them by dividing them into smaller, more straightforward tasks. Each part can be tackled individually, making the entire process more manageable. By addressing one step at a time, students can focus their attention on solving smaller problems, which ultimately lead to the correct solution. This technique is especially helpful in avoiding confusion and ensuring that no crucial step is overlooked.
Patience and practice are key to mastering this method. With time, learners will develop the ability to assess problems quickly and identify the most effective approach for solving them.
Key Concepts in Transition Mathematics

Mastering more advanced topics requires a deep understanding of the fundamental principles that serve as the building blocks for complex problem-solving. These core ideas provide the foundation for tackling new concepts and performing calculations with accuracy. By focusing on key principles and strategies, students can navigate through increasingly difficult exercises with greater ease and confidence.
Algebraic Fundamentals
One of the cornerstones of more advanced problem-solving is a strong command of algebraic techniques. Recognizing patterns, simplifying expressions, and solving equations are essential skills that students need to refine. Developing a thorough understanding of these concepts allows learners to manipulate variables effectively and apply them to a variety of scenarios.
Functions and Their Applications
Functions are central to solving many types of problems, as they describe the relationship between variables. Understanding how to work with different types of functions–whether linear, quadratic, or exponential–is critical. Students must learn how to interpret and analyze these relationships, as well as how to manipulate them in order to find solutions to real-world problems.
Step-by-Step Solutions for Common Problems
One of the most effective ways to master complex problems is to break them down into smaller, more manageable steps. By following a clear and structured approach, students can tackle even the most challenging exercises with greater confidence and accuracy. This section provides detailed solutions to common types of problems, showing how to systematically address each stage of the problem-solving process.
Solving Linear Equations

Linear equations are a fundamental part of problem-solving. To solve these types of problems, the first step is to isolate the variable. Begin by simplifying the equation, combining like terms where necessary, and then perform operations to get the variable on one side. Once the variable is isolated, solving for its value becomes straightforward.
Example: Solve for x in the equation 3x + 5 = 14.
1. Subtract 5 from both sides: 3x = 9
2. Divide both sides by 3: x = 3
This step-by-step approach ensures clarity and helps avoid errors along the way.
Working with Quadratic Equations
Quadratic equations require a slightly more complex approach, often involving factoring, completing the square, or using the quadratic formula. The method you choose will depend on the specific form of the equation, but each approach follows a logical sequence to find the solutions. Begin by ensuring the equation is in standard form (ax² + bx + c = 0), then proceed with the most appropriate method.
Example: Solve x² + 5x + 6 = 0 by factoring.
1. Factor the quadratic expression: (x + 2)(x + 3) = 0
2. Set each factor equal to zero: x + 2 = 0 or x + 3 = 0
3. Solve for x: x = -2 or x = -3
This clear breakdown helps students understand how to approach similar problems with ease.
Understanding the Role of Variables
In problem-solving, variables play a crucial role by representing unknown values that we seek to find. These symbols allow us to express relationships and equations in a general form, making it easier to manipulate and solve for specific values. A solid understanding of how variables function is key to successfully solving a wide range of problems.
Why Variables Matter
Variables allow us to generalize problems, creating formulas and expressions that can be applied to different scenarios. Instead of working with specific numbers, we use letters or symbols to stand for unknown quantities. This flexibility enables us to explore multiple possibilities and solve problems without needing to know every detail upfront.
Manipulating Variables in Equations
When working with equations, it is essential to understand how to manipulate variables to isolate them and find their values. Whether through addition, subtraction, multiplication, or division, the goal is to perform operations that maintain the equality of both sides of the equation. This process of isolating the variable is a foundational skill in solving problems.
Example: Solve for x in the equation 2x + 3 = 11.
1. Subtract 3 from both sides: 2x = 8
2. Divide both sides by 2: x = 4
Through this process, we see how manipulating the variable leads us to the desired solution.
Why Practice is Crucial in Mathematics
In any subject, repetition is key to mastering the concepts, and this is especially true when it comes to solving complex problems. Consistent practice reinforces learning, helping to solidify understanding and increase speed. The more a student practices, the more familiar they become with different types of problems and solution strategies. This ultimately leads to greater confidence and improved performance.
Benefits of Regular Practice
- Improves Problem-Solving Speed: With regular practice, students become quicker at recognizing patterns and applying solutions.
- Builds Confidence: Successfully solving problems strengthens a learner’s belief in their abilities.
- Enhances Retention: Repetition helps commit key concepts and methods to memory, making it easier to recall them when needed.
- Identifies Weak Areas: Regular practice allows students to pinpoint areas that need improvement and focus on them.
How Practice Translates to Mastery
Effective practice involves more than just completing exercises; it requires thoughtful reflection on mistakes and finding ways to improve. Here are a few strategies to maximize the benefits of practice:
- Work on a Variety of Problems: Tackle problems of different difficulty levels to ensure a well-rounded understanding.
- Focus on Mistakes: Analyze errors to understand why they occurred and how to avoid them in the future.
- Set Achievable Goals: Aim to solve a specific number of problems each day to maintain steady progress.
Through intentional and consistent practice, learners can gradually master even the most challenging concepts, ultimately leading to success in solving complex problems.
Methods for Simplifying Complex Equations

When faced with complex problems, it is essential to break them down into simpler, more manageable components. By using specific techniques to simplify equations, students can make the process of finding solutions more straightforward. These methods help to eliminate unnecessary complexity, making it easier to identify the key elements and solve for the unknowns efficiently.
Factoring Expressions
Factoring is one of the most common methods for simplifying complex equations. It involves rewriting an equation as a product of simpler terms. This approach is particularly useful for quadratic expressions, as it allows students to solve equations by setting each factor equal to zero. Factoring also helps to identify potential common factors that can be reduced or eliminated.
Example: Simplify and solve the equation x² + 5x + 6 = 0 by factoring.
1. Factor the quadratic expression: (x + 2)(x + 3) = 0
2. Set each factor equal to zero: x + 2 = 0 or x + 3 = 0
3. Solve for x: x = -2 or x = -3
Combining Like Terms
Another effective way to simplify equations is by combining like terms. This method involves adding or subtracting terms that have the same variable and exponent. Simplifying these terms reduces the equation to a more manageable form and makes it easier to solve for the unknown.
Example: Simplify the equation 4x + 7x – 3 = 12.
1. Combine like terms: 11x – 3 = 12
2. Add 3 to both sides: 11x = 15
3. Divide both sides by 11: x = 15/11
By applying these techniques, students can reduce the complexity of equations, making them easier to solve and less prone to errors.
Identifying Common Mistakes in Math Answers
When solving complex problems, it’s easy to make simple mistakes that can lead to incorrect results. Recognizing these common errors is an essential skill, as it helps learners avoid repeating the same mistakes and improve their problem-solving accuracy. By understanding the most frequent pitfalls, students can develop a more reliable approach to solving equations and expressions.
Common Errors in Calculation

One of the most common mistakes in problem-solving is performing arithmetic operations incorrectly. This can include errors in addition, subtraction, multiplication, and division. Even a small misstep can lead to significant mistakes in the final solution.
Example: Solve for x in the equation 3x + 7 = 16.
1. Subtract 7 from both sides: 3x = 9
2. Incorrect division: x = 9/3 (Correct: x = 3)
Miscalculations like these often occur when a student rushes through the process or overlooks a step. Taking time to double-check each operation can help reduce errors.
Overlooking Negative Signs
Another frequent mistake is neglecting negative signs when solving equations. Negative signs often get overlooked, leading to incorrect answers that may be off by a factor of negative one.
Example: Solve for x in the equation -4x = 20.
1. Divide both sides by -4: x = -5 (Incorrect: x = 5 is a common mistake)
Overlooking the negative sign often happens when students work too quickly or forget to distribute negative values properly. It’s important to pay close attention to signs throughout the process.
Identifying Errors in the Table of Common Mistakes
| Type of Mistake | Example | Solution |
|---|---|---|
| Arithmetic Error | 3x + 7 = 16, solving x = 3 | Double-check division step: x = 3 |
| Sign Error | -4x = 20, solving x = 5 | Remember to divide by negative value: x = -5 |
| Distributive Error | 2(x + 3) = 14 | Distribute correctly: 2x + 6 = 14, then solve |
By recognizing and understanding these common mistakes, students can better navigate the problem-solving process, leading to more accurate and efficient solutions.
Tools and Resources for Math Learners

In the journey to mastering problem-solving techniques, having the right tools and resources can make all the difference. Whether you are looking to deepen your understanding, get immediate help with problems, or test your skills, the right support can provide the guidance you need to succeed. This section highlights a variety of tools and platforms that can help learners at all levels enhance their skills and boost their confidence.
Online Tools for Practice and Support
There are several online platforms designed to help students practice problems and receive instant feedback. These tools allow learners to work through exercises, learn at their own pace, and gain a better understanding of concepts that may be difficult to grasp. Some of the most popular resources include:
- Khan Academy: Offers free video tutorials, interactive exercises, and personalized learning dashboards.
- Wolfram Alpha: A computational engine that can solve problems and explain steps in real-time.
- Desmos: An online graphing calculator that helps visualize functions and equations.
- Quizlet: Allows users to create custom study sets and practice with flashcards and quizzes.
Offline Resources and Tools

In addition to online resources, there are many offline tools that can help reinforce learning. Textbooks, workbooks, and guides can provide a more structured learning experience, while tools such as calculators and graphing paper remain essential for hands-on practice.
- Calculator: A reliable tool for checking arithmetic and solving more complex equations.
- Graphing Paper: Useful for plotting points, understanding functions, and visualizing problems.
- Practice Workbooks: Offer a collection of problems and solutions that can help reinforce specific skills.
- Study Groups: Working with peers in study groups can provide mutual support and foster deeper understanding.
Utilizing a mix of both online and offline resources helps to create a balanced learning environment, ensuring that students can tackle challenges from different angles. With these tools, learners can stay engaged, motivated, and confident in their ability to solve problems successfully.
Common Techniques for Solving Algebraic Problems
Solving algebraic problems often requires applying specific strategies to simplify complex expressions or equations. Understanding these techniques can significantly improve problem-solving efficiency and accuracy. From basic manipulation of terms to more advanced methods, mastering a variety of approaches ensures flexibility in tackling a wide range of problems. This section explores some of the most common methods used to solve algebraic challenges.
Fundamental Approaches for Basic Equations
For simpler algebraic problems, certain techniques are particularly effective in isolating the unknowns and finding their values. These methods are foundational and widely used in many algebraic contexts:
- Isolation of Variables: Rearranging the equation so that the variable of interest stands alone on one side, allowing for easy calculation.
- Combining Like Terms: Simplifying expressions by adding or subtracting terms with the same variable or constants.
- Cross-Multiplication: Used primarily in rational equations, this technique involves multiplying both sides by the denominators to eliminate fractions.
- Distribution: Applying the distributive property to eliminate parentheses and simplify the expression.
Advanced Methods for Solving Complex Problems
For more complex problems, advanced techniques are necessary to solve equations with multiple variables or higher degrees. These methods are typically introduced after mastering the basics:
- Factoring: Breaking down polynomials into simpler expressions (binomials) to find solutions more easily, particularly useful for quadratic equations.
- Substitution Method: Replacing one variable with an equivalent expression to simplify the system of equations and find solutions for the unknowns.
- Quadratic Formula: A standard formula used to find the solutions of any quadratic equation in the form ax² + bx + c = 0.
- Graphing: Plotting equations on a coordinate plane to visually find the points of intersection or solutions to the equation.
By applying these methods, students and learners can approach algebraic problems more confidently. Whether solving for a single unknown or working with complex systems, these techniques form the backbone of effective problem-solving in algebra.
How to Tackle Word Problems in Math
Word problems can often seem overwhelming due to the amount of information presented in sentence form. However, with a systematic approach, these problems can be broken down into manageable parts. The key to success lies in translating the written scenario into mathematical terms and solving it step by step. This section discusses effective strategies for tackling word problems and converting them into solvable equations.
Step-by-Step Approach to Word Problems

To solve word problems efficiently, it is important to follow a structured process. Here’s a general outline for approaching these problems:
- Read the problem carefully: Pay close attention to the details provided. Underline or highlight key information such as quantities, relationships, and unknowns.
- Identify what is being asked: Clearly determine the question being asked in the problem. Are you solving for a specific variable, a total, or a difference?
- Define the variables: Assign variables to the unknown quantities. This step simplifies the problem by turning words into mathematical symbols.
- Set up an equation: Translate the relationships described in the problem into an algebraic equation. Use the information provided to form a solvable equation.
- Solve the equation: Apply the appropriate mathematical techniques, such as isolating variables or using arithmetic operations, to solve the equation.
- Check your solution: Once you have a solution, go back to the problem and verify if it makes sense in the context of the situation described.
Common Strategies for Complex Word Problems
For more complex word problems, additional strategies may be required to break them down further:
- Look for patterns: In some word problems, identifying a pattern in the information provided can help in forming a more efficient solution.
- Draw a diagram: Visual representations, such as diagrams or charts, can help clarify relationships between different parts of the problem and make the solution process clearer.
- Work backwards: If the problem is difficult to approach from start to finish, sometimes working backwards from the solution can provide insights.
- Use estimation: When exact solutions are challenging, estimating values or approximating can help guide the overall problem-solving process.
By adopting a methodical approach to word problems, students can improve their ability to translate real-world situations into solvable mathematical equations. Whether simple or complex, word problems can be tackled with practice and the right strategies.
How to Check Your Solutions for Accuracy
Ensuring that your solutions are correct is an essential step in problem-solving. It’s easy to make small mistakes during calculations, so verifying your results is crucial. This section outlines practical techniques for checking your work to ensure its accuracy before finalizing your solution. With careful review and the use of different methods, you can avoid common errors and gain confidence in your solutions.
Methods for Verifying Solutions
There are several effective ways to verify that your solutions are correct. Below are some of the most reliable approaches:
- Substitute the solution back: The most straightforward way to check if your solution is accurate is to substitute your result back into the original equation or problem. If both sides of the equation balance, your solution is correct.
- Estimate the result: Before finalizing your answer, make an estimate of the expected result. If your solution is far off from the estimated value, it’s likely you made an error somewhere in your process.
- Use an alternative method: If possible, solve the problem using a different approach or technique. If both methods lead to the same result, your solution is likely correct.
- Double-check your steps: Review each step of your solution process to identify any miscalculations or skipped steps that could lead to an incorrect answer.
Common Mistakes to Look Out For

Even with careful attention, some mistakes are easy to overlook. Being aware of common errors can help you catch them in time:
| Common Mistakes | How to Avoid |
|---|---|
| Incorrect arithmetic operations | Check each calculation step carefully, especially when adding or subtracting large numbers. |
| Sign errors | Pay attention to positive and negative signs throughout the process, particularly when multiplying or dividing. |
| Misinterpretation of the problem | Read the problem multiple times to ensure you fully understand the question and what is being asked. |
| Skipping intermediate steps | Write out all steps clearly. Skipping steps can lead to missing crucial details and errors in the final solution. |
By incorporating these methods into your problem-solving routine, you can ensure that your answers are accurate and reliable. Whether it’s through substitution, estimation, or reviewing each step, checking your work is an indispensable skill in any mathematical or problem-solving endeavor.
Improving Problem-Solving Skills in Mathematics
Enhancing your ability to solve problems effectively is a key skill in any learning process. This section provides strategies and techniques to strengthen your approach to problem-solving. By understanding various methods, practicing regularly, and developing a strategic mindset, you can significantly improve your ability to tackle challenges more confidently and efficiently.
Effective Strategies for Problem Solving
There are several approaches that can help improve your problem-solving skills. Here are some practical techniques to incorporate into your practice:
- Understand the problem thoroughly: Before jumping into calculations, take time to fully comprehend the problem. Identify what is being asked, the data provided, and any relationships between variables.
- Break it down into smaller steps: Complex problems can often seem overwhelming. By breaking them down into manageable parts, you can approach each step systematically and reduce errors.
- Use visualization: Drawing diagrams or charts can help you better understand relationships and see patterns that may not be immediately obvious in text alone.
- Look for patterns: Many problems have underlying patterns that can simplify the solution. Identifying these can save time and lead to more efficient strategies.
- Work backward: In some cases, solving the problem in reverse can reveal important steps that might be missed when working forward from the given information.
The Importance of Regular Practice
Like any skill, problem-solving improves with regular practice. The more problems you solve, the more familiar you become with common techniques, patterns, and types of challenges. In addition to practicing regularly, it’s important to review your work, identify areas for improvement, and apply new strategies as you learn them.
By committing to consistent practice and refining your problem-solving strategies, you’ll develop a deeper understanding of concepts and enhance your ability to approach any problem with confidence.
Using Online Resources to Boost Learning
The digital age has revolutionized the way students approach learning. Online platforms offer a wealth of tools and materials that can greatly enhance understanding and retention of key concepts. Whether you are looking to supplement your studies, find additional practice problems, or explore different teaching methods, the internet provides an abundance of resources that cater to diverse learning needs.
Online tutorials, interactive problem sets, video lessons, and discussion forums allow learners to engage with content in multiple ways, ensuring a deeper grasp of difficult topics. With instant access to a variety of teaching styles and explanations, students can find the methods that resonate best with them, enabling more effective learning.
Furthermore, digital resources make learning more flexible and accessible. You can study at your own pace, revisit complex topics, and use different platforms that offer personalized feedback and assessments. By integrating online tools into your study routine, you can maximize your learning potential and accelerate your progress.
How to Prepare for Transition Math Exams
Preparing for exams in this field requires a structured approach to reinforce your knowledge and ensure you’re confident with the material. The key is to develop effective study habits that focus on both understanding the concepts and practicing problem-solving techniques. Here are some strategies to help you succeed:
- Review Key Concepts: Go over the fundamental ideas and formulas that are central to the subject. Understanding these will serve as the foundation for solving more complex problems.
- Practice Regularly: Consistent practice is crucial. Work through problems from previous exams or textbooks to reinforce your understanding. The more problems you solve, the more prepared you will be for the test.
- Understand the Format: Familiarize yourself with the exam structure. Knowing whether the test consists of multiple-choice questions, short answers, or long-form problems will help you manage your time effectively.
In addition to the above strategies, it’s important to seek help if you’re struggling with specific topics. Don’t hesitate to ask questions during class, or use online resources to get further explanations. Group study sessions can also be beneficial as they allow you to exchange ideas and solve problems collaboratively.
Finally, make sure to give yourself enough time to prepare. Start early, break your study sessions into manageable chunks, and take regular breaks to stay fresh and focused. By staying organized and proactive, you’ll be well on your way to mastering the material and succeeding in your exams.
Building Confidence in Learning Math
Gaining confidence in problem-solving and understanding mathematical concepts is crucial for long-term success. When you feel secure in your ability to tackle challenges, your performance improves, and the subject becomes more enjoyable. The key to developing self-assurance in this area is consistent practice, a positive mindset, and using strategies that build your understanding step by step.
Effective Approaches to Strengthen Confidence
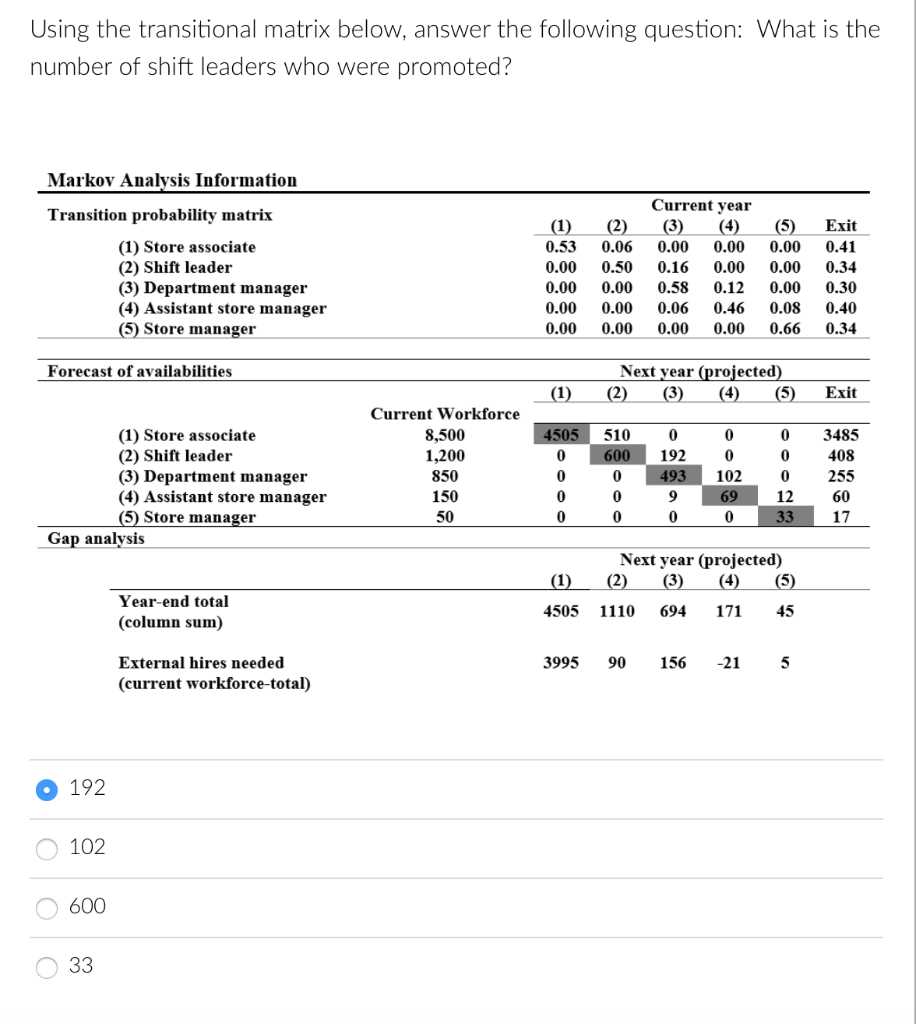
- Start with the Basics: Begin by mastering fundamental concepts before moving on to more complex topics. A solid grasp of the basics will provide a strong foundation for more challenging problems.
- Embrace Mistakes: Don’t be afraid to make errors. Mistakes are an important part of the learning process. Analyze them, learn from them, and use them as stepping stones to improve.
- Break Problems into Smaller Steps: Instead of feeling overwhelmed by large problems, break them down into manageable parts. Solve each part individually to make the task feel less intimidating.
Building a Positive Mindset
- Celebrate Small Wins: Each time you solve a problem or understand a new concept, take a moment to acknowledge your achievement. This boosts your confidence and motivates you to continue.
- Stay Consistent: Regular practice is essential. The more you practice, the more comfortable you will become with different types of problems.
- Stay Persistent: Building confidence takes time. If you don’t get something right away, keep going. Persistence will lead to improvement.
By using these methods, you’ll gradually build confidence and transform your approach to learning. Over time, you’ll find that the subject becomes less daunting, and you’ll be able to approach challenges with a sense of ease and determination.