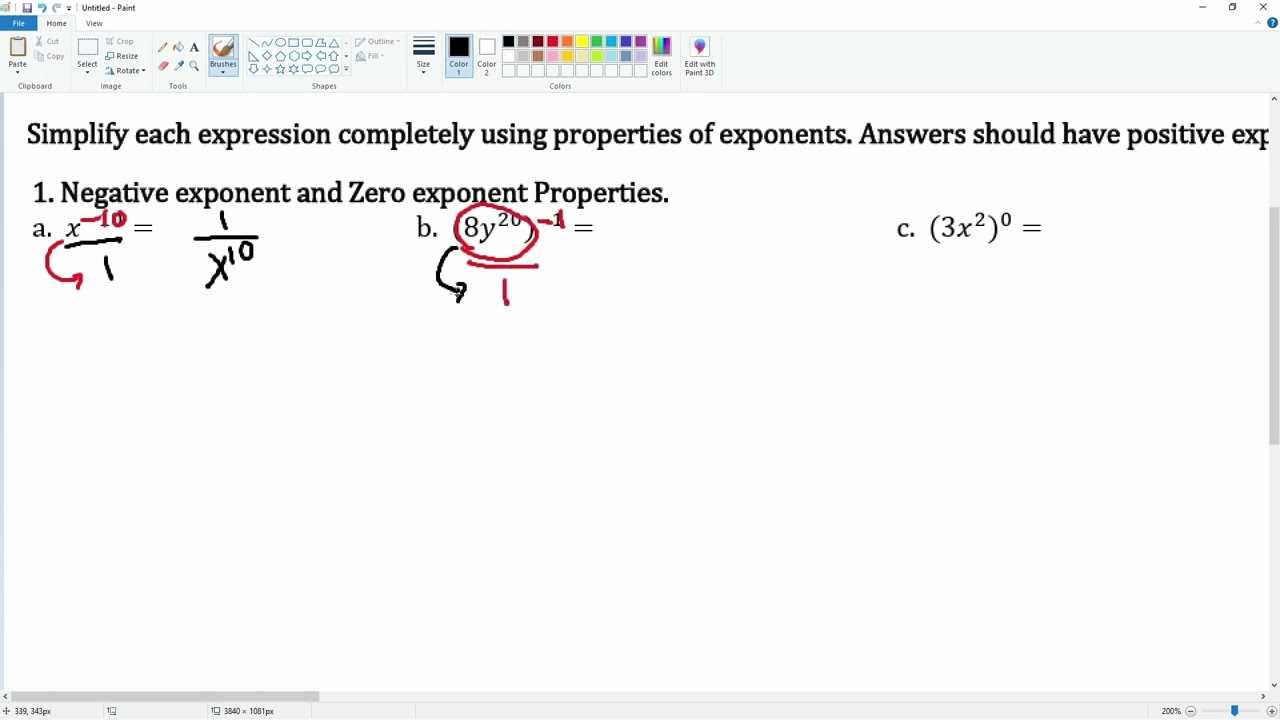
Understanding the fundamental principles of mathematics is essential for progressing in problem-solving and analysis. This section focuses on various techniques and methods that are crucial for tackling more advanced tasks. By mastering these core skills, learners can gain confidence and improve their ability to handle complex exercises.
Step-by-step guidance will help you navigate through the challenges, ensuring clarity in each solution. With a clear focus on simplifying problems and applying strategies effectively, you can approach even the most intricate topics with ease. Whether dealing with equations, functions, or other essential concepts, this guide will equip you with the knowledge needed to succeed.
By delving deeper into problem-solving strategies, you will find that the process becomes more intuitive. As you progress, applying these techniques will lead to greater mastery and a deeper understanding of mathematical reasoning.
Understanding Key Solutions and Strategies
This section focuses on the essential solutions and methods required to master the material covered in the current unit. By breaking down complex problems into simpler steps, you can develop a clear understanding of the techniques used to find the correct outcomes. Each problem-solving strategy will help you grasp the underlying principles and build a solid foundation for more advanced topics.
Step-by-step approaches are provided to guide you through various exercises, allowing you to see how solutions unfold logically. By applying these methods, you will be able to handle a wide range of scenarios with confidence. Whether it’s simplifying expressions or solving equations, these strategies will enable you to tackle any problem efficiently.
As you work through the examples, you’ll gain the insight needed to identify common challenges and avoid frequent mistakes. Mastery of these key concepts will not only improve your skills but also give you the confidence to approach future exercises with ease.
Key Concepts Covered in Chapter 7
In this section, we explore the fundamental ideas and principles that are crucial for mastering the current unit. These concepts provide the foundation for tackling more advanced problems and developing a deeper understanding of the material. By focusing on these core elements, you will strengthen your ability to approach different mathematical challenges effectively.
- Solving linear equations with multiple variables
- Understanding systems of equations and their solutions
- Exploring the relationship between variables through graphs
- Factoring expressions and recognizing patterns
- Working with inequalities and their graphical representations
These key ideas will help you break down complex problems and develop logical methods for finding solutions. Mastery of these concepts is essential for building confidence in more advanced topics.
Understanding Algebraic Expressions in Review
This section focuses on how to work with and interpret mathematical expressions, which are fundamental for solving various types of problems. By recognizing the components of an expression and how they relate to one another, you can simplify and manipulate them more easily. Understanding these building blocks is essential for progressing to more complex topics and challenges.
| Expression | Terms | Operations |
|---|---|---|
| 3x + 4y – 7 | 3x, 4y, -7 | Addition, Subtraction |
| 5a – 2b + c | 5a, -2b, c | Subtraction, Addition |
| 6x² + 3y – 12 | 6x², 3y, -12 | Multiplication, Addition |
By analyzing the structure of these expressions, you can gain a clearer understanding of how to simplify them and solve for unknown values. This knowledge forms the foundation for tackling more intricate equations and challenges in future studies.
Step-by-Step Solutions for Practice Problems
This section offers a detailed approach to solving mathematical problems by breaking them down into manageable steps. Each example is designed to help you understand the process and apply the correct techniques to find the solution. By following these steps, you will learn how to approach similar problems with confidence and clarity.
Starting with simple examples, each solution walks you through the necessary calculations and logic. This structured approach ensures that you understand how to move from one step to the next, making complex problems more accessible. By practicing these steps, you will develop the skills to solve increasingly challenging exercises.
Common Mistakes in Algebra Chapter 7
When solving mathematical problems, it’s easy to overlook certain steps or make simple errors that can lead to incorrect results. This section highlights some of the most frequent mistakes students make when working through the exercises. Understanding these pitfalls will help you avoid them and improve your problem-solving skills.
Incorrectly Simplifying Expressions
One of the most common mistakes is mishandling the simplification of expressions, particularly when combining like terms or applying distributive properties. It’s important to double-check each step to ensure that terms are properly grouped and coefficients are correctly adjusted.
Misunderstanding the Order of Operations
Another common issue arises when the order of operations is not followed correctly. Skipping steps or performing operations in the wrong order can lead to incorrect solutions. Remember to always work through parentheses, exponents, multiplication and division, and addition and subtraction in the proper sequence.
Tips for Solving Equations Effectively
Solving equations can often feel challenging, but with the right approach, you can simplify the process and achieve accurate results. This section offers practical advice to help you tackle different types of equations more efficiently. By following these strategies, you’ll develop a clearer understanding and gain confidence in your problem-solving abilities.
Break Down the Problem Step-by-Step
It’s essential to approach each equation by breaking it down into smaller, more manageable parts. Start by isolating the variable, then perform operations methodically. Taking it one step at a time reduces the risk of making errors and ensures that each part of the equation is addressed properly.
Double-Check Your Work
After solving an equation, always review your steps to ensure accuracy. This includes checking the arithmetic and verifying that you’ve followed the correct order of operations. A quick review can help catch any mistakes that might have been overlooked in the process.
How to Simplify Complex Expressions
Simplifying complex expressions is a crucial skill that helps to make complicated mathematical problems more manageable. By applying a few key techniques, you can break down an expression into a simpler form, making it easier to solve. This process involves recognizing patterns, combining like terms, and using fundamental mathematical properties.
Identify Like Terms and Combine Them
One of the first steps in simplifying an expression is to look for like terms, which are terms that have the same variable and exponent. Once identified, these terms can be combined by adding or subtracting their coefficients.
Use Distribution to Eliminate Parentheses
If the expression includes parentheses, apply the distributive property to eliminate them. Multiply each term inside the parentheses by the factor outside to simplify the expression further.
| Expression | Simplified Form |
|---|---|
| 3x + 4x | 7x |
| 2(x + 5) | 2x + 10 |
| 4a + 3a – 2b | 7a – 2b |
By consistently applying these strategies, you can efficiently simplify even the most complex expressions, making them easier to solve and understand.
Analyzing Graphs and Functions in Chapter 7
Understanding the relationship between equations and their graphical representations is essential for solving many mathematical problems. In this section, we explore how to interpret graphs and functions, identifying key features that reveal important information about the data. By analyzing these elements, you can gain deeper insights into the behavior of mathematical relationships.
Identifying Key Features of Graphs
When analyzing a graph, focus on its key characteristics, such as intercepts, slopes, and asymptotes. These features provide valuable information about the function’s behavior and help you understand how the equation is represented visually.
Understanding the Shape of Functions
Each type of function has a distinct shape that can be identified on a graph. Recognizing these patterns allows you to make predictions and draw conclusions about the function’s values and behavior in different regions of the graph.
Mastering Systems of Equations
Solving systems of equations is an essential skill for tackling problems that involve multiple variables. By understanding the different methods for solving these systems, you can approach a wide range of problems with confidence. Whether you choose substitution, elimination, or graphing, each method has its own advantages depending on the problem.
- Substitution method: Solving one equation for a variable and substituting it into the other equation.
- Elimination method: Adding or subtracting equations to eliminate one variable and solve for the other.
- Graphing method: Plotting both equations on a graph to find their point of intersection.
Each technique has its place, and by practicing them, you’ll become proficient in solving systems of equations. With time, you’ll develop the ability to quickly identify the best method for each situation, making the process more efficient and accurate.
Exploring Quadratic Equations and Solutions
Quadratic equations are a fundamental part of mathematics, often appearing in various fields. These equations typically involve a variable raised to the second power and can be solved in several ways. Understanding the different approaches to solving them is crucial for solving a wide range of problems that model real-world situations.
- Factoring: Finding factors of the equation that allow for the solution to be derived directly.
- Completing the square: Rewriting the equation in a perfect square form to easily solve for the variable.
- Quadratic formula: Using the standard formula to find the roots of any quadratic equation.
Each method offers a unique way to approach quadratic equations, depending on the form of the equation and the desired result. By practicing these techniques, you’ll become adept at solving quadratic problems and understanding the behavior of the functions they represent.
Solving Word Problems with Algebra
Word problems are a common way to apply mathematical concepts to real-life scenarios. They can seem challenging at first, but with a systematic approach, they become much easier to tackle. The key to solving these types of problems lies in translating the given information into mathematical expressions or equations, and then solving them step by step.
Identify the Known and Unknown Variables

Start by carefully reading the problem and identifying the known and unknown quantities. Assign variables to the unknowns and express the relationships between these variables based on the information provided in the problem.
Set Up an Equation and Solve
Once the variables are identified, the next step is to set up an equation that represents the situation. Use appropriate operations to solve for the unknowns, and check your solution by substituting the values back into the original context of the problem.
Real-World Applications of Algebraic Concepts

Mathematical concepts are not just theoretical; they are actively used to solve problems in the real world. From budgeting and construction to engineering and technology, the skills learned in this subject can be applied to a variety of fields. Understanding how to manipulate equations and analyze relationships is essential for addressing practical challenges.
Applications in Finance
One of the most common uses of mathematical concepts is in managing personal and business finances. For example:
- Budgeting: Setting up equations to calculate expenses, savings, and income over time.
- Loan calculations: Using equations to determine interest rates, monthly payments, and the total amount paid over time.
Applications in Engineering and Design
In engineering, mathematics is used to model and solve problems related to structures, forces, and materials. Some uses include:
- Structural analysis: Using mathematical models to ensure that buildings and bridges can withstand loads and forces.
- Optimization: Finding the most efficient designs for products, systems, or processes by solving equations that model different variables.
By applying these concepts, real-world problems can be solved more efficiently, saving time and resources while ensuring optimal outcomes. Whether in finance, engineering, or technology, the ability to solve and manipulate equations is invaluable in nearly every professional field.
Reviewing Inequalities and Their Solutions
Inequalities are an essential part of mathematics, used to represent situations where values are not equal but have a range of possible outcomes. Understanding how to solve and interpret inequalities is crucial for comparing quantities and understanding the relationships between them. These solutions often lead to ranges or intervals of values rather than exact numbers, providing flexibility in problem-solving.
Types of Inequalities
Inequalities come in different forms, each representing a different relationship between values. Some common types include:
- Less than ( Represents a value that is smaller than another value.
- Greater than (>): Indicates a value that is larger than another value.
- Less than or equal to (≤): Includes values that are less than or exactly equal to another value.
- Greater than or equal to (≥): Represents values that are greater than or exactly equal to another value.
Solving and Graphing Inequalities
Solving inequalities often follows similar steps to solving equations, but with some key differences. The main challenge is ensuring that when multiplying or dividing by negative numbers, the inequality sign is reversed. After solving, the solutions are typically represented on a number line or in interval notation to show the possible range of values.
Preparing for Chapter 7 Test and Exam
Preparing for a test or exam requires a strategic approach, especially when the material covers a wide range of topics. Focusing on key concepts and practicing problem-solving skills will help you approach the test with confidence. This section will guide you on how to effectively study and review the material to ensure success during your assessment.
Effective Study Strategies
To prepare efficiently, it’s important to focus on the most critical areas of the material. Here are a few strategies that can help:
- Review key concepts: Go over the main ideas and formulas to ensure you understand the foundations.
- Practice problems: Work through a variety of problems to familiarize yourself with different question types.
- Use study guides: Utilize practice exams or worksheets to test your knowledge under timed conditions.
- Seek help if needed: If you’re struggling with certain concepts, don’t hesitate to ask for clarification from a teacher or tutor.
Time Management and Test-Taking Tips
Effective time management during the exam is crucial for completing all sections. Here are some helpful tips for managing your time and maximizing your performance:
- Read instructions carefully: Take the time to understand each question before answering.
- Start with familiar questions: Begin with the problems you find easiest to build confidence and gain momentum.
- Allocate time wisely: Ensure that you spend an appropriate amount of time on each section, leaving time for review.
- Check your work: If time allows, review your answers to catch any mistakes.
Helpful Study Strategies for Chapter 7
Effective studying is key to mastering any set of mathematical concepts. To excel in the upcoming assessment, it’s important to employ a combination of review techniques and active practice. This section will highlight practical strategies that can help you efficiently study and improve your understanding of the material.
To get the most out of your study time, consider using the following techniques:
| Study Strategy | Benefits |
|---|---|
| Active Problem Solving | Helps reinforce concepts through practice and improves problem-solving speed. |
| Creating Flashcards | Facilitates memorization of key formulas and steps for quick recall. |
| Explaining Concepts Out Loud | Improves comprehension by teaching the material to others or yourself. |
| Group Study Sessions | Encourages collaboration, allowing for discussion of difficult topics and different approaches. |
| Breaks and Time Management | Prevents burnout by allowing time to rest and refocus between study periods. |
By combining these strategies, you can better retain the information and approach your exam with confidence. Regular practice and consistent review will ensure you’re prepared to tackle any problem that comes your way.
Commonly Asked Questions About Algebra 1
As students progress through mathematical concepts, certain questions often arise that need further clarification. In this section, we address some of the most frequently asked inquiries to help deepen understanding and provide clarity on common challenges encountered in problem-solving and theory.
How do I solve linear equations?
To solve a linear equation, isolate the variable by performing inverse operations. Start by eliminating constants from both sides of the equation, then simplify and solve for the variable. Make sure to check your solution by substituting it back into the original equation.
What is the best way to handle negative numbers?

When dealing with negative numbers, always remember the rule of signs. When adding or subtracting, combine the values based on their signs. For multiplication and division, remember that two negative numbers give a positive result, while a negative and a positive yield a negative result.
Why do we use parentheses in expressions?
Parentheses are used to indicate which operations should be performed first. They help clarify the order of operations and ensure that calculations are carried out correctly. Always simplify expressions inside parentheses before moving to other operations like multiplication or division.
What is factoring, and why is it important?
Factoring is the process of breaking down an expression into its simpler components, or factors, that can be multiplied to form the original expression. This technique is important for solving quadratic equations and simplifying expressions, and it is a fundamental skill for advanced problem-solving.
By addressing these questions and reinforcing core concepts, students can gain a stronger grasp of the material, leading to greater success in solving problems and understanding key principles.