
Preparing for a challenging assessment in advanced mathematics can seem overwhelming, but with the right approach, you can boost your confidence and performance. This section is designed to help you navigate through the most crucial topics that are likely to appear in your upcoming test. By focusing on the core principles and essential skills, you’ll be able to tackle various problems with ease.
Effective preparation requires a clear understanding of the concepts that form the foundation of the subject. Whether you’re grappling with complex equations, functions, or advanced operations, reviewing the material systematically will ensure you grasp each topic thoroughly. Emphasizing problem-solving techniques and practice will prepare you for any challenge.
Success in this area depends on recognizing patterns and applying learned strategies to different types of questions. By revisiting key topics, reviewing step-by-step methods, and practicing under timed conditions, you’ll feel well-equipped to handle all the questions in your test with clarity and precision.
Algebra 2 Semester Exam Review Answers
Mastering key mathematical concepts is essential for performing well in tests covering advanced topics. The following section focuses on addressing the most commonly tested areas and offers a structured approach to help you understand the material deeply. By breaking down complex problems into manageable steps, you’ll gain the confidence to solve similar questions on your own.
Core Concepts to Focus On
Understanding the fundamental building blocks is crucial for tackling higher-level problems. The main areas you should focus on include:
- Solving equations and inequalities
- Working with functions and their properties
- Graphing and analyzing different types of curves
- Manipulating polynomials and rational expressions
- Exploring sequences and series
Step-by-Step Problem-Solving Approach
To succeed in solving problems, it’s important to follow a systematic approach:
- Read the problem carefully and identify key information.
- Choose the appropriate method or formula to apply.
- Break down the problem into smaller parts if necessary.
- Verify your solution by substituting it back into the original problem.
- Practice similar problems to reinforce your understanding.
By focusing on these strategies and revisiting important topics regularly, you’ll be well-prepared to confidently approach any challenge in your test.
Key Topics to Focus On
When preparing for a challenging assessment in advanced mathematics, it’s important to focus on the core topics that are most likely to appear. Understanding these areas will provide you with the necessary skills to solve a wide range of problems. By mastering these concepts, you’ll be able to apply your knowledge efficiently and confidently during the test.
Critical Areas for Success
To perform well, make sure you thoroughly understand the following concepts:
- Solving linear and quadratic equations
- Identifying and working with functions and their graphs
- Manipulating exponents and radicals
- Understanding systems of equations and inequalities
- Working with rational expressions and polynomials
- Analyzing sequences and series
- Exploring exponential and logarithmic relationships
Tips for Mastery
Focusing on the following strategies can help you tackle these areas with ease:
- Practice solving problems step-by-step for better retention
- Understand the underlying principles rather than memorizing formulas
- Review common problem types to become familiar with the structure
- Test your understanding through mock problems or practice sets
By concentrating on these key areas and using these strategies, you’ll be well-equipped to handle the most challenging questions and excel in your test.
Important Formulas for Algebra 2
In advanced mathematics, understanding and memorizing essential formulas is crucial for solving various types of problems quickly and accurately. These formulas are the foundation for a wide range of topics, from solving equations to graphing functions. Having a solid grasp of these key equations will help you approach questions with confidence and efficiency.
Below are some of the most important formulas you should be familiar with:
Key Equations for Problem Solving
- Quadratic Formula: x = (-b ± √(b² – 4ac)) / 2a
- Distance Formula: d = √((x₂ – x₁)² + (y₂ – y₁)²)
- Slope Formula: m = (y₂ – y₁) / (x₂ – x₁)
- Standard Form of a Line: Ax + By = C
- Pythagorean Theorem: a² + b² = c²
Exponential and Logarithmic Relationships
- Exponential Growth/Decay: A = P(1 ± r)ⁿ
- Logarithmic Conversion: logₐ(b) = x ⟺ aˣ = b
Be sure to practice applying these formulas to various types of problems. Understanding how and when to use each equation will greatly improve your problem-solving skills and allow you to tackle challenges with greater ease.
How to Solve Quadratic Equations
Solving quadratic equations is a fundamental skill in mathematics that helps in understanding the relationships between variables and their graphs. These equations typically involve a variable raised to the second power, and they appear in many real-world applications. There are various methods for solving these types of equations, and selecting the right one depends on the specific problem.
Here are the most common techniques for solving quadratic equations:
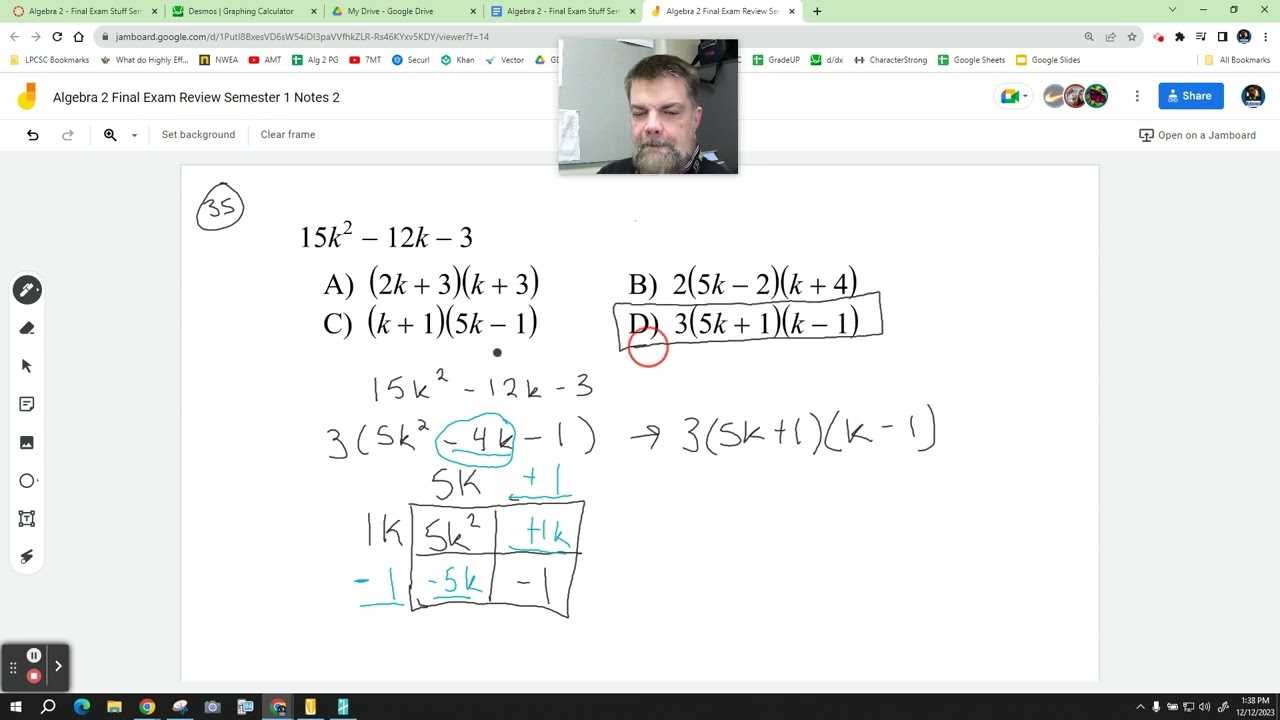
- Factoring: If the equation can be factored, this method involves breaking down the quadratic expression into two binomials and solving for the variable.
- Quadratic Formula: When factoring is difficult, the quadratic formula provides a reliable way to find the roots. The formula is x = (-b ± √(b² – 4ac)) / 2a.
- Completing the Square: This method involves rewriting the equation as a perfect square trinomial and then solving for the variable.
- Graphing: For a visual approach, graphing the equation helps to find the points where the parabola intersects the x-axis, representing the solutions.
Each method has its advantages depending on the given equation. Understanding when and how to use each method will enhance your ability to solve these equations accurately and efficiently.
Understanding Functions and Their Graphs
Functions are key to understanding how variables relate to each other in mathematical problems. A function describes a relationship where every input corresponds to exactly one output. The graphical representation of a function is just as important, as it allows you to visualize the behavior of the relationship. By analyzing these graphs, you can uncover important properties, such as intercepts, slopes, and symmetry.
Graphs provide a visual way to explore the properties of a function, and each type of function has a characteristic shape. For example, linear functions produce straight lines, while quadratic functions form parabolas. Recognizing the general shape of a function’s graph can help you predict the solutions and understand its behavior across different intervals.
Key aspects to examine when studying graphs:
- Intercepts: The points where the graph crosses the x-axis and y-axis.
- Domain and Range: The set of possible input values (domain) and the corresponding output values (range).
- Slope: For linear functions, the slope indicates how steep the line is and the direction in which it moves.
- Symmetry: Certain functions, like even or odd functions, exhibit symmetry across specific axes.
By studying the function’s graph, you can quickly identify key features and gain deeper insight into its behavior, making it easier to solve related problems.
Reviewing Systems of Equations
Systems of equations involve finding the values of multiple variables that satisfy two or more equations simultaneously. These problems appear frequently in advanced mathematical studies and real-world scenarios. Solving these systems requires strategies that simplify the process and ensure the most accurate solutions are found. Understanding how to approach these problems is essential for tackling a variety of related topics.
Methods for Solving Systems
There are several methods to solve systems of equations, each suitable for different types of problems:
- Substitution: Solve one equation for one variable and substitute the result into the other equation.
- Elimination: Add or subtract the equations to eliminate one variable, making it easier to solve for the other.
- Graphing: Graph both equations and identify the point(s) of intersection, which represent the solution(s).
Example Problem
Consider the following system:
| Equation 1 | Equation 2 |
|---|---|
| 2x + 3y = 6 | 4x – y = 7 |
To solve this system, you could use the substitution method or elimination method. The point where both equations intersect on a graph will give you the solution.
By mastering these techniques, you will be able to solve any system efficiently and accurately, whether the equations are linear, nonlinear, or involve multiple variables.
Polynomials and Their Operations
Polynomials are mathematical expressions consisting of variables raised to different powers, combined with constants through addition, subtraction, and multiplication. They play a crucial role in many areas of mathematics, and understanding how to manipulate them is essential for solving a wide range of problems. The operations performed on these expressions, such as addition, subtraction, multiplication, and division, follow specific rules that can simplify complex expressions and lead to more manageable forms.
Key Operations with Polynomials
Here are the most common operations you will encounter when working with polynomials:
- Addition and Subtraction: Combine like terms by adding or subtracting their coefficients.
- Multiplication: Multiply each term of one polynomial by each term of the other. Use the distributive property (FOIL method) to simplify.
- Division: Polynomial division can be performed using long division or synthetic division to simplify the expression.
Example of Polynomial Operations
For instance, consider the following polynomials:
- Polynomial 1: 3x² + 2x – 5
- Polynomial 2: 2x² – 4x + 3
To add these polynomials, you would combine like terms:
- (3x² + 2x – 5) + (2x² – 4x + 3) = 5x² – 2x – 2
Mastering these operations is essential for simplifying expressions, solving equations, and working with higher-level problems in mathematics.
Solving Inequalities in Algebra 2
Inequalities express relationships where one side is not necessarily equal to the other but is greater than, less than, or comparable to it. Solving these problems requires a similar approach to solving equations, but with additional rules that apply when multiplying or dividing by negative numbers. Understanding how to handle these differences is essential for accurately finding the solution set and graphing the result.
Key steps to solving inequalities:
- Isolate the variable: Just like in equations, begin by moving all terms involving the variable to one side and constants to the other side.
- Apply operations: Use addition, subtraction, multiplication, or division to simplify the inequality, remembering to reverse the inequality sign when multiplying or dividing by a negative number.
- Graph the solution: Once you have the solution, you can represent it on a number line to visualize the possible values for the variable.
Example: Solve the inequality -3x + 5 ≥ 11:
- Subtract 5 from both sides: -3x ≥ 6
- Divide by -3 (and reverse the inequality sign): x ≤ -2
The solution is x ≤ -2, which means that any value of x less than or equal to -2 will satisfy the inequality.
By practicing these techniques, you’ll develop a deeper understanding of how to solve inequalities efficiently and correctly, preparing you for more complex mathematical challenges.
Understanding Rational Expressions
Rational expressions are fractions where the numerator and the denominator are both polynomials. These expressions are fundamental in various mathematical contexts, and mastering how to work with them is crucial for solving complex problems. Operations with rational expressions, such as simplifying, multiplying, dividing, adding, and subtracting, involve specific rules that differ from basic arithmetic fractions.
Key concepts to remember when working with rational expressions:
- Simplification: Always factor both the numerator and the denominator to identify and cancel out common factors.
- Multiplication and Division: When multiplying rational expressions, multiply the numerators and denominators separately. For division, multiply by the reciprocal of the second expression.
- Addition and Subtraction: To add or subtract rational expressions, find a common denominator, and then combine the numerators.
Example of Simplifying a Rational Expression
Consider the expression (x² – 4) / (x² + 2x – 8) . To simplify:
- Factor both the numerator and the denominator:
- (x² – 4) = (x – 2)(x + 2)
- (x² + 2x – 8) = (x – 2)(x + 4)
- The expression becomes: (x – 2)(x + 2) / (x – 2)(x + 4)
- Cancel out the common factor (x – 2): (x + 2) / (x + 4)
The simplified form of the rational expression is (x + 2) / (x + 4).
By following these procedures, you can manipulate rational expressions effectively, which is vital for solving more advanced mathematical problems and equations.
Exponents and Exponential Functions
Exponents are a fundamental concept in mathematics that represent repeated multiplication of a number by itself. These operations are essential when working with both simple and complex equations. Exponential functions take this concept further, involving variables in the exponent position. Understanding how to manipulate and work with these forms allows for solving a wide range of real-world problems, such as growth and decay, as well as more advanced mathematical expressions.
Key Properties of Exponents:
- Product Rule: When multiplying terms with the same base, add the exponents. For example, a^m × a^n = a^(m+n).
- Power Rule: When raising a term to a power, multiply the exponents. For example, (a^m)^n = a^(m×n).
- Quotient Rule: When dividing terms with the same base, subtract the exponents. For example, a^m ÷ a^n = a^(m-n).
Understanding Exponential Functions
Exponential functions are of the form f(x) = a × b^x, where a is a constant, b is the base, and x is the exponent. These functions model a variety of real-world phenomena such as population growth, radioactive decay, and financial interest. When the base b > 1, the function shows growth; when 0 , it shows decay.
Example of an Exponential Function
Consider the exponential function f(x) = 2 × 3^x. Let’s calculate the values for different values of x:
| x | f(x) = 2 × 3^x |
|---|---|
| 0 | 2 × 3^0 = 2 |
| 1 | 2 × 3^1 = 6 |
| 2 | 2 × 3^2 = 18 |
| 3 | 2 × 3^3 = 54 |
As shown, the value of f(x) increases exponentially as x increases, demonstrating rapid growth.
Mastering exponents and exponential functions is key to advancing in mathematics, as they are commonly applied in various fields such as finance, science, and engineering.
Logarithmic Equations and Solutions
Logarithmic equations involve expressions where the unknown appears in the exponent. These types of equations are commonly encountered in various fields such as physics, finance, and engineering. Solving logarithmic equations requires understanding the inverse relationship between logarithms and exponentials. By applying specific rules and properties, one can isolate the variable and find the solution to these equations.
Steps for Solving Logarithmic Equations:
- Isolate the Logarithmic Expression: Begin by isolating the logarithmic term on one side of the equation. This allows for easier manipulation.
- Rewrite the Logarithmic Equation in Exponential Form: Use the definition of a logarithm to rewrite the equation as an exponential equation. For example, logb(x) = y becomes b^y = x.
- Solve the Exponential Equation: Once in exponential form, solve for the variable by applying appropriate algebraic techniques.
- Check for Extraneous Solutions: Logarithmic equations can sometimes result in extraneous solutions that do not satisfy the original equation. Always substitute your solution back into the original equation to check for validity.
Example of Solving a Logarithmic Equation
Consider the equation log2(x + 3) = 4. To solve:
- Isolate the logarithmic expression: log2(x + 3) = 4.
- Rewrite in exponential form: 2^4 = x + 3.
- Simplify: 16 = x + 3.
- Solve for x: x = 16 – 3 = 13.
The solution to the equation is x = 13. Always check that the solution does not result in taking the logarithm of a negative number or zero, as this is undefined.
By understanding and practicing these steps, you can effectively solve logarithmic equations and apply them to a variety of mathematical problems.
Matrix Operations and Applications
Mathematical matrices are powerful tools used to represent and solve systems of linear equations, perform transformations, and model a variety of real-world situations. The operations that can be performed on matrices include addition, subtraction, multiplication, and finding the determinant or inverse of a matrix. Each operation has specific rules, and understanding these rules is essential to working with matrices effectively. These concepts have wide applications in fields like computer graphics, economics, engineering, and data science.
Key Matrix Operations:
- Matrix Addition and Subtraction: Matrices of the same size can be added or subtracted by performing element-wise addition or subtraction.
- Matrix Multiplication: Matrix multiplication involves multiplying rows of the first matrix by columns of the second matrix. This operation is not commutative, meaning AB ≠ BA in most cases.
- Finding the Determinant: The determinant of a square matrix provides important information, such as whether the matrix is invertible. It can be computed using specific formulas depending on the size of the matrix.
- Inverse of a Matrix: If a matrix has an inverse, it can be used to solve systems of linear equations and find solutions to other matrix problems. The inverse of a matrix A is denoted as A-1.
Applications of Matrices
Matrices are used in a variety of real-world applications. Below are some of the common areas where matrices play an essential role:
- Computer Graphics: Matrices are used to perform transformations on images, such as rotations, translations, and scaling, in digital graphics and video games.
- Cryptography: In encryption methods, matrices are used to encode and decode messages securely.
- Economic Modeling: Matrices are used in economics to model systems of linear equations representing supply and demand, production costs, and other economic variables.
- Data Analysis: In machine learning and statistics, matrices are used to store data sets and perform operations such as regression analysis and classification.
By mastering the operations of matrices and understanding their applications, you can tackle complex problems across many disciplines, from theoretical mathematics to practical real-world scenarios.
Conic Sections in Algebra 2
Conic sections are a set of curves that can be derived by intersecting a plane with a double cone. These shapes appear frequently in various fields, including physics, astronomy, and engineering, due to their unique properties and applications. The primary conic sections are circles, ellipses, parabolas, and hyperbolas. Each has distinct characteristics and equations that describe their geometric properties.
Understanding the equations and the graphical representation of these curves is key to solving a variety of problems. By studying conic sections, one can explore topics such as the relationship between focus points and directrix, eccentricity, and the general form of conic equations. These concepts are foundational to many advanced topics in mathematics and applied sciences.
Types of Conic Sections:
- Circle: A circle is a set of all points in a plane equidistant from a fixed point, called the center. Its equation is typically written as (x – h)² + (y – k)² = r², where (h, k) represents the center, and r is the radius.
- Ellipse: An ellipse is a set of points where the sum of the distances to two fixed points (the foci) is constant. Its equation takes the form (x – h)²/a² + (y – k)²/b² = 1, where a and b are the lengths of the semi-major and semi-minor axes.
- Parabola: A parabola is a curve that is symmetric and defined by a point called the focus and a line called the directrix. Its equation can be expressed as y = a(x – h)² + k or x = a(y – k)² + h, depending on the orientation of the parabola.
- Hyperbola: A hyperbola is a set of points where the difference of the distances to two fixed points (the foci) is constant. Its equation is typically written as (x – h)²/a² – (y – k)²/b² = 1, where a and b relate to the distances between the vertices and the asymptotes.
These curves not only have a deep theoretical significance but also have practical uses in fields ranging from satellite communication to the design of parabolic reflectors. By mastering the study of conic sections, students can gain valuable skills for analyzing geometric patterns and solving complex equations.
Working with Sequences and Series
Sequences and series are essential concepts in mathematics that allow us to explore patterns and relationships between numbers. A sequence is an ordered list of numbers, where each term follows a specific rule or pattern. When we add the terms of a sequence together, we obtain a series. Understanding how to manipulate and analyze sequences and series is critical for solving a wide range of mathematical problems, especially those related to growth, decay, and pattern recognition.
There are two main types of sequences that are frequently studied: arithmetic and geometric. In an arithmetic sequence, the difference between consecutive terms is constant, while in a geometric sequence, each term is found by multiplying the previous term by a constant factor.
Arithmetic Sequences: The general form of an arithmetic sequence is given by the equation: aₙ = a₁ + (n – 1)d, where aₙ is the nth term, a₁ is the first term, n is the number of terms, and d is the common difference.
Geometric Sequences: In a geometric sequence, the nth term is calculated by aₙ = a₁ * r^(n – 1), where r is the common ratio between successive terms.
When working with series, it’s important to know the formulas for the sum of both arithmetic and geometric series. These sums are useful in various applications, such as calculating total amounts in finance, physics, and computer science.
Formulas for the Sum of a Series:
- Arithmetic Series: The sum of the first n terms of an arithmetic series can be found using the formula: Sₙ = n/2 * (2a₁ + (n – 1)d), where Sₙ is the sum, n is the number of terms, a₁ is the first term, and d is the common difference.
- Geometric Series: The sum of the first n terms of a geometric series is given by: Sₙ = a₁ * (1 – rⁿ) / (1 – r), where r is the common ratio, and a₁ is the first term.
Understanding how to work with sequences and series opens up a wide range of problem-solving techniques. By mastering these concepts, students are better prepared to handle more advanced mathematical challenges and apply these principles to real-world scenarios.
Example Problem:
| Sequence Type | Formula | Example Calculation |
|---|---|---|
| Arithmetic | aₙ = a₁ + (n – 1)d | Find the 10th term of the sequence: 5, 8, 11, … |
| Geometric | aₙ = a₁ * r^(n – 1) | Find the 5th term of the sequence: 3, 6, 12, … |
Exploring Probability and Statistics
Understanding how to analyze data and predict outcomes is a crucial skill in many fields, from business and economics to science and engineering. Probability and statistics are branches of mathematics that deal with uncertainty and the interpretation of data. By exploring these concepts, we can make informed decisions, identify patterns, and assess the likelihood of events occurring.
Probability helps us quantify the likelihood of various outcomes in uncertain situations. It involves calculating the chances of an event happening, based on possible outcomes. Statistics, on the other hand, focuses on collecting, analyzing, and interpreting data to draw meaningful conclusions. Both areas are deeply connected, as probability provides the foundation for statistical inference, helping to understand and make predictions based on data.
Key Concepts in Probability:
- Sample Space: The set of all possible outcomes of an experiment.
- Event: A specific outcome or set of outcomes from a sample space.
- Probability of an Event: The ratio of the number of favorable outcomes to the total number of outcomes in the sample space. It is expressed as P(E) = Number of favorable outcomes / Total number of outcomes.
- Complementary Events: The probability that an event does not occur is the complement of the event. P(not E) = 1 – P(E).
Basic Concepts in Statistics:
- Mean: The average of a set of numbers, calculated by summing all the values and dividing by the number of values.
- Median: The middle value in a set of ordered data, or the average of the two middle values if the data set has an even number of terms.
- Mode: The value that appears most frequently in a data set.
- Standard Deviation: A measure of the amount of variation or dispersion in a set of data values.
These concepts form the backbone of statistical analysis, helping us summarize data, calculate risks, and make predictions about future events. In practice, probability and statistics are used to understand trends, make decisions under uncertainty, and model real-world situations. Mastery of these topics is invaluable for analyzing data sets, conducting surveys, and making evidence-based decisions in various fields.
Example Problem:
| Concept | Formula | Example Calculation |
|---|---|---|
| Probability | P(E) = Number of favorable outcomes / Total number of outcomes | What is the probability of rolling a 3 on a fair six-sided die? |
| Mean | Mean = (Sum of all values) / (Number of values) | Find the mean of the set {4, 7, 10, 13}. |
Tips for Time Management During Exams
Managing your time effectively during a test is crucial for success. Proper time allocation ensures that you can complete all sections of the assessment without rushing or leaving questions unanswered. By following some strategic steps, you can optimize your performance, reduce stress, and make the most of the available time.
1. Plan Ahead

Before starting the test, take a few minutes to review the entire paper. This will help you gauge the difficulty of each section and allocate time accordingly. Prioritize questions that you find easier or are worth more points. Having a mental map of the test can help you navigate it more efficiently.
2. Set Time Limits for Each Section
Divide the total time available by the number of sections or questions. This will give you a general idea of how much time you should spend on each part. Stick to these time limits to ensure you don’t spend too much time on one question and neglect others. If you’re stuck on a question, move on and return to it later if time permits.
3. Stay Calm and Focused
It’s easy to become overwhelmed during a test, but staying calm is essential. If you feel yourself getting anxious, take a deep breath and refocus. Trust in your preparation, and remember that it’s about doing your best within the time constraints, not rushing through the material.
4. Use Spare Time Wisely
If you finish early, use the remaining time to double-check your answers. Look for mistakes or questions you might have skipped. A quick review can help you catch simple errors and improve your score.
By managing your time effectively, you can approach the test with confidence and maximize your chances of success.