
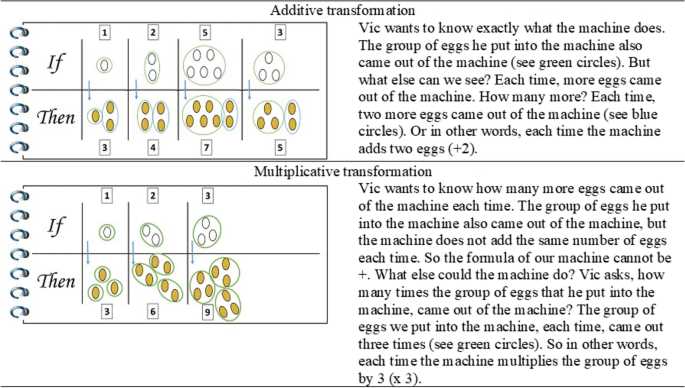
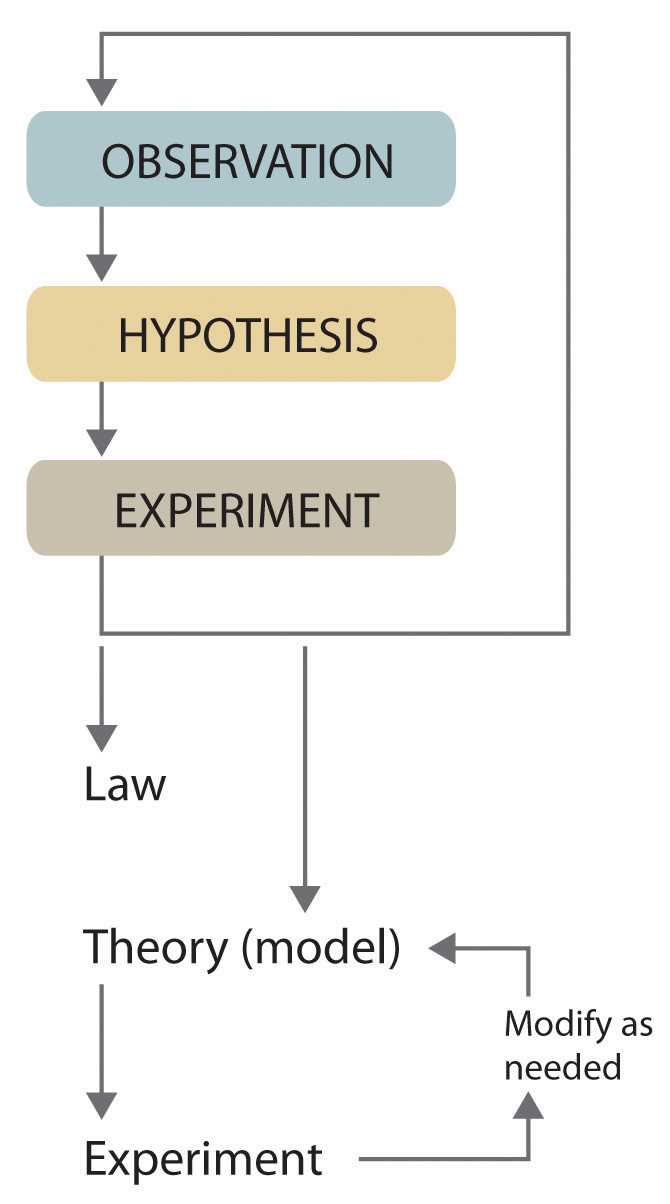
In the realm of solving mathematical and logical challenges, mastering the relationship between quantities is essential. The ability to identify how different elements are connected and apply this understanding to find solutions is a fundamental skill. By examining various exercises and problems, one can develop a clearer sense of how to approach complex tasks systematically.
Grasping the connections between values allows for better predictions and more accurate calculations in both everyday situations and academic scenarios. This approach enables individuals to break down difficult concepts into manageable steps, making it easier to solve a wide range of questions that may appear overwhelming at first.
In this section, we focus on enhancing your ability to tackle problems that involve relationships between different quantities. With practice, you will be able to apply these techniques confidently, improving both your problem-solving skills and your overall understanding of numerical interactions.
Scientific Methods Worksheet 2 Proportional Reasoning Answers
This section focuses on solving mathematical challenges that involve the relationship between different variables. By identifying how one value changes in relation to another, it’s possible to predict outcomes and solve problems with greater accuracy. Developing the skill to recognize these patterns can significantly enhance problem-solving abilities in various contexts, from basic calculations to more complex scenarios.
Identifying Key Relationships in Problems
To solve problems involving varying quantities, it’s important to first recognize the key relationships at play. Whether dealing with simple fractions or more advanced equations, understanding how one element influences another is the foundation for finding the correct solution. By breaking down the problem into smaller parts, you can isolate the connections that are critical to solving the puzzle.
Practical Applications and Problem Solving
Once the relationships between variables are identified, the next step is applying this knowledge to solve real-life problems. These concepts are not limited to theoretical exercises; they are used daily in fields ranging from engineering to economics. By practicing these techniques, you can improve your ability to tackle a wide range of issues, both in academic exercises and in practical situations.
Understanding Proportional Reasoning Basics
At the core of many mathematical and logical challenges lies the ability to compare and connect different quantities. Recognizing how changes in one factor can affect another is essential for solving a wide range of problems. This concept forms the foundation for understanding complex relationships and making accurate predictions based on given data.
By learning to identify patterns and ratios between numbers, individuals can simplify and solve problems more efficiently. Whether dealing with scaling, adjusting measurements, or solving word problems, mastering this skill enables better analysis and decision-making in various fields, from science to everyday life.
Key Concepts in Proportional Relationships

Understanding the connections between different quantities is essential for solving many types of problems. Recognizing how one factor changes in relation to another allows for better predictions and more efficient calculations. These relationships are fundamental in fields ranging from basic arithmetic to advanced scientific studies.
Here are some key concepts to grasp when working with these types of challenges:
- Ratios: The comparison of two numbers that shows the relative size of one compared to the other.
- Scaling: Adjusting one quantity in direct relation to another, maintaining the same ratio between them.
- Unit Rates: The ratio of one quantity to a single unit of another, often used to measure efficiency or speed.
- Cross-Multiplication: A method used to solve equations involving ratios or fractions by multiplying across the terms.
- Constant Change: When the ratio between two quantities remains unchanged despite variations in their individual values.
Grasping these basic ideas helps in applying the right strategies to solve problems where two or more quantities are linked. By practicing these concepts, you can improve your ability to analyze data, make predictions, and solve real-world challenges efficiently.
Step-by-Step Guide to Solving Problems
Solving complex challenges often requires a structured approach. Breaking down the problem into manageable steps allows for better clarity and helps identify the most effective solutions. By following a systematic process, you can tackle even the most intricate problems with confidence and precision.
Identify the Key Elements
The first step in solving any problem is to identify the critical information. Look for the variables involved, the relationships between them, and the goal you are aiming to achieve. Understanding the context of the problem will help you choose the right approach and tools for solving it.
Apply the Appropriate Method
Once the key elements are identified, the next step is to apply the most suitable technique. Whether it involves simple arithmetic, algebra, or more advanced strategies, using the right method is crucial to reaching an accurate solution. Always double-check your calculations and assumptions to ensure everything aligns with the problem’s requirements.
Examples of Proportional Reasoning in Science
In many scientific fields, the relationship between different quantities plays a crucial role in understanding natural phenomena and conducting experiments. By recognizing how changes in one variable impact another, scientists can make predictions, test hypotheses, and draw conclusions based on observed data. These concepts are frequently applied in various areas of research and experimentation.
1. Dilution in Chemistry: When preparing solutions, the concentration of a substance is often diluted by mixing it with a solvent. The ratio of solute to solvent must remain consistent to achieve the desired concentration. For example, if a chemist dilutes a solution by a factor of 2, they know that the amount of solute will decrease proportionally while the volume of the solvent increases.
2. Speed and Distance in Physics: The relationship between speed, time, and distance is a fundamental concept in physics. When studying motion, scientists use ratios to calculate how far an object will travel in a given time based on its speed. For example, if an object travels 60 meters in 2 minutes, it is traveling at a rate of 30 meters per minute, a linear relationship that can be applied to other scenarios.
3. Population Growth in Biology: In ecological studies, the growth rate of a population often follows a predictable pattern. If the number of individuals in a population increases at a constant rate, this growth can be modeled using ratios. For example, if a population doubles every year, the relationship between time and population size is proportional, allowing for future predictions.
Common Mistakes in Proportional Calculations
When working with relationships between different quantities, it’s easy to make errors that can lead to incorrect conclusions. These mistakes often arise from misunderstandings or misapplications of basic principles. By recognizing the most common pitfalls, you can avoid errors and improve the accuracy of your calculations.
- Ignoring Units: One of the most frequent mistakes is failing to keep track of units throughout the calculation. Always ensure that units match or are converted properly before performing operations.
- Misinterpreting Ratios: Ratios are a comparison of two values, but it’s important to understand what each number represents. Confusing which value is the numerator and which is the denominator can lead to incorrect results.
- Overlooking Constant Relationships: Sometimes, it’s assumed that variables change independently, when in reality, they are linked in a constant way. Failing to recognize this can result in inaccurate conclusions.
- Forgetting to Scale Properly: In many cases, it’s necessary to scale one value relative to another. Forgetting to apply the correct factor or miscalculating the scale can lead to errors in predictions or solutions.
- Overcomplicating the Problem: It’s easy to become overwhelmed and overthink a problem. Often, the simplest approach–using basic principles–can lead to the correct answer. Avoid the temptation to make things more complicated than they need to be.
By being aware of these common mistakes, you can refine your approach to problem-solving and avoid some of the most common pitfalls in calculations involving variable relationships.
Strategies for Mastering Proportions
Mastering the ability to work with relationships between quantities takes practice and a solid understanding of key principles. By using the right techniques and practicing regularly, you can enhance your problem-solving skills and improve your ability to work with numerical relationships. Below are some effective strategies to help you master these concepts.
- Understand the Core Concepts: Before diving into more complex problems, make sure you fully understand the basic principles of ratios and relationships between numbers. Start with simple examples to build a solid foundation.
- Use Visuals: Visual aids like tables, charts, and graphs can help you better understand how values change in relation to one another. Visualizing data often makes it easier to identify patterns and relationships.
- Practice Cross-Multiplication: Cross-multiplication is a powerful tool when solving equations that involve ratios. Practicing this technique will help you solve problems more quickly and accurately.
- Work with Real-World Examples: Apply the concepts you learn to real-life situations, such as cooking recipes, budgeting, or measuring materials. This helps reinforce the practical use of these relationships and enhances your understanding.
- Check Your Work Regularly: After completing a calculation, always review your work to make sure all the steps are correct. Double-checking your answers helps to avoid simple errors that can lead to incorrect results.
By following these strategies and applying them consistently, you can develop a strong grasp of working with relationships between quantities, allowing you to tackle increasingly complex problems with confidence and accuracy.
How to Interpret Word Problems Correctly

Interpreting word problems accurately is essential for solving them effectively. Often, these problems contain all the necessary information, but it is up to you to extract and organize it correctly. With the right approach, you can turn the information in the problem into a solvable equation or relationship.
Steps to Interpreting Word Problems
- Read the Problem Carefully: Begin by reading the problem slowly and thoroughly. Ensure you understand the overall scenario before looking for specific details.
- Identify the Key Information: Identify the important numbers, quantities, and relationships mentioned in the problem. Pay close attention to units and how the variables interact with each other.
- Highlight Important Terms: Mark or underline key phrases such as “per”, “total”, “increased by”, or “divided by”. These terms often indicate mathematical operations that guide the solution process.
- Determine What You Are Asked to Find: Clearly define what the problem is asking for. Are you solving for a total, a rate, or an unknown quantity? Knowing this helps focus your approach.
- Translate Words into Mathematical Expressions: Convert the key relationships into mathematical terms, such as fractions, ratios, or equations. This step is crucial for setting up the problem properly.
Common Pitfalls to Avoid
- Overlooking Units: Always ensure that units of measurement (like meters, hours, or dollars) are consistent throughout the problem. Ignoring or mixing units can lead to errors.
- Misunderstanding Word Choices: Phrases like “twice as much” or “per unit” can be easily misinterpreted. Ensure you understand the specific meaning of such terms before proceeding.
- Rushing Through the Problem: Take your time to understand the structure and logic behind the question. Rushing can cause you to miss critical details.
By following these steps and being mindful of common mistakes, you can develop a clearer approach to interpreting word problems, leading to more accurate solutions and a deeper understanding of the relationships at play.
Practical Applications of Proportions in Science
In various scientific fields, understanding the relationships between different quantities is essential for conducting experiments, making predictions, and analyzing results. These relationships often follow a consistent pattern, which can be used to solve real-world problems. By applying these principles, scientists are able to develop accurate models and solutions to complex questions in biology, chemistry, physics, and beyond.
Here are a few examples of how these concepts are applied in different scientific disciplines:
| Field | Application | Example |
|---|---|---|
| Biology | Population Growth | The number of organisms in a population increases or decreases in a predictable way based on a constant rate. |
| Chemistry | Solution Concentration | When mixing substances to create a solution, the concentration of the solute can be calculated by understanding the ratio of solute to solvent. |
| Physics | Speed and Distance | In motion studies, the relationship between speed, time, and distance is often used to predict how far an object will travel in a given amount of time. |
| Ecology | Resource Distribution | The distribution of resources in an environment, like food or water, often follows a proportional pattern to the population’s needs. |
These are just a few examples of how proportional relationships help scientists model, test, and solve problems across a variety of disciplines. By understanding these relationships, scientists can make more accurate predictions and develop effective solutions in their respective fields.
Visualizing Proportional Relationships with Graphs
One of the most effective ways to understand the connection between two variables is by graphing their relationship. Graphs provide a clear and immediate visual representation that can make it easier to identify trends, patterns, and correlations. In many scientific and mathematical contexts, visualizing data can help clarify complex ideas and reveal insights that might not be obvious from raw numbers alone.
The Benefits of Graphing Data

- Clarity: Graphs can simplify complex data, making it easier to interpret and understand at a glance. By plotting points and connecting them, you can quickly see how one variable affects another.
- Pattern Recognition: With graphs, it’s easier to detect trends or relationships between variables. Whether the relationship is linear or non-linear, a graph will show you the connection more clearly than words or equations alone.
- Comparing Data: Graphs allow you to compare multiple sets of data simultaneously, which is especially useful when analyzing experiments with different variables or conditions.
Types of Graphs Used in Scientific Analysis
- Line Graphs: Line graphs are commonly used to represent continuous data, showing how one variable changes in relation to another over time or in response to changes in a different variable.
- Bar Graphs: Bar graphs are effective for comparing discrete categories or showing data that is grouped in specific intervals, making them useful for comparisons across different experiments or groups.
- Scatter Plots: Scatter plots are often used to show individual data points, allowing you to examine the correlation between two variables more closely.
By using graphs to visualize relationships, you can gain a deeper understanding of how changes in one variable may affect another. Whether in scientific research, engineering, or other fields, graphs are an invaluable tool for analyzing and communicating data.
How to Check Your Answers Effectively
Reviewing your solutions is a crucial step in ensuring the accuracy and reliability of your work. By checking your calculations and logic carefully, you can avoid common mistakes and confirm that your conclusions are correct. A systematic approach to verifying your results not only improves the quality of your answers but also helps you develop stronger problem-solving skills.
Steps to Verify Your Solutions
- Double-check calculations: Revisit each calculation step and verify that the numbers are correct. It is easy to make simple arithmetic mistakes, so reviewing every operation helps ensure accuracy.
- Check units: Ensure that all units are consistent throughout your solution. Mismatched units can lead to incorrect conclusions, so always check that conversions have been made properly.
- Compare with known results: If possible, compare your results with previously known or expected values. This can help you quickly identify any discrepancies or errors in your process.
Common Techniques for Verification
- Reversing the Process: Sometimes, retracing your steps in reverse order can help you spot errors that were made earlier in the problem-solving process.
- Cross-checking with Different Methods: Try solving the same problem using a different approach or formula. If the results match, this can help confirm the validity of your solution.
- Seeking Peer Review: Ask a colleague or classmate to check your work. A fresh set of eyes can often spot mistakes that you may have missed.
Taking the time to verify your solutions in multiple ways not only helps improve the accuracy of your work but also strengthens your problem-solving techniques. With practice, checking your work will become an automatic and essential part of the process.
Real-World Problems Involving Proportions
Many everyday situations require the use of ratios and comparisons to solve practical problems. These relationships often involve understanding how two quantities relate to one another in a consistent way. From cooking recipes to financial planning, recognizing and working with these connections can simplify decision-making and improve our ability to handle various tasks efficiently.
One common example is adjusting a recipe for different serving sizes. If a recipe is designed for four people but you need to prepare it for eight, you would double the ingredients to maintain the same taste and consistency. This type of adjustment is based on a proportional relationship where the increase in servings is directly proportional to the increase in ingredient quantities.
Another example can be found in everyday shopping. When purchasing multiple items, understanding unit price can help you make smarter choices. For instance, if one product offers 10 ounces for $5 and another offers 15 ounces for $6, you can use proportions to determine which product gives you more value for your money by comparing the unit prices.
Additionally, proportions are essential in fields such as engineering, medicine, and construction. Whether determining the right dosage of medicine based on body weight or scaling up a blueprint to fit a new size, proportions provide a straightforward way to apply known ratios to new circumstances.
By recognizing proportional relationships in daily life, we can make more informed decisions, save time, and better manage resources. Understanding how these connections work is not only useful in academics but also practical in real-world scenarios.
Impact of Proportions on Scientific Experiments
In research and experimentation, understanding how different variables relate to each other is essential for drawing accurate conclusions. The ability to manipulate and calculate these relationships can drastically affect the outcomes of experiments. Whether testing a hypothesis or analyzing data, the use of ratios and relationships helps maintain consistency and validity in experimental design.
One significant impact of ratios in experiments is in the preparation of solutions and mixtures. For instance, when creating chemical solutions, the concentration of a substance must be precisely measured. A slight deviation in the ratio of ingredients can lead to faulty results or even hazardous conditions. By maintaining correct proportions, researchers ensure that the experimental setup is accurate and reliable.
In biological experiments, proportions are crucial for things like calculating dosages for medications or studying growth rates. For example, when measuring the effect of a drug on different species, the correct ratio of dosage to body weight must be used to ensure the results are consistent and applicable to the population under study.
Furthermore, proportions are often used to scale experiments from small models to larger systems. For instance, when designing a prototype for a new technology, researchers often use smaller-scale models and scale up the results based on established proportional relationships. This technique allows for more manageable and cost-effective testing before full-scale implementation.
Ultimately, the accurate application of proportions allows researchers to eliminate variables that might skew results and ensures that their findings are both reproducible and valid across different conditions. Mastery of these relationships is critical for producing meaningful and trustworthy scientific data.
Solving Complex Problems Using Proportions
When faced with intricate problems in various fields, breaking them down into simpler, manageable components can help find the solution. One effective way to approach these challenges is by recognizing and applying relationships between quantities. These relationships can provide a clear path to solving problems that initially appear overwhelming or complicated. By using appropriate comparisons, we can simplify complex situations into something more tractable.
For instance, in fields like engineering or architecture, scaling is a common issue that requires the application of basic relationships. When creating a smaller model of a large structure, understanding how to properly scale dimensions is essential. A small mistake in determining the correct ratio can lead to inaccurate results and potential structural failures. With careful attention to the ratios, designers and engineers can ensure the model accurately represents the real-world object.
Example: Scaling a Building Model
Consider a scenario where an architect needs to create a scaled model of a building. If the building’s height is 100 meters and the model is scaled down by a ratio of 1:100, the height of the model will be calculated as follows:
| Actual Height (meters) | Scale Ratio | Model Height (meters) |
|---|---|---|
| 100 | 1:100 | 1 |
In this example, the proportion helps ensure that every part of the model is proportionally smaller than the actual building, maintaining accuracy throughout the design process.
Example: Adjusting Ingredients for Cooking
Another common example is adjusting recipe quantities when preparing food for a different number of people. For instance, if a recipe is designed for 4 servings but needs to be adjusted for 10 servings, the ingredients must be multiplied by a ratio of 10:4 (or 5:2). By maintaining this ratio for each ingredient, the proportions of the ingredients stay consistent, ensuring the final dish tastes as expected, even when scaled up.
These examples demonstrate how applying ratios allows us to navigate complex challenges, making otherwise difficult problems more manageable. Whether it’s designing models, scaling experiments, or adjusting everyday tasks, recognizing proportional relationships offers a straightforward path to finding accurate solutions.
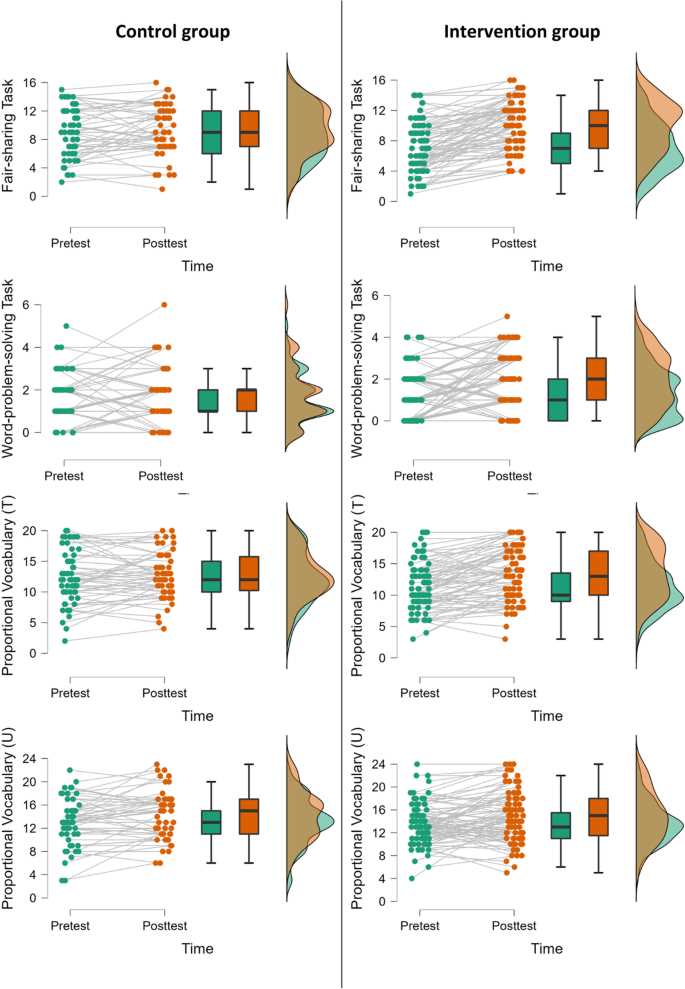
Using Proportional Reasoning in Data Analysis

In the world of data analysis, understanding the relationships between different sets of values is crucial. Often, these relationships are represented as ratios or comparisons, which allow analysts to draw meaningful conclusions from complex data. By leveraging these connections, analysts can identify trends, make predictions, and uncover insights that would be difficult to see through raw numbers alone. The ability to recognize and apply such relationships is key to making data-driven decisions in fields ranging from business to healthcare.
For instance, in market research, businesses often compare sales data from different regions to understand patterns in consumer behavior. These comparisons might involve examining how the growth rate of one product category relates to the overall market trend. By applying simple ratios, analysts can quantify these relationships and use them to forecast future sales or identify areas for improvement.
Example: Analyzing Sales Growth
Suppose a company wants to assess the growth rate of a new product over three months. The sales data for each month is provided, and the goal is to calculate the monthly growth rate. Using a ratio of the current month’s sales to the previous month’s sales, we can easily find the percentage growth for each month.
| Month | Sales ($) | Growth Rate |
|---|---|---|
| January | 5000 | – |
| February | 6000 | +20% |
| March | 7200 | +20% |
In this example, the growth rate is calculated by dividing the current month’s sales by the previous month’s sales and then multiplying by 100 to get the percentage. This simple approach helps to identify consistent growth trends and make predictions about future sales.
Another common application is in evaluating healthcare data. For instance, if a researcher wants to analyze the effectiveness of a medication, they might compare the recovery rate of patients in different treatment groups. By using ratios, they can determine if one treatment is more effective than another and quantify the difference in a meaningful way.
In summary, proportional relationships are essential tools for data analysis, providing a clear and efficient way to draw connections between numbers. Whether comparing sales figures, evaluating performance, or analyzing experimental outcomes, recognizing and using ratios can help to unlock valuable insights and guide better decision-making.
Tips for Improving Your Proportional Skills
Developing a strong understanding of numerical relationships can significantly improve your ability to analyze and solve problems involving comparisons or ratios. Whether you’re working with data, interpreting statistics, or simply looking to improve your math skills, mastering this area of mathematics is essential. By applying a few strategies and practicing regularly, you can enhance your ability to interpret and solve such problems with ease.
1. Practice with Real-World Examples
The best way to improve your skills is through hands-on practice. Start by analyzing everyday situations where numerical relationships are present. For instance, consider the amount of ingredients needed when adjusting a recipe. If a recipe calls for 2 cups of flour for 4 servings, how much flour is needed for 6 servings? These types of problems, while simple, help to reinforce the concepts of comparing quantities and making adjustments based on changes in one variable.
2. Use Visual Aids to Understand Concepts
Graphs, tables, and charts can be extremely helpful in visualizing relationships between numbers. By converting ratios and relationships into visual formats, you can gain a clearer understanding of how different values are connected. Drawing simple diagrams, such as bar charts, can help you spot trends and relationships that may not be immediately obvious from raw numbers alone. Using visual tools can make the problem-solving process feel more intuitive.
3. Break Problems into Smaller StepsWhen confronted with a complex problem, it’s easy to feel overwhelmed. Instead of tackling everything at once, break the problem down into smaller, more manageable parts. Start by identifying the known values and what needs to be calculated. Then, apply simple operations such as multiplication, division, or addition to find the solution. This approach not only makes problems easier to solve but also boosts your confidence.
4. Learn and Apply Key FormulasFamiliarize yourself with essential formulas that are often used to solve ratio and proportion problems. For instance, the formula for calculating a ratio is:
Ratio = (part) / (whole)
By understanding these key formulas, you will be able to approach problems more effectively and solve them quickly.
Improving your ability to work with numerical relationships requires time and consistent practice. Whether through solving real-life examples, using visual tools, or applying key formulas, each of these strategies will strengthen your skills and help you tackle more complex problems with confidence.