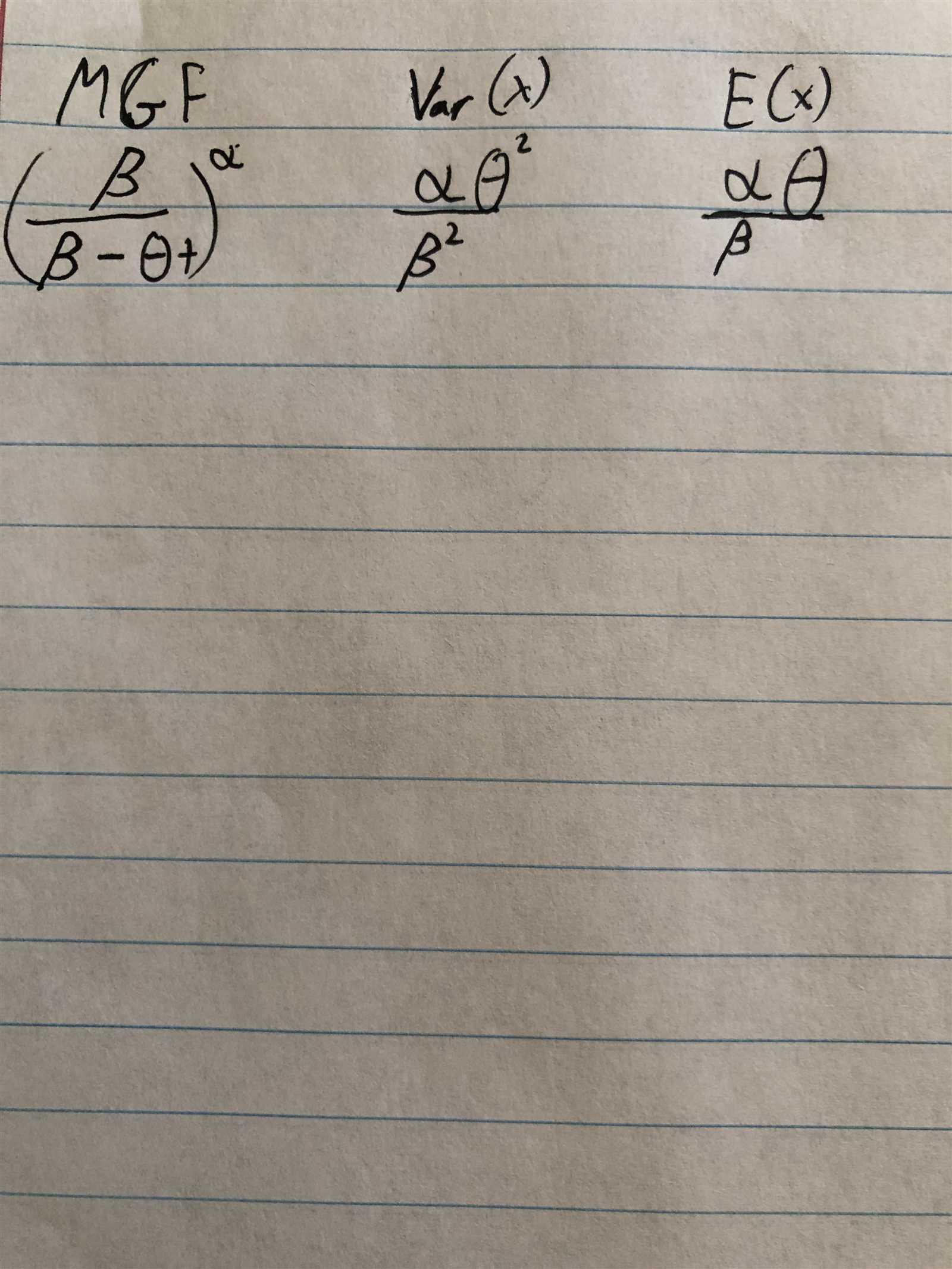Preparing for a challenging assessment in the field of risk management and statistics requires a solid understanding of key principles. To help streamline the process, candidates often rely on a condensed reference guide that outlines the most critical equations and concepts needed for solving problems efficiently. This resource serves as an invaluable tool, offering quick access to vital calculations during practice and while tackling questions.
The right approach involves not just memorizing essential values, but also understanding how to apply them effectively under pressure. Familiarizing yourself with this guide allows for quicker decision-making, reducing the time spent on calculations and improving overall performance. While a thorough grasp of the underlying concepts is necessary, having a reference for quick verification can significantly enhance confidence and reduce anxiety when faced with complex problems.
Understanding the Actuary Exam P Formula Sheet
In any rigorous assessment, having a concise yet comprehensive guide to rely on can make a significant difference. A well-structured reference document provides an overview of the essential calculations, allowing you to focus on problem-solving rather than memorizing lengthy equations. This resource is carefully designed to support individuals in managing complex tasks under time constraints, making it an indispensable tool during preparation and actual performance.
The reference guide for this particular test contains a selection of key mathematical principles, from probability concepts to statistical techniques. These principles, presented in a clear and accessible format, help candidates navigate the various question types with confidence. Understanding how to use this document effectively can streamline the process and save valuable time.
- Key Probability Distributions: Understanding and applying the basic distributions, such as binomial and normal, is crucial for quick calculations.
- Common Statistical Methods: Methods like expected value, variance, and standard deviation are foundational to problem-solving.
- Conditional Probability: Grasping conditional relationships between events is essential for many types of questions.
By becoming familiar with these elements, you can increase your efficiency and minimize errors. Having a clear grasp of the material presented in the guide is not just about memorization, but about knowing when and how to apply each concept correctly. With regular practice, you will become adept at navigating the guide and using it to your advantage when tackling even the most challenging questions.
What is the Actuary Exam P?
This particular assessment is a critical milestone for individuals pursuing a career in risk management and statistical analysis. It is designed to test knowledge in key mathematical areas, focusing on probability theory and its application to real-world problems. Success in this evaluation signifies a solid understanding of the foundational principles that guide many analytical roles in the financial and insurance industries.
The evaluation primarily involves understanding how to model uncertain events, calculate probabilities, and apply various statistical methods to assess risk and make informed decisions. The ability to quickly and accurately use mathematical concepts is essential, as the test requires not only theoretical knowledge but also practical problem-solving skills.
Some key areas covered include:
- Basic Probability: The fundamentals of calculating the likelihood of events.
- Random Variables: Understanding different types and how they relate to real-world scenarios.
- Distributions: Knowledge of various probability distributions and their properties.
Given its importance in shaping a professional’s career, preparation for this assessment demands focused study and the ability to quickly recall essential information. Being well-versed in both the theory and its application under exam conditions is key to achieving success.
Importance of Formula Sheets in Actuary Exams
A reference guide is an essential tool during high-stakes assessments, especially when dealing with complex mathematical concepts and time-sensitive tasks. Having quick access to key equations and principles allows individuals to focus on applying their knowledge rather than recalling every detail under pressure. These resources significantly reduce the mental load, enabling candidates to efficiently solve problems and manage their time effectively.
Enhancing Accuracy and Efficiency
With the pressure of a limited time frame, it’s easy to make simple errors when performing intricate calculations. A well-organized reference tool helps minimize such mistakes, offering an opportunity for quick verification of equations and solutions. It allows for a smoother workflow, ensuring that the focus remains on the application of methods rather than on memorization.
Maximizing Time Management
Time management is crucial in any challenging test, and having a structured reference tool can save precious moments. Instead of spending unnecessary time recalling specific details or trying to rederive an equation, candidates can quickly refer to the guide to confirm their approach and move forward. This streamlined approach enables more efficient handling of each section and ensures a more balanced use of the available time.
Overall, such resources offer significant advantages in both boosting accuracy and optimizing time, ultimately contributing to a higher level of performance and confidence during the assessment process.
Key Concepts Covered in Exam P
The assessment focuses on a variety of fundamental concepts in probability and statistical theory. These principles form the core of many real-world applications, particularly in fields that involve risk management, data analysis, and forecasting. Understanding these core ideas is essential for making informed decisions based on statistical models and probabilistic calculations.
Some of the most important topics include:
- Probability Theory: Understanding the basics of probability, including independent and dependent events, conditional probability, and the law of total probability.
- Random Variables: A deep dive into the properties of random variables, their distributions, and how to calculate expectations and variances.
- Discrete and Continuous Distributions: Exploring key distributions such as binomial, normal, and exponential, and understanding their applications in real-world scenarios.
- Expected Value and Variance: The foundation of risk analysis, these concepts are crucial for evaluating and predicting outcomes based on probabilities.
By mastering these topics, candidates are equipped to solve complex problems related to uncertainty, making them capable of applying their knowledge to diverse situations where risk and probability play a role. Understanding these concepts thoroughly allows individuals to approach challenges with confidence and precision.
Common Formulas You Must Know

To succeed in any rigorous assessment, being familiar with essential calculations and their applications is crucial. Key mathematical expressions are used repeatedly throughout problem-solving, so knowing these by heart ensures quicker responses and greater accuracy. Below are some of the most commonly used equations that you should be comfortable with.
Basic Probability Calculations
Understanding the basic rules of probability is foundational. These calculations help determine the likelihood of events occurring and are used in many problem-solving scenarios.
| Formula | Description |
|---|---|
| P(A ∩ B) = P(A) * P(B|A) | Joint probability of two events A and B occurring together |
| P(A ∪ B) = P(A) + P(B) – P(A ∩ B) | Probability of either event A or event B occurring |
| P(A|B) = P(A ∩ B) / P(B) | Conditional probability of A given B |
Distributions and Expectations
Probability distributions describe how the probabilities are spread across different values, and understanding the expectations and variances helps in assessing outcomes.
| Formula | Description |
|---|---|
| E(X) = Σ [x * P(x)] | Expected value for a discrete random variable X |
| Var(X) = E(X^2) – (E(X))^2 | Variance of a random variable X |
| P(X = x) = (e^(-λ) * λ^x) / x! | Poisson distribution for a given event rate λ |
Familiarizing yourself with these key expressions is essential for handling a wide range of problems. Being able to recall them quickly and apply them effectively will improve your performance and enhance your problem-solving abilities.
How to Use the Formula Sheet Effectively
Having a reference guide during an assessment is a powerful tool, but it’s only useful if you know how to navigate it efficiently. The key to success lies not in merely having access to the material, but in understanding how and when to use it to save time and improve accuracy. Properly utilizing this resource can help streamline your problem-solving process, ensuring that you spend less time searching for information and more time applying your knowledge.
Here are some tips for making the most of your reference guide:
- Familiarize Yourself with the Layout: Before starting, take a few moments to get acquainted with the structure of the document. Knowing where key concepts and equations are located will allow you to quickly find what you need under time pressure.
- Know When to Refer to It: Don’t rely on the guide for every question. Use it to confirm your approach or for more complex calculations, but trust your preparation for simpler tasks. This balance helps save time.
- Practice Using It: During your study sessions, simulate test conditions by using the reference as if you were sitting for the real assessment. This practice will help you become quicker at finding the necessary information and applying it effectively.
Ultimately, the guide is there to assist, not to do the work for you. By knowing how to access and apply the information it contains efficiently, you’ll be able to solve problems with greater confidence and precision.
Strategies for Memorizing Key Formulas
Mastering essential mathematical expressions is a critical aspect of performing well in any assessment that tests analytical and problem-solving skills. While reference materials are available, having the ability to recall key equations from memory allows for quicker decision-making and a smoother process when tackling complex problems. Memorization strategies can help you retain this crucial information effectively and efficiently.
Use Mnemonics and Associations
One of the most effective ways to remember key equations is by using mnemonics or creating associations that link the formula to something familiar. This can be as simple as creating an acronym for the variables in the equation or imagining a real-world scenario where the formula would be applied. The more relatable and creative the connection, the easier it will be to recall the formula under pressure.
Practice Regularly and Actively
Active recall is one of the best techniques for solidifying information in your long-term memory. Instead of passively reading through the material, try to write down or verbally recall the formulas from memory. Repetition over time strengthens neural pathways and helps with faster retrieval. Additionally, incorporating practice problems into your study routine allows you to apply the formulas in context, reinforcing their importance and making the process more interactive.
By integrating these strategies into your study routine, you can effectively memorize the key mathematical expressions needed for success. Consistency and active engagement with the material will ensure that you retain the information and can confidently apply it when needed.
How the Formula Sheet Helps Time Management
Efficient time management is crucial during assessments that involve complex calculations and analysis. Having a quick-access resource that provides key mathematical expressions can significantly reduce the time spent searching for information or reworking equations. By knowing where to find important concepts, you can avoid unnecessary delays and focus on solving problems effectively within the given time frame.
Quick Access to Essential Information
When under pressure, every second counts. A well-organized reference guide allows you to quickly locate the necessary equations, saving time that would otherwise be spent remembering or deriving them from scratch. This reduces the mental effort required to recall specific details and helps you maintain focus on solving the task at hand.
- Reduced Cognitive Load: By minimizing the need to remember every detail, you free up cognitive resources to tackle more complex aspects of the problem.
- Faster Problem Solving: With immediate access to the correct calculations, you can quickly apply them, speeding up your problem-solving process.
- More Time for Review: By saving time on basic calculations, you can use any extra time to review your work and check for errors.
How to Maximize Efficiency
To make the most of this resource, it’s essential to practice using it in mock scenarios. Familiarizing yourself with the layout and knowing where to find key information will save even more time during the actual assessment. Additionally, using the guide selectively–only for complex or unfamiliar problems–ensures that you don’t rely on it for tasks you can solve from memory.
By incorporating a reference tool into your preparation, you can manage your time more effectively and ensure that you complete all tasks within the allotted period, reducing stress and boosting confidence.
Essential Probability Concepts for Exam P
In any rigorous assessment that involves statistical analysis, a solid understanding of probability is essential. Probability concepts form the foundation for many of the problems you’ll encounter, and being able to apply them quickly and accurately is key to success. These concepts help evaluate the likelihood of events occurring and are widely used in various problem-solving scenarios.
Key Probability Rules to Know
Understanding the basic principles of probability will serve as the building blocks for more advanced concepts. Here are some of the fundamental rules you should be familiar with:
- Probability of an Event: The probability of an event occurring is a number between 0 and 1, where 0 means the event will not occur, and 1 means it will definitely occur.
- Complementary Events: The probability that event A does not occur is 1 minus the probability that it does occur. Mathematically, P(A’) = 1 – P(A).
- Union of Events: The probability that either of two events A or B will occur is the sum of their individual probabilities minus the probability of both occurring together: P(A ∪ B) = P(A) + P(B) – P(A ∩ B).
Conditional Probability and Independence
These concepts are crucial when working with multiple events, as they help assess how the probability of one event is affected by the occurrence of another. Understanding how to calculate conditional probabilities and recognizing independent events can make a significant difference in problem-solving.
- Conditional Probability: The probability of an event A occurring given that event B has already occurred is P(A|B) = P(A ∩ B) / P(B).
- Independence of Events: Two events A and B are independent if the occurrence of one does not affect the probability of the other. Mathematically, P(A ∩ B) = P(A) * P(B).
Mastering these key probability concepts will provide the groundwork for tackling more complex problems effectively. They are not only important for assessments but also for real-world applications in various fields, from finance to risk management.
Practice Problems to Test Your Knowledge
One of the most effective ways to solidify your understanding of key concepts is through practice. By working through various problems, you can identify areas where you need improvement and gain confidence in your ability to apply your knowledge under time constraints. The following practice problems are designed to challenge your understanding of core principles and prepare you for more advanced scenarios.
Sample Problems for Probability and Statistics
- Problem 1: A fair coin is tossed three times. What is the probability that exactly two heads will appear?
- Problem 2: A deck of 52 playing cards is shuffled. What is the probability of drawing a red card or a face card?
- Problem 3: In a survey of 1000 people, 400 prefer coffee, 350 prefer tea, and 100 prefer both. What is the probability that a randomly chosen person prefers either coffee or tea?
Sample Problems for Understanding Distributions

- Problem 4: Given a normal distribution with a mean of 50 and a standard deviation of 10, calculate the probability that a randomly selected value will fall between 40 and 60.
- Problem 5: A random variable follows a Poisson distribution with a mean of 5. What is the probability that exactly 3 events occur?
- Problem 6: The waiting time between arrivals of buses at a station follows an exponential distribution with a mean of 10 minutes. What is the probability that a bus will arrive in less than 5 minutes?
Why Practice Matters

Practicing problems not only helps reinforce the theoretical concepts but also improves your speed and accuracy. Regular practice will expose you to a wide variety of problem types, helping you develop strategies to approach each one efficiently. Furthermore, reviewing the solutions after completing a problem set allows you to pinpoint mistakes and better understand the underlying principles.
By dedicating time to solving practice problems, you’ll be able to approach complex challenges with greater confidence and precision, ultimately improving your overall performance.
Understanding Conditional Probability Formulas

Conditional probability is a key concept in statistics that helps us determine the likelihood of an event occurring given that another event has already taken place. This principle is particularly useful when dealing with multiple events and can offer more accurate predictions when certain conditions are met. The following section explores the essential concepts and equations related to conditional probability and how they can be applied in practical scenarios.
Basic Concept of Conditional Probability

Conditional probability is the probability of event A occurring given that event B has already occurred. This can be mathematically expressed as:
- P(A|B): The probability of A given B. It is calculated using the formula:
P(A|B) = P(A ∩ B) / P(B)
Here, P(A ∩ B) is the probability that both events A and B occur, and P(B) is the probability of event B occurring. It is important to note that P(B) must be greater than 0 for this formula to be valid.
Examples of Conditional Probability Calculations
- Example 1: A company sells 60% red shirts and 40% blue shirts. If a customer buys a red shirt, the probability that it was made by a specific manufacturer is 0.8. What is the probability that a randomly selected shirt was both red and made by that manufacturer?
- Solution: The probability that a shirt is both red and made by that manufacturer is found by multiplying the probability of the shirt being red with the conditional probability of it being from that manufacturer:
P(Red ∩ Manufacturer) = P(Red) × P(Manufacturer|Red) = 0.60 × 0.80 = 0.48. - Example 2: In a deck of 52 cards, what is the probability of drawing a red card, given that the card drawn is a face card?
- Solution: The conditional probability is calculated as:
P(Red|Face) = P(Red ∩ Face) / P(Face) = (26/52) / (12/52) = 26/12 = 2.17.
Why Conditional Probability Matters
Conditional probability allows for more refined predictions in situations where one event is dependent on the occurrence of another. This concept is widely used in various fields such as risk management, finance, medicine, and even artificial intelligence. Mastering this technique can improve your ability to analyze and interpret data, providing deeper insights into the relationships between events.
By understanding and applying the formulas associated with conditional probability, you can approach complex problems more efficiently and make more informed decisions based on available information.
Dealing with Discrete Probability Distributions
Discrete probability distributions are a powerful tool for analyzing situations where outcomes are finite and countable. These distributions help determine the likelihood of different outcomes in scenarios like tossing a coin or rolling dice. Understanding how to calculate probabilities and interpret results is essential for analyzing random events and making informed decisions based on these probabilities.
In discrete distributions, each possible outcome has a specific probability associated with it, and the sum of all these probabilities must equal 1. Common examples of discrete distributions include the binomial distribution, Poisson distribution, and geometric distribution, each serving different types of probability scenarios.
Understanding the Probability Mass Function
The probability mass function (PMF) is used to define the probabilities of discrete random variables. Each value of the random variable has a corresponding probability, and these probabilities must add up to 1. The PMF is an essential concept in understanding how discrete probability distributions work and is widely used for calculations involving discrete variables.
| Outcome (X) | Probability (P(X)) |
|---|---|
| 0 | 0.2 |
| 1 | 0.5 |
| 2 | 0.3 |
In this table, the probabilities for each outcome sum up to 1 (0.2 + 0.5 + 0.3 = 1), confirming that this is a valid probability mass function.
Calculating Expected Value and Variance
The expected value (mean) of a discrete distribution represents the average or “long-run” value of the random variable. It is calculated by multiplying each possible outcome by its probability and summing the results. Variance measures the spread or variability of the distribution around the expected value. The formulas for calculating expected value (E[X]) and variance (Var[X]) are as follows:
- Expected Value (E[X]): E[X] = Σ (X * P(X)), where X is the outcome and P(X) is the probability.
- Variance (Var[X]): Var[X] = Σ ((X – E[X])² * P(X)), where E[X] is the expected value.
These calculations allow you to understand not only what the most likely outcomes are but also how variable the results can be.
Example: Rolling a Die
Let’s consider a simple example of rolling a fair six-sided die. The random variable X represents the outcome of the roll, which can be any of the numbers 1 through 6. Each number has an equal probability of 1/6. The probability mass function for this scenario would look like:
| Outcome (X) | Probability (P(X)) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1/6 | ||||||||
| 2 | 1/6 | ||||||||
| 3 | 1/6 | ||||||||
| 4 | 1/6 | ||||||||
| 5 | 1/6 |
| Factor | Impact on Premium |
|---|---|
| Age of Driver | Older drivers may receive lower premiums due to fewer accidents |
| Car Model | Luxury or sports cars may result in higher premiums due to higher repair costs |
| Location | High-crime areas may increase premiums due to a higher risk of theft |
By applying these techniques, professionals can ensure that their pricing reflects the true level of risk, helping to ensure profitability while maintaining competitiveness in the market.
Tips for Exam Day Success
Success on test day is not just about having the right knowledge–it’s also about preparation, strategy, and managing your mindset. Being well-prepared both mentally and physically can significantly improve your performance and help you manage the pressure of the day. Below are some practical tips that can help you approach the test with confidence and clarity.
1. Get Plenty of Rest

A good night’s sleep before the test is essential. Rest is crucial for your brain to function optimally and retain information. Aim for at least 7-8 hours of sleep to ensure that you feel refreshed and alert. Avoid staying up late to cram, as fatigue can impair your focus and decision-making during the test.
2. Arrive Early and Be Prepared
Arriving early gives you time to relax and settle in. Rushing to the testing center can increase stress and reduce focus. Make sure you have all the required materials with you, such as your identification, any allowed resources, and writing instruments. Having everything organized will help you feel calm and ready to tackle the test without unnecessary distractions.
3. Practice Time Management
During the test, it’s easy to get caught up on difficult questions. However, it’s important to pace yourself and not dwell too long on one problem. Try to estimate how much time you should spend on each section, and keep track of your progress. If a question is taking too long, move on and come back to it later. Prioritize answering all questions and then review your work if time allows.
4. Stay Calm Under Pressure
It’s natural to feel anxious on test day, but managing your nerves can make a big difference. Take deep breaths, stay focused, and keep a positive mindset. If you find yourself feeling overwhelmed, take a brief moment to close your eyes and center yourself. Staying calm helps you think more clearly and make better decisions.
5. Read Each Question Carefully
It’s easy to make mistakes by rushing through questions. Make sure to read each question carefully to understand what is being asked. Pay attention to details, such as whether the question asks for the exact value or a range. Taking the time to fully understand the question will help you avoid unnecessary errors.
By following these tips, you can set yourself up for success and approach the test with confidence, knowing that you are fully prepared to tackle any challenge that comes your way.
Common Mistakes to Avoid During the Exam
Even the most well-prepared candidates can make mistakes that affect their performance on test day. Being aware of these common errors and learning how to avoid them can make a significant difference in achieving the best possible results. Here are some mistakes to be mindful of when you’re sitting for the test.
1. Overlooking Instructions
It’s easy to jump right into answering questions, but overlooking important instructions can lead to careless mistakes. Always take a moment to carefully read the instructions at the beginning of each section and individual questions. Pay attention to specific details, such as whether the question asks for the exact value or an approximation, as this can influence how you approach solving it.
2. Mismanaging Time
Time is one of the most valuable resources during a test, and mismanaging it can lead to unnecessary stress. A common mistake is spending too much time on one question while neglecting others. It’s important to allocate time for each section and stick to it. If you encounter a challenging question, move on and come back to it later–this helps ensure that you answer all questions within the time limit.
3. Skipping Simple Questions
While it’s natural to focus on difficult questions, it’s important not to overlook the simpler ones. Skipping easy questions in favor of harder ones can waste valuable time and may cause you to miss points that could have been easily earned. Answer the straightforward questions first to build momentum and confidence, and then return to more complex problems.
4. Not Double-Checking Answers
Rushing through the test and neglecting to review your answers can lead to avoidable mistakes. After finishing each section, take a few minutes to double-check your work. This is especially important for questions that involve calculations, as simple math errors can often be caught during a quick review.
5. Not Staying Calm
Test anxiety can affect performance, leading to poor decision-making and errors. Staying calm and focused is key to avoiding mistakes. If you start to feel overwhelmed, take a few deep breaths and refocus. Managing your emotions and maintaining a calm mindset will help you think more clearly and make better decisions throughout the test.
By being mindful of these common mistakes and implementing strategies to avoid them, you can boost your confidence and improve your chances of success during the test.
Additional Resources for the Test
Preparing for a challenging assessment often requires more than just reviewing the core material. Having access to supplementary resources can help strengthen understanding, clarify difficult concepts, and provide additional practice. Here are some valuable tools and materials that can enhance your preparation and boost your confidence before the big day.
1. Textbooks and Study Guides
Comprehensive textbooks and targeted study guides are excellent resources for reviewing key concepts and problem-solving techniques. Look for books that provide both theoretical explanations and practical exercises. These guides often include step-by-step solutions and explanations that can help reinforce your knowledge and boost your problem-solving skills.
2. Online Practice Tests

One of the most effective ways to prepare for a test is through simulated practice. Online platforms that offer practice questions and full-length mock tests provide a great opportunity to experience the test environment. These resources help you familiarize yourself with the types of questions that may appear, practice pacing, and identify areas where you may need further review.
3. Forums and Study Groups
Engaging with a community of peers can be a great way to stay motivated and share resources. Online forums and study groups offer opportunities to discuss challenging problems, exchange tips, and get feedback from others who are also preparing. Collaboration can often help clarify complex topics that may be difficult to understand on your own.
4. Educational Videos
For visual learners, educational videos can be an invaluable resource. Platforms like YouTube and educational websites offer tutorials and lectures that explain key concepts and problem-solving strategies in an engaging way. Watching experts break down complex ideas can help you better understand difficult topics and retain information more effectively.
5. Flashcards and Quick Reference Guides
Using flashcards or quick-reference materials can be an efficient way to memorize key concepts and equations. These tools allow for quick review, making it easier to commit important information to memory. Consider creating your own set of flashcards based on the material you find most challenging, or use pre-made sets available online.
With these additional resources at your disposal, you can approach your preparation with more confidence and better manage any areas of difficulty, ultimately leading to a more successful performance on the day of the assessment.
How to Improve Your Recall of Key Equations
Mastering the ability to quickly recall essential equations during a test is a vital skill. To excel, it’s important not only to understand the concepts behind these equations but also to retain them in a way that makes them easy to retrieve when needed. Below are several strategies you can use to improve your memory and recall during challenging assessments.
1. Active Recall and Spaced Repetition

One of the most effective techniques for memory retention is active recall. This involves testing yourself regularly without referring to notes. The more you challenge yourself to remember key equations, the stronger the neural connections become. Pair this technique with spaced repetition, which means revisiting material at increasing intervals. This method helps move information from short-term to long-term memory, ensuring that key equations stay fresh in your mind when you need them most.
2. Visualization and Mnemonics
Visualizing equations as part of a mental image or using mnemonics can significantly improve recall. For instance, you can create a mental “picture” of an equation and associate it with a concept you’re familiar with. Mnemonics or catchy phrases that help remind you of the steps involved can also simplify complex ideas. These memory aids reduce cognitive load and make it easier to retrieve formulas when under time pressure.
3. Practice Under Time Constraints

Repetition through practice is crucial, but to simulate test conditions, it’s important to practice under time constraints. This method helps you become comfortable with recalling key equations quickly and efficiently. Set a timer and challenge yourself to solve problems while actively recalling the necessary equations without external help. Over time, you’ll improve both your speed and accuracy, allowing you to navigate challenges more easily during actual assessments.
4. Teaching Others
Explaining concepts and equations to others forces you to recall them without relying on notes. This not only strengthens your own understanding but also reinforces your memory. Try teaching friends, family, or even imaginary students about the key principles you’re studying. When you can teach it, you know you’ve truly internalized the material.
By applying these techniques, you’ll enhance your ability to recall important equations with ease, giving you the confidence to perform well and tackle any problems that arise.