The AP exam consists of a variety of questions designed to assess your understanding of key mathematical principles. The written section challenges students to demonstrate their problem-solving skills and ability to apply concepts learned throughout the course. To succeed, it is crucial to master the types of problems typically presented and understand the methodology behind crafting detailed solutions.
In this section, we will explore the critical elements of the exam’s written section from a specific year, breaking down each question and offering clear explanations. Thorough practice and preparation can significantly improve your performance and help you achieve higher marks. With detailed walkthroughs, you’ll gain insights into the most efficient techniques for approaching complex problems.
By understanding how to approach each task systematically and reviewing past solutions, you will develop a strong foundation for tackling similar questions in future exams. Emphasis will be placed on understanding core concepts, avoiding common pitfalls, and maximizing your scoring potential.
2005 AP Calculus AB Free Response Answers
The written portion of the AP exam challenges students to apply their knowledge of mathematical concepts to solve complex problems. Each question requires a clear, structured approach, where students are expected to show their reasoning and work through every step in detail. By reviewing solutions from previous years, students can better understand how to organize their responses and avoid common mistakes.
Breakdown of Key Problems
Each problem on the exam covers different aspects of the curriculum, testing both conceptual understanding and problem-solving techniques. For example, students may encounter questions that involve interpreting graphs, applying integration and differentiation methods, or solving real-world scenarios using mathematical principles. Understanding the structure of these problems helps in approaching them with the right mindset and strategies.
Effective Strategies for High Scores
To maximize your score, it’s essential to focus not only on the correct solution but also on how to present your work. Clear, logical steps, along with appropriate use of mathematical notation, play a critical role in earning full credit. Practicing with past exams and comparing your solutions to official ones is a valuable way to refine your approach and enhance your overall performance.
Overview of 2005 AP Calculus AB Exam
The AP exam tests students’ understanding and ability to apply advanced mathematical techniques in a structured format. The exam typically consists of multiple-choice questions and a written section where students must solve problems and explain their reasoning. This section is designed to assess both theoretical knowledge and practical problem-solving skills in various areas of mathematics.
| Section | Number of Questions | Time Limit | Weight |
|---|---|---|---|
| Multiple Choice | 45 | 1 hour 30 minutes | 50% |
| Written Section | 6 | 1 hour 30 minutes | 50% |
The written portion is particularly important, as it requires students to demonstrate their ability to approach complex problems systematically, showing all steps clearly. The exam focuses on key mathematical principles such as limits, derivatives, and integrals, and includes both theoretical and applied questions. Success on this portion depends on careful analysis, logical reasoning, and precise calculations.
Key Concepts in 2005 AP Calculus AB
The AP exam focuses on fundamental mathematical principles that form the basis for higher-level problem-solving and analysis. Mastery of these core concepts is essential for performing well on the test. Topics such as differentiation, integration, and the analysis of functions are central to the exam, with a heavy emphasis on applying these ideas to solve real-world problems and interpret data.
Understanding the relationship between rates of change and accumulation is key, as well as being able to work with various methods of solving differential equations and interpreting graphical representations. Another important concept is the use of limits, which forms the foundation for much of the work in the exam, especially when exploring the behavior of functions at specific points or over intervals.
Finally, proficiency in analyzing and manipulating functions, including polynomial, rational, and trigonometric types, is crucial. Strong problem-solving skills, combined with an understanding of these core topics, will allow students to effectively tackle the exam’s more complex questions.
Understanding Free Response Format
The written section of the AP exam requires students to solve complex problems and demonstrate their thought process in a clear, organized manner. Unlike multiple-choice questions, which focus on selecting the correct answer, this part tests your ability to apply concepts, reason logically, and show the steps taken to reach a solution. The format is designed to evaluate your understanding of mathematical principles in real-world contexts.
Structure of the Written Section
The written portion typically includes several questions, each requiring a detailed solution. For each problem, students must show all their work, from initial steps to the final result. Providing a step-by-step breakdown not only ensures clarity but also helps in earning partial credit, should an error occur along the way. Precision and logical flow are essential for achieving high marks.
How to Approach the Questions
When tackling these types of questions, it’s important to read each prompt carefully and identify which mathematical concepts are being tested. Strong problem-solving techniques, such as breaking down complex problems into manageable parts and checking your work, are critical for success. Additionally, be sure to use proper notation and explain your reasoning clearly. Attention to detail can significantly impact your performance in this section.
How to Approach Free Response Questions
The written section of the exam requires a strategic approach to solving problems. Unlike multiple-choice questions, where the correct answer is selected from a list, these questions demand that you clearly show your work and explain your reasoning. To excel in this section, you need to break down each problem into manageable steps, ensuring that each stage of your thought process is visible and logical.
Step-by-Step Problem Solving
One of the most effective ways to tackle these questions is by following a clear, methodical approach. Begin by reading the question carefully, identifying what is being asked, and recognizing which mathematical principles are relevant. From there, write down any formulas or equations you might need and break the problem into smaller parts.
Common Approaches to Different Problem Types
Understanding the typical structure of questions can help in preparing for them. Some questions may require you to perform calculations, while others might involve interpreting graphs or applying mathematical concepts to real-world scenarios. The following table outlines common types of problems and the approach typically used for each:
| Problem Type | Approach |
|---|---|
| Derivatives | Apply differentiation rules, simplify expressions, and interpret the result. |
| Integrals | Identify the integral setup, solve step-by-step, and interpret the meaning of the result. |
| Graph Interpretation | Analyze the graph for slopes, areas, or key points, and relate them to the question. |
| Real-World Problems | Model the situation with appropriate equations, solve, and explain your reasoning. |
Following a systematic approach, being clear in your explanations, and reviewing your work will ensure that you tackle each question with confidence and accuracy.
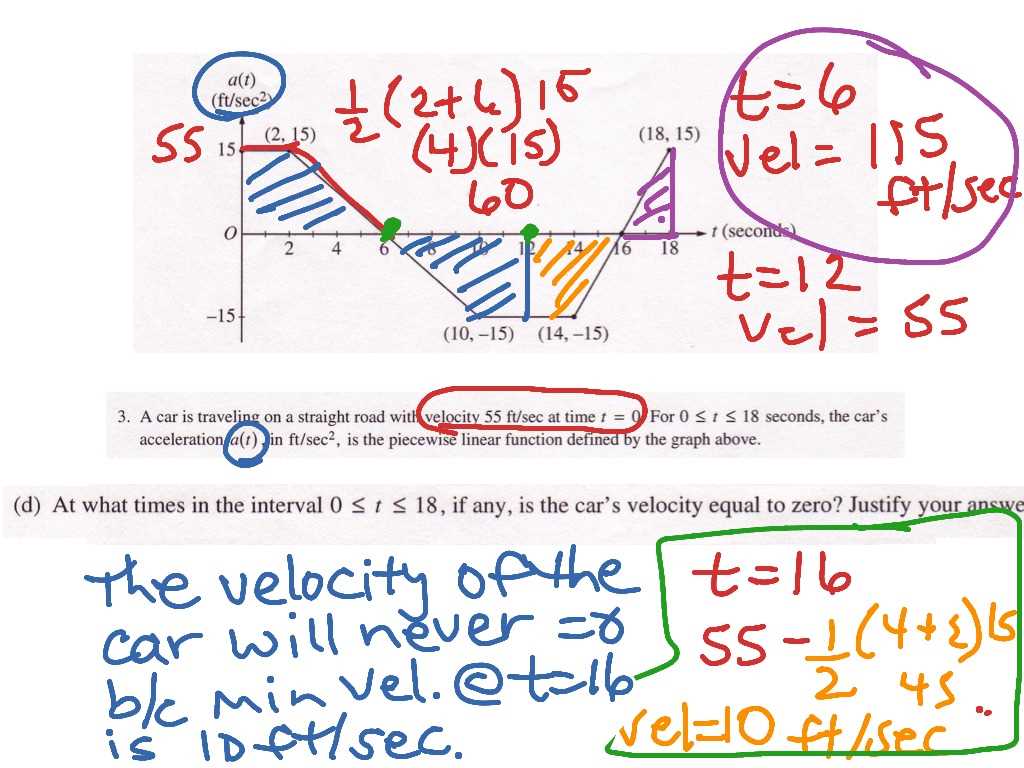
Question 1 Detailed Solution
This section provides a step-by-step breakdown of the first problem from the written portion of the exam. The problem requires a clear understanding of fundamental mathematical principles and the ability to apply them to solve a specific question. We will walk through the process, starting from interpreting the problem to obtaining the final solution.
First, let’s review the key steps needed to solve the problem:
- Identify the given information: Carefully read through the problem to understand what is provided and what is being asked. This step helps in identifying the relevant mathematical techniques to use.
- Choose the appropriate method: Based on the problem type, determine whether you need to apply a formula, work with graphs, or solve an equation. For example, this problem may involve solving for an unknown or finding a specific rate of change.
- Break down the problem: Divide the question into smaller, manageable steps. For complex problems, work through each part individually before combining the results to reach the final solution.
- Show all work clearly: Demonstrate each step of the process, ensuring that your reasoning is logical and easy to follow. This is important for earning full credit, as even if a mistake is made, partial credit may be awarded for correct methodology.
Let’s go through the solution process in detail:
- Start by using the given information to set up the problem correctly, ensuring that you are applying the right concepts.
- Next, use the relevant formulas or rules to begin solving the equation, keeping track of every step.
- If the problem involves a graph, accurately interpret the graph and use it to inform your calculations.
- Finally, check your work to ensure that all steps are logically consistent and your solution aligns with the question’s requirements.
By following these steps, you can efficiently solve the problem while ensuring clarity and accuracy in your solution.
Question 2 Answer Breakdown
This section provides a detailed analysis of the second question from the written part of the exam. The goal is to break down the solution process step by step, ensuring that every part of the problem is understood and addressed thoroughly. By examining the question in detail, you’ll be able to identify the necessary concepts and techniques needed to arrive at the correct solution.
Understanding the Problem
Start by carefully reading through the problem to identify the key components and the specific question being asked. The next steps involve choosing the right approach and applying the appropriate mathematical tools.
- Step 1: Identify the given values and the unknowns that need to be solved for.
- Step 2: Understand the type of problem you are dealing with, whether it involves optimization, related rates, or another concept.
- Step 3: Write down the equations or expressions that you will use in the solution process.
Solution Process
Now that we’ve identified the important details, we can begin solving the problem. Follow these steps for an organized and clear approach:
- Apply the appropriate formula: Depending on the problem type, apply the relevant formula, such as a differentiation or integration technique, to find an expression for the unknowns.
- Work through the math: Carry out the necessary calculations, showing each step clearly to maintain a logical flow and avoid mistakes.
- Interpret the results: Once you arrive at a solution, interpret it in the context of the problem, checking for any possible errors or misinterpretations along the way.
- Review and finalize: Ensure all parts of the question have been addressed, and verify that your solution is correct and consistent with the given information.
By following these steps, you ensure a thorough and methodical approach to solving the problem. This structure not only helps you arrive at the correct answer but also allows you to present your work clearly, which is essential in securing full credit for the written portion of the exam.
Question 3 Step-by-Step Solution
This section provides a detailed step-by-step solution to the third problem from the exam. The goal is to break down the problem into manageable steps, ensuring each aspect of the solution is thoroughly addressed. By following this process, you can better understand the necessary concepts and techniques used to reach the correct result.
Initial Analysis of the Problem
The first step is to carefully analyze the question to understand what is being asked and what information is provided. Identifying key components such as given variables, equations, and the specific task at hand will guide the solution process.
- Step 1: Read the problem thoroughly and highlight the given data and what needs to be determined.
- Step 2: Identify the relevant concepts required to solve the problem, such as functions, rates, or areas.
- Step 3: Recognize any relationships between variables that will help in solving the problem.
Solving the Problem
With the problem understood, we can now proceed to the solution. Follow these steps to break the problem into clear actions:
- Apply the necessary mathematical techniques: Depending on the type of problem, you might need to differentiate, integrate, or manipulate equations to get to the unknown value.
- Perform calculations step-by-step: Carefully calculate each part of the equation, showing all work to avoid errors and maintain clarity.
- Check the results: Once a solution is found, verify its correctness and ensure that it fits the context of the question.
- Interpret the solution: Understand what the final answer represents in relation to the question asked, and ensure it makes sense logically.
By following these steps, you can ensure a systematic and accurate approach to solving the problem, making it easier to achieve the correct answer and present your reasoning clearly.
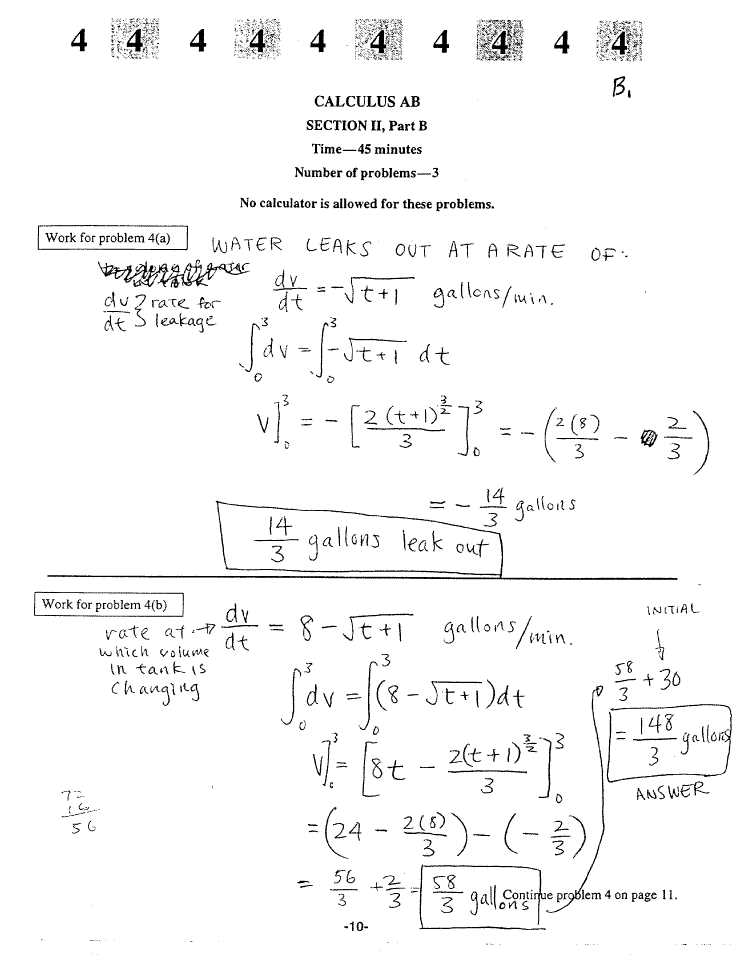
Question 4 Full Solution and Tips
This section presents a comprehensive solution to the fourth problem from the exam, along with valuable tips for approaching similar problems in the future. We will break down the solution into clear, understandable steps while providing helpful advice on how to tackle each stage of the process effectively.
Breaking Down the Problem
Before jumping into calculations, it’s important to understand the structure of the question and what it is asking. Carefully analyzing the problem is the first step in solving it efficiently. By identifying key elements and what is being asked, you can plan your approach effectively.
- Step 1: Review the problem carefully to understand the information provided and the specific goal.
- Step 2: Identify the necessary formulas or principles required to solve the problem.
- Step 3: Recognize any additional constraints or conditions that must be considered while solving.
Step-by-Step Solution
Now that we have an understanding of the problem, let’s walk through the process of solving it:
- Step 1: Set up the equation or expression based on the given data and the required task. This step will often involve using known formulas or defining variables.
- Step 2: Apply the appropriate mathematical techniques, such as differentiation, integration, or algebraic manipulation, to simplify and solve the equation.
- Step 3: Perform the necessary calculations carefully, showing each step clearly. This is important not only for accuracy but also for ensuring that your process is understandable.
- Step 4: Once you reach a solution, double-check all calculations and ensure that the results make sense in the context of the problem.
- Step 5: Interpret the results and make sure they are presented clearly and logically, ensuring that all aspects of the problem have been addressed.
Tips for Similar Problems

To improve your performance on similar problems in the future, consider the following tips:
- Tip 1: Always begin by carefully reading the problem and identifying key pieces of information.
- Tip 2: Break down the problem into smaller steps to ensure you don’t overlook important details.
- Tip 3: Show all work clearly, as it helps in organizing your thoughts and can earn partial credit if you make a mistake.
- Tip 4: Always check your final solution to ensure it makes sense and fits the context of the question.
By following these steps and applying these tips, you will be better prepared to solve similar problems with greater confidence and precision.
Question 5 Answer Explanation
This section provides a detailed explanation of the solution to the fifth question from the exam. We will go step by step through the process of solving the problem, focusing on the key concepts and techniques involved. Understanding the logic behind the steps is crucial for mastering similar types of problems in future assessments.
Understanding the Problem
Before diving into the solution, it’s essential to fully understand the problem and the specific task at hand. Identifying the given information and the goal will guide your approach, ensuring that you stay on track throughout the process.
- Step 1: Read the problem carefully and underline or highlight important data points.
- Step 2: Identify any relevant formulas or concepts needed to solve the problem, such as derivatives, integrals, or geometric properties.
- Step 3: Look for any special instructions or constraints that might influence how the solution should be approached.
Step-by-Step Solution
Once the problem is understood, we can proceed with solving it. Follow these steps for an organized approach:
- Set up the initial equation: Based on the data provided, establish the appropriate equation or expression that represents the problem.
- Apply necessary operations: Depending on the question, you might need to differentiate, integrate, or manipulate algebraic expressions to simplify the equation.
- Carry out calculations: Perform the necessary mathematical operations while showing each step clearly to avoid errors and ensure transparency in the solution process.
- Verify the result: Once you obtain a solution, review your calculations and ensure that the result aligns with the context of the question.
- Provide the final answer: Present the final solution, making sure to clearly explain what it represents in relation to the original question.
Common Pitfalls and Tips
While solving problems like this, there are a few common mistakes to watch out for, and tips to improve your approach:
- Tip 1: Pay close attention to the wording of the problem to ensure you fully understand what is being asked.
- Tip 2: Double-check your calculations at each step to catch any small mistakes early.
- Tip 3: If a problem feels complex, break it down into smaller parts and solve them sequentially.
- Tip 4: Always check your final result to ensure it makes logical sense in the context of the problem.
By following these steps and keeping these tips in mind, you can confidently approach similar problems and avoid common pitfalls, leading to more accurate and efficient problem-solving in future exams.
Important Theorems for the Exam

Mastering fundamental theorems is crucial for success in any advanced mathematical exam. These key principles form the backbone of many problems and can be applied across various topics. A solid understanding of these theorems will enable you to approach complex questions more confidently and efficiently, helping you unlock the solutions to difficult problems.
Fundamental Theorem of Analysis
This central theorem establishes the deep connection between the process of differentiation and integration. It asserts that if a function is continuous over a closed interval, then its integral can be evaluated by calculating the difference of its antiderivative at the boundaries of the interval. Understanding this principle helps simplify the evaluation of integrals and is essential for many exam problems.
Mean Value Theorem

The Mean Value Theorem explains that for any smooth curve, there exists at least one point where the rate of change of the function at that point equals the average rate of change over the entire interval. This theorem plays a significant role in proving properties of functions, solving equations, and identifying critical points, making it indispensable for exam questions.
Chain Rule
The Chain Rule is a method for differentiating composite functions. It tells us how to differentiate a function that is composed of other functions by multiplying the derivative of the outer function by the derivative of the inner function. This technique is indispensable for tackling more complicated derivatives and is commonly used in exams to handle composite expressions.
Integration by Parts
This technique is a powerful tool for solving integrals involving the product of two functions. Based on the product rule for differentiation, it allows you to break down complex integrals into simpler parts, making them easier to evaluate. Familiarity with this method is essential for solving a wide range of integral problems efficiently.
L’Hopital’s Rule
L’Hopital’s Rule is an important tool for evaluating limits that result in indeterminate forms, such as 0/0 or ∞/∞. By differentiating both the numerator and denominator, this rule allows you to simplify these limits into more manageable forms. Mastering this technique is crucial for solving limit-related problems during the exam.
Intermediate Value Theorem
The Intermediate Value Theorem states that if a function is continuous over a given interval, then for any value between the function’s values at the endpoints, there is at least one point within the interval where the function takes that value. This principle is helpful for proving the existence of solutions to equations and is often used in proofs.
Rolle’s Theorem
A special case of the Mean Value Theorem, Rolle’s Theorem asserts that if a function is continuous on a closed interval and differentiable on the open interval, with equal values at the endpoints, then there exists at least one point where the derivative of the function equals zero. This theorem is often used to find critical points or prove the existence of roots for functions.
These theorems are essential for solving a wide variety of problems on the exam. Mastering them will help you build the foundation for more advanced techniques and improve your overall problem-solving approach. By applying these key principles effectively, you’ll be well-prepared for tackling any challenge presented in the exam.
Common Mistakes to Avoid in Responses
In tackling complex mathematical problems, even the smallest mistakes can lead to significant errors. It’s important to be aware of the common pitfalls that many students fall into, as avoiding these can make a big difference in the clarity and accuracy of your solutions. By identifying and correcting these errors, you can ensure that your approach is thorough and that you maximize your potential for success.
Misunderstanding the Problem
One of the most frequent mistakes is a misinterpretation of the problem. Questions may be worded in a way that can easily lead to confusion, especially if you don’t take the time to read carefully. Always take a moment to break down the problem and highlight key details. Understanding what is being asked before you begin working through the solution will prevent unnecessary mistakes and ensure that you’re solving the right problem.
Skipping Steps or Justifying Without Explanation

Omitting intermediate steps can lead to a lack of clarity in your solution and may cause errors that are difficult to trace. Even if you think you can quickly jump to the answer, showing all steps not only helps verify the process but also demonstrates your reasoning. Furthermore, if you don’t explain how you arrived at the solution, it can be hard to track where things went wrong in case of an error.
Failing to Use Proper Notation
Mathematical notation is critical in communicating your work clearly. Inconsistent or incorrect notation can cause confusion and lead to losing points. Whether it’s using the wrong symbols, missing parentheses, or not properly indicating derivatives or integrals, maintaining correct notation is essential for making your solution understandable and demonstrating your grasp of the material. Double-check that you’re using proper mathematical conventions throughout your work.
Overlooking Units and Labels
Another common oversight is failing to include appropriate labels or units in your calculations. Units are an integral part of many mathematical problems, particularly in applied contexts. Be sure to clearly indicate the units at each stage of your work, as they are necessary for the interpretation of the answer and for the completeness of your response. Neglecting to include them can lead to misunderstandings or missed points.
Rushing Through Calculations
In an attempt to finish quickly, it’s easy to make simple arithmetic errors or skip important steps. Rushing through the process often leads to careless mistakes, such as adding numbers incorrectly or misapplying a formula. Take your time to check each step as you go. Even small errors can snowball and result in an incorrect final answer.
Ignoring Graphs and Visual Data
Some problems may provide diagrams, graphs, or tables that are integral to solving the question. Overlooking or misinterpreting these visuals can lead to errors in your approach. Make sure to carefully examine any provided visual aids, as they often contain key information that can simplify the problem or give you insights into the solution.
Neglecting to Review Your Work
Time Management During the Exam
Effective time management is a crucial skill when preparing for and completing a timed exam. It involves organizing your time wisely, ensuring you have enough for each section while also maintaining focus and clarity under pressure. A well-structured approach to time can help you avoid feeling rushed or stressed, allowing you to maximize your performance and complete all tasks thoroughly.
Start by Analyzing the Exam
Before beginning, take a few minutes to glance through the entire exam. This quick review will help you assess the difficulty of each section and the number of questions, so you can allocate time based on their complexity. Having a clear understanding of the exam’s structure will allow you to plan accordingly and stay on track throughout the test.
Efficient Pacing with Practice
Practice exams under timed conditions are a valuable way to build your pacing. By taking practice tests, you can estimate how long each type of question will take, and adjust accordingly. Understanding where you typically spend the most time can help you refine your strategy for the actual exam, ensuring that you allocate sufficient time to more challenging sections without lingering too long on easier questions.
Time Allocation Table
| Section | Time Allocation | Strategy |
|---|---|---|
| Multiple Choice | 40-45 minutes | Quickly read and eliminate incorrect answers. Don’t get stuck on difficult questions. |
| Problem-Solving | 50-60 minutes | Work through problems step by step. If stuck, move on and return to it later if possible. |
| Review Time | 10-15 minutes | Use this time to double-check answers, ensure all questions are answered, and correct any mistakes. |
Adaptability During the Exam
While planning is key, it’s important to stay adaptable. If you find yourself spending too much time on one section or question, it’s okay to shift gears and come back to it later. Being flexible allows you to move forward and ensures that you don’t fall behind schedule. Sometimes, returning to a challenging question with a fresh perspective can lead to new insights.
Use Final Moments Wisely
Once you’ve completed the exam, the remaining time should be used to review your work. Check for errors in calculations, ensure clarity in your solutions, and verify that all questions have been answered. This final review can often catch mistakes that were overlooked during the initial attempt, increasing the chances of earning extra points.
By carefully managing your time, maintaining focus, and using strategic planning, you can ensure a calm and efficient approach that will help you succeed in any timed assessment.
Scoring Criteria for Free Response Section
The evaluation process for written problem-solving sections places significant emphasis on both the accuracy of the final solution and the clarity of the methodology used to arrive at it. Scorers assess not just the correct answer but the logical steps taken to solve the problem, the application of relevant concepts, and the presentation of work in an organized manner. Understanding the grading criteria is essential for maximizing points during these sections of the examination.
Key Factors in Scoring
Examiners evaluate the work based on specific aspects that demonstrate the student’s understanding and problem-solving skills. A correct solution, explained step-by-step with appropriate justification, holds the highest value. Below is an outline of the major components considered during grading.
Scoring Breakdown
| Criterion | Points | Description |
|---|---|---|
| Accuracy of Final Answer | 2-4 points | The final result must be correct. Partial credit may be awarded for correct processes, even if the final answer is wrong. |
| Logical Process and Method | 3-5 points | The approach should be logically sound and follow a structured procedure. Correct use of formulas and theorems should be demonstrated. |
| Clarity and Organization | 1-2 points | Answers should be clearly written, with each step presented in an orderly manner. The work should be easy to follow and well-structured. |
| Correct Application of Mathematical Concepts | 2-3 points | The student must apply the correct concepts, formulas, or principles at every step of the solution. Any misapplication or omission of key concepts will lead to deductions. |
| Explanation and Justification | 1-2 points | Each step in the process should be explained or justified. Providing reasoning for the chosen methods adds to the overall score. |
Additional Points to Consider
While scoring heavily relies on the final answer, partial credit is often awarded for showing a deep understanding of the problem-solving process. If the logical steps are correct but a minor error is made in calculations, credit is typically given for the demonstrated process. The key to securing the highest possible score is not only providing the correct final result but also showing a structured and logical approach to reach that result.
By aligning your approach with the outlined criteria–emphasizing accuracy, clarity, logical processes, and justified reasoning–you can significantly improve your performance in the written sections of the examination. A well-organized and thoroughly explained solution is more likely to earn full credit, even if there are minor computational errors.
How to Earn Full Credit on Free Response
Achieving the maximum score on written problem-solving sections requires more than just finding the right solution. It involves demonstrating a deep understanding of the material and showcasing the ability to apply concepts in a clear, logical, and structured way. To ensure you earn full credit, it’s crucial to approach each question methodically and follow key strategies throughout your work.
Key Strategies for Maximizing Points
- Show Your Work: Always display each step of your solution. Even if you reach the correct final answer, omitting intermediate steps may result in losing valuable points. Provide clear reasoning for each step to ensure examiners understand your thought process.
- Organize Your Work Clearly: Neatness and structure are critical. Write your solutions in a logical sequence, clearly separating each part of the problem. Use labels, bullet points, or numbers if necessary to differentiate between steps.
- Use Proper Notation: Be precise with mathematical symbols and terminology. Incorrect or inconsistent notation can confuse graders and result in point deductions.
- Check for Mathematical Consistency: Make sure your methods align with the principles of the subject. Avoid skipping steps or using shortcuts without justification. Properly applying relevant formulas, rules, and theorems is crucial for earning full credit.
How to Address Specific Problem Types
- For Derivative or Integral Questions: Always begin by stating the formula or rule you’re using, then show how it’s applied step by step. If required, verify your answer by considering different methods or discussing the implications of your result.
- For Word Problems: Take time to identify the key information and translate it into a mathematical model. Define all variables and explain the relationships between them. Be sure to present a clear solution, highlighting both the methodology and final outcome.
- For Graphical Questions: Clearly label the graph and indicate any critical points or regions. Make sure to explain how you arrived at these conclusions and provide any necessary calculations to back up your interpretations.
By focusing on clarity, structure, and a well-organized approach, you can demonstrate your full understanding and achieve full credit on written problem-solving sections. Always remember to explain your reasoning and avoid shortcuts unless they are thoroughly justified. The goal is not just to provide the correct answer, but to make the grader’s job easier by presenting a well-documented, logical solution.
Practice Tips for AP Calculus Success

Achieving success in advanced mathematics exams requires more than just passive studying. To truly master the material, students need to engage in consistent practice, refine their problem-solving techniques, and develop a strategic approach to tackling exam questions. The key is to focus on both understanding concepts and honing the skills necessary to apply them effectively under timed conditions.
Effective Practice Strategies
- Understand Core Concepts: Before diving into practice problems, make sure you fully grasp the fundamental concepts. Understanding the “why” behind formulas and methods is crucial for solving complex problems effectively.
- Work Through Practice Problems: Consistent practice is essential. Solve a wide variety of problems, especially those that challenge you. Focus on both conceptual questions and those requiring detailed calculations.
- Time Yourself: Simulate exam conditions by timing your practice sessions. This will help you manage your time more effectively during the actual exam and get used to working under pressure.
- Review Mistakes: After completing each practice set, carefully review your mistakes. Understand where you went wrong and focus on improving those areas. Revising errors helps reinforce your understanding and prevents repeating the same mistakes.
Additional Tips for Maximizing Performance
- Use Multiple Resources: Don’t limit yourself to just one textbook or set of notes. Explore different resources such as online tutorials, study guides, and practice exams. A diverse range of practice will help you encounter problems from different angles.
- Seek Help When Needed: If you’re struggling with certain concepts, don’t hesitate to ask your teacher or peers for clarification. Sometimes, a different explanation or approach can make all the difference in understanding a topic.
- Master Key Formulas: Certain formulas are fundamental to solving problems efficiently. Memorize essential formulas, but also understand their derivations and applications. This deeper understanding will help you use them correctly in various situations.
- Focus on Problem-Solving Strategies: Develop a systematic approach to problem-solving. Break down each problem into manageable steps, and always double-check your work for accuracy.
By implementing these strategies, you’ll be well-prepared for tackling any question that comes your way. Consistent practice, a solid understanding of core principles, and a strategic approach to exam preparation will give you the best chance of succeeding in advanced mathematics assessments.
Resources for Further AP Study
Enhancing your understanding and performance in advanced mathematics requires a variety of study materials and strategies. The key to mastering complex concepts and excelling in exams is to utilize diverse resources that cater to different learning styles. Whether you’re looking for textbooks, online platforms, or practice tests, each resource offers unique ways to reinforce your knowledge and sharpen your skills.
Textbooks and Study Guides
Comprehensive study guides provide a structured approach to reviewing key topics. These books often include in-depth explanations, example problems, and practice exercises to test your understanding. A few well-known options include:
- Gruber’s Complete SAT Guide – A trusted resource that covers a wide range of advanced topics.
- CliffsNotes AP Mathematics – A condensed guide that highlights essential formulas and concepts.
- AP Review Books – Books published specifically for exam prep, which contain practice questions and detailed solutions.
Online Platforms and Tools
For interactive learning and additional practice, many online resources can supplement your study routine:
- Khan Academy – A free platform offering video lessons on various mathematical topics, from basic principles to more advanced techniques.
- PatrickJMT – Provides clear and concise video tutorials, focusing on solving specific problems step by step.
- Brilliant.org – Offers problem-solving exercises and in-depth lessons to foster critical thinking and application of mathematical concepts.
Additionally, practice tests and past exam questions are valuable tools for familiarizing yourself with the format and types of questions you may encounter on the actual assessment.
Discussion Forums and Peer Support
Online forums and study groups can be excellent resources for discussing tricky topics and gaining new perspectives. Platforms such as:
- Reddit’s AP Math Subreddit – A community where students share tips, resources, and solutions to common challenges.
- College Confidential – Offers discussions around exam preparation and strategies, with feedback from other students and educators.
Working together with peers can deepen your understanding of difficult concepts and provide motivation through collaboration.
By utilizing a variety of these tools and resources, you’ll be better equipped to tackle the challenges of advanced mathematics and achieve the success you’re aiming for.
How This Exam Prepares You for College
Taking a challenging assessment in advanced mathematics equips students with essential skills that will serve them well in higher education. Beyond testing knowledge, this examination encourages critical thinking, problem-solving, and the ability to apply theoretical concepts to practical situations. These are the very skills that college courses demand, especially in subjects requiring analytical reasoning and quantitative analysis.
Time Management and Focus – One of the most important aspects of this exam is its ability to help students improve their time management skills. In college, students are often faced with multiple assignments and deadlines. This exam trains you to prioritize tasks, allocate time efficiently, and maintain focus under pressure, skills that are essential for success in any academic field.
Problem-Solving Abilities – The exam emphasizes solving complex problems by breaking them down into manageable steps. This mirrors the type of work you will encounter in higher education, where problems may not always have straightforward solutions. Learning to analyze problems from multiple angles and using logical reasoning to find answers is a valuable skill in all college disciplines, from engineering to economics to the sciences.
Preparation for Advanced Topics – Many college courses build upon the foundational knowledge tested in this exam. The concepts explored provide a strong base for further study in mathematics, economics, physics, and other fields. By mastering these topics, you will have a head start in university courses that build on similar principles.
In summary, while this exam may seem daunting, it is ultimately an investment in your academic future. The skills and knowledge you gain will help you thrive not only in the exam but in your college education and beyond.