
Preparing for an important math assessment can be daunting, but understanding the process and mastering key techniques can make all the difference. This section provides a detailed guide to solving problems, showcasing not just the final results but also the logical steps taken to reach them. By breaking down complex questions into manageable steps, you’ll gain confidence and clarity.
Each solution here offers insight into the methods used to approach common problems, with a focus on clarity and thoroughness. Whether you’re reviewing algebraic expressions, geometric principles, or advanced calculations, these step-by-step guides will support your learning and exam readiness. Remember, it’s not just about getting the right result–it’s about understanding how to get there.
Mastering these techniques will not only help you succeed on the test but also strengthen your overall mathematical skills. By practicing these methods and analyzing the solutions, you will be better equipped to handle any question that comes your way.
June 2025 Geometry Regents Answers with Work
In this section, we explore the solutions to common mathematical problems presented during the exam. Each problem is broken down into its key components, demonstrating the processes involved to arrive at the correct solution. By examining the steps involved, students can better understand how to approach similar questions in future assessments.
Problem Breakdown and Detailed Steps
Understanding the logical sequence behind each solution is crucial for mastering the content. The problems are solved step by step, ensuring clarity at every stage of the process. Here’s an example breakdown:
- Identify the given information and what is being asked.
- Choose the appropriate formula or method for solving the problem.
- Work through the calculations, showing every step for accuracy.
- Double-check the final result and ensure it makes sense in the context of the problem.
Key Techniques and Tips for Success
In addition to problem-solving steps, it’s important to familiarize yourself with the methods and strategies that can improve efficiency and accuracy during the exam:
- Practice common patterns of questions to identify them more quickly.
- Focus on understanding the logic behind the calculations, not just memorizing formulas.
- Always verify your final answers, especially for complex problems.
- Review key concepts regularly to maintain a strong grasp of the material.
By practicing these techniques, you’ll be better prepared for any problem that comes your way, ensuring you approach each question with confidence and clarity.
Overview of June 2025 Geometry Exam
This section provides a comprehensive overview of the upcoming math evaluation, highlighting its structure, key components, and what to expect on exam day. Understanding the layout of the assessment and the types of questions will help you prepare effectively and ensure you are ready for every aspect of the test.
Structure and Format
The exam is designed to test your knowledge across several mathematical areas, focusing on logical reasoning, spatial understanding, and problem-solving skills. It consists of multiple sections, each targeting a different set of skills. Typically, you can expect:
- Multiple-choice questions to assess foundational concepts.
- Short-answer questions that require clear, step-by-step solutions.
- Longer, more complex problems that demand a deeper understanding of principles.
What to Expect on Test Day
On the day of the exam, it’s essential to be prepared both mentally and physically. Focus on the following:
- Ensure you have all necessary materials, such as a calculator, pencils, and an eraser.
- Read each question carefully and allocate your time wisely.
- Stay calm and confident; rely on your preparation and techniques to guide you.
By understanding the structure and preparing effectively, you’ll be in a stronger position to succeed and perform well on the test.
Step-by-Step Solutions for Each Problem
This section provides detailed, step-by-step guidance for solving mathematical challenges. Breaking down each problem into manageable steps allows for a clearer understanding of the methods and techniques used to reach the correct result. By following the outlined procedures, you’ll gain insights into how to approach similar problems effectively.
Problem 1: Solving Linear Equations
Start by identifying the equation and isolating the variable. Here’s how you can approach it:
- Examine both sides of the equation and simplify if needed.
- Move terms involving the variable to one side by adding or subtracting.
- Apply inverse operations (multiplication or division) to isolate the variable.
- Check your solution by substituting the value back into the original equation.
Problem 2: Working with Angles and Triangles
For problems involving angles, particularly in triangles, follow these steps:
- Identify known angles and apply geometric properties like the sum of angles in a triangle.
- Use the Pythagorean theorem or trigonometric ratios when applicable.
- Label all sides and angles clearly, using the correct units of measurement.
- Verify the final result using relevant theorems or properties of the triangle.
By mastering these approaches, you can tackle a variety of problems, gaining confidence in your mathematical reasoning and problem-solving skills.
How to Approach Geometry Regents Questions
Approaching mathematical problems effectively requires understanding the underlying concepts and applying the correct strategies. Whether dealing with algebraic expressions, spatial reasoning, or applying theorems, it’s essential to stay focused and organized when solving each problem. This section outlines proven techniques for tackling questions methodically to ensure accuracy and efficiency.
Step-by-Step Process for Solving Problems
Breaking down each question into smaller, more manageable steps allows for a systematic approach to solving the problem. Follow these general guidelines:
| Step | Action |
|---|---|
| 1 | Read the question carefully to identify the given information and what is being asked. |
| 2 | Sketch diagrams or figures where necessary to visualize the problem. |
| 3 | Determine the most relevant formulas or principles for solving the problem. |
| 4 | Apply the formulas step by step, ensuring every calculation is shown clearly. |
| 5 | Review the solution to ensure it answers the question correctly and make adjustments if needed. |
Strategies for Managing Time and Accuracy
Time management is crucial during the exam. By applying efficient problem-solving strategies, you can balance speed and precision. Consider the following tips:
- Prioritize easier questions first to build confidence and gain time for more complex ones.
- Check your work as you go to minimize careless mistakes.
- If stuck on a problem, move on and come back to it later with a fresh perspective.
By following these techniques, you can tackle questions more effectively, ensuring you approach each challenge with confidence and clarity.
Key Formulas for Geometry Regents Exam

Mastering key mathematical formulas is essential for solving problems quickly and accurately. These formulas serve as the foundation for many questions and help simplify complex calculations. Understanding when and how to use them can significantly improve performance on the exam.
Essential Formulas for Success
Below is a list of the most important formulas that will help you navigate through a variety of questions:
- Area of a Triangle: ( A = frac{1}{2} times text{base} times text{height} )
- Area of a Rectangle: ( A = text{length} times text{width} )
- Pythagorean Theorem: ( a^2 + b^2 = c^2 ) (for right triangles)
- Circumference of a Circle: ( C = 2 pi r )
- Area of a Circle: ( A = pi r^2 )
- Volume of a Rectangular Prism: ( V = text{length} times text{width} times text{height} )
- Volume of a Cylinder: ( V = pi r^2 h )
Additional Key Concepts to Remember
In addition to the fundamental formulas, it is important to understand the application of various principles and properties:
- Sum of Angles in a Triangle: ( 180^circ )
- Sum of Angles in a Quadrilateral: ( 360^circ )
- Similar Triangles: Corresponding angles are equal, and the sides are proportional.
- Area of a Sector: ( A = frac{theta}{360^circ} times pi r^2 ), where ( theta ) is the central angle in degrees.
By memorizing these formulas and understanding how to apply them, you will be well-equipped to solve a wide range of problems effectively.
Detailed Work for June 2025 Answers

This section provides a thorough breakdown of each solution, showcasing the step-by-step process required to reach the correct result. By examining the methods used to solve various problems, you can gain a deeper understanding of how to apply mathematical principles and techniques effectively. The goal is to ensure clarity and accuracy at each stage of the problem-solving process.
Step-by-Step Explanation of Common Problems

Each problem is addressed in a structured manner to ensure all aspects of the solution are clear. Below is an example of how to solve a typical question:
- Identify and define the known values, such as angles, sides, or other relevant measurements.
- Determine the appropriate formula or theorem to apply based on the given information.
- Execute the calculations carefully, showing all intermediate steps to avoid errors.
- Review the result to ensure it fits within the context of the problem and double-check calculations for accuracy.
Application of Key Theorems and Formulas
In addition to the steps above, applying the right mathematical concepts is essential to solving each problem efficiently. For example, the Pythagorean Theorem can be used for right triangles, while properties of similar triangles help in proportional reasoning. Ensuring you know when and how to apply each formula will save valuable time and reduce the risk of mistakes.
By following this detailed approach, you will not only arrive at the correct solutions but also strengthen your understanding of the concepts needed to tackle a wide range of questions on the test.
Understanding the Geometry Regents Format
Knowing the layout of the test is crucial to performing well. Familiarity with the structure helps manage time effectively, avoid surprises, and ensure each section is tackled systematically. This section explains the typical format of the exam, highlighting the types of questions you can expect and how to prepare for them.
Test Breakdown and Question Types
The examination is divided into multiple sections, each designed to assess different areas of mathematical understanding. Understanding the distribution of questions across these sections is key to managing your time and effort.
| Section | Description | Question Types |
|---|---|---|
| Section 1 | Multiple-choice questions that test basic concepts and understanding. | 4-6 options, only one correct answer per question. |
| Section 2 | Short-answer questions where you must show your steps and arrive at the final solution. | Direct problem-solving with intermediate steps required. |
| Section 3 | Longer, more complex problems that often combine several concepts. | Step-by-step solutions, requiring detailed explanation and justification. |
How to Approach Each Section

Each section has a specific approach to maximize efficiency and accuracy:
- For multiple-choice: Read all options carefully and eliminate clearly incorrect answers first. This increases your chances of selecting the right one.
- For short-answer questions: Show all work, even if it seems simple, to ensure full credit for each step.
- For long problems: Break down the question into smaller parts, solve each part step-by-step, and double-check your final result.
By understanding the exam format, you can allocate time effectively and approach each section with confidence, maximizing your performance on test day.
Common Geometry Mistakes to Avoid
When solving mathematical problems, it’s easy to overlook small details or make assumptions that lead to incorrect results. Recognizing and avoiding common errors can greatly improve accuracy and efficiency in problem-solving. This section highlights some frequent mistakes and offers tips on how to avoid them.
Common Errors and How to Prevent Them
- Misapplying Formulas: Using the wrong formula or misapplying a formula is a common mistake. Always double-check which formula is appropriate for the specific problem at hand.
- Skipping Units: Failing to keep track of units or converting them incorrectly can lead to mistakes in your final answer. Always ensure units are consistent throughout the calculations.
- Forgetting to Simplify: Sometimes, calculations are left in a complicated form without being simplified. Ensure you simplify expressions fully before finalizing your answer.
- Ignoring Key Information: Failing to note all the given information or assumptions can cause incorrect results. Take time to carefully read through each problem and highlight important data.
- Misinterpreting Diagrams: Diagrams are crucial in many problems, and ignoring them or misinterpreting their details can lead to wrong answers. Always analyze the diagram before proceeding.
Tips for Avoiding These Errors
- Double-check work: Go over each step in your solution to ensure accuracy and consistency.
- Use logical reasoning: Carefully consider the context of the problem and whether the solution makes sense.
- Practice regularly: The more problems you solve, the more familiar you become with common pitfalls, which helps avoid repeating mistakes.
By recognizing these common mistakes and taking the time to avoid them, you can enhance your problem-solving skills and improve your chances of success on the test.
Effective Study Strategies for Geometry Regents
Preparing for a mathematics exam requires more than just reviewing notes; it involves a focused approach to mastering key concepts and solving problems efficiently. Effective study strategies can help you retain crucial information, develop problem-solving skills, and manage your time on exam day. This section outlines practical methods to enhance your preparation and improve your performance.
Focus on Core Concepts
Understanding the foundational principles is essential for success. Begin by reviewing the key topics and ensure you grasp the basic concepts. Instead of memorizing formulas, aim to understand how and when to apply them. This will allow you to solve problems with confidence and avoid unnecessary mistakes.
Practice Regularly
One of the most effective ways to prepare is by practicing problems consistently. Start with simpler questions to build your confidence, then gradually work up to more challenging ones. This not only reinforces your understanding but also helps you get accustomed to the format of the questions. The more problems you solve, the more comfortable you’ll become with the material.
Use Study Guides and Resources
Take advantage of available study materials such as textbooks, online resources, and practice exams. Study guides often provide summaries of important concepts, along with sample questions that mimic those on the test. Reviewing past exams can give you insight into the types of problems you may encounter and help you identify areas that need improvement.
Join Study Groups
Collaborating with others can be a valuable way to reinforce learning. Join a study group or find a study partner to discuss difficult problems, share strategies, and provide feedback. Teaching others what you’ve learned is also a great way to solidify your understanding of key concepts.
Time Management and Breaks
Effective study isn’t just about how much time you spend, but how you manage it. Break your study sessions into focused intervals, with short breaks in between. This technique, known as the Pomodoro method, helps maintain concentration and prevents burnout. It’s important to stay fresh and avoid overloading yourself with information.
By adopting these study strategies and maintaining a consistent, focused effort, you will be better prepared for the exam and feel more confident in your ability to solve problems efficiently.
Tips for Managing Time During the Exam
Effective time management during an exam is essential for maximizing performance. With multiple questions to answer, it’s important to allocate your time wisely and avoid getting stuck on difficult problems. This section offers strategies to help you stay on track and complete the exam within the allotted time.
Prioritize and Plan
Before you start answering questions, quickly skim through the entire test to get a sense of the question types and their difficulty. Prioritize the questions that seem easier or require less time to solve. It’s better to tackle simpler problems first, ensuring that you accumulate points early in the exam. This way, you can leave more time for the challenging ones later on.
Time Allocation per Section

Set a time limit for each section based on its length and complexity. For example, if a section has 10 questions, you can allocate around 1-2 minutes per question, depending on the difficulty. If you find yourself spending too much time on a single question, move on and return to it later if time allows. This will prevent you from wasting valuable time on a single problem.
Avoid Perfectionism
While it’s important to provide accurate answers, striving for perfection can sometimes lead to wasted time. If you feel uncertain about a question, give your best effort and move on. You can always come back to it later. Spending too much time on one problem can jeopardize your ability to answer other questions, reducing your overall score.
Use the Process of Elimination
If you’re unsure of an answer, use the process of elimination to narrow down the choices. This can help you make an educated guess, saving time instead of trying to figure out the perfect solution for every question.
By implementing these time management techniques, you can ensure that you approach the exam in an organized and strategic way, helping you to finish within the time limit and maximize your potential score.
Practice Problems with Detailed Solutions
Practicing problems and reviewing step-by-step solutions is a powerful way to solidify understanding and improve problem-solving skills. In this section, we provide a selection of problems designed to test various concepts, along with comprehensive solutions to guide you through the process. By working through these examples, you can gain a deeper understanding of the material and refine your approach to different types of questions.
Example 1: Solving for Area
Consider the following problem:
- A rectangle has a length of 10 units and a width of 4 units. What is its area?
Solution:
- The formula for the area of a rectangle is: Area = length × width.
- Substitute the given values: Area = 10 × 4 = 40.
- The area of the rectangle is 40 square units.
Example 2: Solving for Angles
Now, let’s look at a problem involving angles:
- In a triangle, one angle measures 40°, and another measures 75°. What is the measure of the third angle?
Solution:
- The sum of the angles in a triangle is always 180°.
- To find the third angle, subtract the sum of the given angles from 180°: 180° – (40° + 75°) = 180° – 115° = 65°.
- The third angle measures 65°.
Example 3: Solving for Perimeter
Here’s a problem that involves finding the perimeter:
- A square has sides of length 6 units. What is its perimeter?
Solution:
- The formula for the perimeter of a square is: Perimeter = 4 × side length.
- Substitute the given value: Perimeter = 4 × 6 = 24.
- The perimeter of the square is 24 units.
Working through practice problems like these is crucial for reinforcing your skills. Be sure to understand each step and take the time to solve similar problems to ensure you’re prepared for the exam.
How to Interpret Regents Geometry Questions
Understanding the phrasing of test questions is essential for successfully navigating any exam. Often, questions may include specific instructions or use terminology that can be tricky if you’re not familiar with how it’s presented. This section will guide you through strategies for interpreting questions accurately, so you can approach each one with confidence and avoid common pitfalls.
Carefully Read Each Question
The first step in interpreting any question is to read it thoroughly. Many students rush through the text and miss key details. Take your time to ensure you understand what is being asked. Pay attention to:
- Important keywords such as “find,” “calculate,” or “determine.”
- Specific conditions or constraints mentioned in the question.
- Any visual aids like diagrams or graphs that accompany the question.
Identify Key Information
Once you’ve read the question, identify the important pieces of information that are necessary to solve it. Highlight or underline numbers, shapes, and any other relevant details. Some questions may contain extra information that is not needed, so be careful not to get distracted by irrelevant details.
Understand What the Question is Asking
After identifying the key information, determine exactly what the question is asking. Is it asking you to calculate a measurement, explain a concept, or solve for a variable? Knowing this will guide your approach and ensure you’re solving for the correct element.
Break Down Complex Questions
If a question is complex or involves multiple parts, break it down into smaller steps. Work through each part methodically. For example:
- Start by identifying the given information.
- Look for relationships or formulas that can be applied.
- After applying each formula or method, check the results at each step.
By taking a systematic approach to interpreting questions, you’ll be able to avoid confusion and ensure that you’re solving the problem correctly. This clarity will also help manage your time effectively during the exam.
Review of Essential Geometry Concepts
Mastering foundational principles is crucial for success in any math-based exam. A strong understanding of key concepts enables you to approach complex problems with confidence and clarity. This section revisits the core topics that form the basis of many questions, ensuring that you’re well-prepared to tackle various problems effectively.
Basic Shapes and Properties
The study of shapes is central to this field. From simple polygons to more complex figures, knowing their properties is fundamental. Be sure to recall the characteristics of common shapes such as:
- Triangles (equilateral, isosceles, scalene)
- Quadrilaterals (squares, rectangles, trapezoids)
- Circles (radius, diameter, circumference)
Each shape has its own set of rules, including angles, sides, and symmetry. Understanding these characteristics allows for solving problems related to area, perimeter, and other measurements.
Angle Relationships
Angles play a significant role in geometry, and recognizing various angle relationships is vital. Key relationships include:
- Complementary and supplementary angles
- Vertical angles
- Alternate interior and exterior angles
These relationships are frequently tested in problems that require you to find unknown angles or use them to solve for other unknowns.
Area and Volume Formulas
Knowing how to calculate the area and volume of various shapes is an essential skill. Review the formulas for:
- Area of triangles, rectangles, and circles
- Surface area and volume of cubes, spheres, and cylinders
- Prisms and pyramids
These calculations often appear in multiple-choice or open-ended questions. Practice applying these formulas quickly and accurately to save time during the exam.
Coordinate Geometry
Coordinate geometry connects algebraic equations with geometric shapes. Review how to use the coordinate plane to find:
- The distance between two points
- The midpoint of a line segment
- The slope of a line
These concepts are crucial when working with problems involving lines, slopes, and graphs.
Congruence and Similarity
Another important concept is the relationship between shapes that are congruent (identical in shape and size) or similar (same shape, but possibly different sizes). Understanding how to use transformations, dilations, and proportions will help you solve problems that require proving triangles or other figures are congruent or similar.
By reviewing these core concepts, you’ll strengthen your foundation and increase your ability to solve problems confidently and efficiently. Familiarity with these principles is key to succeeding in exams that test your understanding of spatial relationships and mathematical reasoning.
How to Check Your Geometry Work
Verifying your solutions is an essential part of any mathematical task. Ensuring that each step is accurate can prevent mistakes from affecting your final answer. This process involves re-evaluating your calculations, checking logical steps, and confirming that your results make sense in the context of the problem. Below are several methods to help you check your work thoroughly.
Revisit the Problem Statement
Before you finalize any solution, read the problem again. Make sure you understand all the given information and what the question is asking. Sometimes, the answer lies in revisiting the problem and checking if you’ve missed any key details or misunderstood the requirements.
Double-Check Calculations
Carefully review your calculations for potential arithmetic errors. For example, when finding areas, perimeters, or angles, go over your mathematical operations step by step. A simple mistake, such as misplacing a decimal point or forgetting a sign, can lead to incorrect results.
Use Different Methods
Whenever possible, try solving the problem using an alternative method. For example, if you used a formula to calculate the area of a shape, check the result by measuring the dimensions directly (if applicable) or applying a different formula that gives the same result. Comparing results from different approaches can help ensure accuracy.
Verify Units and Dimensions
Ensure that all units are consistent throughout your solution. If the problem involves distances or areas, check that you’re using the correct units for each step. For example, if the answer is supposed to be in square units, ensure that all side lengths were squared correctly. Also, make sure that you haven’t mixed up different units, like inches and centimeters.
Look for Common Mistakes
Some mistakes are more common than others in spatial problems. Watch out for:
- Forgetting to apply the correct formula
- Confusing the properties of similar and congruent shapes
- Misinterpreting the symmetry of a figure
- Incorrectly applying angle relationships
By anticipating these common pitfalls, you can be more alert and avoid them during your review.
Confirm the Final Answer Makes Sense
Once you’ve completed your solution, take a step back and ask yourself whether the result seems reasonable. Does the answer fit the context of the problem? If something seems off, it’s worth rechecking your steps to ensure everything adds up logically. The final answer should align with your expectations based on the problem’s conditions.
By following these steps and taking the time to review your work carefully, you can reduce errors and increase your confidence in your results. Verification is an important skill in mathematics, and developing the habit of double-checking can improve both accuracy and efficiency.
How to Use Answer Keys for Studying
Answer keys can be a powerful tool for reinforcing understanding and improving problem-solving skills. By carefully analyzing the provided solutions, students can identify areas of weakness and develop a deeper understanding of the material. However, it’s important to use answer keys in a thoughtful and strategic way to maximize their effectiveness.
Understand the Solution Process
Rather than simply comparing your results to the provided answers, take the time to study the steps involved in reaching the solution. Break down each step and try to understand why it was performed that way. This will help you grasp the underlying principles and improve your ability to tackle similar problems independently in the future.
Identify Mistakes and Learn from Them
If your solution differs from the one in the answer key, don’t just accept it as a mistake. Go through the problem again and compare your method to the correct steps. Understanding where you went wrong is a crucial part of learning. Whether it’s a calculation error, a misunderstanding of a concept, or a misapplication of a formula, addressing these mistakes will help prevent them in the future.
Practice with Variations
Once you’ve reviewed the solution and understood the correct approach, try working through similar problems. Modify the figures or values slightly and solve the problems again. This will reinforce your learning and allow you to apply the same techniques to different scenarios, enhancing your problem-solving versatility.
Focus on Key Concepts
Answer keys often highlight important concepts or strategies that are central to solving problems. Use these as a guide to focus your study sessions on understanding these core principles. Review any concepts that appear frequently in the solution process and ensure you have a solid grasp of them.
Use Answer Keys as a Supplement, Not a Crutch
While answer keys are helpful, they should not be relied upon too heavily. Aim to solve the problems on your own first, and use the key as a reference only when necessary. Over-reliance on answer keys can hinder your ability to think critically and solve problems without external help.
By strategically using answer keys in your study routine, you can reinforce your understanding, identify areas of improvement, and ultimately increase your ability to succeed in future problem-solving tasks.
Review of Key Geometric Figures and Properties
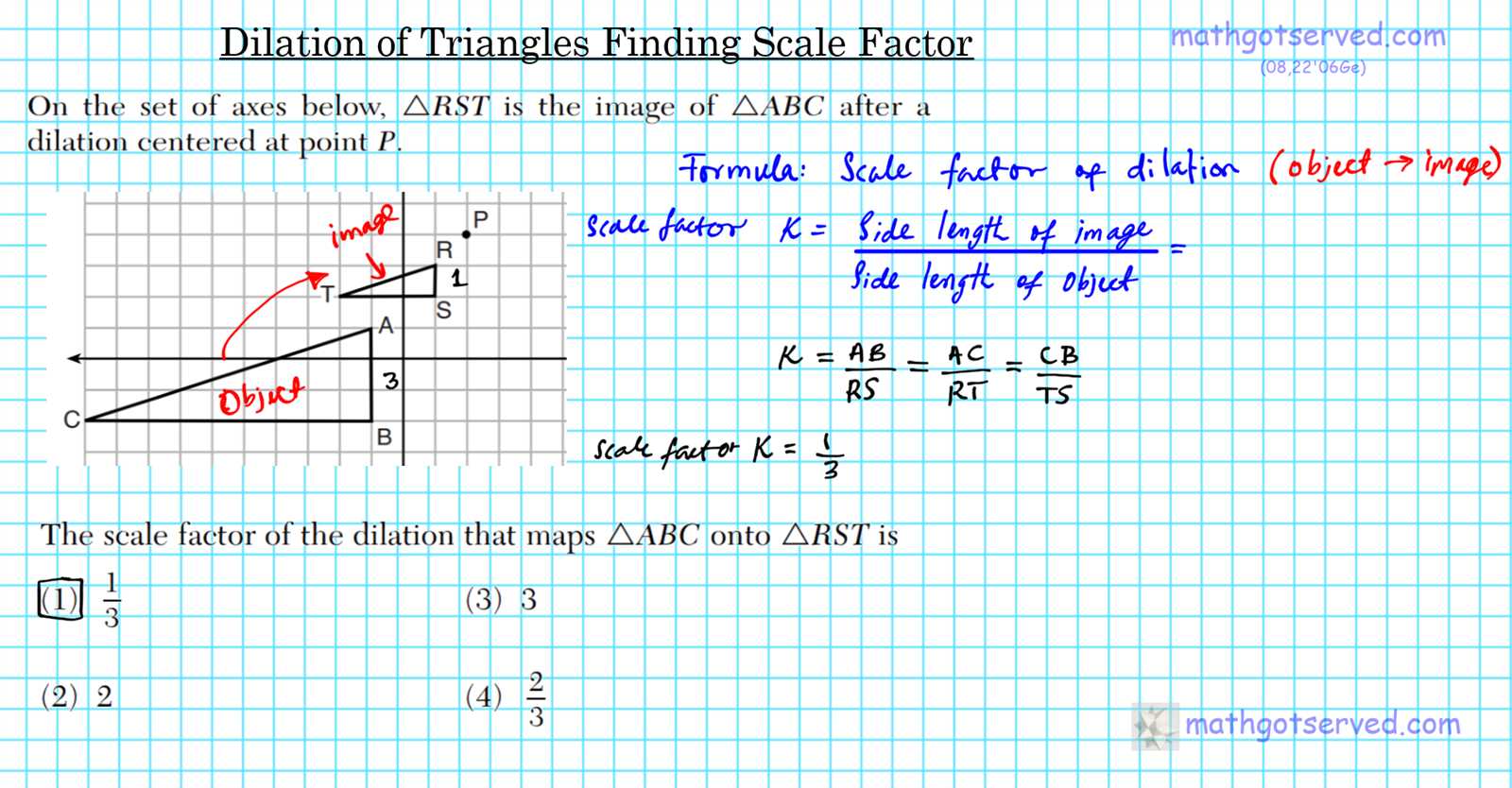
Understanding the fundamental shapes and their characteristics is essential for solving related problems efficiently. This section will cover the primary figures commonly encountered in problem sets, focusing on their properties, formulas, and how they are interrelated. A solid grasp of these shapes and their attributes can significantly improve problem-solving ability.
Triangles
Triangles are one of the most basic yet essential figures in mathematics. They come in different types, including equilateral, isosceles, and scalene, each with distinct properties. The sum of the interior angles of any triangle is always 180°. Additionally, the Pythagorean Theorem is critical for right triangles, helping determine the length of the sides.
Properties of Triangles
| Type of Triangle | Properties |
|---|---|
| Equilateral | All sides and angles are equal (each angle is 60°). |
| Isosceles | Two sides are equal, and the angles opposite these sides are also equal. |
| Scalene | All sides and angles are different. |
Quadrilaterals
Quadrilaterals are four-sided polygons that come in various forms, such as squares, rectangles, parallelograms, and trapezoids. Each type has specific properties, including the number of parallel sides, angle relationships, and symmetry. For example, squares and rectangles have 90° angles, while parallelograms have opposite sides that are parallel and equal in length.
Properties of Quadrilaterals
| Type of Quadrilateral | Properties |
|---|---|
| Square | All sides equal, and all angles are 90°. |
| Rectangle | Opposite sides are equal, and all angles are 90°. |
| Parallelogram | Opposite sides are equal and parallel, and opposite angles are equal. |
| Trapezoid | One pair of opposite sides is parallel. |
Circles
The circle is a fundamental shape characterized by all points being equidistant from the center. The radius, diameter, and circumference are key measurements related to circles. The formula for the area of a circle is πr², and the circumference is 2πr, where r is the radius.
Properties of Circles
| Property | Formula/Description |
|---|---|
| Area | πr² |
| Circumference | 2πr |
| Diameter | 2r (twice the radius) |
| Preparation Tip | Description |
|---|---|
| Review Core Concepts | Focus on fundamental topics like shapes, angles, area, and important theorems. |
| Practice Under Test Conditions | Simulate the exam environment to practice time management and problem-solving. |
| Use Past Tests for Review | Identify strengths and weaknesses by practicing with past exam papers. |
| Manage Your Time | Allocate time for each section and avoid spending too long on difficult questions. |
| Stay Calm and Focused | Practice relaxation techniques and enter the exam with a positive mindset. |
By following these final preparation tips, you’ll be better equipped to perform at your best on exam day. Proper review, practice, and mental preparation are key components of success.