Linear Regression Exam Questions and Answers

In this section, we explore essential topics related to statistical models, focusing on the methods used to predict outcomes based on available data. These techniques are fundamental for anyone aiming to understand how relationships between variables are quantified and interpreted in various fields.

Mastering the techniques in this area is crucial for tackling related challenges in assessments. Whether you’re preparing for a test or just seeking to strengthen your knowledge, being familiar with the most common practices and pitfalls will greatly enhance your ability to analyze and interpret data accurately.

Effective preparation involves not only grasping the mathematical concepts but also being able to apply them to practical situations. By delving into key topics, learners can build a solid foundation for more advanced statistical analysis and improve their overall problem-solving skills.

Linear Regression Exam Questions and Answers

In any statistical assessment, it is important to have a clear understanding of key principles that help in making predictions based on datasets. This section provides an overview of common topics that you may encounter while preparing for tests related to statistical models. Gaining familiarity with these concepts will ensure you can confidently handle related challenges.

Key Concepts to Review

• Understanding the relationship between variables and how one predicts the other
• Interpreting coefficients and their significance in statistical modeling
• Knowing the importance of assumptions, such as normality and homoscedasticity
• Evaluating model performance through metrics like R-squared and residual plots

Common Practical Scenarios

• How to detect and handle multicollinearity in your dataset
• Steps to take when outliers affect model accuracy
• Methods for improving model fit when initial results are unsatisfactory
• Utilizing statistical software for efficient data analysis and interpretation

By focusing on these areas, you can better prepare for any related assessments and enhance your problem-solving abilities. Practicing with real-world data examples will help you sharpen your skills and approach similar challenges with confidence.

Key Concepts in Statistical Models

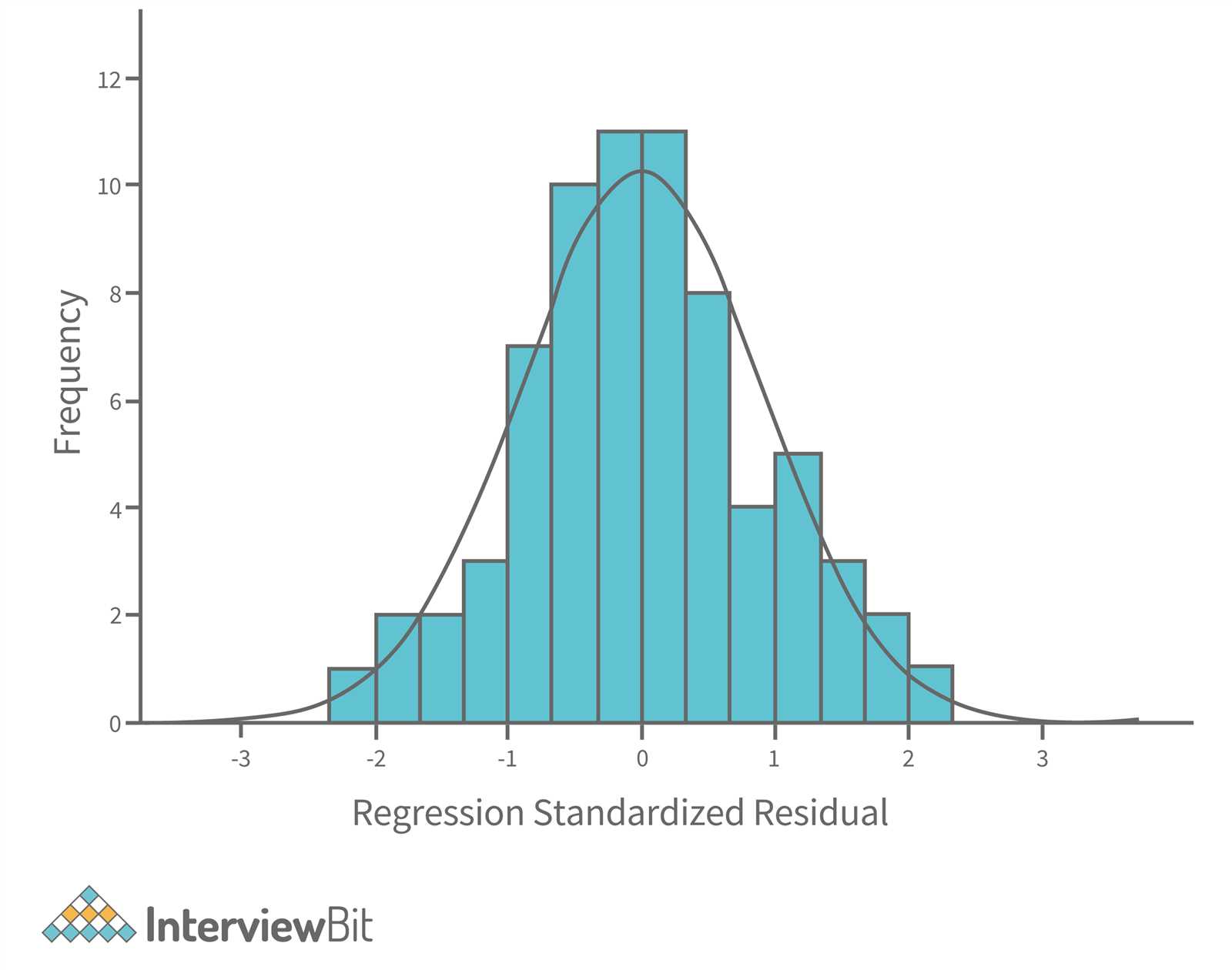
When analyzing datasets, it is essential to understand the foundational principles that underpin predictive models. These models rely on the relationship between variables to provide insights and predictions. Familiarizing yourself with these core ideas will help you navigate complex problems and improve your ability to interpret results accurately.

Essential Principles to Grasp

• The concept of dependent and independent variables in a dataset
• Interpreting the significance of coefficients in understanding relationships
• Knowing how to test assumptions about the data, such as normality or homoscedasticity
• Understanding the importance of residuals in assessing model fit

Important Metrics for Model Evaluation

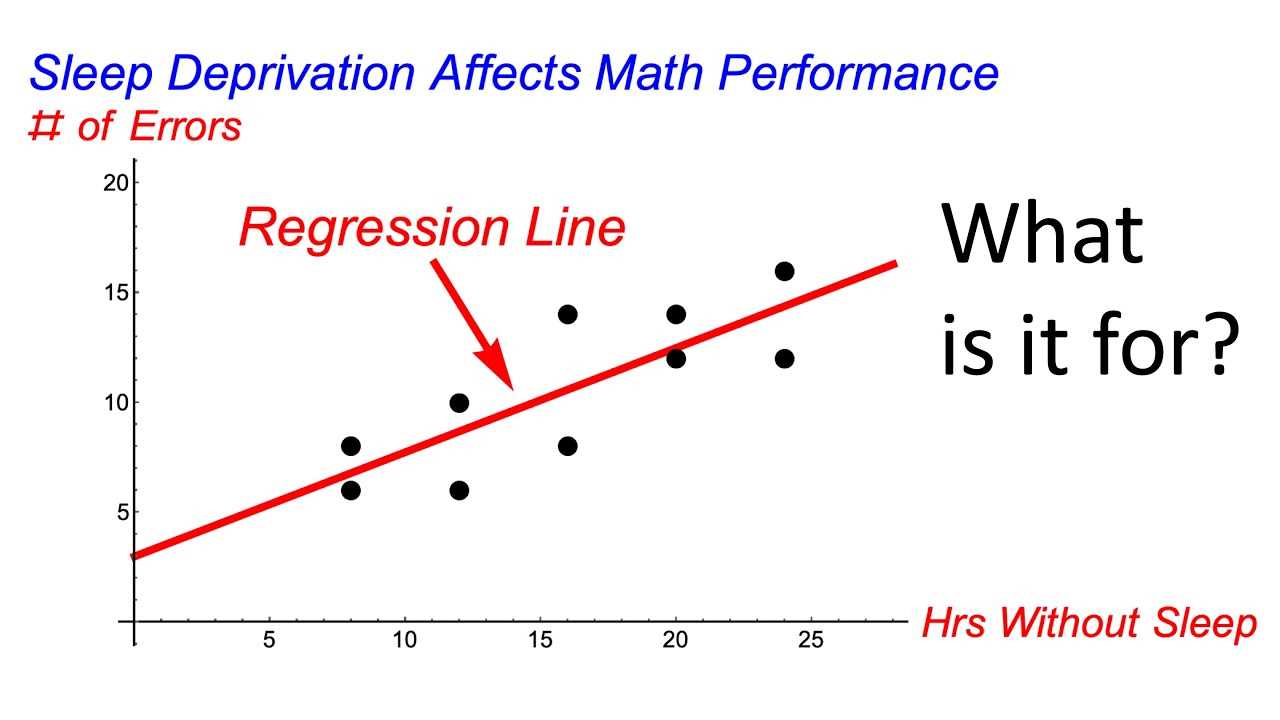
• R-squared: A measure of how well the model explains the variation in the data
• P-values: Used to determine the significance of coefficients
• Confidence intervals: Indicate the range within which the true value of a coefficient is likely to fall
• Standard errors: Help assess the precision of coefficient estimates

Mastering these concepts is key to building strong analytical skills and being able to assess the accuracy and reliability of your predictions. By understanding both the theory and practical application of these principles, you can tackle a wide range of statistical challenges with confidence.

Understanding Simple Models for Prediction

In statistical analysis, understanding basic predictive models is essential for drawing conclusions from data. These models aim to establish a relationship between two variables, where one is used to predict the other. Grasping the concept of a simple model helps build a foundation for more complex analyses and provides insights into how data can be used to make forecasts.

Key Elements of a Simple Predictive Model

• Dependent Variable: The variable that is being predicted or explained by the model.
• Independent Variable: The variable that is used to predict or explain the dependent variable.
• Equation: A mathematical representation that captures the relationship between the variables, typically in the form of a straight line.

Evaluating the Model’s Effectiveness

• Fit of the Model: This refers to how well the model captures the relationship between the variables, often assessed using measures like the coefficient of determination.
• Residuals: The differences between observed and predicted values, which help in evaluating the accuracy of the model.
• Interpretation of Coefficients: Understanding the influence of the independent variable on the dependent variable through the slope and intercept of the model’s equation.

Mastering simple models for prediction is critical for anyone analyzing data. These models provide valuable insights into how one factor influences another and form the basis for more complex analytical methods.

Interpreting Model Coefficients

In statistical analysis, understanding the coefficients of a model is crucial for interpreting how one variable influences another. These coefficients quantify the relationship between the independent and dependent variables, providing valuable insights into the strength and direction of that relationship. Proper interpretation allows analysts to draw meaningful conclusions and make informed predictions based on the model.

Understanding the Coefficient Values

• Intercept: This represents the expected value of the dependent variable when the independent variable is zero. It provides the starting point for the relationship between the variables.
• Slope: The slope indicates how much the dependent variable changes for a one-unit increase in the independent variable. A positive slope suggests a direct relationship, while a negative slope indicates an inverse relationship.
• Magnitude: The size of the coefficient tells you how strong the effect of the independent variable is on the dependent variable. Larger coefficients suggest a stronger influence.

Evaluating the Significance of Coefficients

• Statistical Significance: P-values are used to assess whether the coefficients are statistically significant, meaning the relationship they represent is unlikely to have occurred by chance.
• Confidence Intervals: These intervals provide a range within which the true coefficient value is likely to fall, offering a measure of precision for the estimates.
• Standard Errors: A smaller standard error indicates greater confidence in the coefficient estimate, whereas a larger error suggests more uncertainty.

By interpreting these coefficients correctly, you gain a deeper understanding of how the independent variable affects the outcome and can use this information for prediction and decision-making in practical scenarios.

Common Mistakes in Statistical Modeling

When working with predictive models, certain errors can significantly impact the reliability and accuracy of the results. Understanding these common pitfalls is essential for avoiding misinterpretation and ensuring that the conclusions drawn from the analysis are valid. This section highlights frequent mistakes that can arise during the modeling process.

Neglecting Assumptions

• Linearity: Assuming that the relationship between the variables is always linear, even when the data may suggest a different pattern.
• Independence: Failing to recognize that observations may not be independent, especially when dealing with time-series or clustered data.
• Homoscedasticity: Overlooking the assumption that the variance of the errors should remain constant across all levels of the independent variable.

Misinterpreting Results

• Overfitting: Creating a model that is too complex, capturing noise in the data instead of the underlying trend, leading to poor generalization on new data.
• Ignoring Multicollinearity: Failing to address the issue of highly correlated independent variables, which can distort the estimates and make interpretation difficult.
• Overemphasizing R-squared: Relying solely on R-squared to evaluate model fit, without considering other diagnostic measures like residuals or p-values.

Avoiding these common errors requires careful consideration of assumptions, thorough analysis, and an understanding of the limitations of the chosen model. By being aware of these pitfalls, analysts can produce more reliable and meaningful results.

How to Test Linearity Assumptions

When building predictive models, it is essential to test whether the relationship between variables follows the expected pattern. One of the fundamental assumptions in model building is that the connection between the variables is linear. Violations of this assumption can lead to biased or inaccurate results. In this section, we will discuss methods to check for the validity of this assumption and how to address potential issues.

Methods for Testing the Relationship

• Visual Inspection: Plotting the data and examining scatter plots between the independent and dependent variables can provide a quick indication of whether the relationship appears linear.
• Residual Plots: After fitting a model, analyzing the residuals can help identify if there are any non-linear patterns. If residuals show a systematic curve, the assumption may be violated.
• Correlation Tests: Performing statistical tests, such as the Pearson correlation, can help assess the strength and direction of the linear relationship.

Addressing Violations of Linearity

• Transformation of Variables: Applying mathematical transformations, such as logarithmic or polynomial functions, can help linearize a relationship.
• Non-Linear Models: In cases where the relationship is inherently non-linear, using models designed to handle complex relationships, like spline models or decision trees, can be more effective.

Summary of Linearity Tests

Test Method	Purpose	When to Use
Scatter Plots	Visualize the relationship between variables	Initial exploration of data
Residual Plots	Check if residuals show patterns	After fitting a model to data
Transformation	Adjust variables to linearize relationships	When a clear non-linear pattern is detected

By properly testing the assumption of linearity, you can ensure that the chosen model is valid and that your conclusions are accurate. Proper testing and adjustments allow for better-fitting models and more reliable predictions.

Difference Between Simple and Multiple Models

In predictive analysis, there are different approaches to modeling relationships between variables. One common distinction is between models that consider a single predictor and those that involve multiple predictors. While both types aim to explain the behavior of a dependent variable, the complexity and scope of each model differ significantly. Understanding the key differences between these two approaches is essential for selecting the appropriate model for a given dataset.

Simple Model

A simple model involves only one independent variable to predict the dependent variable. This model is typically used when the relationship between the two variables appears straightforward and uncomplicated. The focus is on how changes in the single predictor affect the outcome.

• Only one independent variable is considered
• Used when the relationship between variables is expected to be direct
• Ideal for straightforward predictions

Multiple Model

In contrast, a multiple model incorporates two or more independent variables. This approach is more flexible, allowing for the analysis of complex interactions between several predictors. It is particularly useful when multiple factors contribute to the outcome, and their combined influence needs to be assessed.

• Involves two or more independent variables
• Can model more complex relationships with multiple contributing factors
• Helps capture interactions between different predictors

Choosing between a simple and a multiple model depends on the data and the research question. Simple models are useful for analyzing straightforward relationships, while multiple models offer a more detailed and nuanced understanding when multiple factors are at play.

Evaluating Model Fit with R-Squared

Assessing the quality of a predictive model is a key step in any data analysis process. One of the most common metrics used to evaluate how well a model fits the data is the coefficient of determination, often referred to as R-squared. This value provides insight into the proportion of variance in the dependent variable that can be explained by the independent variables. However, it is important to understand both the strengths and limitations of this measure when interpreting model performance.

Understanding R-Squared

R-squared is a statistical measure that indicates the goodness of fit of a model. It ranges from 0 to 1, where a value closer to 1 suggests that the model explains a high proportion of the variance in the data, and a value closer to 0 indicates a poor fit. An R-squared value of 1 means the model perfectly fits the data, while a value of 0 means the model does not explain any of the variability.

• High R-Squared: A higher value generally suggests a better fit, but this does not always mean the model is the best choice for prediction.
• Low R-Squared: A low value may indicate that important variables are missing from the model or that the data is too noisy for a reliable prediction.

Limitations of R-Squared

While R-squared is a useful tool, it has several limitations. For example, it can increase with the inclusion of more independent variables, even if those variables do not improve the model’s predictive power. Therefore, relying solely on R-squared to assess model quality can be misleading. It is often advisable to complement it with other metrics, such as adjusted R-squared, AIC, or cross-validation, to get a more comprehensive evaluation of model performance.

• Adjusted R-Squared: This metric adjusts the R-squared value by penalizing the addition of unnecessary variables, offering a more accurate picture of model fit.
• Cross-Validation: This technique involves splitting the data into subsets to assess how well the model generalizes to new data.

In conclusion, R-squared is a helpful tool for evaluating model fit, but it should be interpreted carefully in the context of other performance measures to avoid overfitting or misinterpretation of results.

Significance of P-Values in Regression

In statistical modeling, one of the key aspects to assess is whether the relationships between variables are statistically significant. The p-value is a crucial measure used to determine the strength of evidence against a null hypothesis. Understanding the role of p-values helps in making informed decisions about which predictors should be included in a model and which should be excluded.

A p-value represents the probability of obtaining results at least as extreme as the ones observed, assuming the null hypothesis is true. In the context of predictive models, the null hypothesis typically suggests that there is no relationship between the independent variable and the dependent variable. A smaller p-value indicates stronger evidence against the null hypothesis, suggesting that the independent variable has a meaningful effect on the outcome.

• Small P-Value (typically less than 0.05): This suggests strong evidence against the null hypothesis, meaning the variable is likely a significant predictor of the outcome.
• Large P-Value (greater than 0.05): This suggests weak evidence against the null hypothesis, implying that the variable may not be a significant predictor of the outcome.

However, p-values should not be used in isolation to make final decisions. It is important to consider other factors, such as the effect size and the context of the data, when interpreting p-values. Additionally, in complex models with multiple predictors, the interpretation of p-values can become more nuanced, and adjustments may be necessary to avoid misinterpretations, such as in the case of multiple comparisons.

Multicollinearity and Its Impact on Results

In statistical modeling, it is important to ensure that the predictors included in the model do not exhibit high levels of correlation with one another. When multiple predictors are highly correlated, it can lead to unreliable or unstable estimates of the relationships between variables. This phenomenon, known as multicollinearity, can significantly affect the validity of a model’s results.

Multicollinearity occurs when two or more independent variables in a model are highly correlated, making it difficult to distinguish their individual effects on the dependent variable. This can lead to several issues, such as inflated standard errors and unstable coefficient estimates, which in turn affect the model’s interpretability and predictive accuracy.

• Inflated Standard Errors: Multicollinearity causes the variance of the coefficient estimates to increase, which means that the estimates are less precise. This makes it harder to assess the significance of each predictor.
• Unstable Coefficients: When predictors are highly correlated, small changes in the data can result in large changes in the coefficient estimates, leading to unreliable conclusions.

It is crucial to detect and address multicollinearity to ensure the robustness of the model. Techniques such as variance inflation factor (VIF) analysis or correlation matrices can be used to assess the degree of multicollinearity. When high multicollinearity is detected, steps like removing redundant variables or combining predictors may be necessary to improve model stability and interpretability.

Residual Analysis in Regression Models

Residual analysis is an essential step in evaluating the adequacy of a model’s fit to the data. By examining the difference between the observed values and the predicted values, analysts can identify patterns, inconsistencies, and any potential violations of assumptions made by the model. This process helps in determining whether the model is appropriate for the data and whether any adjustments are necessary.

Understanding Residuals

Residuals are the differences between the observed values of the dependent variable and the values predicted by the model. These discrepancies provide valuable information about how well the model captures the underlying relationships in the data. Ideally, residuals should be randomly distributed with no discernible pattern, indicating that the model is a good fit.

• Positive Residuals: Occur when the model underestimates the observed value.
• Negative Residuals: Occur when the model overestimates the observed value.
• Zero Residuals: Indicate that the model perfectly predicts the observed values (though this is rare in practice).

Identifying Model Issues Through Residuals

By plotting residuals or examining their distribution, analysts can detect several potential problems with the model:

• Non-random Patterns: If residuals display a systematic pattern (such as curves or trends), it may indicate that the model is missing key variables or that a non-linear relationship exists between the predictors and the outcome.
• Non-constant Variance (Heteroscedasticity): If the spread of residuals increases or decreases with the predicted values, this suggests that the variance of errors is not constant, violating one of the key assumptions of many models.
• Outliers: Residual analysis can also help in detecting outliers or influential points that disproportionately affect the model’s estimates.

Addressing issues identified through residual analysis often involves refining the model, such as adding missing variables, transforming data, or reconsidering the type of model used. Regularly conducting residual analysis ensures that the model remains accurate and robust, leading to more reliable predictions and inferences.

Handling Outliers in Regression Analysis

Outliers are data points that deviate significantly from the rest of the dataset. These unusual observations can have a considerable impact on the accuracy and validity of a model. Identifying and appropriately addressing outliers is essential to ensure that the model remains reliable and the results meaningful. In many cases, outliers can distort statistical analysis, leading to misleading conclusions if not handled correctly.

Identifying Outliers

Outliers can be identified using various methods, such as visual inspection of scatter plots, residual plots, or by calculating standardized residuals. A common rule of thumb is that values greater than 3 standard deviations from the mean may be considered outliers. Additionally, boxplots and other statistical techniques like the Z-score or IQR method can help pinpoint data points that fall outside the expected range.

Method	Description	Criteria for Outliers
Standard Deviation	Measures how far a data point is from the mean	Data points beyond 3 standard deviations
Boxplot	Visual representation of data distribution	Points beyond 1.5 * IQR (Interquartile Range)
Z-score	Measures the number of standard deviations away from the mean	Z-score > 3 or

Dealing with Outliers

Once outliers are identified, there are several approaches to deal with them:

• Excluding Outliers: If outliers are caused by errors or irrelevant observations, they can be removed from the dataset to prevent distortion of the analysis.
• Transforming Data: Applying transformations (such as log or square root) can reduce the impact of outliers and make the data more normally distributed.
• Using Robust Methods: Some statistical models, such as robust regression, are less sensitive to outliers and can be used to mitigate their effect on the model’s estimates.
• Winsorizing: This involves capping extreme values to a certain percentile, reducing their influence while keeping them in the dataset.

It is important to assess whether outliers are genuine observations or data errors before deciding how to handle them. Ignoring them without careful consideration can lead to inaccurate results, while removing valuable data points can risk losing important insights.

Step-by-Step Guide to Regression Calculation

Performing calculations for a statistical model involves several steps that allow us to understand the relationship between variables. Whether you are working with a single predictor or multiple, the process involves collecting data, fitting the model, and interpreting the results. The following guide provides a structured approach to perform these calculations, ensuring accuracy and clarity at each stage.

1. Gather Data

The first step is to collect the data that will be used for analysis. It’s important to ensure that the dataset is clean, complete, and free of errors. Each observation should include all the necessary variables for analysis. Typically, one variable will be the dependent (or outcome) variable, and the other(s) will be independent (predictor) variables.

2. Plot the Data

Visualizing the data helps in understanding the relationship between the variables. A scatter plot can be used to check if there is a linear trend or other patterns. This step provides insight into whether the assumptions of the model are likely to hold, and can help identify any outliers or influential data points.

3. Calculate the Slope and Intercept

The next step is to calculate the coefficients for the model. For simple models, the slope and intercept are the key parameters that define the best-fit line. These values can be calculated using formulas such as:

• Slope: b = Σ((X – X̄)(Y – Ŷ)) / Σ(X – X̄)^2
• Intercept: a = Ŷ – bX̄

Where X̄ and Ŷ represent the mean of the independent and dependent variables, respectively, and b is the slope, which quantifies the change in Y for a one-unit change in X.

4. Calculate the Predicted Values

Once the slope and intercept are calculated, you can determine the predicted values for the dependent variable using the model equation. For each data point, the predicted value Ŷ is calculated as:

• Ŷ = a + bX

Where a is the intercept, b is the slope, and X is the value of the independent variable for which the prediction is being made.

5. Evaluate the Model Fit

Once the predictions are made, it’s important to assess how well the model fits the data. This is typically done by calculating the residuals, which are the differences between the observed and predicted values. A smaller residual indicates a better model fit. You can also calculate the coefficient of determination (R-squared) to measure the proportion of variance explained by the model.

6. Interpret the Results

After performing the calculations, the next step is to interpret the results. The slope tells you how much change in the dependent variable is expected with each unit change in the independent variable. The intercept provides the expected value of the dependent variable when the independent variable is zero. Additionally, statistical significance (usually checked through p-values) helps determine whether the model coefficients are reliable.

7. Validate the Assumptions

Before finalizing your model, it’s essential to validate the assumptions of the analysis. This includes checking for normality of residuals, linearity of relationships, independence of errors, and constant variance of residuals (homoscedasticity). If these assumptions are violated, adjustments may be needed, such as transforming variables or using more advanced modeling techniques.

8. Report the Findings

Finally, summarize the findings in a clear and concise manner. Present the coefficients, statistical significance, and model evaluation metrics like R-squared. You may also provide a visual representation, such as a line of best fit, to make the results more accessible to your audience.

By following these steps, you can calculate, evaluate, and interpret the results of a statistical model, providing valuable insights into the relationship between variables and helping to make informed decisions based on the data.

Using Statistical Software for Linear Regression

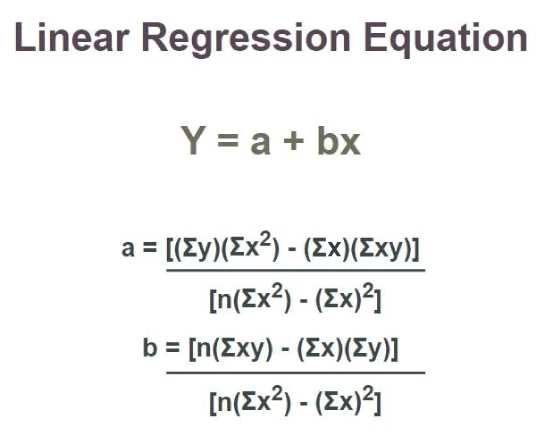
Statistical software offers powerful tools for analyzing relationships between variables, streamlining the entire process of data modeling. By automating calculations and providing advanced visualizations, these programs help users quickly interpret results and make informed decisions. Utilizing such tools allows for more efficient handling of large datasets and complex analyses, making them invaluable for anyone involved in statistical modeling.

1. Selecting the Right Software

Choosing the appropriate software is the first step in conducting a thorough analysis. Popular options such as R, Python, SPSS, and SAS each offer distinct features that cater to different needs. R and Python are highly flexible and widely used for custom models and advanced analyses, while SPSS and SAS provide user-friendly interfaces ideal for quick statistical tests and standard modeling techniques.

2. Inputting Data into Software

Once you’ve selected the software, the next step is to import your dataset. Most programs allow you to input data from various sources, including CSV files, Excel spreadsheets, or even direct connections to databases. It’s essential to check that the data is formatted correctly, with the dependent and independent variables properly labeled for analysis.

3. Running the Analysis

Running the analysis in statistical software typically involves selecting the appropriate model type and specifying the variables involved. In most cases, this is done by choosing the dependent variable (the outcome you want to predict) and one or more independent variables (the predictors). Software like R and Python offers extensive libraries, such as lm() in R or statsmodels in Python, to carry out the necessary calculations.

4. Interpreting the Output

After executing the model, statistical software will generate output containing key metrics such as coefficients, standard errors, t-statistics, and p-values. The software also typically provides goodness-of-fit measures like R-squared and visual outputs like scatter plots with fitted lines. These results help you assess the relationship between variables and determine whether the model is statistically significant.

5. Troubleshooting and Refining the Model

Even after running the analysis, it’s essential to examine the results for possible issues. For example, you might need to address multicollinearity, check for outliers, or consider transformations to better meet model assumptions. Statistical software can also assist with residual analysis and diagnostics, allowing you to refine the model for better accuracy and reliability.

By using statistical software, you streamline the process of model creation, evaluation, and refinement, ensuring a thorough analysis with minimal manual calculation. These tools save time and improve the precision of your analysis, making them indispensable for data scientists, statisticians, and analysts.

Regression Diagnostics for Better Predictions

Accurate predictions rely not only on building a model but also on ensuring that the model meets the necessary assumptions and accurately reflects the relationships between variables. Diagnostic techniques play a vital role in identifying potential issues in the model, such as violations of assumptions or outliers that could distort results. By performing these checks, you can refine your model for improved accuracy and reliability in predictions.

1. Residual Analysis

Examining the residuals, or the differences between observed and predicted values, is a crucial diagnostic tool. A good model will have residuals that are randomly scattered around zero, indicating no patterns or biases. If there are patterns in the residuals, it suggests that the model has missed important information. Residual analysis helps to check for:

• Heteroscedasticity: Non-constant variance of residuals.
• Non-linearity: The relationship between variables may not be properly captured.
• Autocorrelation: Residuals from one observation are correlated with another.

2. Checking for Multicollinearity

Multicollinearity occurs when two or more predictors are highly correlated with each other. This can cause instability in the estimated coefficients, making them difficult to interpret. To detect multicollinearity, you can calculate the Variance Inflation Factor (VIF) for each predictor. A high VIF (greater than 10) indicates multicollinearity, which may require you to remove or combine variables.

3. Influence and Leverage

Influence refers to how much a single data point can affect the overall results of the model. High-leverage points, or outliers, can disproportionately affect the slope of the fitted line. Using measures like Cook’s Distance and leverage statistics, you can identify influential data points that might be distorting the results. After identifying them, you can decide whether to remove these points or adjust the model accordingly.

4. Normality of Errors

Many statistical techniques assume that the errors (residuals) are normally distributed. Checking for normality helps ensure the reliability of statistical tests and confidence intervals. A histogram or Q-Q plot can visually assess normality, while statistical tests such as the Shapiro-Wilk test provide more formal checks. Non-normal residuals may suggest the need for a data transformation.

5. Model Specification Errors

Model specification errors occur when the model incorrectly represents the relationship between variables. This can happen if important predictors are omitted or if irrelevant variables are included. It is crucial to carefully consider the variables and the form of the model to ensure accurate results. Diagnostic tests like the Ramsey RESET test can help identify model specification issues.

By conducting thorough diagnostics, you can uncover hidden issues and improve the performance of your predictive model. This ensures that your model produces reliable forecasts and is robust enough to handle real-world data variations.

Common Inquiries on Modeling Techniques

When preparing for assessments on statistical models, it is essential to focus on the core concepts and application methods that are commonly tested. These evaluations often address the understanding of model creation, interpretation of results, and the assumptions behind the methodology. Below are some frequently asked topics related to statistical models that involve predictive relationships between variables.

1. What is the purpose of the coefficient of determination in model evaluation?

The coefficient of determination is a key metric used to measure how well the model fits the observed data. It represents the proportion of the variance in the dependent variable that is predictable from the independent variables. Understanding its value helps in assessing the effectiveness of the model and the strength of the relationship between the variables. A higher value indicates a better fit, whereas a lower value suggests a poor model performance.

2. How do you interpret the coefficients of a fitted model?

The coefficients represent the relationship between each predictor and the outcome. For each unit change in a predictor, the coefficient quantifies the expected change in the dependent variable. Interpreting these values is crucial for understanding the impact of each variable in the context of the model. Positive coefficients indicate a direct relationship, while negative coefficients suggest an inverse relationship.

3. What is multicollinearity, and why is it problematic?

Multicollinearity refers to the situation where two or more predictors in the model are highly correlated with each other. This issue can lead to unstable estimates of the coefficients, making it difficult to determine the individual effect of each predictor. It may inflate standard errors and cause misleading statistical significance results, reducing the reliability of the model.

4. How do you check for homoscedasticity in your model?

Homoscedasticity is the assumption that the variance of errors is constant across all levels of the independent variable. To check for homoscedasticity, residual plots can be used. If the plot shows a random scatter with no pattern, the assumption is met. However, if the plot shows a funnel shape or other patterns, it indicates heteroscedasticity, which may require transformation of the data or the use of robust standard errors.

5. What are the assumptions behind a typical model?

Several assumptions are made when building a predictive model. These include the linearity of relationships, independence of errors, normal distribution of residuals, and constant variance of errors (homoscedasticity). Violations of these assumptions can lead to biased or inefficient estimates, and it is important to verify them through diagnostic tests before drawing conclusions from the model.

6. What is the significance of the p-value in interpreting model results?

The p-value helps determine the statistical significance of each predictor in the model. A low p-value (typically below 0.05) suggests that the predictor is significantly associated with the outcome variable, while a high p-value suggests that the predictor may not have a significant effect. However, it is important to consider the context and the overall model fit when interpreting p-values.

Understanding these concepts is critical for mastering statistical techniques and successfully navigating assessments on the subject. By focusing on these common inquiries, you can strengthen your grasp of the material and be well-prepared for any evaluation.

How to Prepare for Predictive Modeling Tests

Preparing for assessments that focus on statistical models requires a solid understanding of the fundamental principles and practical techniques. The key to success is mastering the steps involved in model development, interpretation, and validation. By focusing on the core elements and practicing with real data sets, you can ensure that you are ready to demonstrate your knowledge and skills. Below are several strategies to help you effectively prepare for such tests.

1. Review Key Concepts and Terminology

Before diving into the practical aspects, ensure that you are familiar with essential terms and concepts. These include understanding the relationships between variables, the significance of model parameters, the role of residuals, and the assumptions behind the model. A strong grasp of these concepts will help you interpret results and identify potential issues during the testing process. Focus on the meaning of coefficients, the impact of predictors, and how to evaluate model fit using various metrics.

2. Practice with Real Data

Theory is important, but hands-on experience is equally crucial. Work through practical examples and exercises to familiarize yourself with model building and testing procedures. Using statistical software or coding environments, practice applying models to real-world datasets. This will not only help reinforce theoretical concepts but also allow you to develop troubleshooting skills when faced with issues such as multicollinearity, heteroscedasticity, or non-linearity. Pay attention to the assumptions underlying each model and practice diagnosing and addressing violations.

By actively engaging with the material and applying it to different scenarios, you will build the confidence needed to excel in predictive modeling assessments. Understanding the theory, practicing your skills, and learning how to interpret results will ensure you are well-prepared for the test.