Preparing for a test that involves numerical analysis requires a solid understanding of various principles and techniques. Whether you’re dealing with raw data, working through probability scenarios, or applying mathematical models, having a clear approach to problem-solving is key to success. This guide aims to provide essential insights into how to navigate through typical problems and how to enhance your performance during assessment sessions.
When tackling these types of assessments, it’s important to focus on the core elements that often appear in various forms. Recognizing patterns and understanding how to apply the right methods can make a significant difference. With proper preparation, you will be able to break down complex tasks and solve them with confidence, using the strategies outlined here.
By honing your skills in interpreting information and applying the appropriate techniques, you’ll be well-equipped to tackle a variety of challenges. Understanding the structure of typical problems will not only help you perform better but also build your confidence for future evaluations. Keep practicing, and you’ll see improvements in both speed and accuracy.
Understanding Common Test Problem Types
During assessments focused on numerical reasoning, students encounter a range of problem types that test their grasp of fundamental concepts. These problems can vary in format, requiring different approaches to find solutions. Recognizing the structure of these problems can greatly improve one’s ability to respond efficiently and accurately under time pressure.
One common type involves identifying key data points and using them to compute specific values, such as averages, variances, or correlations. These problems may present raw information in the form of tables or graphs, requiring candidates to interpret and manipulate the data accordingly. Another frequent category tests the ability to apply theoretical models to solve practical challenges, such as predicting outcomes based on established formulas.
Types of Problems You May Encounter
| Problem Type | Description | Key Skills Required |
|---|---|---|
| Descriptive Tasks | Interpret and summarize given datasets. | Data analysis, averages, measures of dispersion |
| Inference Tasks | Draw conclusions based on sample data. | Hypothesis testing, confidence intervals |
| Problem-Solving Tasks | Apply models or formulas to solve practical scenarios. | Mathematical reasoning, formula application |
Preparing for Different Problem Types
Familiarity with these problem formats is essential. The more you practice, the more you’ll be able to identify the most effective methods for each type. Developing a systematic approach will help ensure you stay organized and focused, improving both speed and accuracy.
How to Approach Data Interpretation Questions
When tasked with analyzing data presented in various formats, it’s crucial to understand the underlying patterns and relationships. The key to solving these challenges lies in breaking down the information systematically, ensuring that every relevant detail is carefully considered. This section will guide you through effective strategies for tackling problems that involve extracting meaningful insights from complex datasets.
The first step in handling such problems is to examine the structure of the provided data. Whether it’s in the form of a table, graph, or chart, identifying the variables and their connections will allow you to form an initial understanding of what the data represents. Once familiarized with the layout, proceed by focusing on the specific values or trends that the task asks you to interpret or calculate.
Key Steps for Effective Interpretation
| Step | Action | Example |
|---|---|---|
| Step 1 | Examine the structure of the data set. | Identify columns, rows, and units of measurement in a table. |
| Step 2 | Highlight important trends or values. | Look for outliers or patterns in a graph. |
| Step 3 | Analyze the relationships between variables. | Assess how one factor impacts another, such as income vs. education level. |
Common Pitfalls to Avoid
One of the most common mistakes is overlooking key information that may seem insignificant at first glance. Ensure that every detail–whether it’s a label, unit, or value–is accounted for in your analysis. Another challenge is misinterpreting the data due to a failure to understand its context. Always refer to the task’s instructions or question to ensure you’re focusing on the right aspect of the data.
Common Pitfalls in Assessments
While solving numerical reasoning tasks, students often face challenges that can lead to mistakes, even when they understand the core concepts. Identifying and avoiding these common pitfalls can make a significant difference in overall performance. Many errors stem from oversights, misinterpretation of instructions, or improper application of methods, which can be easily prevented with the right approach.
One frequent issue is rushing through problems without fully understanding what is being asked. This can lead to skipping crucial steps, missing important details, or applying the wrong techniques. Another common mistake is misinterpreting data or overlooking key values, which can skew results and lead to incorrect conclusions. In these situations, it’s essential to slow down and review each part of the task carefully before proceeding.
Key Mistakes to Avoid
| Error | How to Avoid It | Example |
|---|---|---|
| Rushing through calculations | Double-check each step and take time to read instructions carefully. | Skipping the units or miscalculating totals. |
| Misunderstanding the task | Read the prompt thoroughly to identify exactly what is being asked. | Focusing on irrelevant details or solving the wrong problem. |
| Overlooking critical data | Review the entire dataset to identify all important values or patterns. | Missing outliers or significant trends in graphs. |
Strategies for Success
To avoid these pitfalls, practice is essential. Regularly working through sample problems and time-limited tasks can help you develop a more methodical approach and improve your accuracy. Always prioritize understanding the task at hand and verifying your results at each stage to ensure the highest level of precision.
Effective Study Techniques for Exam Success

Achieving success in assessments requires more than just understanding the material. Effective preparation involves a mix of strategies that help reinforce knowledge, improve recall, and build confidence. By incorporating the right techniques, students can enhance their learning and perform at their best during the test.
One of the most important study techniques is active learning. Instead of passively reading through notes, engage with the material by practicing problems, teaching concepts to others, or creating mind maps to visualize relationships. Repetition also plays a crucial role in solidifying knowledge and reinforcing key concepts.
Key Techniques for Efficient Studying
- Practice Regularly: Solve practice problems regularly to strengthen your problem-solving skills.
- Use Active Recall: Test your understanding by recalling information without looking at your notes.
- Break Study Sessions into Intervals: Use techniques like the Pomodoro method to study in focused intervals with short breaks in between.
- Teach What You Learn: Explaining concepts to others helps reinforce your understanding.
Creating a Study Schedule

A well-structured study schedule is essential to avoid last-minute cramming. Break down the material into manageable sections and allocate time for each topic. Prioritize areas where you feel less confident, while still reviewing familiar concepts to keep them fresh. Consistency and time management will help you stay on track and reduce stress as the test approaches.
- Set Clear Goals: Define what you want to achieve in each study session.
- Review Regularly: Schedule time for weekly reviews to reinforce what you’ve learned.
- Simulate Test Conditions: Practice under timed conditions to improve speed and accuracy.
By adopting these effective study strategies, you’ll be better prepared, more focused, and ultimately more successful in your assessments.
Understanding Probability Problems
Probability-related problems often require a deep understanding of how events and outcomes are connected. These tasks assess your ability to calculate the likelihood of various outcomes based on given data. It’s important to break down the problem systematically, identifying all possible scenarios and the relationships between them. Understanding key concepts, such as independent and dependent events, can make it easier to approach and solve these types of tasks efficiently.
In many cases, probability problems involve calculating the likelihood of a specific event occurring within a defined set of possibilities. These problems might ask you to work with either theoretical or empirical data, and recognizing the correct formula or method to apply is crucial. Whether dealing with simple events or more complex compound scenarios, the key is to focus on understanding the underlying principles and applying them to find the solution.
Key Concepts in Probability
- Independent Events: Two events that do not influence each other’s outcome.
- Dependent Events: When the occurrence of one event affects the probability of another.
- Complementary Events: Two outcomes that are mutually exclusive and cover all possibilities.
- Conditional Probability: The probability of an event occurring given that another event has already occurred.
Steps for Solving Probability Problems
To approach probability tasks effectively, follow a systematic method:
- Understand the Event: Clearly define what event you are calculating the probability for.
- Identify Possible Outcomes: List all possible outcomes and ensure no possibilities are overlooked.
- Use the Correct Formula: Depending on the task, use the appropriate formula to calculate the probability.
- Double-Check Your Work: Verify that your calculations make sense in the context of the problem.
With practice and a thorough understanding of these principles, probability problems become much easier to solve and less intimidating during assessments.
How to Solve Regression Analysis Problems
Regression analysis tasks typically involve understanding the relationship between two or more variables and making predictions based on that relationship. These problems assess your ability to apply mathematical models to real-world data, identifying patterns and trends. Solving such tasks requires a logical approach, where the goal is to accurately model the connection between variables and determine how one affects the other.
The first step in tackling regression challenges is understanding the data and identifying which variables are dependent and which are independent. Once you have a clear understanding of the data structure, you can proceed with selecting the appropriate regression method. Whether you’re dealing with simple linear regression or more complex multiple regression, each method has its own set of assumptions and steps to follow.
Steps to Solve Regression Problems

- Understand the Data: Examine the given dataset and identify the key variables, determining which one is dependent and which are independent.
- Choose the Right Regression Model: Select the appropriate method based on the number of variables and the nature of the data (e.g., simple linear regression, multiple regression, or logistic regression).
- Calculate the Regression Equation: Use the chosen method to calculate the regression equation, which models the relationship between the variables.
- Interpret the Results: Analyze the coefficients and other statistical outputs (e.g., R-squared, p-values) to understand the strength and significance of the relationships.
- Make Predictions: Use the regression equation to make predictions based on new input values or to assess the accuracy of the model.
Common Mistakes to Avoid
- Overlooking Assumptions: Ensure that the data meets the assumptions of the chosen regression model, such as linearity or normality of residuals.
- Misinterpreting Coefficients: Be cautious when interpreting the regression coefficients, as they represent the relationship between independent and dependent variables.
- Neglecting Model Evaluation: Always evaluate the model’s performance using metrics like R-squared or adjusted R-squared to ensure it accurately fits the data.
By following these steps and avoiding common pitfalls, you can effectively solve regression analysis problems and apply them to real-world data to make informed predictions.
Descriptive Statistics: Key Formulas to Know
When analyzing data, it’s crucial to summarize and describe its main features efficiently. Understanding and applying key formulas allows for the effective organization and interpretation of data sets. These formulas help quantify central tendencies, variability, and the overall distribution of the data, providing insights into patterns and trends that may otherwise go unnoticed.
There are several essential calculations that form the foundation for descriptive analysis. These formulas are used to determine measures like the average, the spread of data, and the relationship between different values in the dataset. Mastering these will ensure that you can quickly interpret results and draw meaningful conclusions from any dataset.
Important Measures and Formulas

| Measure | Formula | Description |
|---|---|---|
| Mean | μ = Σx / n | Sum of all values divided by the number of values. |
| Median | Middle value of ordered data | The middle value when the data is sorted in ascending order. |
| Mode | Most frequent value | The value that appears most often in the dataset. |
| Variance | σ² = Σ(x – μ)² / n | Measure of the spread of data points from the mean. |
| Standard Deviation | σ = √(Σ(x – μ)² / n) | Square root of the variance, indicating how spread out the data is. |
How to Apply These Formulas
To calculate the mean, simply add all values in the data set and divide by the number of entries. The median is found by sorting the data in ascending order and selecting the middle value, while the mode is the most frequently occurring number. Variance and standard deviation measure the spread of the data, with standard deviation providing a more intuitive understanding of variability by being in the same units as the original data.
Understanding these basic formulas is essential for summarizing data effectively, whether you’re conducting research or solving related tasks. Mastery of these concepts provides a solid foundation for more advanced techniques and ensures accuracy in data interpretation.
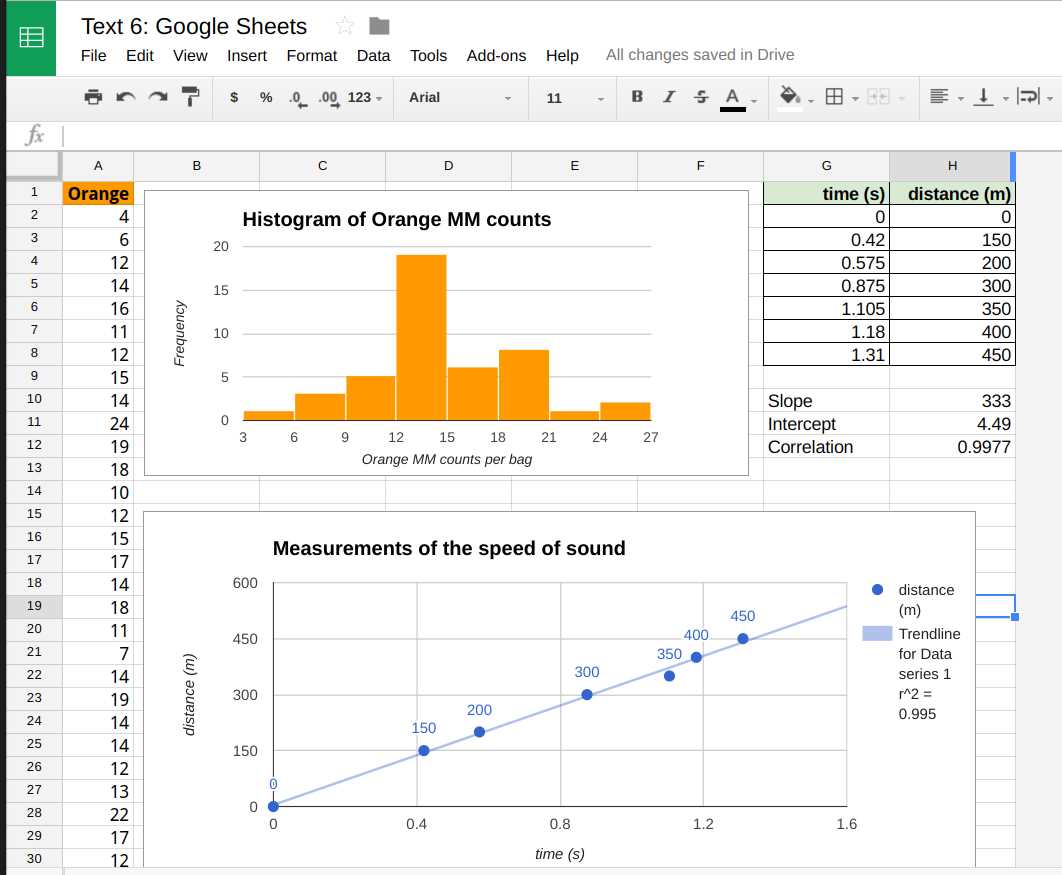
Interpreting Graphs and Charts in Assessments
Visual representations of data, such as graphs and charts, are commonly used to convey complex information in a clear and concise manner. These tools allow for the quick identification of patterns, trends, and relationships between variables. Being able to accurately interpret these visuals is crucial for understanding the underlying data and making informed conclusions.
When analyzing graphs or charts, it’s important to first identify the type of visual representation used, whether it’s a bar chart, pie chart, line graph, or histogram. Each type provides different insights and is suited for specific kinds of data. After identifying the chart type, focus on understanding the axes, labels, and data points, as well as any trends or deviations that appear. This will help you extract the most relevant information to answer related tasks.
Key Steps to Interpret Graphs and Charts
- Identify the Chart Type: Determine whether it’s a bar chart, line graph, pie chart, etc., to understand what kind of data is being presented.
- Examine the Axes: Check the labels on both axes to understand what variables are being compared and their corresponding units of measurement.
- Analyze Data Points: Look at the data points to identify trends, patterns, or outliers in the chart.
- Look for Key Features: Pay attention to any trends, peaks, or declines that might indicate a significant relationship between the variables.
- Draw Conclusions: Based on your observations, make inferences or predictions about the data represented in the graph or chart.
By following these steps, you can quickly interpret visual data and apply it effectively to answer related questions or solve problems during assessments.
Tips for Time Management During Assessments
Effectively managing time during an assessment is essential for maximizing performance and ensuring all tasks are completed within the allotted time frame. Procrastination or rushing through tasks can lead to mistakes or unfinished work. A structured approach to time management helps prioritize important sections, reduce stress, and improve overall efficiency.
To manage your time well, it’s crucial to plan ahead, stay organized, and know when to move on from a challenging problem. By following strategic steps, you can stay on track and ensure that each section receives the attention it requires.
Effective Time Management Strategies
- Read Instructions Carefully: Before starting, take a few minutes to read through all instructions to ensure you understand the tasks and requirements.
- Allocate Time for Each Section: Break down the available time and assign specific portions for each part of the assessment based on its complexity and points.
- Start with Easier Tasks: Begin with the questions you feel most confident about to build momentum and ensure quick wins early on.
- Set Time Limits: Use a watch or clock to monitor the time for each task. Avoid spending too much time on a single question, and move on if you’re stuck.
- Leave Time for Review: Reserve the final few minutes to review your answers for any mistakes or unfinished sections. This ensures accuracy and helps catch errors.
How to Handle Unexpected Challenges
- Don’t Panic: If a question is too difficult, stay calm. Skip it temporarily and return after completing the easier ones to maintain your momentum.
- Use a Systematic Approach: If time is running short, systematically address key points of each task rather than attempting to complete every single detail.
- Prioritize High-Value Sections: Focus on the sections that carry the most points, ensuring that you give them adequate time for a thorough response.
By implementing these time management techniques, you can approach assessments with greater confidence, reduce anxiety, and increase your chances of achieving better results.
How to Handle Hypothesis Testing Questions

When addressing tasks related to testing assumptions, it is crucial to follow a clear, step-by-step approach. These tasks often involve evaluating a claim or hypothesis by using sample data and determining whether the evidence is sufficient to support or reject the initial assumption. The key to success lies in understanding the process and applying it methodically to make informed conclusions.
The process typically begins with defining the null and alternative hypotheses, followed by choosing the appropriate test statistic and significance level. Then, based on sample data, you perform calculations to assess whether the results indicate statistical significance. By approaching these tasks with precision and clarity, you can confidently draw conclusions about the data.
Steps to Effectively Solve Hypothesis Testing Problems
- State the Hypotheses: Clearly define the null hypothesis (H₀) and the alternative hypothesis (H₁). The null hypothesis usually represents no effect or no difference, while the alternative suggests the presence of an effect or difference.
- Select the Test: Choose the appropriate test based on the data type (e.g., t-test, chi-square test, ANOVA). Make sure the test fits the research question and data characteristics.
- Set the Significance Level: Determine the threshold (commonly 0.05) that will be used to decide whether to reject the null hypothesis. This is your alpha level (α).
- Calculate the Test Statistic: Use sample data to compute the test statistic, such as the t-value or chi-square statistic, depending on the selected test.
- Make a Decision: Compare the calculated test statistic to the critical value or use the p-value to determine whether to reject the null hypothesis. If the p-value is less than α, reject H₀.
Interpreting Results and Drawing Conclusions
- Reject or Fail to Reject H₀: Based on your calculations, decide whether there is enough evidence to reject the null hypothesis or if you fail to reject it.
- Provide Context: Make sure to interpret the findings in the context of the research question. If you reject H₀, explain what that implies about the data.
- Consider the Limitations: Acknowledge any limitations or assumptions made during the process, such as sample size or distribution assumptions, that could affect the validity of the results.
By following these steps carefully, you can efficiently navigate through tasks that involve hypothesis testing, ensuring that your conclusions are well-supported by the data at hand.
Understanding Sampling Techniques for Assessments
In many assessments, you may be required to analyze a subset of data rather than the entire population. The process of selecting these subsets, or samples, is critical in ensuring the results are both reliable and valid. The right technique can lead to accurate conclusions, while an improper method may introduce bias or misrepresent the larger group. Understanding various sampling approaches and their proper applications is essential for interpreting and analyzing data effectively.
By choosing an appropriate sampling technique, you can ensure that the sample is representative of the population, which in turn enhances the credibility of the analysis and its outcomes. These techniques vary in complexity and are selected based on the context, available resources, and the nature of the population being studied.
Common Sampling Methods
- Simple Random Sampling: Every individual has an equal chance of being selected. This method ensures that the sample is free from bias and is representative of the population.
- Systematic Sampling: A sample is selected using a fixed interval, such as every 10th individual. This approach is often used when a list of participants or subjects is available.
- Stratified Sampling: The population is divided into distinct subgroups, or strata, and samples are taken from each. This method ensures that all segments of the population are well-represented.
- Cluster Sampling: The population is divided into clusters, and a random selection of clusters is chosen. Then, all members of the selected clusters are sampled. This method is often used when the population is large and dispersed.
When to Use Each Technique
- Simple Random Sampling: Ideal for smaller, homogeneous populations where each individual is equally likely to be chosen.
- Systematic Sampling: Works well when a population is organized in a list and there are no patterns that might influence the selection.
- Stratified Sampling: Best for heterogeneous populations where specific subgroups need to be analyzed separately to ensure representation.
- Cluster Sampling: Useful when working with large, geographically spread-out populations, where individual data collection may be impractical.
By mastering these techniques, you can ensure that your data is appropriately gathered and analyzed, leading to more accurate conclusions and a deeper understanding of the subject matter at hand.
Examining Common Statistical Distributions
In data analysis, understanding the behavior of data is crucial to making informed conclusions. Various types of distributions model how data points are spread across a population, and each distribution serves a unique purpose in representing different real-world scenarios. By recognizing the characteristics of these distributions, you can better analyze data patterns and make more accurate predictions.
Several commonly used distributions appear frequently in data analysis. These include distributions that describe how values are dispersed, how they cluster, and how they behave over time or space. Familiarity with these models helps in understanding the underlying trends and in making decisions based on probability theory.
| Distribution Type | Key Characteristics | Applications |
|---|---|---|
| Normal Distribution | Symmetrical, bell-shaped curve; mean = median = mode. | Widely used in natural and social sciences, such as human height and test scores. |
| Binomial Distribution | Discrete outcomes with two possible results; fixed number of trials. | Used in scenarios like coin flips or pass/fail tests. |
| Poisson Distribution | Describes the probability of a number of events occurring in a fixed interval of time. | Common in rare event modeling, such as phone call arrivals or system failures. |
| Exponential Distribution | Continuous probability distribution with a constant rate of occurrence. | Used in reliability testing, waiting times between events, etc. |
| Uniform Distribution | All outcomes are equally likely over a specified range. | Used in random number generation and situations where all outcomes are equally probable. |
Understanding when to apply each distribution helps streamline data analysis, enhance accuracy in predictions, and better interpret observed data patterns. Recognizing the conditions and assumptions behind each distribution type is key to effectively using them in practical situations.
Dealing with Complex Data Sets in Exams
Handling large or intricate data sets can be challenging, especially when you need to extract meaningful insights under time constraints. These data sets may contain a variety of variables, relationships, and potential patterns that require careful analysis. To manage such complexity, it’s essential to break down the data into manageable sections and apply appropriate techniques for interpretation.
One of the first steps in tackling complex data is organizing it effectively. Begin by identifying key variables and understanding their relationships. Look for trends, outliers, or unusual observations that could influence the overall analysis. This systematic approach allows you to focus on the most important aspects of the data, without getting overwhelmed by irrelevant details.
In cases where the data is large or multi-dimensional, using tools such as summarization techniques, visual aids, or statistical tests can simplify the analysis. These methods help condense the information into a form that’s easier to interpret, making it possible to draw accurate conclusions quickly.
Practice is crucial when dealing with complex data. Familiarity with common patterns and approaches will improve your ability to quickly identify the relevant techniques and apply them correctly during an assessment. Staying calm and methodical is key to handling challenging data sets effectively.
How to Tackle Multiple Choice Questions
Multiple choice assessments can often seem daunting, but with the right approach, they can be a straightforward part of the evaluation. These types of queries typically provide several possible solutions, making it essential to identify the most accurate one efficiently. Success relies on careful reading, logical elimination, and a strategic approach to decision-making.
The first step is to read each prompt thoroughly. Pay attention to the wording, as small details can significantly alter the meaning of the question. Ensure that you understand exactly what is being asked before looking at the answer choices.
Elimination Strategy

One of the most effective techniques for handling multiple options is elimination. Often, you can rule out one or two answers immediately if they are clearly incorrect. This narrows down your choices and increases the likelihood of selecting the right answer. If you’re unsure, consider the remaining options carefully and compare them to the question’s requirements.
Contextual Clues and Logical Reasoning
Sometimes, the right answer becomes apparent through context or logical reasoning. Look for clues in the question or even in other parts of the assessment that might guide your decision. If two answers seem similar, analyze the slight differences and determine which one better matches the criteria outlined in the prompt.
It’s also important to manage your time wisely. Don’t dwell too long on any one question. If you’re uncertain, make an educated guess and move on. This allows you to return to difficult questions later with a fresh perspective.
Using Real-World Examples in Statistics
Applying practical scenarios to mathematical concepts can significantly enhance understanding and problem-solving skills. By linking abstract theories to tangible examples, it becomes easier to visualize and interpret complex data. Real-world instances provide context, making seemingly difficult topics more relatable and easier to grasp.
For example, when analyzing trends in public health, real-world data on disease outbreaks can be used to illustrate how models are created and interpreted. This allows individuals to see how raw data is transformed into meaningful conclusions. Similarly, examining economic indicators such as inflation or unemployment rates provides insight into how statistical methods are applied in real-world decision-making.
Benefits of Real-World Examples
Using concrete examples offers several advantages:
- Enhanced engagement: Learners find it easier to connect with practical applications of theoretical concepts.
- Better retention: When concepts are tied to real-life situations, they become more memorable.
- Increased critical thinking: Analyzing real-world problems forces individuals to think critically about methods, assumptions, and outcomes.
How to Incorporate Examples Effectively

To make the most of these examples, choose those that are both relevant and understandable. For instance, using data from local surveys, sports statistics, or even everyday events like weather patterns can create powerful learning moments. The key is to align the example with the lesson’s goal while ensuring clarity and accessibility.
Incorporating real-world examples doesn’t only enhance comprehension, it also improves the ability to apply concepts in practical, everyday scenarios.
Revising Key Statistical Terms and Definitions
Mastering the fundamental concepts is essential for tackling complex problems effectively. A strong grasp of key terms not only enhances comprehension but also aids in applying methods accurately. Familiarity with core terminology provides the foundation necessary for solving any related task, making it easier to navigate through more advanced material.
When reviewing, it’s helpful to focus on terms that frequently appear in tasks and exercises. A clear understanding of their meanings ensures that interpretations are correct and logical, avoiding confusion during problem-solving. Revisiting these definitions will solidify your ability to identify and apply them in various contexts.
Essential Terms to Know
- Mean: The average of a set of values, calculated by summing all values and dividing by the number of observations.
- Median: The middle value in a sorted list of numbers, representing the central point of a data set.
- Mode: The most frequently occurring value in a data set.
- Variance: A measure of how much values in a data set differ from the mean, indicating the spread of data.
- Standard Deviation: The square root of variance, providing a measure of spread in the same units as the data.
Strategies for Effective Revision
- Flashcards: Use cards with terms on one side and definitions on the other to quiz yourself regularly.
- Practice Problems: Apply definitions in sample problems to strengthen understanding and retention.
- Group Study: Discuss terms with peers, explaining concepts in your own words to solidify your knowledge.
By revisiting and reinforcing key terms, you can approach any related challenges with confidence, knowing that you have a solid foundation in place to support your problem-solving skills.
Final Exam Preparation Strategies for Success

Achieving success in any assessment requires careful planning and structured revision. Focusing on effective techniques can significantly improve performance and build confidence. The key is to break down the material into manageable sections and approach it systematically, ensuring every important topic is covered thoroughly.
As the test day approaches, it’s crucial to develop a strategy that emphasizes both knowledge retention and time management. This involves not only reviewing content but also practicing with sample exercises and refining test-taking skills. Following a strategic approach will enable you to remain calm and organized when the time comes to demonstrate your understanding.
Effective Study Techniques
- Create a Study Schedule: Plan your revision ahead of time by dividing topics into smaller chunks and allocating specific time for each section. This ensures thorough coverage without feeling overwhelmed.
- Active Recall: Instead of passively reading notes, test yourself by recalling key points without looking at the material. This technique boosts long-term retention and identifies areas that need further focus.
- Teach What You’ve Learned: Explaining concepts to a peer or even to yourself reinforces your understanding and highlights any gaps in knowledge.
Strategies for Test Day
- Time Management: Start by quickly scanning through the test to get an overview. Allocate time to each section and stick to your plan to avoid spending too much time on any one part.
- Stay Calm: Maintain composure even if you encounter difficult tasks. If unsure, move on to the next and come back to it later with a clearer mindset.
- Double-Check Your Work: If time allows, review your answers to ensure they are complete and free from errors.
By using these preparation strategies, you can maximize your chances of success and approach the final assessment with confidence and clarity.