
Preparing for a comprehensive assessment in a technical subject requires a solid grasp of key concepts, as well as the ability to apply them effectively. Mastery of the core principles is crucial to solving problems and interpreting data accurately. This section aims to guide you through the process of understanding the essential topics, offering valuable insights to help you perform with confidence.
Focus on clarity and precision when reviewing key areas. By honing your understanding of fundamental methods and techniques, you’ll be equipped to tackle a wide range of problems. Confidence comes from consistent practice and a strong foundation, which will be essential when faced with challenging scenarios.
Essential Business Statistics Exam Concepts
To succeed in an assessment involving quantitative analysis, it is important to understand the core principles that underpin the subject. A strong foundation in key topics will ensure that you’re able to solve problems effectively, interpret results accurately, and approach each challenge with confidence. This section highlights the most critical concepts to focus on during your review process.
- Data Interpretation: Understanding how to read and analyze various forms of data is vital. Being able to quickly assess trends and draw meaningful conclusions will help in a wide range of tasks.
- Probability Theory: Knowing the likelihood of different outcomes is essential in decision-making processes. This concept forms the basis for many other analytical techniques.
- Measures of Central Tendency: Mean, median, and mode are fundamental to understanding how data is distributed and how to summarize large sets of numbers effectively.
- Dispersion and Variation: Concepts like range, variance, and standard deviation allow for a deeper understanding of how data spreads, helping you to assess consistency and reliability.
- Hypothesis Testing: This method is critical for evaluating assumptions and testing theories. Knowing when and how to apply tests like t-tests or chi-square tests is important for drawing accurate conclusions.
- Regression Analysis: Identifying relationships between variables and predicting future outcomes is a key skill in many fields. Regression analysis provides the tools to make informed predictions based on historical data.
By focusing on these concepts, you’ll gain a deeper understanding of the subject matter and be better equipped to handle the challenges that arise. Practice is key to mastering these techniques and applying them successfully in real-world scenarios.
Key Topics for Final Exam Preparation

When preparing for a comprehensive assessment in an analytical subject, it’s crucial to focus on the most significant areas that will be tested. These core topics form the foundation of the material, allowing you to apply your knowledge effectively and tackle complex challenges with ease. A targeted review of these essential concepts will help ensure you’re ready for any problem that may arise.
- Data Summarization Techniques: Mastering methods to summarize large data sets is crucial. Focus on central tendency measures like mean and median, along with dispersion metrics such as range and standard deviation.
- Sampling Methods: Understanding how to select representative samples and how sample size impacts the reliability of results is key. Familiarize yourself with techniques like random, stratified, and cluster sampling.
- Probability Fundamentals: Knowing how to calculate and interpret probabilities is essential. Pay attention to different probability distributions, including binomial and normal distributions.
- Hypothesis Evaluation: Be prepared to evaluate hypotheses through statistical tests. Understand the various testing methods such as t-tests and ANOVA, as well as how to interpret p-values and confidence intervals.
- Correlation and Regression: These concepts are vital for analyzing relationships between variables. Review how to calculate correlation coefficients and perform regression analysis to make predictions based on historical data.
- Statistical Inference: Knowing how to make inferences about a population from sample data is key. Study the principles behind estimation, confidence intervals, and the conditions required for valid conclusions.
By honing in on these core areas, you’ll gain the confidence to solve problems with precision and clarity. Consistent practice and understanding these vital topics will set you up for success during the assessment.
Understanding Descriptive Statistics for Business
In any field that involves data analysis, it’s essential to be able to summarize and interpret large amounts of information effectively. The ability to condense complex data into easily understandable insights allows for better decision-making and clearer communication. This section focuses on the key concepts that allow for the organization and description of data in a meaningful way.
One of the fundamental tools in this area is the use of central tendency measures, which include the mean, median, and mode. These values provide a single summary number that represents the center or typical value of a data set. Each measure has its strengths, and understanding when to use each one is essential for accurate analysis.
Another crucial concept is the concept of variation. Understanding how spread out the data is can reveal important insights. Measures like range, variance, and standard deviation help to assess this variability, allowing for more informed conclusions about data reliability and consistency.
Data visualization is also a powerful tool in summarizing information. Graphs like histograms, pie charts, and box plots allow you to see patterns, trends, and outliers at a glance, which can inform deeper analysis or highlight areas that need further investigation.
By mastering these techniques, you’ll gain a solid foundation for interpreting data in a meaningful way and using it to drive insights. Developing proficiency in these methods is key to confidently addressing more complex analytical challenges.
Mastering Probability and Its Applications

Probability is the cornerstone of making informed decisions when faced with uncertainty. By understanding the likelihood of various outcomes, you can analyze situations more effectively and predict future events with greater accuracy. This section focuses on key probability concepts that are fundamental to a wide range of analytical tasks.
Basic Probability Principles
At the heart of probability lies the concept of measuring uncertainty. Key ideas include calculating the probability of single events, understanding mutually exclusive and independent events, and using probability rules to solve problems. Mastering these basics is crucial for building a strong foundation for more complex analyses.
Applications in Real-World Scenarios
Probability has a wide array of practical applications, from risk assessment in finance to forecasting trends in marketing. Understanding how to apply probability concepts to real-world problems allows for better decision-making. By using techniques like conditional probability and Bayes’ Theorem, you can refine predictions and optimize strategies in various fields.
Becoming proficient in probability enables you to interpret data more effectively, predict trends, and make well-informed choices in uncertain situations. The ability to apply these principles to real-world challenges is an essential skill in many analytical fields.
Interpreting Data Distributions Effectively
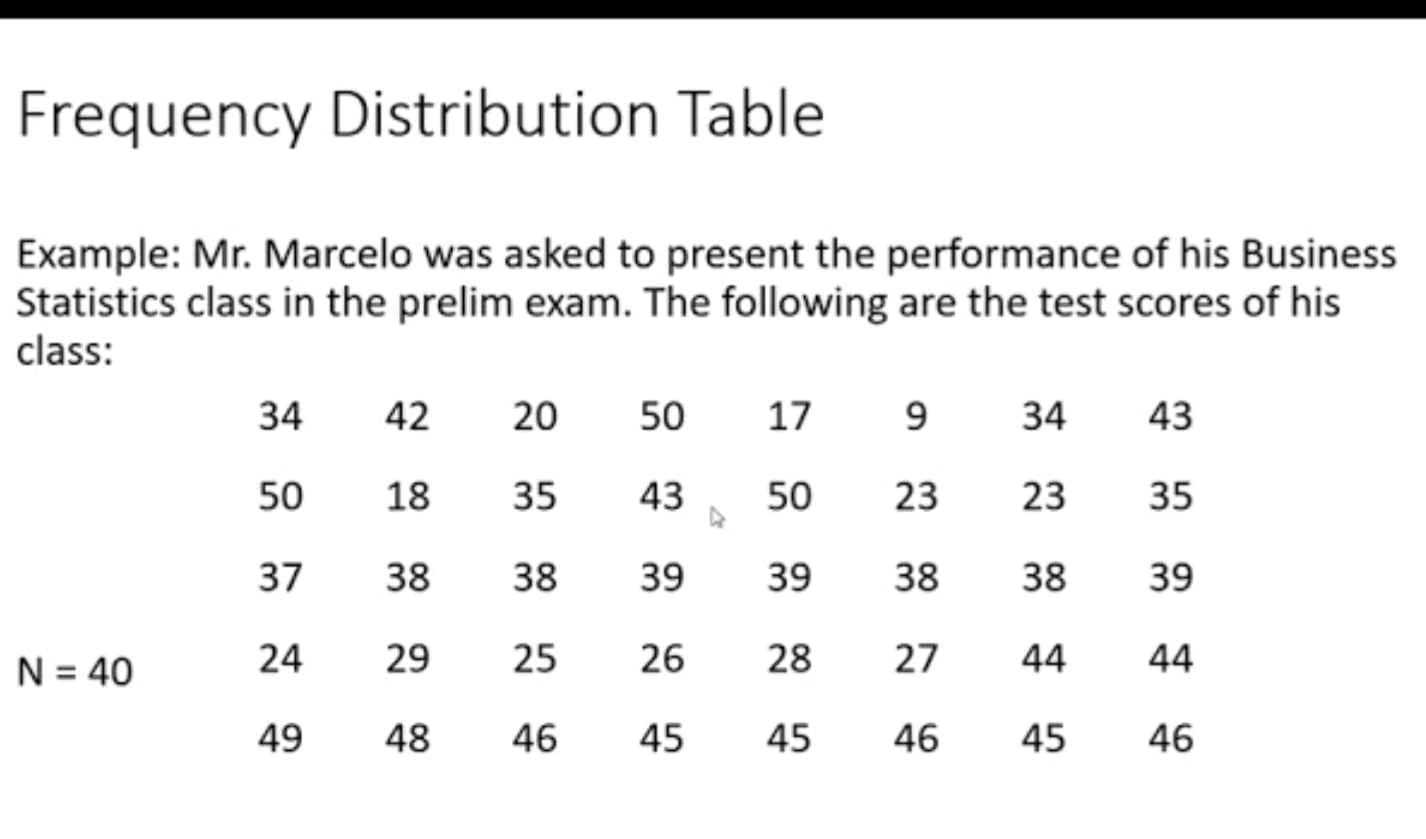
Understanding how data is spread across a range of values is a crucial aspect of data analysis. By interpreting distributions correctly, you can identify patterns, detect anomalies, and draw meaningful conclusions from large datasets. This section explores the key principles and tools needed to analyze distributions effectively.
- Shape of the Distribution: The first step in analyzing data distributions is recognizing their shape. Common patterns include normal (bell-shaped), skewed, and uniform distributions. Identifying the shape helps determine which analytical methods are most appropriate.
- Central Tendency and Spread: Measures like mean, median, and mode help identify the center of the distribution, while measures like range, variance, and standard deviation provide insight into the variability of the data.
- Outliers: Outliers are values that differ significantly from the rest of the data. Recognizing outliers is essential because they can indicate errors in the data or reveal unusual but important trends that need further investigation.
- Skewness: Skewness refers to the asymmetry of the distribution. Understanding whether a distribution is positively or negatively skewed can help in selecting the right analysis techniques and make interpretation more accurate.
- Kurtosis: This measure tells you about the “tailedness” of the distribution. A high kurtosis indicates heavy tails, meaning there may be more extreme values than expected, while low kurtosis suggests a more uniform spread.
By mastering these concepts, you can interpret data distributions with greater accuracy, leading to more effective analysis and decision-making. The ability to recognize key features in a distribution enhances your ability to draw reliable conclusions from data, making it a fundamental skill for anyone working with numbers.
Confidence Intervals and Their Use
When drawing conclusions from data, it’s often necessary to quantify the uncertainty associated with estimates. Confidence intervals provide a range of values that is likely to contain the true value of a parameter, offering a level of certainty about the precision of an estimate. This section will delve into the concept of confidence intervals and explore their practical applications.
- Definition and Purpose: A confidence interval gives an estimated range of values, derived from sample data, within which the true population parameter is expected to lie. The width of the interval reflects the level of uncertainty–wider intervals indicate greater uncertainty.
- Confidence Level: The confidence level, often expressed as a percentage (e.g., 95% or 99%), indicates the probability that the interval contains the true value. A higher confidence level results in a wider interval, but with greater certainty.
- Margin of Error: The margin of error is the range of values above and below the point estimate. It reflects the precision of the estimate and is influenced by sample size, variability, and confidence level.
- Practical Use in Decision-Making: Confidence intervals are widely used in decision-making processes, such as in market research or quality control. They help businesses assess risk, make predictions, and understand the reliability of data-driven conclusions.
- Interpreting Confidence Intervals: A common misunderstanding is to treat a confidence interval as a definitive range of possible outcomes. Instead, it represents the range within which the true value is likely to fall based on the given data.
By mastering the concept of confidence intervals, you can enhance your ability to make informed decisions based on data. Understanding how to calculate and interpret these intervals allows for more reliable conclusions, reducing the risk of error in estimates.
Analyzing Correlation and Regression

Understanding the relationships between variables is a critical aspect of data analysis. By identifying and quantifying these relationships, it’s possible to make informed predictions and gain deeper insights into underlying patterns. This section explores the concepts of correlation and regression, two fundamental tools for analyzing how variables are interconnected.
- Correlation: This concept measures the strength and direction of a linear relationship between two variables. A positive correlation indicates that as one variable increases, the other tends to increase as well, while a negative correlation means one variable decreases as the other increases.
- Correlation Coefficient: The correlation coefficient, often represented as “r,” quantifies the degree of linear relationship. Values range from -1 (perfect negative correlation) to +1 (perfect positive correlation), with 0 indicating no linear relationship.
- Types of Correlation: There are different types of correlation, including Pearson’s correlation for linear relationships, Spearman’s rank correlation for monotonic relationships, and Kendall’s tau for smaller data sets or ordinal data.
- Regression Analysis: Regression takes correlation a step further by modeling the relationship between variables and predicting one variable based on the other(s). It enables us to estimate values of a dependent variable based on known values of independent variables.
- Linear Regression: The simplest form of regression, linear regression seeks to fit a straight line to data points, providing a mathematical equation that best represents the relationship between the variables.
- Multiple Regression: This method extends linear regression by including more than one independent variable, allowing for the analysis of complex relationships involving multiple factors.
Both correlation and regression are essential for understanding how variables influence each other. Mastering these techniques allows for more precise predictions and informed decision-making, enabling analysts to draw reliable conclusions from data.
Important Hypothesis Testing Procedures

Hypothesis testing is a powerful method used to make data-driven decisions and assess the validity of assumptions. By systematically comparing data to a hypothesis, one can determine whether there is enough evidence to support or reject a claim. This section covers the core steps and methods involved in performing reliable hypothesis tests.
Setting Up the Hypotheses
The first step in hypothesis testing involves clearly defining two competing hypotheses. The null hypothesis (H₀) typically represents the status quo or no effect, while the alternative hypothesis (H₁) suggests that there is a significant effect or difference. The goal is to assess whether the evidence in the data is strong enough to reject the null hypothesis in favor of the alternative.
Choosing the Right Test
Once the hypotheses are defined, selecting the appropriate test is crucial for accurate results. Some common tests include:
- T-test: Used to compare the means of two groups, testing whether they are significantly different from each other.
- Chi-square test: Applied for categorical data to assess if there is a significant association between variables.
- ANOVA (Analysis of Variance): Used when comparing the means of three or more groups to see if at least one differs significantly from the others.
- Regression Analysis: Assesses the relationship between dependent and independent variables to test hypotheses about their interactions.
By carefully selecting the right test, analysts can draw valid conclusions and avoid common pitfalls such as Type I (false positive) and Type II (false negative) errors. These tests provide a solid foundation for making informed decisions based on empirical evidence.
Common Mistakes to Avoid in Exams
When it comes to assessments, even the most well-prepared candidates can make critical errors that impact their performance. Recognizing common pitfalls and taking steps to avoid them is essential for achieving success. This section highlights typical mistakes that can undermine your results and offers guidance on how to steer clear of them.
- Misunderstanding Instructions: Carefully read all instructions before starting. Skipping over or misinterpreting them can lead to answers that don’t align with what is being asked, ultimately costing valuable points.
- Not Managing Time Effectively: Failing to allocate time properly between questions often results in rushing through sections or leaving questions unanswered. Planning ahead and pacing yourself is key to finishing every part of the test.
- Overlooking Small Details: Small mistakes, such as miscalculating numbers or skipping units, can reduce the accuracy of your responses. Double-check your work to ensure all calculations and assumptions are correct.
- Answering Questions Out of Order: Jumping between questions without a logical approach can lead to confusion or overlooked items. Answer questions in a methodical order to avoid missing important steps or context.
- Relying Too Much on Memory: While memorization is important, relying solely on it can lead to errors when recalling complex concepts or formulas. Understand the underlying principles so you can apply knowledge flexibly.
Avoiding these common mistakes can help you perform more effectively, ensuring that your hard work pays off. With careful preparation and attention to detail, you can approach your assessments with confidence and clarity.
Preparing for Question Types in Exams
Each assessment comes with its own set of challenges, often structured around different types of inquiries that require various approaches. Knowing the format of questions in advance can help you prepare more effectively and respond with precision. This section outlines the common types of inquiries you might encounter and provides tips on how to tackle them with confidence.
- Multiple-Choice Questions: These questions assess your ability to recognize correct answers among a list of options. Focus on eliminating clearly incorrect choices and avoid second-guessing. Pay attention to wording, as it may provide subtle clues.
- Short-Answer Questions: These require concise, clear responses. Make sure to address the core points directly, without unnecessary elaboration. Stay focused on the specific aspect of the concept being asked.
- True/False Statements: These test your understanding of factual statements. Carefully analyze the statement before marking your answer. If you are unsure, look for keywords that could change the meaning of the statement.
- Problem-Solving Tasks: Often involving calculations or application of formulas, these questions assess your practical understanding of concepts. Always show your work step-by-step to ensure you capture all points for partial credit.
- Essay or Long-Form Responses: These questions require deeper analysis and a well-organized answer. Make sure to introduce your argument, provide supporting evidence or examples, and summarize your key points in a coherent structure.
By familiarizing yourself with these common question types, you can devise strategies for answering them effectively. Practice regularly, and don’t forget to review the key concepts that are most likely to appear in various forms during the assessment.
Time Management Tips for the Exam
Effective time management is crucial for success in any assessment. Properly allocating your time allows you to complete all sections thoroughly, reducing stress and maximizing performance. By adopting strategic techniques, you can ensure you have enough time for each part while avoiding the pressure of rushing through questions.
| Strategy | Description |
|---|---|
| Read Instructions Carefully | Take a few minutes to read the instructions thoroughly before starting. This will help avoid mistakes and ensure that you understand exactly what is expected in each section. |
| Allocate Time per Section | Divide your total available time according to the difficulty or length of each section. Plan to spend more time on sections that carry higher points or require more effort. |
| Start with Easier Sections | Begin with the questions that you find easier or more familiar. This will help you build confidence and ensure you don’t waste time on difficult questions in the beginning. |
| Time Yourself for Each Question | Set a time limit for each individual question to keep yourself on track. If you find yourself spending too long on one, move on and return to it later if time allows. |
| Leave Some Time for Review | Always save the last 5–10 minutes for reviewing your answers. Double-check your work for any mistakes or incomplete responses to maximize your score. |
By following these time management strategies, you can approach your assessment with greater focus and efficiency, ensuring that you make the most of every minute during the test.
How to Read and Interpret Charts
Charts are a powerful tool used to visually represent data, making it easier to identify patterns and trends. Being able to read and interpret charts correctly is essential for understanding the information they present. In this section, we will explore the key steps involved in analyzing visual data presentations and how to draw meaningful conclusions from them.
When approaching a chart, it is important to consider the following:
- Identify the type of chart: Different charts, such as bar graphs, line charts, or pie charts, are used to represent various types of data. Recognizing the chart type helps you understand how the data is organized and what to expect from the presentation.
- Understand the axes: In many charts, the x-axis and y-axis represent different variables. Make sure to review both axes carefully to understand what data each represents. For example, time may be represented on the x-axis, while the variable of interest is plotted on the y-axis.
- Examine the scale: The scale of the axes shows how the data is measured. Check the intervals and make sure you understand the range of values being presented. This will help you accurately assess the data points.
- Look for patterns: Once you understand the basic layout of the chart, look for trends, peaks, and dips in the data. Pay attention to any significant changes or correlations between variables.
- Consider the context: Always take into account the context of the data. Ask yourself what the chart is trying to convey, and ensure you are interpreting the information in light of the bigger picture or the question being asked.
By following these steps, you will be able to not only read but also interpret charts accurately, enabling you to make informed decisions based on the data presented.
Strategies for Solving Statistical Problems
Solving problems involving data analysis requires a clear and systematic approach. By employing effective strategies, you can simplify complex tasks and increase your chances of success. Whether you are working with probabilities, distributions, or regression, the right techniques can make a significant difference in your ability to understand and solve these challenges.
The following strategies can help guide you through problem-solving processes:
| Strategy | Description |
|---|---|
| Understand the Problem | Before jumping into calculations, take a moment to fully grasp what is being asked. Identify the variables involved and determine the type of problem you are dealing with. |
| Organize the Information | Write down the given data clearly. Having the information laid out in an orderly manner can help you identify patterns and make it easier to solve the problem. |
| Choose the Right Formula | Identify which formula or method is appropriate for the problem. Be sure to match the equation to the data type and the required solution. |
| Break Down the Problem | Complex problems can often be solved by breaking them into smaller, more manageable steps. Tackle each part of the problem one by one rather than attempting to solve everything at once. |
| Check for Logical Consistency | Ensure that your steps and calculations make sense as you go along. If something doesn’t seem right, retrace your steps to identify where the error may have occurred. |
| Double-Check Your Answer | After completing the problem, take a moment to review your final solution. Verify that your answer is reasonable and consistent with the context of the question. |
By following these strategies, you can approach data-related challenges with greater clarity and confidence, ultimately improving your ability to find accurate solutions to complex problems.
Understanding the Role of Sampling
Sampling plays a crucial role in data analysis by allowing researchers and analysts to make inferences about larger populations without needing to examine every individual. Instead of working with an entire set of data, which can be time-consuming and impractical, a smaller, representative sample is selected. This approach enables the extraction of meaningful insights while saving both time and resources.
By properly selecting a sample, you can make generalizations and predictions with a known level of uncertainty. The accuracy of these inferences depends largely on the quality of the sample chosen. A poorly chosen sample can lead to biased results, making it essential to use appropriate methods for selecting individuals or items that reflect the diversity of the whole group.
Key concepts related to sampling include:
- Random Sampling: This method ensures that every member of the population has an equal chance of being selected, reducing the risk of bias.
- Sampling Error: This refers to the difference between the sample result and the true population value, which can be minimized with larger or more representative samples.
- Sample Size: The larger the sample, the more accurately it reflects the population. However, larger samples also require more resources, so finding a balance is important.
- Stratified Sampling: Dividing the population into subgroups and sampling from each ensures that all important characteristics are represented in the sample.
Overall, understanding the role of sampling is vital for anyone involved in data-driven analysis. By selecting a representative sample and applying sound methods, you can draw valid conclusions and make informed decisions based on your findings.
Using Statistical Software for Analysis
In modern data analysis, specialized software plays a pivotal role in simplifying complex computations and enhancing the accuracy of results. By automating calculations, generating visualizations, and providing advanced modeling tools, these applications enable professionals to efficiently analyze large datasets and draw insightful conclusions.
With the power of statistical software, users can perform a wide range of tasks–from basic descriptive measures like averages and variances to more intricate analyses such as regression and hypothesis testing. The software’s ability to handle vast amounts of data without manual calculations greatly reduces human error and streamlines the process, making it an essential tool in various fields, including research, finance, healthcare, and marketing.
Key advantages of using statistical software include:
- Speed and Efficiency: Tasks that would take hours or days to compute manually can be completed in seconds, allowing analysts to focus on interpreting results.
- Advanced Functions: These tools offer capabilities for intricate analyses that are often difficult or impossible to perform manually, such as multivariate analysis or machine learning models.
- Visualizations: Most software provides built-in functions to create clear and informative charts, graphs, and tables, helping users understand the data and present findings effectively.
- Accuracy: By reducing the chances of human error, statistical programs ensure that calculations are precise, which is essential for reliable conclusions.
Whether you’re analyzing trends, testing theories, or predicting future outcomes, statistical software is a valuable resource that enhances both the quality and efficiency of your analysis. Understanding how to leverage these tools effectively is a key skill for anyone involved in data-driven decision-making.
Exam Questions on Business Forecasting
Understanding the techniques used for predicting future trends is essential for making informed decisions in any professional setting. To evaluate a deep understanding of forecasting methods, it’s crucial to test knowledge through various problems that challenge one’s ability to apply theoretical concepts to real-world scenarios. These problems may cover a wide range of topics, from simple moving averages to complex time-series models.
When preparing for an assessment in this area, it’s important to focus on both the mathematical foundations and the practical applications of these forecasting methods. Here are some typical areas that may be covered:
- Time-Series Analysis: Problems could involve analyzing historical data to predict future trends, using methods such as trend analysis, seasonal variations, and cyclical patterns.
- Regression Analysis: Expect questions that require you to use linear or multiple regression models to forecast values based on independent variables.
- Forecasting Errors: Analyzing the accuracy of forecasts and determining how to measure and minimize errors using techniques like mean squared error (MSE) or mean absolute percentage error (MAPE).
- Exponential Smoothing: Be prepared to apply this method to adjust predictions by giving more weight to recent observations.
- Qualitative Forecasting: Questions may require you to apply methods like expert judgment or market research when numerical data is scarce.
Each of these topics may be tested through problem-solving exercises where you need to compute, interpret, and explain your results. Being familiar with the tools and techniques used in forecasting, as well as practicing with real data, will help you confidently approach these types of tasks.
Key Formulas to Memorize for Exams

When preparing for an assessment in this field, having a strong grasp of the essential mathematical principles and formulas is critical. These formulas serve as the backbone of problem-solving, helping you quickly and accurately address a wide range of questions. Understanding when and how to apply each formula will allow you to navigate through complex problems with ease and confidence.
Here are some key formulas that are essential for effective problem-solving:
| Formula | Purpose |
|---|---|
| Mean (Average): (ΣX) / n | Used to calculate the central tendency of a data set. |
| Variance: Σ(Xi – μ)² / n | Measures the spread or dispersion of data points from the mean. |
| Standard Deviation: √Variance | Indicates the average amount of variation or dispersion of a set of values. |
| Linear Regression Equation: Y = a + bX | Used to predict a dependent variable based on the independent variable. |
| Correlation Coefficient (r): Σ(Xi – X̄)(Yi – Ȳ) / √Σ(Xi – X̄)² Σ(Yi – Ȳ)² | Measures the strength and direction of the relationship between two variables. |
| Exponential Smoothing: St = αXt + (1 – α)St-1 | Used for forecasting by smoothing data to predict future values. |
| Confidence Interval: CI = X̄ ± Z(σ/√n) | Estimates a range of values within which a population parameter lies, with a certain level of confidence. |
These formulas are essential for efficiently analyzing and interpreting data, helping you tackle problems in a systematic way. Memorizing these formulas, understanding their purpose, and practicing applying them to various scenarios will ensure that you are well-prepared for any challenges you encounter.
Tips for Reviewing Before the Exam

As the assessment approaches, it’s crucial to organize your study sessions effectively and focus on the most important material. A well-structured review strategy can help reinforce your understanding, identify any weak areas, and ensure you are fully prepared. By following some key techniques, you can maximize your review time and boost your confidence for the upcoming challenge.
Focus on Key Concepts
Concentrate on the core concepts that are most likely to appear in the assessment. Prioritize reviewing topics that you find more challenging, and make sure you understand the underlying principles. If you’re unsure about a particular area, go over practice problems or seek help to clarify your doubts.
Utilize Practice Problems
Working through practice problems is one of the most effective ways to prepare. These problems help you apply theoretical knowledge to real-life scenarios, improving your problem-solving skills. Try to simulate the test environment by setting time limits, which will help you manage your time during the actual assessment.
By using these strategies, you will not only reinforce your knowledge but also improve your ability to tackle different types of problems with ease. Make sure to stay focused, practice regularly, and maintain a positive mindset as you review.