
To excel in advanced mathematics, it is essential to strengthen your problem-solving skills through regular exercises and comprehensive reviews. Familiarity with the structure and content of assessments can make a significant difference in achieving a top score. Understanding key concepts and applying them effectively will ensure you approach challenges with confidence.
By engaging in exercises designed to reflect real test conditions, you can improve both your speed and accuracy. Focus on honing your critical thinking abilities and learning how to break down complex problems into manageable steps. This approach will allow you to tackle even the most difficult questions with ease.
Through consistent practice, you can gain a deeper understanding of mathematical principles and become more adept at solving a variety of problems. The more you expose yourself to different types of questions, the better prepared you will be to handle any situation on the day of the assessment.
Mastering the AP Calculus AB Exam
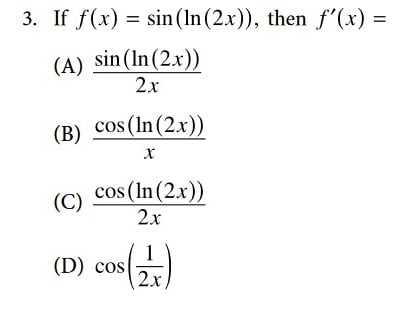
Achieving success in this challenging subject requires more than just memorizing formulas. It’s about developing a deep understanding of the material and honing the ability to apply mathematical concepts effectively under pressure. The journey toward mastering this assessment involves refining problem-solving techniques and building confidence in your abilities to tackle a wide range of mathematical problems.
Building a Strong Foundation

To truly excel, focus on the core principles that form the foundation of the subject. Ensure you are comfortable with key concepts such as limits, derivatives, and integrals. Having a solid grasp of these ideas will make it easier to approach more complex problems and understand their underlying patterns. The stronger your foundation, the easier it will be to connect various topics and apply them in different scenarios.
Sharpening Test-Taking Skills
Test preparation goes beyond just reviewing concepts. It’s also important to practice strategic time management and learn how to approach different types of questions efficiently. Develop the skill of quickly identifying the most effective methods for solving a problem, whether it’s through calculation, analysis, or approximation. By simulating real test conditions, you can build the endurance needed to stay focused and perform at your best when it matters most.
Essential Tips for AP Calculus Success
Achieving top performance in this subject requires a well-rounded approach that balances understanding key concepts, refining problem-solving skills, and managing time effectively. By following a few key strategies, you can enhance your readiness and boost your chances of success. Focus on consistency, clarity, and application in every aspect of your preparation.
Below are some essential tips that can help you maximize your potential and perform confidently during the assessment:
| Tip | Description |
|---|---|
| Understand the Core Concepts | Ensure you have a solid grasp of the fundamental principles, such as limits, derivatives, and integrals. These concepts form the backbone of the subject. |
| Develop Problem-Solving Skills | Focus on breaking down complex problems into smaller, manageable steps. This will help you approach each question with clarity and confidence. |
| Manage Your Time Effectively | During practice sessions, simulate real test conditions by timing yourself. This helps you build endurance and avoid time-related stress. |
| Work on a Variety of Problems | Exposing yourself to different types of questions helps you prepare for unexpected challenges and strengthens your adaptability. |
| Review Mistakes Thoroughly | Analyze errors to understand where your approach went wrong. This is crucial for learning and improving your problem-solving strategies. |
Key Topics to Focus On
To excel in this subject, it’s crucial to identify the most important concepts that will appear frequently and form the basis of many problems. By dedicating time to mastering these core areas, you can ensure a stronger performance on test day. Focus on understanding the principles behind each topic rather than memorizing formulas, as this will help you solve a wider range of problems effectively.
Limits and Continuity
Understanding limits is fundamental to many problems in advanced mathematics. It is essential to comprehend how functions behave near specific points and how this impacts their continuity. The concept of approaching a value, even when the function might not explicitly reach it, is central to many areas, including derivatives and integrals.
Derivatives and Their Applications
Derivatives represent the rate of change and are used to analyze the behavior of functions. Focus on the different rules for differentiation, such as the power rule, product rule, and chain rule. Additionally, understanding the applications of derivatives–such as optimization problems and motion analysis–will help you approach real-world scenarios efficiently.
Understanding AP Calculus AB Format

To approach this assessment successfully, it’s important to familiarize yourself with its structure and how it is divided. The format is designed to test your understanding of the material as well as your ability to apply concepts to different types of problems. Being aware of the layout will help you allocate your time more efficiently and approach each section strategically.
The assessment typically consists of two main sections: a multiple-choice part and a free-response segment. Each part evaluates different aspects of your mathematical knowledge and problem-solving abilities.
Multiple-Choice Section
- Time allocation: This section has a set number of questions that must be completed within a fixed time limit. Answering quickly and accurately is key.
- Content coverage: Questions cover a broad range of topics, including limits, derivatives, and integrals. Expect both conceptual and calculation-based queries.
- Answer strategies: Eliminate clearly incorrect options to improve your chances of selecting the right answer when uncertain.
Free-Response Section
- Problem-solving skills: These questions require a more in-depth approach. Be prepared to show all your steps and provide clear explanations for your solutions.
- Use of tools: Some questions may allow or even require the use of a calculator. Familiarize yourself with the tools permitted for this section.
- Time management: Allocate enough time to each question but leave room for reviewing your responses to avoid missing key details.
Effective Study Strategies for AP Exams
Success in any rigorous assessment requires a well-structured approach to preparation. To maximize your potential, it’s crucial to adopt strategies that not only enhance your understanding of key concepts but also optimize your performance during the test. A focused, methodical study plan can make all the difference when it comes to managing time and mastering the material.
Establish a Consistent Study Schedule
Consistency is essential when preparing for any challenge. Designate specific times each day for focused study sessions and stick to this routine as much as possible. Regular study intervals help reinforce learning and improve retention. Avoid cramming the night before–consistent, incremental learning is much more effective in the long term.
Utilize Active Learning Techniques
Engage actively with the material instead of passively reading or reviewing notes. Solve problems, summarize key points in your own words, and teach others what you’ve learned. These methods encourage a deeper understanding and ensure you’re truly grasping the material. Additionally, reviewing mistakes and analyzing why solutions work is a crucial part of mastering difficult topics.
Solving Practice Problems with Answers
Working through sample problems is one of the most effective ways to solidify your understanding of complex concepts and improve your ability to apply them under test conditions. By tackling a variety of problems, you not only reinforce your knowledge but also become more adept at solving different types of questions efficiently. Each problem offers an opportunity to enhance your skills and identify areas that need further attention.
Approaching Problems Step by Step
When solving problems, it’s important to follow a systematic approach to avoid errors and ensure accuracy. Break down each question into smaller parts and address them one by one. This methodical process allows you to focus on the details and apply the appropriate techniques effectively.
- Read the question carefully: Identify key information and determine what is being asked.
- Choose the right method: Decide on the appropriate mathematical principles or formulas to apply.
- Show all work: Writing out each step ensures clarity and helps prevent mistakes.
Learning from Solutions
After solving each problem, review the solution carefully. Pay attention to the methods used, as well as any shortcuts or alternative techniques that might make solving similar questions quicker in the future. Understanding why a particular approach works will deepen your comprehension and help you recognize patterns in future problems.
- Compare your steps: Check if your process matches the solution to identify any gaps in your approach.
- Understand the reasoning: Focus on how the solution was derived, not just the final result.
- Practice variations: Solve similar problems to reinforce your learning and build confidence.
Common Mistakes to Avoid in Calculus
While studying advanced mathematics, it’s easy to fall into certain traps that can hinder your progress and lead to incorrect solutions. Recognizing and avoiding these common errors is crucial to mastering the subject. Many mistakes stem from misunderstandings of fundamental concepts or rushing through steps without careful thought. By being aware of these pitfalls, you can develop more effective problem-solving habits and improve your performance.
One of the most frequent issues is failing to properly simplify expressions or misapplying rules. For instance, when working with functions, it’s essential to maintain the correct order of operations and apply the right methods at each stage. Additionally, overlooking small details–like signs or units–can lead to errors that are difficult to spot later on.
Another common mistake is not fully understanding the underlying principles behind each technique. Memorizing formulas without comprehension can result in applying them incorrectly or failing to see connections between different concepts. Developing a deeper understanding of the ‘why’ behind the process will help you avoid this trap.
How to Tackle Multiple Choice Questions
Multiple choice questions are a common feature in many assessments, offering a range of options from which to choose the correct answer. While they may seem straightforward, these questions often require a strategic approach to solve efficiently and accurately. Developing a method for tackling multiple choice problems can help you maximize your score and minimize errors.
The first step is to carefully read each question and all of the answer choices. Often, some options can be ruled out immediately, which can increase your chances of selecting the correct response. Eliminating clearly wrong answers first helps narrow down the possibilities and makes the remaining choices easier to evaluate.
Another useful strategy is to look for clues within the question that can guide your thinking. Keywords and mathematical terminology can give you hints about the correct method to apply or the likely answer. Additionally, make sure to double-check calculations or steps if you’re unsure, especially if one of the answers seems almost right but doesn’t quite fit the problem.
Improving Problem-Solving Speed
In any timed assessment, speed is just as important as accuracy. Being able to solve problems quickly and efficiently allows you to maximize your performance, especially when time is limited. However, rushing through questions without careful thought can lead to mistakes. The key to improving speed lies in practice, familiarity with the material, and developing effective problem-solving techniques.
First, practice regularly: The more you engage with a variety of problems, the more familiar you become with different question types and methods. This familiarity allows you to recognize patterns and apply the right techniques quickly, reducing the time spent on each problem.
Next, focus on time management: While it’s crucial to solve each problem thoroughly, it’s equally important to avoid getting stuck on one question for too long. Develop a sense of when to move on and return to more challenging problems later. This way, you ensure that you address every question and make efficient use of your time.
Finally, simplify your approach: Work on developing strategies to solve problems in fewer steps. This could involve memorizing key formulas, using shortcuts, or recognizing common techniques that apply to multiple problems. The more efficient your process, the quicker you’ll be able to solve each question.
Utilizing Free Response Questions for Practice

Free response questions are an excellent way to deepen your understanding of complex concepts and develop your ability to think critically. These open-ended problems challenge you to apply multiple skills and techniques to find a solution, offering a more comprehensive test of your knowledge. By consistently working through free response questions, you can strengthen both your problem-solving abilities and your ability to explain your reasoning clearly.
Benefits of Free Response Questions
Unlike multiple choice questions, which offer a set of options, free response questions require you to generate solutions independently. This type of question allows you to showcase your reasoning, step-by-step solutions, and the application of various concepts. The primary advantages of working with free response questions include:
- Deepening understanding: These questions require you to explain your thought process and apply knowledge in a more detailed manner.
- Improved problem-solving skills: By tackling these questions, you improve your ability to approach complex scenarios logically.
- Better time management: Practicing these problems helps you refine how you manage your time and avoid overcomplicating steps.
How to Maximize Your Practice with Free Response Questions
To get the most out of free response questions, follow a structured approach that includes understanding the question, organizing your work, and reviewing your solutions. Here are some strategies for effective practice:
- Read carefully: Understand what each question is asking and identify the steps needed to solve it.
- Break it down: Divide the problem into smaller, more manageable parts to avoid feeling overwhelmed.
- Show all work: Write out each step clearly and methodically, which will help you catch any mistakes and ensure accuracy.
- Review your answers: After solving a problem, compare your solution to the correct one and analyze any errors to improve your process.
Time Management During the Exam
Effective time management is essential when facing any timed assessment. Allocating your time wisely ensures that you can address all the questions without feeling rushed or overwhelmed. With a limited amount of time, it’s important to approach each problem strategically, balancing speed and accuracy to maximize your score.
One of the most important aspects of managing your time during an assessment is understanding the time constraints for each section. Before you begin, take a moment to quickly survey the entire set of questions, estimating how long you should spend on each one. This approach helps prevent spending too much time on any single problem and ensures you have time to address everything.
It’s also helpful to prioritize your work. Start with the questions that seem easiest or most familiar, which will build confidence and save time. For more challenging problems, use the process of elimination, make educated guesses if necessary, and move on if you’re stuck–returning to more difficult questions later when you have more time.
Why Practice Exams Are Crucial
Simulating real testing conditions by completing full-length tests is an essential part of any preparation strategy. These mock assessments offer valuable insights into your readiness and highlight areas that may need more attention. By taking these exercises seriously, you can enhance both your knowledge and your ability to manage time effectively under pressure.
One of the primary benefits of such tests is that they help you become familiar with the format and types of questions you will face. By regularly engaging in these activities, you learn to anticipate what’s coming and refine your problem-solving strategies. This familiarity reduces anxiety and builds confidence, as you know what to expect on the actual test day.
Additionally, completing these exercises allows you to track your progress over time. You can identify which topics you have mastered and which require further review. This targeted focus ensures that you spend your study time efficiently, improving your overall performance.
Resources for AP Calculus Preparation
Preparing for a challenging assessment requires a variety of tools and materials to support your learning. Whether you’re looking to reinforce your understanding of key concepts or to refine your test-taking strategies, there are numerous resources available to help you succeed. From textbooks to online platforms, having the right study materials can make a significant difference in your performance.
Many students find that using a combination of study guides, online tutorials, and interactive problem-solving platforms helps them master the material more efficiently. These resources offer step-by-step explanations and practical examples to ensure a thorough understanding of the content. In addition, using a variety of formats allows you to approach learning from different angles, keeping the process engaging and effective.
In addition to these traditional resources, you can also benefit from practice sets that mimic the conditions of the real test. These sets allow you to apply what you’ve learned in a timed setting, helping you to develop both accuracy and speed. Pairing practice problems with detailed solutions also helps reinforce your knowledge and correct any misconceptions.
Calculus AB Calculator Usage Tips
The calculator is an essential tool when tackling complex problems that require quick calculations or graphing. It can help you save valuable time, especially when working through intricate equations or visualizing functions. However, it’s crucial to use it effectively to ensure you’re maximizing its potential without relying on it too heavily.
Understanding the Functions: Familiarize yourself with the various functions of your calculator before using it during assessments. Knowing how to quickly access advanced features like graphing, finding derivatives, or solving integrals can significantly speed up your work. Practice these functions regularly to avoid confusion during high-pressure moments.
Use It to Check Work: After solving a problem by hand, use the calculator to verify your solution. This method helps you catch any small mistakes and reinforces your understanding of the problem. However, avoid relying solely on the calculator to do all the work for you–calculators are tools, not substitutes for learning the concepts.
Optimize for Speed: In timed assessments, efficient use of your calculator is key. Learn shortcuts for common tasks and develop a system to move quickly through the questions. Time spent fumbling with settings can cost you points, so practice using the calculator in mock situations to build speed and confidence.
Understanding Concepts Behind the Answers
To truly master any assessment, it is essential to go beyond merely memorizing solutions and understand the fundamental concepts that drive those solutions. This deeper comprehension ensures that you can apply your knowledge flexibly and tackle a variety of problem types. It’s not just about knowing the correct procedure, but about grasping why that procedure works and how it can be applied in different scenarios.
When you solve problems, always take time to reflect on the principles that led to the solution. This approach helps in recognizing patterns, avoiding errors, and reinforcing your understanding of core ideas. Focusing on the reasoning behind the steps makes learning more meaningful and applicable to future challenges.
Breakdown of Key Concepts

Here are some key areas to focus on to strengthen your understanding:
| Concept | Importance | Application |
|---|---|---|
| Limits | Essential for understanding continuity and rates of change | Solving problems related to approaching values and behaviors of functions |
| Derivatives | Key to understanding rates of change and tangents | Used to find slopes, maximums, minimums, and optimize solutions |
| Integrals | Critical for determining areas and accumulations | Applied in problems involving area under curves, displacement, and total quantities |
Linking Theory to Practice
Once you’ve identified the key concepts behind each problem, practice applying these principles to a variety of questions. This helps strengthen your problem-solving skills and deepens your ability to think critically about new challenges. The more you understand the reasoning behind each step, the better equipped you’ll be to handle unfamiliar scenarios during assessments.
Boosting Your Confidence Before Test Day
The key to performing well on any high-stakes assessment lies not just in knowledge, but also in confidence. Feeling assured in your abilities allows you to approach the test with a calm, focused mindset. Building confidence before the big day is an essential step in achieving success. This section will outline practical steps to help you feel ready and prepared when the time comes.
One of the most effective ways to boost self-assurance is through consistent preparation. The more familiar you are with the content and the format, the more confident you’ll feel. Practice is essential, but it’s also important to approach each study session with a positive and proactive attitude. Focusing on your progress, not just the end goal, can help you stay motivated and calm.
Strategies to Build Confidence
- Simulate the Real Test Environment: Take full-length practice sessions under timed conditions to get used to the pacing and pressure.
- Review Mistakes: Don’t just focus on what you got right. Understanding your errors and learning from them will reinforce your knowledge and improve your approach.
- Reinforce Key Concepts: Spend time reviewing fundamental principles and formulas. Mastering these will give you confidence when tackling complex questions.
- Positive Visualization: Take time to visualize yourself succeeding on test day. This mental exercise can reduce anxiety and enhance performance.
Mindset and Preparation
A positive mindset plays a huge role in your performance. Remind yourself that preparation is a process, and it’s okay not to know everything perfectly. It’s better to focus on gradual improvement and trust that your hard work will pay off. Confidence comes from both mental and physical readiness, so ensure that you are well-rested, hydrated, and relaxed before the test.
By using these techniques to build your confidence, you’ll be ready to approach the test with a calm and assured demeanor, maximizing your chances for success.