
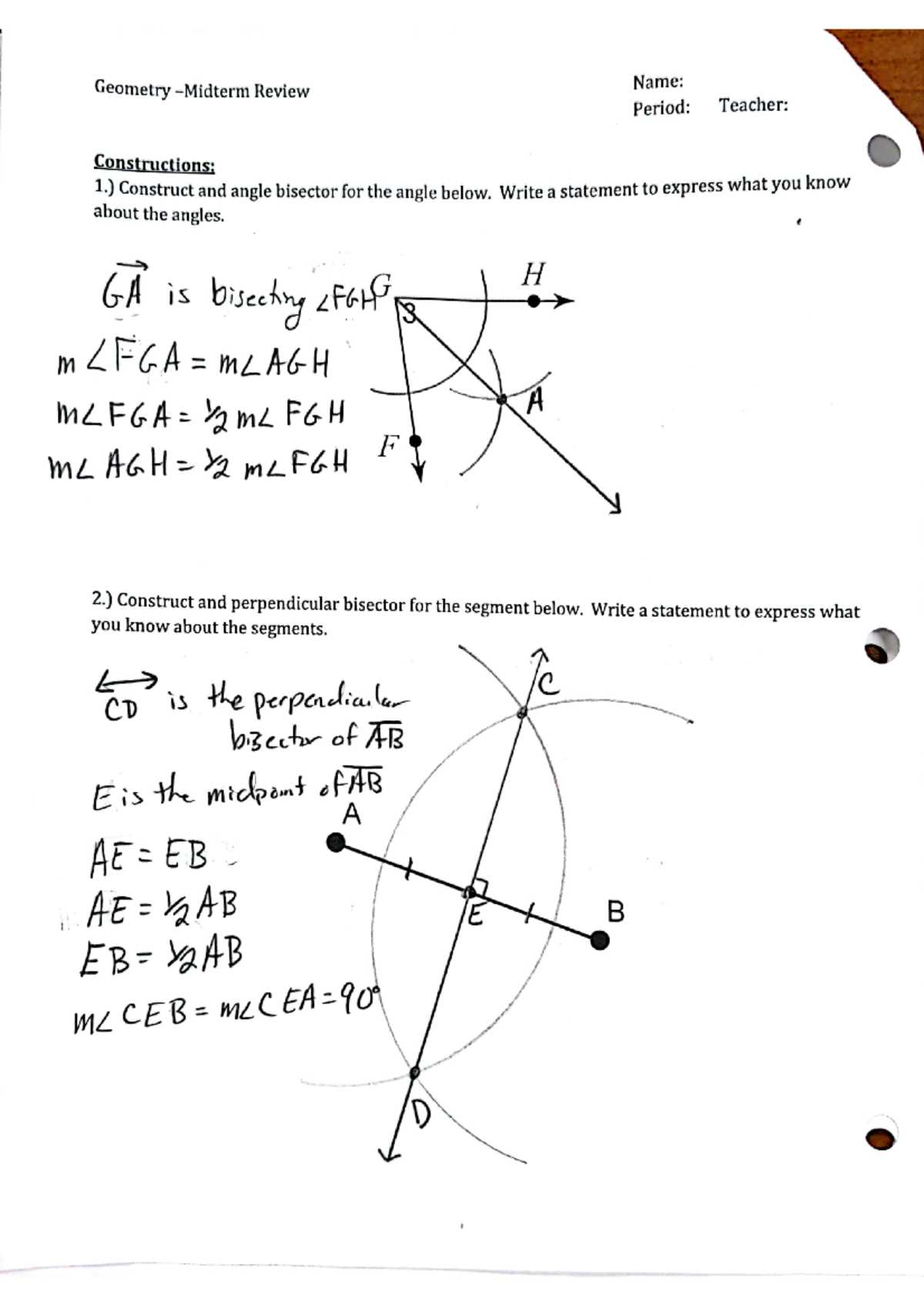
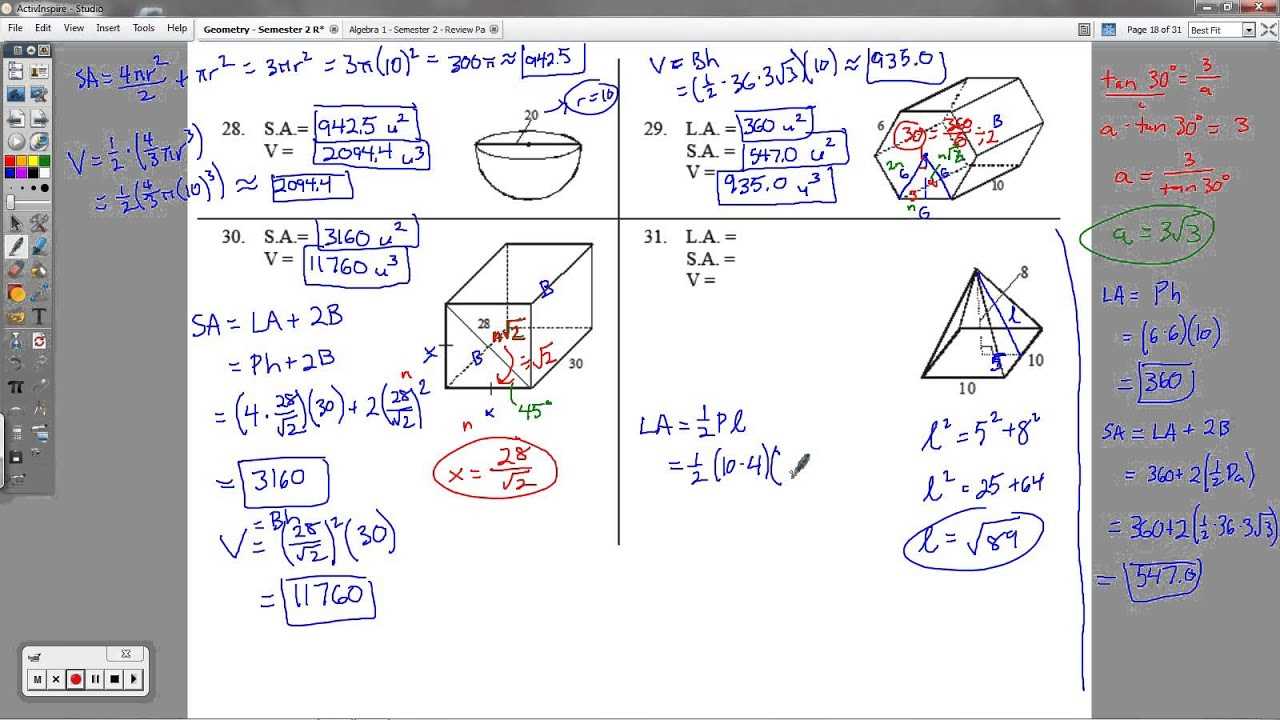
Preparing for a challenging test in mathematics requires a clear understanding of fundamental principles and an ability to apply them under time pressure. Whether you’re reviewing complex concepts or practicing specific problems, knowing how to approach the material is essential for success. This section aims to provide helpful insights for those looking to improve their problem-solving skills and perform well in their assessments.
Effective preparation involves more than simply memorizing formulas and theorems. It is about developing a deep comprehension of the logic behind each solution and being able to replicate that logic in various contexts. With the right strategies, students can increase their confidence and accuracy when tackling a wide range of problems.
In this guide, you’ll find detailed explanations of solutions, tips for avoiding common pitfalls, and practical advice for mastering key techniques. Whether you’re revising for a major assessment or refining your problem-solving strategies, these resources will help you achieve your goals and approach each question with confidence.
Mathematical Problem Solutions
This section provides detailed solutions to the most common types of problems encountered in an important assessment. By reviewing these solutions, students can gain a deeper understanding of the methodologies used to solve complex tasks and learn how to apply them in similar situations. The goal is to clarify any doubts and provide a step-by-step approach to solving challenging questions.
Each problem is explained with careful attention to the logical steps required for finding the correct results. By focusing on the underlying principles, this guide helps students not only find the right solutions but also grasp the reasoning behind each step. This approach ensures a stronger foundation for tackling future questions with confidence and accuracy.
Understanding the process is crucial for improving performance. The explanations provided here are designed to help reinforce key concepts, so you can approach future tasks with a solid grasp of the material. By breaking down each solution into manageable steps, students can see the structure of problem-solving and develop strategies for handling similar challenges on their own.
Additionally, the methodical nature of this guide encourages critical thinking and problem-solving skills that will be useful beyond any specific test or assignment. As you work through these solutions, you’ll be better equipped to handle both simple and complex problems in the future.
Overview of Important Mathematical Assessment
This section provides a general overview of the key components typically found in a significant mathematical evaluation. Such assessments are designed to test both theoretical understanding and practical application of core principles. By analyzing the structure and content of these tasks, students can better prepare and focus their study efforts on the areas that are most likely to appear.
Core Topics and Concepts
The evaluation often includes a variety of problems, from basic calculations to more complex scenarios involving proofs and reasoning. It covers a wide range of topics that challenge students to apply their knowledge in different contexts, ensuring a well-rounded demonstration of skills. Familiarity with these areas is essential for success, as it allows students to approach the test with confidence and efficiency.
Test Format and Time Management
Understanding the format of the assessment is equally important. These tasks usually consist of multiple sections, each focusing on different aspects of the subject. Time management becomes critical, as students must balance speed and accuracy to complete the assessment within the allotted time. Strategic preparation helps students allocate time appropriately for each section, ensuring they can tackle every question methodically.
How to Prepare for Mathematics Assessments
Effective preparation is the foundation for success in any major evaluation. To achieve the best possible results, it is crucial to develop a structured study plan that covers all the necessary topics while allowing ample time for practice. With the right strategies in place, students can approach the evaluation with confidence and clarity.
Start with a Review of Key Concepts
Focus on understanding the fundamental principles and formulas that are commonly tested. Make sure to review all essential theorems and practice applying them to various problems. This ensures you are well-prepared for any challenge that might arise during the assessment.
Practice Regularly
Consistent practice is key to mastering the material. Work through a variety of problems, starting with simpler tasks and gradually progressing to more complex ones. This helps reinforce your understanding and improves problem-solving skills, making you more comfortable when tackling similar questions in the assessment.
Focus on Problem-Solving Strategies
When preparing for the evaluation, it’s not only about memorizing formulas but also about refining your ability to solve problems logically and efficiently. Develop strategies for approaching different types of questions, such as breaking down complex problems into smaller steps and using diagrams where applicable.
Key Topics Covered in Mathematics Assessment
This section highlights the central themes typically tested in a significant mathematics evaluation. Understanding these fundamental concepts and areas of focus is crucial for effective preparation. Mastery of these topics ensures that students are equipped to tackle a wide range of problems with confidence and precision.
| Topic | Description |
|---|---|
| Shapes and Properties | Understanding the characteristics of different shapes, such as triangles, circles, and polygons, including their angles, sides, and symmetries. |
| Transformations | Learning about translations, rotations, reflections, and dilations, and how they affect the position and orientation of shapes. |
| Area and Perimeter | Calculating the area and perimeter of various geometric figures using appropriate formulas and methods. |
| Volume and Surface Area | Exploring the measurement of three-dimensional shapes, including cubes, spheres, and cylinders, to find their volume and surface area. |
| Angles and Parallelism | Working with different types of angles, such as acute, obtuse, and right angles, and understanding the properties of parallel lines and transversal intersections. |
| Pythagorean Theorem | Applying the Pythagorean theorem to solve problems involving right triangles and their sides. |
Understanding Mathematical Formulas for Assessments
Mastering essential formulas is a key aspect of preparing for any major evaluation in mathematics. These formulas provide the foundation for solving problems efficiently and accurately. It’s important not only to memorize them but also to understand the underlying concepts so that you can apply them in various scenarios.
Commonly Used Formulas
Below are some of the most frequently encountered formulas that are crucial for problem-solving:
- Area of a triangle: Area = 1/2 × base × height
- Area of a rectangle: Area = length × width
- Perimeter of a square: Perimeter = 4 × side
- Volume of a cube: Volume = side³
- Circumference of a circle: Circumference = 2 × π × radius
Applying Formulas Effectively
It’s important to practice applying these formulas in different contexts. Here are some tips to ensure you’re using them correctly:
- Understand the components: Break down the formula into its parts and make sure you understand the meaning of each element.
- Practice with varied problems: Work through different types of problems to become comfortable applying formulas in different situations.
- Double-check units: Always ensure that the units you use match the formula requirements (e.g., meters squared for area, meters cubed for volume).
By mastering these formulas and practicing their application, you can enhance your ability to solve problems quickly and accurately during any assessment.
Importance of Practice for Success
Consistent practice is one of the most effective ways to improve performance in any field of study. When it comes to mathematical subjects, regular practice allows students to become familiar with different problem types, sharpen their problem-solving skills, and build confidence in applying learned concepts. Without this practice, even well-understood principles can be difficult to recall under pressure.
Building Confidence through Repetition
By solving a variety of problems, students can strengthen their understanding and reduce anxiety during assessments. Repetition helps reinforce key concepts and familiarizes students with the structure of typical questions. As you work through problems, you not only improve your skills but also gain the confidence needed to approach new challenges with ease.
Improving Speed and Accuracy
When practiced regularly, problem-solving becomes more efficient. Familiarity with different techniques allows students to identify the most effective methods for solving problems quickly. By practicing under timed conditions, students can improve both their speed and accuracy, which are crucial for success in any challenging evaluation.
Common Mistakes in Mathematical Assessments
During important evaluations, students often make errors that could be easily avoided with a bit more attention to detail and careful preparation. These mistakes can range from simple miscalculations to more complex misunderstandings of fundamental concepts. Recognizing and understanding these common pitfalls can help students improve their performance and avoid costly errors on test day.
Misunderstanding Key Concepts
One frequent mistake occurs when students fail to fully understand the core principles behind the problems they are solving. Without a clear grasp of the concepts, it becomes easy to misapply formulas or overlook critical details. Focus on comprehension rather than memorization to ensure you’re applying the right approach to each question.
Rushing Through Calculations
Another common error is rushing through the calculation process, especially when students feel pressured by time. In their haste, they may overlook signs, miss steps, or make simple arithmetic mistakes. Double-checking each step can help prevent these careless errors and improve overall accuracy.
By identifying these common mistakes and working on strategies to avoid them, students can significantly improve their performance and tackle questions with greater confidence.
Steps to Solve Mathematical Problems Quickly
Speed and accuracy are essential when solving mathematical problems, especially under timed conditions. Developing a strategy for approaching each question can help you solve problems more efficiently, reducing the likelihood of errors and improving your overall performance. Below are a few proven steps to solve problems quickly and confidently.
1. Understand the Problem
Before jumping into solving, take a moment to read the problem carefully and understand what is being asked. Identify the key information and what you need to find. Clarifying the question in your mind helps avoid unnecessary confusion and ensures you focus on the relevant details.
2. Choose the Right Approach

Once you understand the problem, decide on the best strategy for solving it. Whether it’s applying a specific formula or breaking the problem into smaller parts, choosing the right approach is crucial. Stay calm and avoid overcomplicating the problem. A well-thought-out approach will save you time in the long run.
By following these steps and practicing regularly, you will become more efficient at solving problems quickly and accurately.
Mathematical Solutions and Explanations
This section provides detailed solutions and explanations for common mathematical problems. Understanding the steps involved in solving each type of problem is crucial for improving both accuracy and speed. By breaking down each solution, you can learn how to approach similar questions in the future with confidence and clarity.
Each solution will be followed by a clear, step-by-step explanation of the reasoning behind the steps taken. This method not only helps you arrive at the correct answer but also strengthens your understanding of the underlying concepts, enabling you to apply them in different scenarios.
Example 1: Solving for the Area of a Circle
To find the area of a circle, we use the formula: Area = π × radius². For example, if the radius is 5 units, the area would be:
Area = 3.14 × (5)² = 3.14 × 25 = 78.5 square units.
Understanding the logic behind this formula helps you apply it correctly in various situations, ensuring you achieve the desired results in tests or real-world applications.
Strategies for Time Management During Assessments
Effective time management is crucial when facing challenging assessments. Properly allocating time ensures that each section receives the attention it needs, reducing stress and maximizing performance. Developing a strategy for managing time during an evaluation helps you complete tasks efficiently while maintaining focus on accuracy.
Planning and Prioritizing
Start by reviewing the entire assessment and allocating time for each section based on its difficulty and point value. Prioritize questions you feel most confident about and tackle those first to gain momentum. This approach reduces the risk of spending too much time on challenging problems at the expense of easier ones.
Keeping Track of Time
During the assessment, regularly check the clock to ensure you are staying on track. If a question is taking longer than expected, consider moving on and returning to it later if time permits. It’s important to avoid getting stuck on a single question and losing valuable minutes.
Below is a sample time management breakdown for a typical assessment:
| Section | Time Allotted | Reasoning |
|---|---|---|
| Section 1: Easy Questions | 15 minutes | These are the quickest to answer and boost confidence. |
| Section 2: Moderate Difficulty | 30 minutes | Requires more focus but not as challenging as complex questions. |
| Section 3: Harder Problems | 45 minutes | These take the most time; ensure you have ample time to complete them. |
| Review Time | 10 minutes | Review the answers, ensuring accuracy and checking for missed questions. |
By following a structured time management plan, you can reduce pressure and stay focused, ensuring you complete the assessment efficiently and effectively.
How to Review Mathematical Concepts Effectively
Reviewing mathematical concepts effectively requires a structured approach that helps solidify understanding and improve recall. A focused review strategy not only reinforces key ideas but also enhances problem-solving skills, allowing you to approach each challenge with confidence. By using active review methods, you can ensure that you’re fully prepared for any assessment.
One of the most effective ways to review is by breaking down complex concepts into smaller, manageable parts. This allows you to focus on individual topics and ensures that no area is overlooked. Additionally, regular practice with a variety of problems helps reinforce your understanding and exposes you to different question types.
Below is a sample review strategy for mastering fundamental mathematical principles:
| Topic | Review Method | Recommended Time |
|---|---|---|
| Basic Formulas | Write out key formulas and practice using them in different problems. | 15 minutes |
| Shape Properties | Review properties of common shapes and their relations, such as angles and sides. | 20 minutes |
| Problem Solving | Work through various practice problems, focusing on those that challenge your skills. | 30 minutes |
| Review and Reflect | After solving problems, review your answers and reflect on any mistakes made. | 10 minutes |
By following this approach, you can focus your review sessions on the most important areas, gradually increasing your proficiency with each topic. A consistent and active review process will ensure that you retain key concepts and are prepared for any challenge.
Using Diagrams and Visuals in Mathematics
Visual aids, such as diagrams and charts, are powerful tools that can enhance understanding and simplify complex concepts. By representing problems visually, you can gain clearer insights into relationships, shapes, and calculations. These visuals serve as guides, making abstract concepts easier to grasp and apply in problem-solving scenarios.
The Importance of Visual Aids
In mathematics, many problems involve geometric shapes, spatial reasoning, and proportional relationships. By drawing diagrams, you can visually break down the problem into more manageable parts. This technique helps identify patterns, make connections between different pieces of information, and ensure accuracy in calculations.
How to Use Diagrams Effectively
- Sketch the Problem: Start by sketching the given information. Even rough diagrams can help organize your thoughts.
- Label Key Elements: Mark important points, lines, angles, and dimensions on the diagram to clarify what’s being asked.
- Use Color Coding: Different colors can help highlight different parts of the diagram, making it easier to differentiate various components.
- Draw to Scale: When possible, try to draw to scale to visualize distances and angles more accurately.
Common Visuals in Mathematics
Below is a list of common types of diagrams used in mathematical problem solving:
- Triangles (to analyze angles and side lengths)
- Circles (for radius, diameter, and sector calculations)
- Graphs (for analyzing relationships between variables)
- Vectors (to represent magnitude and direction)
Using diagrams and visuals not only helps you solve problems faster but also enhances retention, as visual representations often make the material more memorable. With practice, these tools can significantly improve your problem-solving strategies and accuracy.
Tips for Mathematical Test Success
Achieving success in any mathematical assessment requires a combination of preparation, strategy, and focus. A well-rounded approach can help you navigate challenges more effectively and perform at your best. By understanding key concepts, practicing regularly, and applying efficient problem-solving methods, you can significantly improve your chances of excelling.
Here are some useful strategies to enhance your performance and boost confidence during the test:
- Understand the Basics: Mastering foundational principles is essential. Ensure you have a clear understanding of essential formulas, properties, and theorems, as they often form the backbone of more complex problems.
- Practice Regularly: Consistent practice helps reinforce your skills and familiarize you with various question types. Work through sample problems and past tests to gain confidence and improve speed.
- Time Management: Manage your time wisely during the test. Allocate enough time for each section and avoid spending too long on a single question. If you get stuck, move on and return later if necessary.
- Read Carefully: Pay attention to every detail in the questions. Small mistakes often arise from misinterpreting the wording or missing crucial instructions.
- Stay Calm: Test anxiety can hinder your performance. Practice relaxation techniques, take deep breaths, and approach each question with a clear mind. A calm approach leads to better decision-making.
By following these tips, you can approach your mathematical assessments with greater confidence and increase your chances of achieving success. Remember, preparation and mindset play crucial roles in reaching your goals.
Importance of Showing Work in Mathematics
When solving mathematical problems, it’s crucial to document each step clearly and methodically. This practice not only ensures that you arrive at the correct solution, but it also allows for easier identification of mistakes. By showing your work, you demonstrate a structured approach to problem-solving and can track your reasoning throughout the process.
Benefits of Showing Work
There are several advantages to clearly writing down each step in your calculations:
- Clarity of Thought: Breaking down problems step by step helps you better understand the logic behind each solution, ensuring you don’t skip important concepts.
- Accuracy: By showing all intermediate steps, you can spot errors earlier and correct them before reaching the final answer.
- Helps Teachers and Graders: Teachers can assess your understanding of the problem-solving process. If a mistake is made, they can often award partial credit based on the work shown.
How to Effectively Show Work
When presenting your solution, make sure your steps are organized and easy to follow:
- Start with the given information and what is being asked.
- Write out all equations, formulas, and relevant theorems clearly.
- Ensure each step logically follows the previous one, with all calculations shown.
- Check your final solution and compare it to the steps taken to ensure everything aligns correctly.
In summary, showing your work is an essential practice in mathematics. It helps you stay organized, catch mistakes, and demonstrate your understanding of the problem-solving process. Whether working on assignments or assessments, taking the time to show every step can lead to greater accuracy and a deeper understanding of mathematical concepts.
How to Double-Check Your Mathematics Solutions
When solving mathematical problems, it’s important to review your work carefully to ensure the solutions are accurate. Double-checking allows you to catch errors, confirm the validity of your calculations, and increase your confidence in the final result. This process can help you identify common mistakes, such as miscalculations or misunderstood concepts, before submitting or finalizing your work.
Steps for Reviewing Your Work

To effectively double-check your solutions, follow these steps:
- Verify Given Information: Ensure you have the correct data before starting. Re-read the problem to confirm what’s being asked and what information is provided.
- Revisit Each Calculation: Go through each step of your solution process. Check whether all operations (addition, subtraction, multiplication, etc.) were performed correctly.
- Check Units and Labels: Ensure that you’re using the correct units and that they’re consistent throughout the problem. For example, make sure you’re working with square units when dealing with area or volume.
Additional Review Strategies
In addition to revisiting the steps, there are other strategies you can employ to double-check your results:
- Work Backwards: If possible, start with the final solution and work your way backward to check if all previous steps lead to the same conclusion.
- Use Different Methods: Try solving the same problem using an alternative approach or method. This can help you cross-verify the results and identify any inconsistencies.
- Compare with Examples: Compare your results with similar problems or solutions from textbooks or other sources to see if they align.
- Ask for a Second Opinion: If you’re unsure, discuss your solution with a peer or teacher to get feedback and confirm the correctness of your work.
In summary, double-checking your work is a vital step in ensuring the accuracy of your solutions. By following these strategies and taking time to carefully review your steps, you can increase your chances of identifying and correcting errors, leading to more reliable results.
Online Resources for Mathematics Help
In today’s digital age, there are numerous online tools and platforms that offer assistance with solving mathematical problems and preparing for tests. Whether you’re struggling with complex formulas or looking for step-by-step explanations, these resources provide valuable support to improve understanding and boost confidence. Online platforms offer a variety of materials, such as interactive tutorials, practice problems, and video lessons, making it easier for students to grasp challenging concepts.
Top Online Platforms for Mathematics Assistance
- Khan Academy: This free educational platform offers comprehensive lessons on a wide range of topics, including geometry and algebra. It features instructional videos, practice exercises, and personalized learning tools to help reinforce key concepts.
- Wolfram Alpha: Known as a powerful computational engine, Wolfram Alpha allows users to input equations and receive detailed step-by-step solutions, helping students understand the process of solving problems.
- Desmos: Desmos provides an interactive graphing calculator and other mathematical tools that are helpful for visualizing equations and geometric shapes. It is a great resource for understanding visual representations in math.
- Mathway: Mathway is a popular tool that solves problems from various branches of mathematics, offering instant solutions along with clear explanations for each step of the solution process.
Other Helpful Online Resources
- PatrickJMT: A YouTube channel offering thousands of video tutorials on various math topics. The content is clear and concise, helping students work through problems and understand key techniques.
- Brilliant: Brilliant offers interactive problem-solving courses focused on logical reasoning and critical thinking. It is ideal for students looking to deepen their understanding of mathematical concepts through engaging puzzles and challenges.
- Chegg Study: Chegg offers textbook solutions and homework help. Students can ask questions and get detailed answers from experts, providing an excellent way to ensure accuracy and improve learning.
- Coursera: Coursera partners with universities to provide high-quality online courses, including courses on math and science. Students can access video lectures, readings, and quizzes to reinforce their learning.
By leveraging these online resources, students can strengthen their understanding of mathematical concepts, clarify doubts, and improve their problem-solving skills. Whether for practice or direct help with assignments, these platforms provide flexible and accessible ways to excel in mathematics.
What to Do After the Mathematics Assessment
Once you have completed your mathematics assessment, the next steps are crucial for consolidating your learning and preparing for future challenges. It’s not just about waiting for your results; it’s an opportunity to reflect, review, and take proactive measures to improve your understanding and performance. Whether you feel confident or uncertain about your answers, the post-assessment period is key for growth and improvement.
Reflect on Your Performance
- Review Your Work: Take the time to go through the problems you solved, even if you felt confident during the test. Look for any mistakes or areas where you might have been unsure. This will help you identify any weaknesses to work on.
- Assess Time Management: Consider how well you managed your time during the test. Did you rush through certain sections or spend too much time on one problem? Understanding your pacing can help you improve for the next challenge.
- Stay Calm and Avoid Stress: It’s natural to feel anxious while waiting for results, but it’s important to stay positive. Focus on what you can learn from the experience rather than dwelling on mistakes.
Prepare for Future Success
- Identify Areas for Improvement: Review the sections where you struggled. Whether it’s specific concepts, formulas, or problem-solving techniques, make a list of areas that need more attention.
- Seek Additional Help if Needed: If you’re having trouble with certain concepts, consider reaching out to a tutor, using online resources, or discussing the material with classmates or instructors.
- Practice Regularly: Keep practicing similar problems regularly to reinforce your skills. Regular practice is key to mastery, especially when tackling complex subjects.
By taking these steps after your mathematics assessment, you not only reinforce what you’ve already learned but also set yourself up for future success. Reflection and targeted improvement are powerful tools that can help you achieve even better results in the future.