
When it comes to tackling an important test in a subject that requires analytical thinking and problem-solving, preparation is key. Understanding the core principles and applying them effectively can make all the difference in achieving a successful outcome. This guide aims to equip you with the strategies and insights needed to navigate your upcoming challenge with confidence.
From mastering essential mathematical techniques to refining your ability to interpret data, every aspect of the subject can be approached with the right mindset. By familiarizing yourself with common problem types and learning how to recognize patterns, you’ll be able to approach each question systematically. Practice, organization, and focus are essential components that will help you perform at your best.
Whether you’re revising complex concepts or working through sample problems, it’s important to stay calm and methodical. With the right preparation and a clear strategy, you’ll be well-equipped to demonstrate your skills and knowledge effectively.
Mastering Problem Solving Techniques
In any challenging assessment that involves mathematical reasoning and data analysis, the key to success lies in understanding the structure of the questions and applying the appropriate methods to solve them. By recognizing the types of problems you may encounter and practicing effective strategies, you can approach each task with confidence and precision.
Developing a Strong Foundation
Before diving into problem-solving, it’s essential to have a solid grasp of the fundamental concepts. This includes understanding the principles behind various calculations, such as distributions, probabilities, and hypothesis testing. The more familiar you are with these ideas, the easier it will be to quickly identify which approach to take during the assessment.
Approach Each Problem Systematically

Once you’ve identified the problem type, break it down into smaller, manageable steps. Start with what you know, then systematically work through the given information, checking your logic along the way. Attention to detail is crucial–misinterpreting even a small part of the question can lead to incorrect solutions. By maintaining a clear structure and checking your work, you increase your chances of success.
Understanding Key Concepts for Success

To excel in any assessment that involves mathematical reasoning and data interpretation, it’s essential to first understand the core principles that drive the subject. These foundational concepts serve as the building blocks for solving more complex problems and ensuring accuracy in your approach. With a clear grasp of these ideas, you can confidently tackle a wide range of challenges.
Fundamental Principles to Master
Start by focusing on the basic techniques that frequently appear in problems. These include essential operations like calculating averages, probabilities, and interpreting patterns in data. Mastery of these principles is vital for both simple and more advanced tasks.
| Concept | Importance |
|---|---|
| Data Distribution | Helps in understanding how data is spread and what trends to look for |
| Probability Calculations | Key to solving problems that involve uncertainty or likelihood |
| Hypothesis Testing | Allows you to assess whether assumptions are supported by evidence |
| Regression Analysis | Useful for predicting relationships between variables |
Applying Concepts in Practice
Once you’ve mastered the fundamentals, the next step is applying them in different scenarios. Practice with sample problems, and experiment with variations to strengthen your understanding. It’s important to recognize that mastery comes not just from memorizing concepts, but from actively using them to solve real-world problems.
Essential Formulas for Preparation
Mastering key formulas is crucial for tackling various problems in assessments that require numerical analysis. These formulas provide the foundation for solving different types of questions and ensure that you approach each task with the right tools at hand. Familiarity with these expressions can save valuable time and help you achieve accuracy in your solutions.
Core Formulas to Remember

Focus on the following essential formulas, which frequently appear in problems related to data analysis and mathematical reasoning:
- Mean (Average): The sum of all values divided by the number of values.
Formula: (Σx) / n - Standard Deviation: Measures the spread of values around the mean.
Formula: √(Σ(x – μ)² / n) - Variance: The square of the standard deviation.
Formula: Σ(x – μ)² / n - Probability: The likelihood of an event occurring.
Formula: P(E) = favorable outcomes / total outcomes - Linear Regression: Used for predicting values based on the relationship between variables.
Formula: y = mx + b - Binomial Distribution: Used for binary outcomes in a fixed number of trials.
Formula: P(x) = (nCx) * p^x * (1-p)^(n-x)
Why These Formulas Matter

Having these formulas at your fingertips allows you to quickly address problems involving averages, distributions, and probabilities. They are the building blocks for more complex calculations and are essential in providing structured, repeatable solutions. Regular practice with these formulas will help reinforce your understanding and boost your confidence when facing similar challenges.
Common Mistakes to Avoid During Assessments
When faced with an assessment that involves problem-solving and data analysis, it’s easy to fall into common traps that can affect your performance. Identifying and avoiding these mistakes can help you approach each question with more clarity and accuracy, leading to better results. Awareness of these pitfalls ensures that you stay on track and apply the right techniques to every task.
Failure to Read Questions Carefully
One of the most frequent mistakes is rushing through the questions without thoroughly understanding what is being asked. Often, key details are embedded in the wording, and missing them can lead to incorrect assumptions. Always take a moment to read each question carefully, paying attention to any specifics such as “round to the nearest whole number” or “show your work.”
Misinterpreting Data or Formulas

Another common issue is misinterpreting the given data or using the wrong formula for a problem. It’s easy to confuse similar-looking concepts or apply the wrong equation, especially under time pressure. Before solving, double-check that you are using the correct formula and that you understand the data’s meaning in the context of the question.
How to Interpret Statistical Data
Interpreting data is a crucial skill when analyzing numbers and drawing conclusions. It involves not only understanding the raw figures but also recognizing patterns, trends, and anomalies. The ability to accurately interpret data enables you to make informed decisions and derive meaningful insights from complex information.
Key Steps in Data Interpretation
Follow these steps to effectively interpret and understand the data in any context:
- Examine the Context: Understand where the data comes from and the purpose behind it. Knowing the source helps you assess its reliability and relevance.
- Identify Variables: Determine which variables are being measured and how they are related. Understanding these relationships is key to interpreting results accurately.
- Look for Trends: Identify any trends or patterns in the data. Are there consistent increases or decreases? Trends help you make predictions about future outcomes.
- Check for Outliers: Spot any data points that seem unusually high or low compared to the rest. Outliers can provide valuable insights but may also indicate errors or unusual occurrences.
Practical Tips for Data Interpretation
To strengthen your ability to interpret data, keep the following tips in mind:
- Always visualize data: Graphs and charts can make complex data easier to understand and highlight key patterns.
- Be cautious of biases: Ensure you’re not interpreting data based on assumptions or personal biases, as this can lead to misleading conclusions.
- Compare and contrast: Look at data from different perspectives and compare it with other sets to see if patterns hold across various sources.
Effective Time Management for Assessments
Efficient time management is essential when preparing for any assessment that requires careful thought and problem-solving. Properly allocating your time ensures that you can approach each section of the task methodically, without rushing or missing key details. By organizing your study sessions and assessment time wisely, you increase your chances of performing well under pressure.
Planning Your Study Sessions

Start by setting a clear study schedule well before the day of the assessment. Break your study time into manageable blocks, focusing on one topic or skill at a time. Prioritize areas where you feel less confident, but also make time to review concepts you already know to keep them fresh. The key is to balance both review and learning.
Time Management During the Task
When working through the assessment, keep track of time to ensure you’re not spending too long on any one question. If you encounter a particularly challenging problem, move on to the next one and return to it later if time permits. This strategy helps you cover more ground and prevents you from getting stuck on a single issue.
Mastering Probability and Distributions
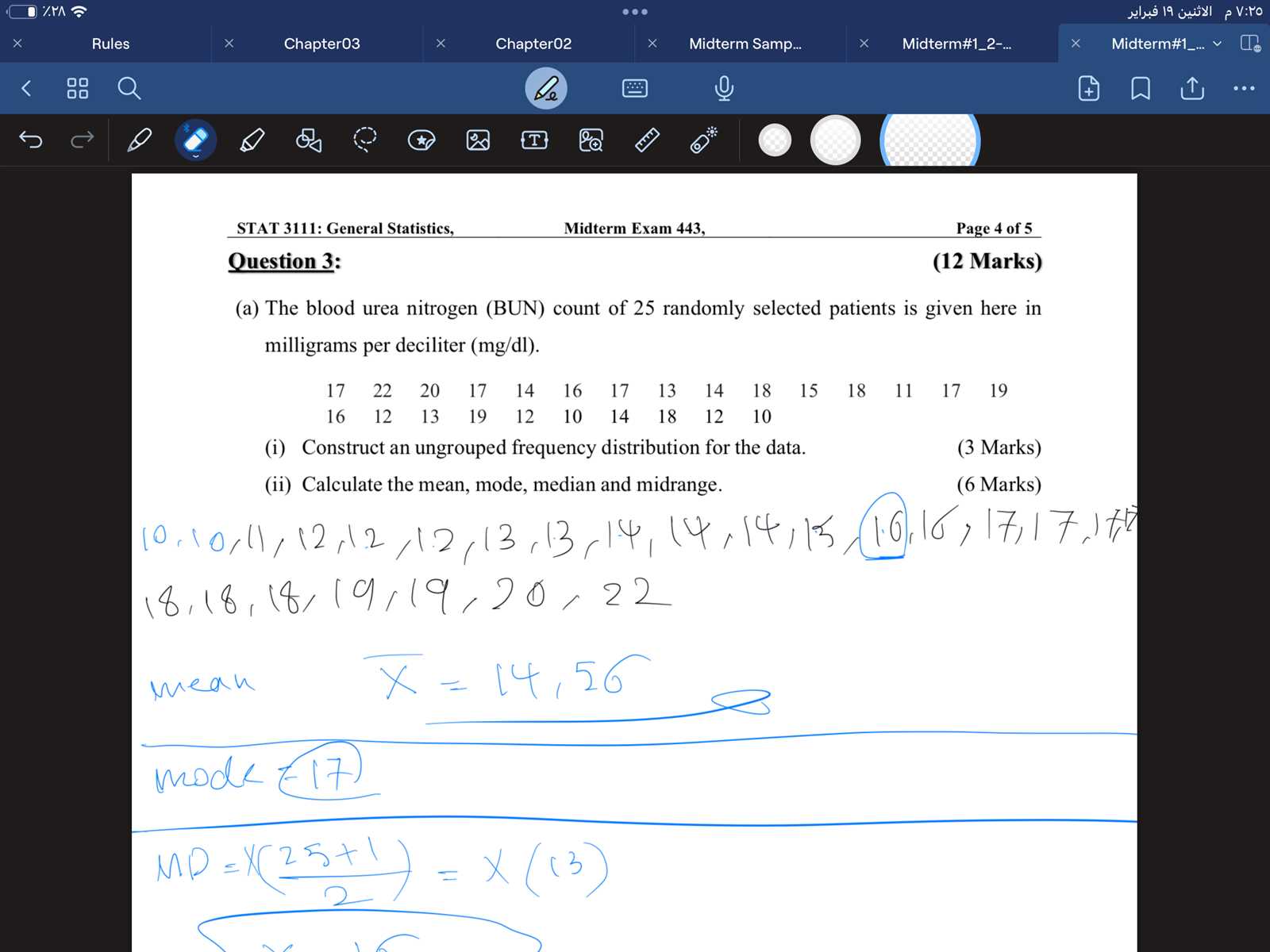
Understanding the concepts of probability and data distributions is essential for solving a wide range of problems involving uncertainty and prediction. These areas help you assess the likelihood of different outcomes and analyze how data points are spread across a given range. Mastery of these concepts allows you to interpret data more accurately and make informed predictions based on patterns and trends.
Key Concepts in Probability
Probability is the measure of how likely an event is to occur. To master probability, it’s important to become familiar with basic rules such as:
- Complementary Events: The probability of an event not happening is 1 minus the probability of it happening. P(A’) = 1 – P(A)
- Conditional Probability: The probability of an event occurring given that another event has already occurred. P(A|B) = P(A and B) / P(B)
- Independent Events: Events that do not affect each other’s probability. P(A and B) = P(A) * P(B)
Understanding Distributions
Distributions describe how data points are spread across a set of values. There are several types of distributions that are commonly used in analysis, such as:
- Normal Distribution: A bell-shaped curve where most of the data points cluster around the mean.
- Binomial Distribution: Used for binary outcomes (success or failure) over a fixed number of trials.
- Poisson Distribution: Represents the number of events occurring in a fixed interval of time or space.
By familiarizing yourself with these distributions and their properties, you can better assess probabilities and analyze data in a meaningful way.
Reviewing Hypothesis Testing Techniques
Hypothesis testing is a fundamental method used to make decisions or inferences about populations based on sample data. It involves formulating two competing hypotheses and using sample data to determine which hypothesis is more likely to be true. Mastering the techniques for hypothesis testing is essential for drawing valid conclusions from data and for making data-driven decisions.
Steps in Hypothesis Testing

The process of hypothesis testing generally follows these key steps:
- State the hypotheses: Formulate the null hypothesis (H₀), which represents the assumption that there is no effect or relationship, and the alternative hypothesis (H₁), which suggests that there is a significant effect or relationship.
- Choose the significance level: Select a significance level (α), commonly set at 0.05, which determines the threshold for rejecting the null hypothesis.
- Collect and analyze data: Gather sample data and perform the necessary calculations, such as calculating the test statistic.
- Make a decision: Compare the p-value to the significance level. If the p-value is less than α, reject the null hypothesis; otherwise, fail to reject it.
- Interpret the results: Draw conclusions based on the hypothesis test and discuss the implications of rejecting or failing to reject the null hypothesis.
Common Tests and Applications
Several common tests are used in hypothesis testing, depending on the type of data and the research question:
- Z-test: Used when the sample size is large and the population variance is known.
- T-test: Applied when the sample size is small, and the population variance is unknown. It compares the means of two groups.
- Chi-square test: Used to examine the association between categorical variables.
- ANOVA (Analysis of Variance): Compares the means of three or more groups to determine if there are significant differences.
By understanding and practicing these techniques, you can confidently apply hypothesis testing to a variety of scenarios, ensuring that your conclusions are based on sound statistical reasoning.
Using Graphs and Charts Efficiently
Visual representations of data, such as graphs and charts, are powerful tools for communicating complex information in a simple and digestible way. By transforming raw numbers into visual formats, these tools help highlight key patterns, trends, and outliers, making it easier to understand and interpret the data. However, to be effective, it’s important to choose the right type of graph or chart for the data you’re presenting.
Choosing the Right Graph or Chart
Different types of data require different visualizations. Below are some common graph types and their ideal uses:
- Bar Chart: Ideal for comparing discrete categories or groups. It is particularly useful when you want to show differences in magnitude between categories.
- Line Chart: Best for showing trends over time or continuous data. Use line charts to observe changes in a variable at regular intervals.
- Pie Chart: Useful for showing proportions of a whole. It is best used when you have a limited number of categories and want to display their relative sizes.
- Scatter Plot: Ideal for showing the relationship between two continuous variables. It helps to identify correlations or patterns in the data.
Tips for Effective Visualization
While selecting the appropriate chart is crucial, presenting it clearly is just as important. Here are some tips for effective data visualization:
- Label Clearly: Always provide clear labels for both axes and a title for the chart, so viewers can easily understand what the data represents.
- Use Colors Wisely: Use contrasting colors to differentiate between data sets or categories, but avoid overwhelming the viewer with too many colors.
- Keep It Simple: Avoid clutter. Only include elements that add value to the presentation of the data, and make sure the graph or chart is not too complex to interpret quickly.
By following these guidelines and choosing the right graph or chart for your data, you can make your findings more accessible and impactful to your audience.
Improving Analytical Thinking Skills
Enhancing your ability to analyze information critically is essential for making sound decisions based on data. Analytical thinking involves breaking down complex problems into simpler components, recognizing patterns, and drawing conclusions from evidence. Strengthening these skills helps you assess situations from multiple perspectives and find logical solutions to challenges.
To improve your analytical thinking, it’s important to practice several key approaches. First, always question assumptions and verify the facts before forming conclusions. Critical questioning allows you to avoid biases and ensure the data you’re using is reliable. Second, try to consider multiple explanations or outcomes, even if one seems more obvious. This broadens your understanding and helps avoid hasty judgments.
Another useful technique is to organize information logically. This could involve creating charts, diagrams, or outlines to visually map out relationships and trends within the data. Visualizing information makes it easier to identify connections that may not be immediately apparent. Finally, applying analytical thinking to real-world scenarios, through case studies or problem-solving exercises, reinforces your ability to think critically under various conditions.
By honing these practices, you can improve your ability to analyze information effectively, which will lead to better decision-making in both academic and professional settings.
Step-by-Step Guide to Solving Problems
Approaching problems in a structured, methodical way can greatly improve your ability to find solutions efficiently. Breaking down complex challenges into manageable steps helps ensure clarity and reduces the chances of making errors. This guide outlines a clear, step-by-step approach that can be applied to a variety of problem-solving scenarios.
Understanding the Problem
The first step in solving any problem is to fully understand what is being asked. Carefully read the problem statement, and make sure you identify the key information provided. Take note of any given data, what you are trying to find, and the relationships between different elements of the problem. If necessary, rephrase the problem in your own words to ensure clarity.
Developing a Plan
Once the problem is understood, the next step is to devise a plan for how to approach it. Think about the tools, methods, or techniques that could be useful for solving the problem. In some cases, you may need to use specific formulas or techniques, while in others, a more intuitive approach might be required. Outline the steps you will take to reach a solution and consider how each step connects to the next.
By following a clear, step-by-step process, you can tackle any problem with confidence. The more you practice this approach, the more natural it will become, helping you solve problems more efficiently and effectively over time.
Common Statistical Terms Explained Simply

Understanding key terms and concepts is essential for working with data and drawing meaningful conclusions. Some terms can seem complicated at first, but when broken down into simpler definitions, they become much easier to grasp. Here, we explain some of the most common terms used in data analysis in a straightforward manner.
| Term | Definition |
|---|---|
| Mean | The average of a set of numbers, calculated by adding all values together and dividing by the number of values. |
| Median | The middle value in a set of numbers when they are arranged in order from smallest to largest. If there is an even number of values, the median is the average of the two middle numbers. |
| Mode | The value that appears most frequently in a data set. |
| Variance | A measure of how spread out the numbers in a data set are. It is calculated by averaging the squared differences from the mean. |
| Standard Deviation | A measure of the amount of variation or dispersion in a data set. It is the square root of the variance. |
| Probability | The likelihood or chance of a particular event happening. It is expressed as a number between 0 and 1, where 0 means the event will not occur, and 1 means it will certainly occur. |
| Correlation | A statistical relationship between two variables. It indicates whether and how strongly pairs of variables are related. |
By familiarizing yourself with these terms, you’ll be better equipped to understand data and make more informed decisions. Remember, practice is key to mastering these concepts, so take the time to apply them in real-life scenarios for better understanding.
How to Read and Understand Exam Questions
Reading and understanding questions effectively is crucial for performing well in any type of assessment. Often, the ability to answer questions accurately depends not just on knowing the material, but also on interpreting the question correctly. This section focuses on strategies to help you read and comprehend questions more efficiently, ensuring you provide the best possible responses.
Breaking Down the Question
The first step in understanding any question is to break it down into manageable parts. Start by identifying the key components of the question. Pay attention to action words that indicate what the question is asking you to do, such as “explain,” “calculate,” “compare,” or “list.” These words can give you a clear idea of how to structure your answer.
Look for Important Details
Next, look for the essential details in the question. These might include specific numbers, conditions, or variables that will help guide your response. Often, questions are designed to test your ability to focus on the most relevant information, so being able to identify these key elements is critical.
| Action Word | Meaning |
|---|---|
| Explain | Provide a detailed description or reasoning behind a concept or process. |
| Calculate | Perform a mathematical operation or determine a value based on given information. |
| Compare | Identify similarities and differences between two or more items. |
| List | Provide a series of points or items in a clear, organized manner. |
| Summarize | Condense the main points of a topic into a brief overview. |
By following these strategies, you can ensure that you approach each question with a clear understanding of what is being asked. This will help you organize your thoughts and respond more effectively, improving your overall performance.
Practice Problems for Last-Minute Revision
When time is running out, focusing on practice problems can be one of the most effective ways to consolidate your understanding and boost your confidence. Solving problems allows you to apply concepts quickly, test your knowledge, and identify areas that need further attention. This section provides examples of problems that can help you sharpen your skills just before an important assessment.
Quick Review with Simple Problems
Start with simpler problems to refresh your memory. These are typically designed to help you recall basic principles and verify your understanding of fundamental concepts. Working through these problems quickly will also help you build confidence and improve your speed when faced with similar tasks in the future.
Challenging Problems to Test Skills
After practicing simpler problems, move on to more complex questions. These problems are often more challenging and require a deeper understanding of the material. They are great for testing your ability to apply multiple concepts at once and can help identify any gaps in your preparation.
Here are some example practice questions:
- Given a set of data, calculate the mean, median, and mode.
- Interpret a graphical representation of a dataset and identify trends.
- Using a provided formula, solve for a missing variable.
- Given two datasets, compare their distributions and identify key differences.
By working through these problems, you’ll be able to identify your strengths and weaknesses, ensuring you’re well-prepared when it’s time to apply your knowledge. The more problems you solve, the more confident and accurate you’ll become in your approach to similar questions.
How to Stay Calm During the Test

Feeling anxious or stressed before and during an important assessment is normal. However, managing these emotions effectively can significantly improve performance. Staying calm helps you think clearly, organize your thoughts, and make better decisions. In this section, we will explore techniques to remain composed and focused throughout the process.
Techniques to Manage Anxiety
Here are some practical strategies you can use to stay calm and avoid stress during the test:
- Deep Breathing: Focus on slow, deep breaths to help reduce tension and clear your mind.
- Positive Visualization: Imagine yourself successfully completing the tasks with ease. This can reduce negative thoughts.
- Break Down the Task: If the test feels overwhelming, break it into smaller, manageable sections. Tackle one section at a time.
- Stay Present: Focus on the current question instead of worrying about what’s coming next.
Pre-Test Preparation
Preparation before the test is key to building confidence and reducing anxiety. The more you know the material, the less likely you are to feel overwhelmed. Here are some tips to prepare effectively:
- Practice Under Time Constraints: Simulate test conditions by practicing within a set time frame to help you manage the clock on the real day.
- Get Enough Sleep: Resting well before the test ensures your mind stays sharp and ready to focus.
- Have a Healthy Snack: A light, nutritious snack can keep your energy levels up during the test, helping you stay alert.
By incorporating these techniques and preparing thoroughly, you’ll feel more confident and capable of staying calm under pressure, allowing you to perform your best when it matters most.
Tips for Retaining Statistical Knowledge
Retaining complex concepts and techniques can be challenging, especially when they are vast and require regular application. However, there are several strategies that can help reinforce the information you have learned, ensuring it stays with you in the long term. By employing active learning and consistent practice, you can strengthen your grasp on the material and enhance your ability to recall it when needed.
Active Learning Techniques
One of the most effective ways to retain information is through active engagement. Instead of passively reading or listening to lectures, try to apply what you’ve learned through problem-solving and real-world examples. Here are a few active learning strategies:
- Practice Regularly: Solving problems on a consistent basis helps solidify concepts and improves recall.
- Teach Someone Else: Explaining concepts to others reinforces your understanding and highlights areas that may need more attention.
- Create Visual Aids: Diagrams, charts, and mind maps can help visualize complex ideas and create lasting connections.
Effective Review Strategies
Reviewing material at regular intervals is crucial for retention. Repetition spaced over time enhances memory consolidation. Here are some techniques to help with this process:
- Spaced Repetition: Review material at increasing intervals to boost retention and avoid cramming.
- Self-Testing: Quiz yourself regularly to assess your understanding and identify gaps in knowledge.
- Use Flashcards: Flashcards are a great tool for quick reviews, particularly for definitions and key concepts.
By integrating these methods into your study routine, you can improve long-term retention and develop a deeper understanding of the material. Over time, this will allow you to apply your knowledge more effectively and confidently in any situation.
How to Review Results After the Test
Once the test is over, it’s important to take the time to review your responses and assess how well you performed. This process can provide valuable insights into your strengths and areas for improvement, helping you refine your approach for future assessments. Reflecting on your work allows you to better understand any mistakes and build a stronger foundation for future challenges.
Steps for Effective Review
To maximize the benefits of your review session, follow these structured steps to critically analyze your performance:
- Review the Questions: Start by reading through the test questions again, ensuring that you fully understand the context and requirements of each one.
- Compare Your Responses: Go through each of your answers and compare them with the correct solutions, paying close attention to any discrepancies.
- Identify Mistakes: Focus on the mistakes you made. Were they due to a misunderstanding of the question, a calculation error, or something else?
Analyzing Mistakes and Learning from Them
Simply identifying errors is not enough–it’s crucial to understand why they happened and how to avoid them in the future. Here are some strategies for improving after the review:
- Break Down Incorrect Answers: Look at each incorrect response and determine the root cause. Was there a gap in your knowledge, or was it a simple oversight?
- Practice Similar Problems: To strengthen areas where you struggled, practice similar questions to reinforce your understanding.
- Seek Feedback: If possible, ask for feedback from a teacher or tutor to gain a clearer understanding of where you went wrong.
By thoroughly reviewing your results, you can gain valuable insights into your test-taking habits and academic understanding. This reflection process will help you perform better in future assessments and ensure that you continue progressing in your studies.