
Understanding advanced mathematical topics can often be a challenge, but with the right resources, the learning process becomes more manageable. Tackling a variety of complex problems requires a solid grasp of core principles and the ability to apply them accurately. This guide provides a structured approach to improving your mathematical proficiency, focusing on solving common problem types effectively.
By breaking down each problem into simple steps, anyone can develop the necessary problem-solving strategies. With clear instructions and comprehensive explanations, mastering tricky equations and concepts becomes an achievable goal. Whether you’re reviewing for exams or strengthening your overall math foundation, this resource offers valuable insights for students seeking to enhance their understanding of key topics.
Glencoe Algebra 2 Skills Practice Answers
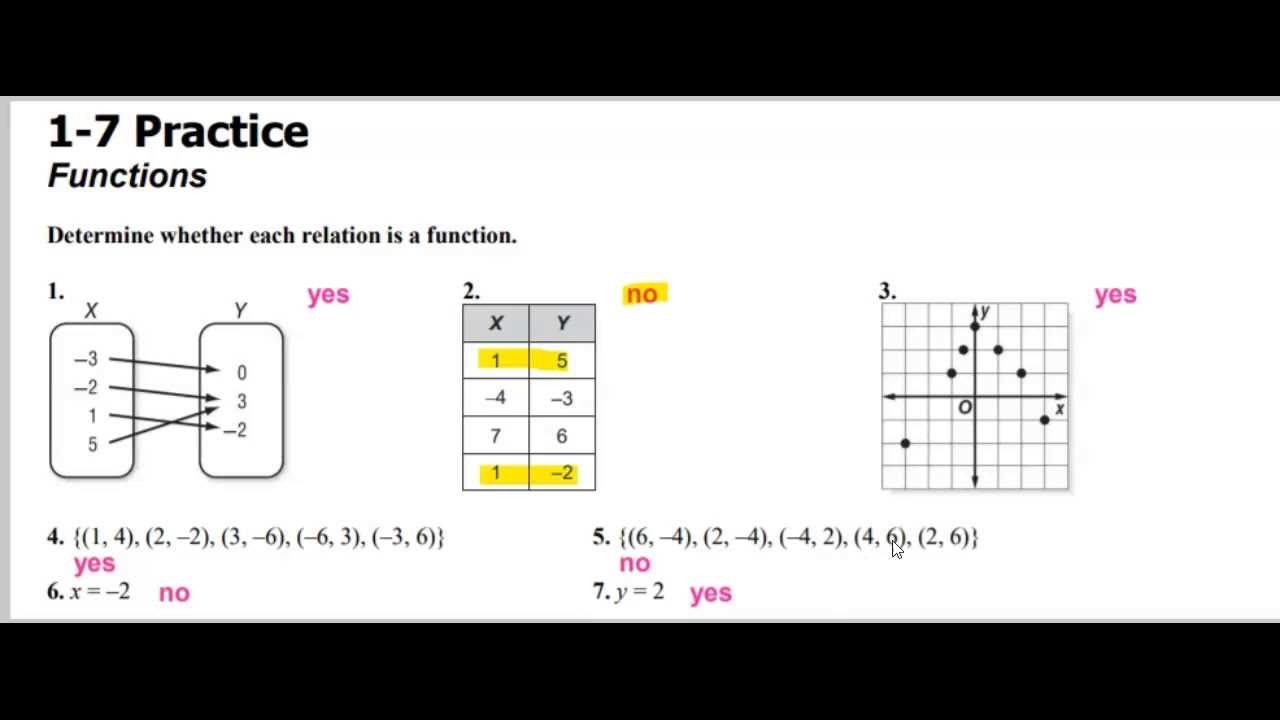
Mastering mathematical techniques requires consistent effort and a solid approach to solving various types of problems. With the right guidance, students can build a deep understanding of key mathematical concepts and apply them with confidence. This section provides solutions to common problems, breaking them down into manageable steps to help improve problem-solving abilities.
To excel in these exercises, it’s important to follow a systematic approach:
- Understand the core concepts behind each problem.
- Identify the necessary steps to solve it.
- Apply logical reasoning and perform calculations carefully.
- Review the solution to ensure accuracy and clarity.
For more complex problems, it’s crucial to break them into smaller, simpler components. This will allow you to focus on each part individually and avoid being overwhelmed by the overall task. With consistent practice, the ability to solve such problems will improve over time.
Here are some important strategies to keep in mind:
- Focus on fundamentals: Ensure a clear understanding of basic principles before tackling advanced problems.
- Check your work: Always review your calculations to avoid simple errors.
- Practice regularly: Repetition helps solidify your skills and boosts your confidence.
By following these tips and strategies, students will be able to solve a wide range of mathematical challenges and sharpen their problem-solving skills for more advanced topics.
Understanding the Practice Problems
To excel in advanced mathematics, it is essential to fully comprehend the problems at hand before attempting to solve them. Breaking down each problem into its core components allows for a better grasp of the underlying concepts and makes it easier to identify the right approach. This section will help you develop a structured method to interpret and tackle challenging exercises effectively.
Analyzing Problem Components

Each problem can be divided into smaller, manageable parts. Identifying these parts is the first step toward understanding the problem. Start by looking for key terms and identifying what the question is asking for. Once you have a clear understanding of the components, you can approach the problem logically and systematically.
Steps to Deconstruct Problems
Follow this simple strategy to break down problems for easier comprehension:
| Step | Action |
|---|---|
| 1 | Read the problem carefully and identify key terms. |
| 2 | Identify the type of operation or method needed (e.g., factoring, solving for x, etc.). |
| 3 | Write down any formulas or rules that may apply to the problem. |
| 4 | Break the problem into smaller, solvable parts. |
| 5 | Work through each part step by step to reach a final solution. |
By breaking the problem into logical steps, you will be able to identify the necessary tools and methods to reach a solution. Understanding the structure of each problem is key to solving it efficiently and correctly.
Key Concepts Covered in Algebra 2
Advanced mathematics introduces several essential principles that form the foundation for higher-level problem solving. Understanding these key ideas is crucial to building a strong mathematical framework. This section focuses on the core topics that are commonly explored, providing a clear overview of the concepts and techniques that are fundamental for success in this area of study.
One of the primary areas of focus is the manipulation of polynomials and rational expressions. These topics lay the groundwork for more complex operations and equations, which are essential for solving real-world problems. Additionally, the study of quadratic equations and their various forms provides critical insight into mathematical relationships.
Another important concept is the exploration of functions and their properties. Understanding how to interpret and work with different types of functions is necessary for tackling a variety of problems. This includes analyzing linear, quadratic, and exponential functions, as well as understanding their graphical representations.
Further, solving systems of equations and working with matrices are also integral to this level of study. These concepts help students develop problem-solving strategies that are applicable across a wide range of mathematical disciplines.
Mastering these key topics allows students to approach more challenging problems with confidence and precision, building a deeper understanding of how mathematical principles can be applied to real-world situations.
Step-by-Step Solutions for Practice Exercises
Solving mathematical problems effectively requires a structured approach. Breaking down each exercise into smaller steps helps students better understand the problem and arrive at the correct solution. This section outlines a clear, step-by-step method for tackling common types of problems, providing a systematic way to handle each challenge with confidence.
Breaking Down the Problem
The first step is to carefully analyze the given information. Look for key terms and identify what is being asked. By understanding the problem fully, you can determine the operations or methods needed to solve it. Start by simplifying the equation or expression, and eliminate any unnecessary components that might complicate the solution.
Applying the Right Techniques
Once the problem is broken down, apply the appropriate mathematical techniques. Whether you’re factoring expressions, solving for variables, or graphing equations, following a logical sequence is essential. Be sure to work through each step thoroughly, double-checking each calculation before moving on to the next phase.
By consistently using this step-by-step method, students will develop a stronger problem-solving ability and gain confidence in handling more complex exercises. Mastery of these basic techniques is crucial for success in more advanced mathematical topics.
Common Mistakes to Avoid in Algebra
Mathematical problems can be tricky, and even the smallest oversight can lead to incorrect solutions. Understanding common errors that occur during problem-solving can help prevent confusion and improve accuracy. This section highlights typical mistakes and provides tips on how to avoid them, ensuring a clearer and more efficient approach to solving exercises.
One common mistake is failing to properly distribute terms in expressions or equations. This often leads to incorrect simplifications and results. Another frequent error is neglecting to check for extraneous solutions when solving equations, especially when working with square roots or rational expressions. These solutions may appear valid at first glance but are often invalid once substituted back into the original equation.
Additionally, students often struggle with sign errors, such as incorrectly adding or subtracting negative numbers. It’s also important to be cautious with the order of operations, as applying them in the wrong sequence can completely alter the outcome of a problem. Taking the time to double-check calculations and carefully follow each step can significantly reduce these common mistakes.
Strategies for Solving Algebraic Equations
Solving mathematical equations requires a methodical approach to isolate the unknown variable. By following a set of effective strategies, you can simplify complex problems and solve them step by step. This section outlines key techniques that can help streamline the process, making it easier to find the correct solution.
One of the most important strategies is to first simplify both sides of the equation as much as possible. This can involve combining like terms, eliminating parentheses, and reducing fractions. Once simplified, the next step is to isolate the variable by performing inverse operations. For example, if the equation involves addition, subtract the same value from both sides; if it involves multiplication, divide both sides by the same number.
Working systematically is also essential. Always ensure that each step is clearly defined and follow a logical sequence. Checking your work after every step will help identify any errors early in the process. Additionally, when solving equations with multiple terms or variables, it’s important to keep track of all steps to avoid mistakes that might occur during the manipulation of the equation.
Lastly, remember that some equations may require more advanced techniques, such as factoring or using the quadratic formula. Understanding when to apply these methods is crucial to successfully solving more complex problems.
How to Interpret Algebra 2 Questions
Interpreting mathematical questions accurately is a critical first step in solving them correctly. Often, the phrasing of a problem can lead to confusion if not fully understood. By focusing on key terms and identifying the relationships between different parts of the equation, you can better navigate through complex problems and apply the right methods for solving them.
Start by carefully reading the question and identifying what is being asked. Look for any phrases that indicate specific operations or relationships, such as “find the value,” “solve for x,” or “simplify.” Pay attention to keywords like “sum,” “difference,” “product,” and “quotient” as they directly influence how the equation is structured. Understanding these terms ensures that you perform the correct operations in the right order.
Breaking down complex sentences is also crucial. If the problem is long or contains multiple steps, break it into smaller, more manageable parts. Rewriting the question in simpler terms can make it easier to understand what needs to be done. Always ask yourself: what do I know, and what do I need to find?
Contextual clues within word problems can provide additional information about the method you need to use. Identifying whether the problem involves a system of equations, a quadratic expression, or a rational function will guide your approach and allow you to select the right techniques for solving.
Tips for Efficient Problem Solving
Solving mathematical problems efficiently requires both strategy and practice. By adopting a methodical approach, you can avoid unnecessary steps and reach the correct solution more quickly. This section provides valuable tips to streamline your problem-solving process, ensuring that each step contributes meaningfully toward finding the answer.
One key tip is to always start by carefully analyzing the problem. Before jumping into calculations, take a moment to understand what the question is asking and identify the important variables or relationships. This will help you decide which technique or method to apply. The clearer your understanding, the more focused your approach will be.
Next, break down complex problems into smaller parts. By tackling one piece at a time, you make the process more manageable and less overwhelming. Don’t be afraid to simplify the problem or rewrite it in a more familiar form if that helps clarify your next steps. Efficiency comes from making the process logical and step-by-step.
Additionally, always check your work as you go. Performing quick spot checks after each step can help you catch any mistakes before they compound and lead to a wrong final answer. It’s also a good practice to use different methods when possible to verify your results, ensuring that your solution is correct.
Lastly, practice regularly. The more problems you solve, the faster and more efficient you become at recognizing patterns and applying the right techniques. With enough experience, problem-solving will become second nature, and you’ll be able to approach each question with confidence and clarity.
Mastering Polynomials in Algebra 2
Polynomials are a key topic in advanced mathematics, providing a foundation for solving more complex equations and understanding higher-level concepts. Mastering polynomials involves learning how to manipulate and simplify them effectively, as well as understanding their properties and how to solve equations that contain them. This section outlines the essential techniques for working with polynomials and developing a deeper understanding of their behavior.
One of the first steps in mastering polynomials is becoming familiar with their structure. Polynomials are made up of terms that include variables raised to different powers, with each term having a coefficient. Recognizing the degree of a polynomial and understanding how to classify its terms allows you to identify its form and structure, making it easier to work with in equations.
Next, learn how to perform operations on polynomials. Addition and subtraction of polynomials involve combining like terms, while multiplication requires using the distributive property (or FOIL method for binomials). Division, on the other hand, can be handled through long division or synthetic division, depending on the complexity of the problem.
Factoring is another critical skill when dealing with polynomials. Factoring allows you to break down complex expressions into simpler components, making it easier to solve equations and find roots. Understanding common factoring techniques, such as factoring by grouping, using the difference of squares, or applying the quadratic formula, is essential for solving polynomial equations effectively.
By practicing these techniques and familiarizing yourself with the different forms of polynomials, you’ll develop a solid understanding that will serve as a foundation for solving more challenging problems. Mastery of polynomials will also enhance your ability to approach higher-level topics, such as rational expressions and functions.
Factoring Techniques in Algebra 2
Factoring is an essential tool for simplifying mathematical expressions and solving equations. Mastering different factoring techniques enables you to break down complex expressions into simpler parts, making it easier to solve for unknown values or simplify complicated problems. This section covers various methods for factoring expressions, highlighting their uses and providing examples for better understanding.
Common Factoring Methods
There are several factoring methods that can be applied depending on the structure of the expression. Here are the most common ones:
- Factoring by GCF (Greatest Common Factor): Identify the largest factor that can divide all terms in the expression and factor it out. This method is the first step before applying other techniques.
- Factoring Trinomials: When dealing with quadratic trinomials, look for two numbers that multiply to give the constant term and add to give the middle coefficient. This method is especially useful for factoring expressions like x² + 5x + 6.
- Difference of Squares: If an expression follows the pattern of a² – b², it can be factored into (a + b)(a – b). This method is applicable when you encounter expressions involving squares.
- Perfect Square Trinomials: If an expression is a perfect square trinomial, it can be factored as (a + b)² or (a – b)². This applies when the first and last terms are perfect squares, and the middle term is twice the product of their square roots.
- Factoring by Grouping: For polynomials with four terms, grouping involves pairing the terms in a way that allows common factors to emerge. This technique can often simplify the expression and lead to a factored form.
Steps for Successful Factoring
To factor expressions effectively, follow these steps:
- Look for a GCF: Always begin by factoring out the greatest common factor from all terms in the expression. This simplifies the problem significantly.
- Identify the correct method: Depending on the structure of the polynomial, decide whether to use methods like factoring trinomials, difference of squares, or grouping.
- Check for factorization errors: After factoring, verify the result by expanding the factored form to ensure it matches the original expression.
- Practice regularly: The more you practice factoring, the easier it becomes to identify which method to apply and to solve problems more efficiently.
By mastering these factoring techniques, you can simplify complex problems and efficiently solve a wide range of equations. Each method has its own set of applications, so understanding when and how to use them is essential for success in solving mathematical expressions.
Solving Quadratic Equations Simplified
Quadratic equations often appear in many areas of mathematics, and solving them is an essential skill for tackling more advanced topics. These equations typically involve a variable raised to the second power, and finding their solutions can sometimes be tricky. However, with the right techniques and understanding, solving them can be a straightforward process. This section breaks down the methods for solving quadratic equations and offers tips for simplifying the approach.
There are several ways to solve quadratic equations, and each method is useful depending on the form of the equation. The most common methods include factoring, completing the square, and using the quadratic formula. By becoming familiar with these techniques, you’ll be able to choose the most efficient method based on the given equation.
Factoring is one of the simplest and most intuitive methods. If the quadratic equation can be factored into two binomials, you can solve it by setting each factor equal to zero. This method works well when the equation has integer solutions and can be factored easily.
Completing the square is another technique that allows you to solve any quadratic equation. It involves rearranging the equation so that the left side forms a perfect square trinomial. From there, you can solve for the variable by taking the square root of both sides. This method is particularly useful when the equation cannot be factored easily.
The most versatile approach is using the quadratic formula, which can solve any quadratic equation, regardless of whether it factors easily. The formula is:
x = (-b ± √(b² – 4ac)) / 2a
This formula gives two possible solutions for the variable, depending on the value inside the square root (the discriminant). If the discriminant is positive, the equation has two real solutions. If it’s zero, there is exactly one real solution. If it’s negative, there are no real solutions in the real number system.
By mastering these methods, you’ll be able to approach quadratic equations with confidence, whether you need to solve simple problems or tackle more complex ones. The key to success is recognizing the structure of the equation and applying the appropriate technique for the most efficient solution.
Understanding Rational Expressions
Rational expressions are mathematical expressions that involve fractions with polynomials in both the numerator and the denominator. These expressions are common in higher mathematics and require careful manipulation to simplify or solve. Understanding the structure and properties of rational expressions is essential for solving problems involving fractions and polynomials.
In essence, a rational expression is similar to a fraction, but instead of constants or numbers, it contains polynomials. Just like fractions, rational expressions can be simplified, added, subtracted, multiplied, or divided. Mastering the techniques to handle these expressions is key to solving more complex equations and problems.
Key Components of Rational Expressions
Rational expressions typically consist of the following elements:
- Numerator: The polynomial in the top part of the fraction.
- Denominator: The polynomial in the bottom part of the fraction.
- Restrictions: Values that make the denominator zero are not allowed, as division by zero is undefined. These values must be excluded from the solution set.
Simplifying Rational Expressions
Simplifying rational expressions involves reducing the fraction by factoring both the numerator and the denominator, then canceling out common factors. Here’s a step-by-step process:
- Factor both the numerator and the denominator, if possible.
- Cancel any common factors between the numerator and the denominator.
- Check the restrictions by identifying values that would make the denominator zero.
For example, consider the rational expression (x² – 9) / (x² – 6x + 9). To simplify it:
- Factor the numerator: (x² – 9) = (x – 3)(x + 3).
- Factor the denominator: (x² – 6x + 9) = (x – 3)².
- Cancel the common factor of (x – 3).
- The simplified expression is (x + 3) / (x – 3).
Understanding the process of simplifying rational expressions ensures that you can handle more complicated problems involving fractions with polynomials. Whether dealing with equations or simplifying individual terms, the key is recognizing factors and applying algebraic rules consistently.
Analyzing Functions and Graphs
Understanding how to interpret and analyze functions and their corresponding graphs is a fundamental skill in mathematics. By studying the relationship between input values and output results, you can identify key features of a function, such as its domain, range, and behavior. The graph of a function visually represents this relationship and provides valuable insights into its properties.
In this section, we will explore the essential concepts involved in analyzing mathematical functions and their graphical representations. By mastering these concepts, you can gain a deeper understanding of how functions behave, whether they are linear, quadratic, exponential, or more complex.
Identifying Key Features of Graphs
When analyzing a graph, several key characteristics provide valuable information about the function it represents. These features help to define its shape and behavior:
- Intercepts: The points where the graph crosses the x-axis (x-intercepts) and y-axis (y-intercepts). These points provide important information about the function’s values at specific locations.
- Asymptotes: Lines that the graph approaches but never touches. Asymptotes can be vertical, horizontal, or oblique, and they indicate the behavior of the function at extreme values.
- End Behavior: Describes the behavior of the function as the input values approach positive or negative infinity. This helps in understanding the long-term trends of the graph.
Transformations of Functions
Functions can be transformed in various ways, altering their graphs and resulting in changes to their shapes and positions. These transformations include:
- Vertical Shifts: Moving the graph up or down by adding or subtracting a constant to the function.
- Horizontal Shifts: Shifting the graph left or right by modifying the input variable.
- Reflections: Flipping the graph across an axis, such as reflecting it over the x-axis or y-axis.
- Stretching and Compressing: Expanding or contracting the graph vertically or horizontally, which affects the steepness and width of the graph.
By understanding these transformations, you can easily modify a function and predict how its graph will change, making it easier to analyze different types of functions in various contexts.
Handling Systems of Equations Effectively

Systems of equations are a collection of two or more equations that share common variables. Solving these systems is a critical skill, as it involves finding values that satisfy all equations simultaneously. There are several methods for solving systems of equations, and each has its advantages depending on the situation and the complexity of the system.
When solving such problems, it’s important to choose the most efficient method for the given scenario. The most common methods include substitution, elimination, and graphing. Each method has its strengths and can be applied depending on the type of system you’re working with.
Common Methods for Solving Systems

The most frequently used approaches to solve systems of equations are:
- Substitution Method: This method involves solving one equation for one variable and substituting this expression into the other equation. It is particularly effective when one of the equations is easily solvable for a single variable.
- Elimination Method: Also known as the addition or subtraction method, this approach involves adding or subtracting the equations in such a way that one variable cancels out. This method is often useful when the coefficients of one variable are the same or easily manipulated.
- Graphing Method: Involves plotting both equations on a graph and identifying the point(s) where they intersect. This method provides a visual representation but is less precise for non-integer solutions.
Choosing the Right Method
Different systems of equations will lend themselves better to different methods. For example, if one equation is already solved for a variable, the substitution method is typically the fastest. If the coefficients align well for one variable, elimination can be very efficient. Graphing is useful when a visual understanding is required, although it is less precise than algebraic methods.
| Method | When to Use | Advantages | Disadvantages |
|---|---|---|---|
| Substitution | One equation is easy to solve for a single variable | Direct approach, works well with simple equations | Can be tedious with complex expressions |
| Elimination | Coefficients of variables are easy to manipulate | Effective with systems that are balanced | Requires careful manipulation of equations |
| Graphing | Visual representation needed or quick estimation | Provides a clear visual understanding | Less precise for non-integer solutions |
By understanding and applying these methods, solving systems of equations becomes a more systematic and manageable task. It’s important to practice with a variety of systems to gain confidence and familiarity with these approaches.
Practice with Exponents and Radicals

Understanding the operations involving exponents and radicals is fundamental to solving various mathematical expressions. These concepts are not only important in basic arithmetic but are essential in higher-level mathematics as well. By mastering these operations, one can simplify complex expressions, solve equations, and understand the relationships between numbers more effectively.
Exponents refer to repeated multiplication of a number, while radicals are the reverse operation, related to roots. These two concepts often go hand in hand, and it is crucial to be able to switch between them and apply the correct rules. This section focuses on key strategies for working with both exponents and radicals, providing methods to simplify expressions, solve equations, and avoid common mistakes.
Key Rules for Exponents
When working with exponents, several important rules should be remembered to simplify expressions effectively:
- Product Rule: When multiplying numbers with the same base, add the exponents: a^m * a^n = a^(m+n).
- Quotient Rule: When dividing numbers with the same base, subtract the exponents: a^m / a^n = a^(m-n).
- Power Rule: When raising a power to another power, multiply the exponents: (a^m)^n = a^(m*n).
- Zero Exponent: Any number raised to the power of zero is 1: a^0 = 1.
- Negative Exponent: A negative exponent means the reciprocal: a^(-n) = 1/a^n.
Understanding Radicals
Radicals involve finding the root of a number, with the square root being the most common. It is crucial to understand how to simplify radical expressions and perform arithmetic with them. Some important points to remember include:
- Square Roots: The square root of a number a is the number that, when multiplied by itself, gives a. In notation, √a.
- Cube Roots: The cube root of a number a is the number that, when multiplied by itself three times, gives a. In notation, ³√a.
- Simplifying Radicals: To simplify a radical, look for factors that are perfect squares or cubes and factor them out of the radical.
Combining Exponents and Radicals
Exponents and radicals can often be combined in expressions. For example, square roots can be written as exponents: √a = a^(1/2). When simplifying these types of expressions, it is important to apply both exponent rules and radical simplification techniques. Below are some helpful tips:
- Convert between Exponents and Radicals: Recognize that roots can be expressed as fractional exponents: √a = a^(1/2), ³√a = a^(1/3).
- Multiplying Radicals: When multiplying radicals with the same index, multiply the numbers inside the radicals: √a * √b = √(a * b).
- Dividing Radicals: When dividing radicals with the same index, divide the numbers inside the radicals: √a / √b = √(a / b).
By understanding these rules and techniques, solving problems with exponents and radicals becomes easier and more intuitive. Regular practice with these concepts will lead to greater fluency and accuracy in more advanced mathematical tasks.
Trigonometry Applications in Algebra 2
Trigonometry plays a crucial role in understanding and solving various types of mathematical problems. In advanced courses, it bridges the gap between geometric concepts and algebraic expressions, offering new methods for analyzing relationships involving angles, sides, and periodic functions. In this section, we will explore how trigonometric principles are applied within algebraic contexts to solve equations, model real-world situations, and simplify complex expressions.
Solving Trigonometric Equations
One of the key applications of trigonometric functions is solving equations that involve sine, cosine, or tangent. These equations can appear in various forms and typically require knowledge of trigonometric identities and formulas. Common strategies include:
- Using Inverse Functions: Inverse trigonometric functions allow you to find the angle that corresponds to a given trigonometric value. For example, if sin(θ) = 0.5, you can use the inverse sine function to solve for θ.
- Applying Identities: Trigonometric identities, such as the Pythagorean identities, sum and difference formulas, and double-angle identities, are valuable tools for simplifying and solving equations.
- Graphing Methods: Sometimes, graphing the function can help visualize the solution. By plotting the equation and identifying the points of intersection, solutions to trigonometric equations can often be found.
Modeling Real-World Problems with Trigonometry

Trigonometry is frequently used to model and solve problems in fields such as physics, engineering, and architecture. For instance, periodic phenomena such as sound waves, tides, and light patterns can be represented using trigonometric functions. By understanding the relationship between angles and sides, one can create accurate models of these real-world scenarios:
- Modeling Cyclical Behavior: Many natural processes, like seasonal changes or the motion of planets, follow a periodic pattern. Trigonometric functions such as sine and cosine can be used to model these periodic behaviors mathematically.
- Solving for Unknown Angles and Distances: In practical applications such as navigation or engineering, trigonometric relationships allow you to find missing distances or angles in right triangles or other geometric configurations.
- Wave Functions: Trigonometric functions are essential for representing waveforms in physics. For example, the sine and cosine functions are used to describe sound waves, light waves, and electromagnetic waves.
By mastering the connections between algebraic and trigonometric concepts, students can solve a wide range of complex mathematical problems and apply these skills to real-world scenarios. Understanding these applications opens up new perspectives for tackling challenges in advanced mathematics and science fields.
Utilizing Graphing Calculators for Algebra 2
Graphing calculators are powerful tools that help students and professionals visualize mathematical functions and solve equations efficiently. They provide an interactive platform for exploring complex relationships between variables, graphing functions, and performing advanced calculations. By integrating technology into learning, students can gain deeper insights into mathematical concepts and work through problems faster and with greater accuracy.
Graphing Functions and Visualizing Solutions
One of the most common uses of graphing calculators is the ability to graph equations, which allows users to visualize the behavior of different functions. This visual approach can enhance understanding of the function’s properties, such as:
- Intercepts: A graphing calculator can help identify where the function crosses the x-axis (roots) or y-axis, making it easier to solve for unknowns.
- Behavior at Extremes: By examining the graph’s behavior as values approach infinity, students can gain insights into asymptotic behavior or limits.
- Critical Points: The calculator can find maximum or minimum points, offering a quick way to analyze optimization problems.
Solving Equations and Inequalities
Graphing calculators not only help visualize graphs but also provide tools for solving equations and inequalities directly. Features like numerical solvers or root finders allow students to:
- Solve for X: By graphing two functions simultaneously, students can determine the point of intersection, which corresponds to the solution of the equation.
- Graph Inequalities: Many graphing calculators can shade regions of the graph to represent solutions to inequalities, helping students understand solution sets more clearly.
- Perform Numerical Methods: For more complex equations, graphing calculators offer numerical methods like Newton’s method to approximate solutions with precision.
Overall, using graphing calculators can significantly enhance the learning process by providing immediate feedback, facilitating complex calculations, and offering a more hands-on approach to exploring mathematical ideas. By incorporating this technology, students are better equipped to grasp abstract concepts and solve challenging problems more efficiently.