
In this section, we focus on enhancing your understanding of essential mathematical concepts that lay the foundation for more advanced topics. Whether you’re tackling equations or refining problem-solving techniques, this material provides a comprehensive overview to help you build a strong mathematical base.
The goal is to strengthen your skills through targeted exercises that sharpen your ability to manipulate variables, solve for unknowns, and interpret different types of expressions. By honing these abilities, you’ll gain the confidence needed to approach more complex problems with ease.
Through detailed solutions and clear explanations, you’ll be guided step-by-step through common challenges faced by learners. The key to mastering these principles lies in consistent application and understanding the rationale behind each method, rather than simply memorizing formulas.
Chapter 9 Extra Practice Algebra 1 Answers

This section is designed to help reinforce your mathematical knowledge by providing solutions to key exercises. These examples focus on critical skills necessary for solving problems involving variables, equations, and expressions. By working through these examples, you will gain a deeper understanding of the concepts and strategies that make problem-solving more intuitive.
Each solution is broken down into clear, manageable steps to ensure that you can follow the logic and reasoning behind every calculation. These solutions will help you identify patterns, recognize errors, and apply the correct methods to similar problems in the future. Mastery of these techniques is essential for progressing to more advanced topics with confidence.
In addition to solving specific problems, this section offers insights into how to approach mathematical challenges systematically. By practicing with these detailed solutions, you’ll build the skills needed to solve a variety of problems with efficiency and accuracy.
Understanding Key Algebraic Concepts

Grasping the foundational principles of mathematics is crucial for solving complex problems effectively. This section focuses on the core ideas that underpin mathematical reasoning, providing a solid framework for tackling a variety of challenges. Mastery of these concepts equips you with the tools needed to navigate more intricate problems with ease and confidence.
Key ideas such as working with variables, manipulating expressions, and solving equations form the basis for many higher-level topics. Understanding how these components interact is essential for recognizing patterns and making connections between different mathematical techniques. As you develop proficiency in these areas, you’ll be better prepared to approach more advanced topics and apply your knowledge in real-world scenarios.
Through careful examination and problem-solving, you’ll learn how to identify and apply the right methods for each situation. Building a strong understanding of these foundational concepts ensures you have the skills necessary to approach any mathematical challenge logically and efficiently.
Step-by-Step Solution Guide
Breaking down complex problems into simpler, manageable steps is a key strategy for mastering mathematical concepts. This guide provides a detailed walkthrough of each problem, focusing on the logical progression required to find the correct solution. By following the structured approach outlined here, you can develop a deeper understanding of how to approach similar challenges independently.
Identify the Problem and Plan the Solution

The first step in solving any problem is to understand what is being asked. Carefully examine the given information and identify the unknowns. Once you’ve determined the goal, plan the sequence of operations needed to reach the solution. Whether you are solving for a variable or simplifying an expression, outlining the steps ahead of time will help streamline the process.
Execute the Steps and Check the Work
After planning, begin executing each step methodically, ensuring that you follow the correct order of operations. Double-check each calculation and re-evaluate your work as you progress. This not only ensures accuracy but also reinforces your understanding of the techniques involved. If the final result doesn’t match expectations, retrace your steps to find and correct any mistakes.
Common Mistakes to Avoid in Algebra
When solving mathematical problems, it’s easy to make errors that can derail the entire process. Understanding and identifying these common mistakes is essential for improving accuracy and efficiency. Below are some frequent pitfalls students encounter, along with tips on how to avoid them.
- Misapplying the Order of Operations – Failing to follow the correct order of operations often leads to incorrect results. Always remember to perform calculations in the right sequence: parentheses first, followed by exponents, multiplication and division, and finally addition and subtraction.
- Overlooking Negative Signs – A common mistake is forgetting to account for negative signs when simplifying expressions or solving equations. Ensure that you carefully track both positive and negative values throughout the problem.
- Incorrectly Simplifying Fractions – Simplifying fractions too early or inappropriately can lead to incorrect results. Always check that all terms are simplified properly and consistently.
- Forgetting to Distribute Properly – When working with terms inside parentheses, always distribute each term correctly. A common error is neglecting to multiply all terms by the factor outside the parentheses.
- Skipping Steps – Rushing through problems often leads to skipping crucial steps. Taking the time to work through each part of the solution systematically reduces the likelihood of making mistakes.
By being mindful of these errors and practicing careful attention to detail, you can significantly improve your problem-solving skills and avoid common pitfalls in future calculations.
How to Approach Word Problems
Word problems often present challenges because they require both mathematical understanding and the ability to translate real-world situations into mathematical expressions. To solve these types of problems effectively, it’s important to follow a structured approach that allows you to break down the information and identify the key elements.
Start by carefully reading the problem to understand what is being asked. Identify the given information and highlight the key details, such as quantities, relationships, and any conditions or constraints. Next, determine the variables you need to solve for and write down an equation or expression that represents the situation.
After setting up the equation, proceed step by step to solve it, applying appropriate mathematical operations. Always double-check your solution to ensure it answers the original question. If the result doesn’t make sense, go back through the problem and check your steps, making sure that you haven’t overlooked any important details or misinterpreted the information.
Mastering Linear Equations
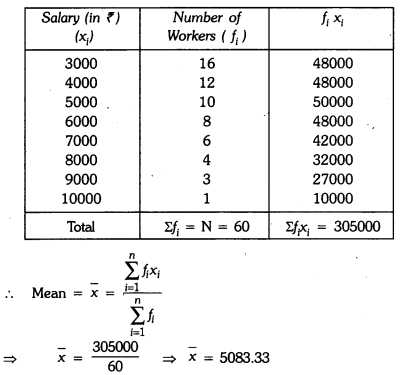
Linear equations form the backbone of many mathematical problems. These equations represent relationships between variables where the highest exponent is one. By mastering the process of solving these equations, you can develop a solid foundation for tackling more complex problems in various areas of mathematics.
To solve linear equations efficiently, it’s essential to isolate the variable. This can be done by performing inverse operations on both sides of the equation, such as addition, subtraction, multiplication, and division. Once the variable is isolated, the solution becomes clear. Below is a breakdown of the general steps involved in solving linear equations:
| Step | Action |
|---|---|
| 1 | Identify the equation and the variable to solve for. |
| 2 | Eliminate any constants from one side of the equation. |
| 3 | Perform inverse operations to isolate the variable. |
| 4 | Check the solution by substituting it back into the original equation. |
By practicing these steps, you will become more efficient at solving equations and gain a deeper understanding of their applications in various scenarios.
Solving Inequalities in Chapter 9
Inequalities are expressions that show the relationship between two values when they are not necessarily equal. Solving these requires a similar approach to solving equations but with extra attention to the direction of the inequality sign. Understanding how to manipulate and solve inequalities is a crucial skill for tackling more complex mathematical challenges.
Key Steps in Solving Inequalities
- Isolate the variable: Just like equations, the goal is to get the variable on one side of the inequality. Use addition, subtraction, multiplication, or division to move terms around.
- Keep the inequality sign correct: When multiplying or dividing by a negative number, the direction of the inequality sign must be flipped.
- Check your solution: Once the variable is isolated, it’s important to check if the solution satisfies the original inequality.
Example Inequalities and Solutions
Consider the following example:
- 3x – 5 > 7
- Step 1: Add 5 to both sides: 3x > 12
- Step 2: Divide both sides by 3: x > 4
By following these steps, you can confidently solve inequalities and understand their solutions in terms of range rather than fixed values.
Tips for Graphing Functions Effectively

Graphing functions is a powerful tool for visualizing mathematical relationships. Whether you’re plotting linear equations or more complex expressions, understanding the key principles behind graphing can help you create accurate and meaningful visual representations. These tips will guide you in graphing functions efficiently and help you avoid common mistakes.
Step-by-Step Approach

- Identify Key Points: Start by determining the intercepts and key values for your function. For example, find where the graph crosses the x-axis (roots) and the y-axis (y-intercept).
- Choose a Range of Values: Select a range of x-values to plot, ensuring they cover the area where the function behaves most interestingly. This helps create a more accurate representation.
- Plot Points Carefully: As you calculate each corresponding y-value, plot each point clearly on the graph. Take time to space the points evenly and check that each is correct.
Graphing Techniques
- Use Symmetry: Many functions, like parabolas or trigonometric graphs, exhibit symmetry. Identifying these patterns can simplify the graphing process and help you plot more points quickly.
- Draw Smooth Curves: Once the points are plotted, connect them with a smooth curve (for non-linear functions) rather than simply drawing lines between points. This creates a more accurate representation of the function’s behavior.
- Label Key Features: Mark the intercepts, maximum or minimum points, and asymptotes on the graph to provide clarity and make it easier to interpret the graph.
By following these strategies, you’ll be able to graph functions more effectively and gain a better understanding of their behavior in different contexts.
Strategies for Factoring Polynomials

Factoring polynomials is a crucial skill that simplifies complex expressions and makes solving equations easier. By breaking down a polynomial into simpler factors, you can often find solutions more quickly. There are several methods available for factoring, depending on the structure of the polynomial. The key is to recognize patterns and apply the appropriate technique systematically.
Here are some strategies to help with factoring polynomials effectively:
| Strategy | When to Use | Example |
|---|---|---|
| Greatest Common Factor (GCF) | When all terms share a common factor. | 3x² + 6x → 3x(x + 2) |
| Difference of Squares | When you have two perfect squares being subtracted. | x² – 9 → (x + 3)(x – 3) |
| Trinomial Factoring | When you have a quadratic trinomial (ax² + bx + c). | x² + 5x + 6 → (x + 2)(x + 3) |
| Factoring by Grouping | When a polynomial has four terms. | x³ + 2x² + 3x + 6 → x²(x + 2) + 3(x + 2) → (x + 2)(x² + 3) |
By using these strategies, you can approach polynomial factoring with greater confidence and efficiency. Understanding which method to apply in different situations is key to mastering this important mathematical concept.
Real-World Applications of Algebra
The concepts learned in mathematical courses have practical applications that extend far beyond the classroom. From everyday problem-solving to complex fields like engineering and economics, mathematical expressions and techniques are integral in a variety of real-life scenarios. By understanding how to manipulate variables and solve equations, you gain the ability to make decisions based on data and predict future outcomes accurately.
One of the most common uses of these skills is in budgeting and finance. Whether it’s managing personal finances or calculating interest rates, the ability to solve equations allows individuals and businesses to make informed financial choices. Similarly, in construction and design, mathematical principles are used to determine dimensions, calculate areas, and estimate material needs, ensuring that projects are completed correctly and efficiently.
Real-world examples of how these concepts are applied:
- Engineering: Engineers use mathematical formulas to design structures, roads, and machinery, ensuring safety and functionality.
- Business: Companies apply mathematical models to analyze data trends, forecast sales, and optimize production processes.
- Technology: In software development and coding, algorithms are built using similar concepts to those learned in mathematical courses, enabling the development of apps and websites.
- Medicine: Health professionals use statistics and equations to track patient data, understand disease patterns, and create treatment plans.
Recognizing these real-world applications underscores the importance of mastering these skills, as they empower you to solve practical problems in nearly every aspect of life.
Using Substitution in Problem Solving

Substitution is a powerful technique for simplifying complex problems, especially when dealing with systems of equations or unknown variables. The method involves replacing one variable with another equivalent expression to make the problem easier to solve. By using substitution, you can break down a problem into smaller, more manageable parts and find the solution step by step.
Here’s how substitution can be applied effectively in problem-solving:
- Identify the Equation to Substitute: Look for an equation where one variable is already isolated or can easily be expressed in terms of another variable.
- Substitute the Expression: Once you’ve identified the expression for one variable, substitute it into the other equation to eliminate one of the variables.
- Simplify the Resulting Equation: After substitution, simplify the equation to solve for the remaining variable.
- Back-Substitute: Once one variable is found, substitute the value back into one of the original equations to solve for the other variable.
For example, if you have a system of equations like:
x + y = 10 2x - y = 3
You can isolate one variable, say y in the first equation:
y = 10 - x
Then substitute this expression for y into the second equation:
2x - (10 - x) = 3
Now, simplify and solve for x. Once you find x, substitute it back into the first equation to find y.
By using substitution, you can efficiently solve systems of equations and other problems involving multiple variables, improving your ability to handle complex mathematical situations.
Improving Problem-Solving Speed
Increasing your ability to solve problems quickly is a valuable skill, especially when faced with time constraints or complex scenarios. The key to improving problem-solving speed lies in practice, familiarity with methods, and developing a strategic approach. By applying the right techniques and enhancing your understanding, you can improve both the accuracy and efficiency of your solutions.
Here are some strategies to enhance your problem-solving speed:
- Master Core Techniques: Familiarize yourself with fundamental methods, such as substitution, elimination, and factoring, so you can quickly identify the best approach for any problem.
- Practice Regularly: The more you practice, the quicker you become at recognizing patterns and solving similar problems. Consistency is key.
- Break Down Complex Problems: When faced with a complicated question, divide it into smaller, more manageable steps. This reduces overwhelm and speeds up your work.
- Work on Mental Math: Strengthening mental calculation skills reduces the need for writing out every step, making the process faster overall.
- Use Shortcuts and Tricks: Familiarize yourself with common shortcuts and tricks, such as factoring simple polynomials or using the distributive property, to solve problems more quickly.
Example of Effective Strategy:
| Step | Action |
|---|---|
| 1 | Read the problem carefully and identify the type of equation. |
| 2 | Choose the most efficient method based on the equation type (e.g., substitution for systems of equations). |
| 3 | Perform calculations mentally or with minimal steps to avoid unnecessary work. |
| 4 | Check your answer quickly to ensure accuracy without reworking the entire process. |
By using these strategies consistently, you’ll improve your ability to solve problems more efficiently, saving time and reducing mistakes.
How to Check Your Answers
Verifying your results is a crucial part of problem-solving, ensuring that your solution is correct and reliable. This process involves going over your work systematically to identify any errors or miscalculations. By checking your work, you can confirm that you haven’t overlooked any details and that your final answer aligns with the given problem.
Here are effective methods for reviewing your solutions:
- Substitute Your Solution Back: One of the simplest ways to check your work is by plugging your solution back into the original equation. If both sides of the equation are equal, the solution is correct.
- Rework the Problem: If you’re uncertain about your solution, solve the problem again from the beginning. A different approach can help identify any steps you might have missed or calculated incorrectly.
- Check Units and Context: Ensure that the solution makes sense within the context of the problem. If you’re solving a word problem, verify that your final answer is reasonable given the scenario.
- Use Estimation: For numerical problems, estimate the answer before solving. This helps you gauge whether your solution is in the correct range and can highlight any major errors.
- Review Each Step: Look at each step in your solution process to ensure that you’ve applied the correct method and followed all logical steps properly.
By adopting these strategies, you can significantly reduce errors and boost your confidence in the correctness of your results.
Importance of Practice in Algebra
Mastering mathematical concepts requires consistent effort and repetition. While understanding the theory is essential, it is the application of learned principles that truly solidifies knowledge. Regularly solving problems allows individuals to enhance their skills, improve problem-solving speed, and gain confidence in their ability to tackle more complex challenges.
Here’s why continuous engagement with mathematical exercises is so valuable:
- Reinforces Learning: The more you engage with various problems, the better you understand the underlying concepts. Practice strengthens your ability to recall and apply formulas and rules effectively.
- Develops Problem-Solving Strategies: Each problem presents a unique challenge, encouraging you to experiment with different approaches. This not only broadens your skill set but also builds a deeper understanding of the problem-solving process.
- Boosts Confidence: As you work through more problems successfully, your confidence grows. This sense of achievement is crucial in tackling even more difficult questions in the future.
- Identifies Areas for Improvement: Regular exercises highlight specific areas where you may need additional focus. Identifying weak points early allows you to address them before they become bigger obstacles.
- Enhances Speed and Accuracy: With repeated practice, you become more efficient at solving problems. Familiarity with the types of questions and their solutions helps improve both speed and accuracy.
Ultimately, the key to proficiency in any subject lies in regular, deliberate practice. Embrace the challenge, and you’ll find your abilities growing with each problem solved.
Time Management for Algebra Practice
Effectively managing your time while solving mathematical problems can significantly enhance your learning experience. By allocating specific time slots for working through exercises and ensuring consistency, you can optimize both your focus and productivity. This method not only helps prevent burnout but also encourages a more strategic approach to mastering concepts.
Setting Realistic Goals
Before diving into any set of exercises, it’s important to define clear, achievable goals. Break down larger tasks into smaller, more manageable segments. For example, aim to solve a set number of problems in a given time frame rather than overwhelming yourself with too much at once. By achieving small wins, you’ll maintain motivation and momentum.
Prioritizing Tasks
Focus on the most challenging topics first. Tackling complex problems when you’re fresh will allow you to apply more focus and energy. Afterward, revisit easier tasks to reinforce your understanding and build confidence. Prioritizing ensures that you’re spending your time on the areas that need it the most, while also making sure that you review and practice consistently.
Incorporating these time management strategies can significantly improve the efficiency of your study sessions. The key is consistency and a balanced approach that prevents frustration while ensuring continuous progress.
Additional Resources for Algebra 1

To enhance your understanding of key mathematical concepts, there are numerous supplementary materials available. These resources provide additional exercises, detailed explanations, and various strategies to further develop your skills. By exploring different platforms and tools, you can strengthen your grasp of the subject and boost your problem-solving abilities.
Online Learning Platforms
- Khan Academy: Offers free, comprehensive tutorials and practice problems covering all aspects of basic mathematics.
- Coursera: Provides structured courses from universities, ideal for those seeking a more formal approach to learning.
- EdX: Similar to Coursera, EdX offers a variety of mathematics courses tailored to different levels of learners.
Interactive Tools and Apps
- Desmos: An online graphing calculator that allows users to visualize mathematical equations and their solutions.
- Photomath: A mobile app that helps solve problems step by step and provides clear explanations of each solution.
- GeoGebra: A dynamic mathematics tool that enables interactive visualizations, helping users better understand geometry and algebra concepts.
Books and Study Guides
- “The Art of Problem Solving” series: A set of books designed to challenge students with higher-level problems while offering clear explanations.
- “Algebra I For Dummies”: A great beginner-friendly book that explains fundamental concepts in a simplified manner.
- “Practice Makes Perfect: Algebra”: A workbook offering hundreds of problems with detailed solutions for those looking to improve their problem-solving skills.
By utilizing these resources, you can approach your studies with confidence and clarity, reinforcing the concepts learned in class and gaining deeper insights into mathematical principles.
Building Confidence in Math Skills
Developing a strong sense of self-assurance in mathematical abilities is essential for mastering complex concepts. Confidence grows when individuals approach challenges with a positive mindset, break down problems into manageable steps, and recognize their progress. This mindset shift can lead to improved performance and a deeper understanding of mathematical principles.
Steps to Boost Confidence
- Start with Basics: Reinforce foundational concepts before moving to more advanced material. Mastery of simple operations provides the necessary confidence to tackle tougher problems.
- Practice Regularly: Consistent practice is key to improvement. Completing exercises and reviewing past mistakes help solidify understanding and increase comfort with various problem types.
- Set Achievable Goals: Break down learning objectives into smaller, attainable tasks. Meeting these small goals provides a sense of accomplishment and encourages continued effort.
- Ask for Help: Don’t hesitate to seek clarification from teachers, peers, or online resources. Discussing problems can help uncover alternative solutions and prevent feelings of frustration.
Overcoming Common Challenges
- Fear of Mistakes: Mistakes are an essential part of the learning process. Embrace them as opportunities to improve and learn new approaches.
- Handling Complex Problems: Break large, intimidating problems into smaller parts. This helps reduce anxiety and makes the solution more approachable.
- Dealing with Setbacks: Understand that progress may be gradual. Reflecting on progress made rather than focusing on setbacks can help maintain a positive outlook.
Helpful Tools to Build Confidence
| Tool | Benefit |
|---|---|
| Online Tutors | Provides personalized explanations and step-by-step guidance for challenging topics. |
| Interactive Apps | Allows hands-on practice with immediate feedback to identify strengths and areas for improvement. |
| Peer Study Groups | Offers a supportive environment for discussing problems and learning from others’ perspectives. |
By consistently applying these strategies, students can foster a growth mindset and build the confidence needed to succeed in math. This approach not only enhances skills but also boosts motivation, leading to long-term success.