
As you approach the upcoming test, it’s essential to develop a clear understanding of the key concepts that will be evaluated. Mastering the fundamentals will not only help you approach questions with confidence but also improve your problem-solving skills. This section focuses on providing the resources and techniques you need to effectively prepare for the challenge ahead.
Building a strong foundation is the first step in tackling mathematical assessments. Focusing on the core principles, such as functions, rates of change, and areas under curves, will enable you to handle a variety of problems with ease. This guide is designed to help you practice and solidify your understanding of these concepts.
To achieve the best results, it’s important to simulate real testing conditions. Working through problems under time constraints helps you become familiar with the structure of questions and enhances your ability to manage time effectively. Whether you are revisiting topics or learning new techniques, consistent practice will lead to improved accuracy and efficiency.
Essential Tips for Math Test Preparation
When preparing for a challenging assessment, it’s important to approach the material with a strategic mindset. Focusing on the core skills and concepts that are most likely to appear in the questions will help you stay organized and avoid feeling overwhelmed. By mastering key areas and refining your problem-solving methods, you can significantly improve your chances of success.
Understand the Key Concepts
Rather than memorizing formulas, focus on understanding the underlying principles that guide each problem. Knowing how to approach different types of questions will allow you to adapt quickly when faced with unfamiliar problems. A strong grasp of functions, rates of change, and area calculations is crucial for navigating more complex scenarios.
Practice Under Time Constraints
Simulate test conditions by working through problems within a set time limit. This not only helps you get used to the pacing of the assessment but also allows you to identify areas where you need to improve. The more you practice under pressure, the more confident and efficient you’ll become when faced with time-sensitive questions.
Understanding Key Mathematical Concepts

To perform well on a challenging test, it’s vital to focus on the core principles that form the foundation of many questions. A solid understanding of these fundamental concepts will not only improve your problem-solving abilities but also help you approach unfamiliar problems with greater confidence. Mastering the essentials provides the framework for tackling complex scenarios effectively.
Key Areas to Focus On
Several core concepts appear repeatedly and are critical for success. Understanding the following areas will ensure you are well-prepared:
- Limits: Understanding the behavior of functions as they approach specific values is fundamental.
- Derivatives: Grasping how quantities change in relation to one another helps solve many real-world problems.
- Integrals: Mastering the calculation of areas under curves or accumulation of quantities is essential.
Strategies for Mastery
To truly master these concepts, here are some strategies:
- Work through problems step by step, ensuring you understand each phase of the solution.
- Focus on understanding the “why” behind each principle rather than just memorizing techniques.
- Revisit challenging topics regularly to reinforce your knowledge and prevent confusion.
How to Tackle Limits and Continuity
Understanding how functions behave as they approach specific points is essential for solving many mathematical problems. Focusing on limits and continuity allows you to analyze and predict function behavior more effectively. By mastering these concepts, you can confidently approach more complex problems that rely on understanding the way values change and how functions interact with each other.
To tackle problems related to limits, it is important to recognize different types of limits, such as finite limits, infinite limits, and one-sided limits. Each requires a specific approach, but all revolve around understanding the function’s behavior near a certain point. Continuity, on the other hand, deals with whether a function has any breaks or jumps at certain points, and is crucial in determining the function’s overall smoothness.
Start by practicing basic limit problems and slowly increase the difficulty. Focus on recognizing patterns, such as when a function approaches a value from the left or right, and use algebraic techniques to simplify expressions. Understanding the relationship between limits and continuity will provide the foundation for more advanced concepts, making it easier to handle problems that involve rates of change or areas under curves.
Mastering Derivatives in Practice

Understanding how quantities change with respect to one another is a key skill for solving many problems. By focusing on the concept of derivatives, you can gain insights into how functions behave and learn to calculate rates of change in various scenarios. Developing a strong foundation in this area allows you to tackle real-world problems and complex mathematical tasks more effectively.
Key Techniques for Mastery
There are several methods for finding derivatives that will be useful across a wide range of problems. Start by mastering the basic rules of differentiation, such as the power rule, product rule, and chain rule. These tools will help you handle more complex expressions and functions.
Common Pitfalls to Avoid
When calculating derivatives, it’s important to watch out for common mistakes. Pay close attention to sign errors, especially when working with negative exponents or complex functions. Another common issue is forgetting to apply the chain rule when differentiating composite functions. Practice regularly to build confidence and accuracy in these calculations.
Integral Calculus: A Step-by-Step Guide

Understanding how to calculate the total accumulation of a quantity over an interval is an essential skill in mathematics. Whether you’re finding areas under curves or solving problems related to motion and growth, integral techniques play a crucial role. This guide will break down the process into manageable steps, making it easier to grasp and apply the concepts effectively.
Step 1: Recognizing the Need for Integration
The first step in solving integration problems is determining when integration is necessary. Look for problems involving the accumulation of quantities, such as finding areas, volumes, or total change over time. These are often key indicators that integration is required.
Step 2: Applying Basic Integration Rules
Once you’ve identified that integration is needed, start with the basic integration rules. These include:
- Power Rule: For any constant (n), the integral of (x^n) is (frac{x^{n+1}}{n+1}).
- Constant Multiple Rule: If a function is multiplied by a constant, pull the constant out of the integral.
- Sum Rule: The integral of a sum of functions is the sum of the integrals.
Step 3: Handling Complex Functions
As you advance, you’ll encounter more complex integrals. In these cases, use techniques such as substitution and integration by parts. These methods allow you to simplify complicated functions and make them easier to integrate.
Step 4: Solving Definite Integrals
When dealing with definite integrals, remember to apply the limits of integration. Once you’ve found the antiderivative, evaluate it at the upper and lower bounds to find the total accumulated value over the specified interval.
Common Pitfalls in Math Assessments
When tackling complex problems during an assessment, it’s easy to make small mistakes that can lead to incorrect answers. These errors often stem from misunderstandings of key concepts, careless calculations, or misapplying rules. Recognizing and avoiding these common pitfalls will help you perform with greater accuracy and confidence.
Frequent Mistakes to Watch Out For
Several issues tend to arise frequently during tests. Being aware of these can help you avoid them and improve your overall performance:
| Common Mistake | How to Avoid It |
|---|---|
| Sign errors in calculations | Carefully check each step for positive and negative signs, especially when dealing with exponents or simplifying expressions. |
| Forgetting to apply rules correctly | Ensure that you understand the rules thoroughly, such as the power rule or product rule, and apply them consistently. |
| Rushing through the steps | Take your time and double-check your work to avoid careless errors. Ensure you don’t skip any steps or misinterpret the problem. |
| Not simplifying expressions before solving | Always simplify your expressions as much as possible before attempting to solve them, which can make the calculations easier and more accurate. |
How to Avoid These Pitfalls
The best way to reduce errors is through consistent practice and careful attention to detail. Before attempting more difficult problems, make sure you’re comfortable with the basic concepts. Taking the time to review your work after solving each problem will also help catch mistakes early.
Building Problem-Solving Confidence
Building confidence in your problem-solving abilities is crucial when facing challenging tasks. It’s not just about knowing the right techniques but also about developing the mindset that allows you to approach problems with a clear strategy and calm assurance. By strengthening your problem-solving skills through consistent practice and focused effort, you can improve both your performance and your confidence.
Strategies for Improving Confidence
There are several techniques you can use to boost your confidence when approaching mathematical problems:
- Start with Simple Problems: Begin with easier problems to build a foundation and gradually increase difficulty as you gain more confidence.
- Break Down Complex Problems: When faced with a complicated problem, break it into smaller, manageable steps. This makes it easier to understand and solve.
- Practice Regularly: Consistent practice helps reinforce concepts and makes you more comfortable when tackling new problems.
Mindset for Success
Adopting the right mindset is essential for problem-solving success. Focus on the process rather than just the outcome, and don’t get discouraged by setbacks. With each problem you solve, you will improve your skills and increase your confidence.
- Embrace challenges as opportunities to learn.
- Stay persistent, even when you encounter difficult problems.
- Review your mistakes and learn from them to avoid similar errors in the future.
Time Management for Your Practice Test
Effective time management is a key factor in performing well under pressure. During an assessment, it’s crucial to balance speed with accuracy, ensuring you have enough time to work through all the questions without feeling rushed. By mastering time management techniques, you can approach each section with clarity and make strategic decisions about how to allocate your time.
Planning Your Approach
Before starting, it’s helpful to outline a plan for managing your time throughout the test. Here are some strategies to consider:
- Divide the Time: Allocate a specific amount of time to each section or question based on its difficulty. This helps ensure you don’t spend too much time on one problem.
- Start with Easier Questions: Begin with the questions you’re most confident about. This will give you a quick sense of accomplishment and help build momentum.
- Leave Difficult Questions for Later: If you encounter a challenging question, move on and come back to it later. This ensures that you don’t lose valuable time on problems that could be more time-consuming.
Using Breaks Effectively

During longer assessments, taking short breaks can help refresh your mind and improve focus. Here’s how to incorporate them:
- After completing a set of questions, take a 1-2 minute break to clear your mind and stretch.
- Use breaks strategically to step back and reassess your approach if you’re feeling stuck.
- Avoid long breaks, as they can disrupt your flow and waste valuable time.
How to Use Graphing Calculators Effectively
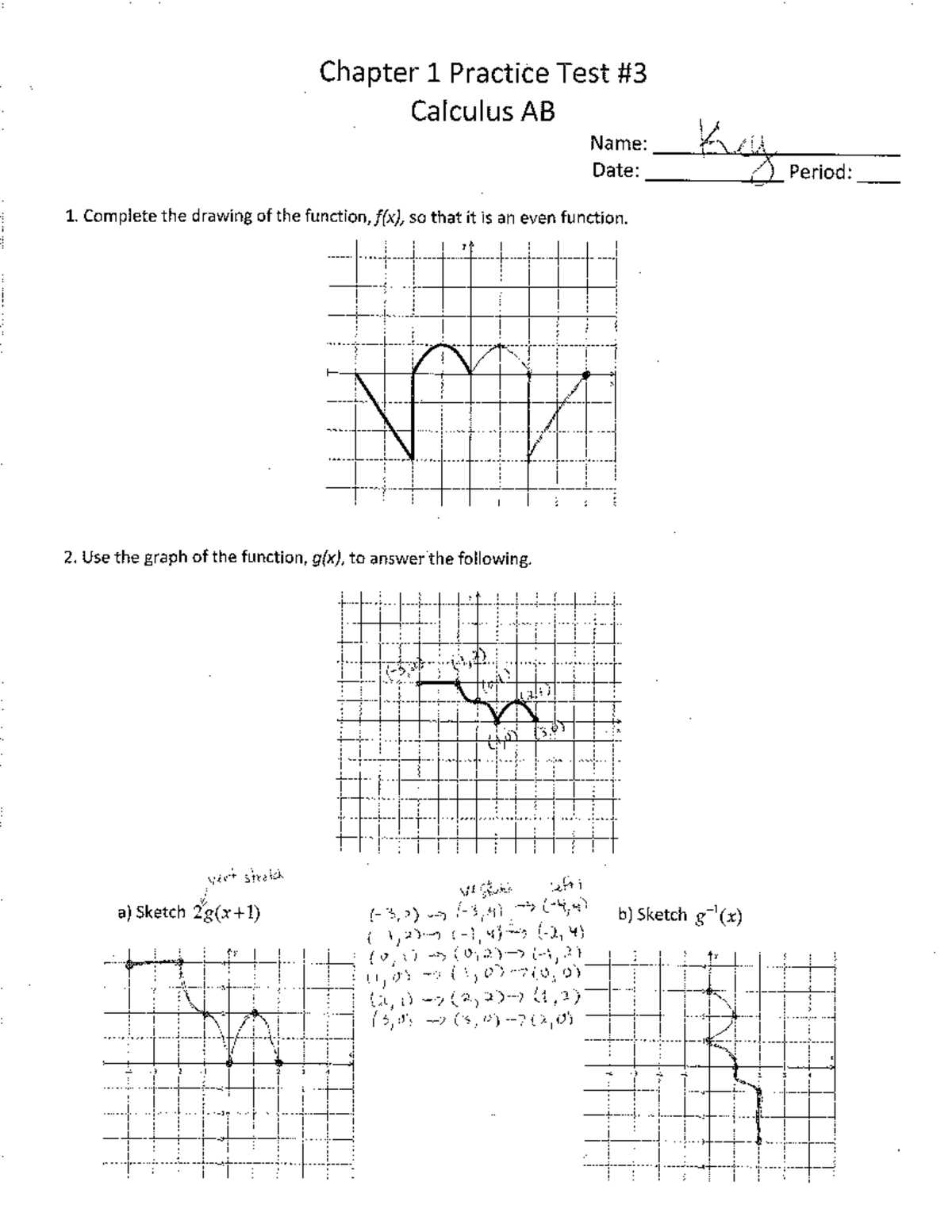
Graphing calculators are powerful tools that can significantly enhance your ability to visualize and solve complex problems. When used correctly, they help you better understand mathematical concepts, check your work, and save time on computations. However, it’s important to use these devices strategically to avoid over-reliance and ensure that you’re still mastering the underlying principles.
Maximizing Functionality
To make the most of your graphing calculator, start by familiarizing yourself with its key functions. These features can be especially useful:
- Graphing Equations: Use the graphing feature to visualize functions and their behavior. This can help you better understand their properties, such as intercepts and asymptotes.
- Table of Values: Input functions to generate a table of values. This is especially useful when you need to evaluate a function at multiple points quickly.
- Zoom and Trace: Adjust the window to view specific areas of a graph and use the trace function to explore points along the curve more accurately.
Practical Tips for Efficient Use
While graphing calculators can speed up problem-solving, using them effectively requires planning and practice. Here are a few tips:
- Start with the Basics: Always start by writing down the problem and attempting to solve it manually before relying on the calculator for verification.
- Verify Results: Use the calculator to check your answers but always ensure that the result aligns with your understanding of the concept.
- Use for Visualization: When dealing with complicated functions or equations, use the calculator’s graphing feature to get a visual representation. This can help you better understand difficult problems and identify potential solutions.
Exploring Real-World Applications of Calculus

Mathematical concepts, once understood, have practical uses that extend far beyond the classroom. The study of rates of change and accumulation allows for solving real-world problems in diverse fields such as engineering, economics, and biology. By applying these concepts, professionals can model complex systems, predict future trends, and optimize solutions to various challenges.
In engineering, for example, these methods are used to design structures and systems that need to withstand specific stresses and forces. In economics, they help to determine the best strategies for maximizing profit or minimizing cost by analyzing changing market conditions. In biology, the same principles are used to model population growth or the spread of diseases.
Understanding how these mathematical tools are applied can provide valuable insights into how they shape the world around us, making them essential for both academic success and real-life problem-solving.
Breaking Down Calculus 1 Practice Problems
When tackling complex problems, breaking them down into manageable parts is key to finding a solution. By approaching each problem step by step, you can simplify even the most challenging tasks. Understanding the core principles behind each type of problem is essential for solving them accurately and efficiently.
Step-by-Step Approach
Start by analyzing the problem and identifying what is being asked. Here’s how you can approach any challenging question:
- Understand the Problem: Read the problem carefully and determine what information is provided and what you need to find.
- Identify the Relevant Concepts: Figure out which mathematical principles or formulas apply to the problem, whether it involves rates of change, areas under curves, or optimizing functions.
- Break it Into Steps: Solve the problem one part at a time. Don’t try to rush through it–tackle each step in sequence to avoid errors.
Common Problem Types
There are several common types of problems that appear regularly in assessments. Understanding how to approach these problems is essential:
- Derivative Problems: Often involve finding the slope of a function or analyzing its behavior. Make sure to apply the correct differentiation rules.
- Integral Problems: Focus on calculating areas under curves or solving accumulation problems. Familiarize yourself with common integration techniques.
How to Study Efficiently for Calculus
Effective study habits can make a significant difference in mastering complex mathematical concepts. Rather than passively reviewing material, active learning techniques can help you retain information and develop problem-solving skills. A structured approach, focusing on understanding key principles and practicing regularly, is essential for success in mastering challenging topics.
To study efficiently, it’s important to break down topics into manageable sections and focus on building a strong foundation. Start by reviewing basic concepts before progressing to more advanced material. Practice problems, timed drills, and group study sessions can enhance understanding and retention.
Additionally, reviewing errors and seeking help when stuck are crucial parts of the learning process. Utilize resources such as textbooks, online tutorials, and peer discussions to reinforce understanding and clarify doubts. Consistency and a focused approach are key to mastering complex material effectively.
Reviewing Trigonometric Functions in Calculus
Trigonometric functions are a crucial component in many areas of mathematics, particularly when analyzing the behavior of curves and modeling real-world phenomena. Mastering these functions allows for the effective handling of various problems involving angles, rotations, and periodic behavior. Understanding the relationships between these functions and their applications is vital for solving more complex problems.
Key Trigonometric Functions

Before diving into more advanced applications, it’s important to familiarize yourself with the fundamental trigonometric functions:
| Function | Formula | Basic Graph Characteristics |
|---|---|---|
| Sine | sin(x) | Periodic with a range of [-1, 1], peaks at 90° and 270° |
| Cosine | cos(x) | Periodic with a range of [-1, 1], peaks at 0° and 180° |
| Tangent | tan(x) | Undefined at 90° and 270°, periodic with asymptotes at these points |
| Cosecant | csc(x) = 1/sin(x) | Periodicity similar to sine, with asymptotes at 0°, 180°, etc. |
| Secant | sec(x) = 1/cos(x) | Periodicity similar to cosine, with asymptotes at 90°, 270°, etc. |
| Cotangent | cot(x) = 1/tan(x) | Periodicity similar to tangent, with asymptotes at 0°, 180°, etc. |
Applications of Trigonometric Functions
These functions are widely used in real-world applications, including physics, engineering, and computer science. In physics, trigonometric functions are often used to model wave behavior, such as sound and light waves. In engineering, they play a role in calculating forces, particularly in the analysis of alternating currents and oscillations. Understanding the properties and behaviors of these functions is essential for applying them effectively in practical situations.
Practical Tips for Memorizing Formulas
Memorizing formulas can be a challenging task, especially when dealing with a large number of equations and mathematical expressions. However, having a strong grasp of essential formulas is crucial for solving problems efficiently. The key to mastering these formulas lies in employing effective memorization techniques that help reinforce your understanding and recall during problem-solving.
One of the most effective strategies is to break down complex formulas into smaller, more manageable parts. By understanding the components and how they relate to each other, you can better remember the structure and application of each equation. Creating mental associations, such as visualizing graphs or linking the formula to a real-world scenario, can also enhance retention.
Another helpful approach is repetition. Regularly writing out formulas, reciting them aloud, and applying them in practice problems can solidify your knowledge. You can also create flashcards with the formula on one side and the application or derivation on the other. This active recall technique is highly effective in reinforcing memory.
Lastly, grouping similar formulas together based on their use or pattern can help you retain them more easily. For example, categorizing formulas related to rates of change, areas, and volumes allows you to remember them by their context. Consistency and frequent practice are the cornerstones of memorizing and applying mathematical formulas effectively.
Understanding Critical Points and Extrema
Critical points and extrema are fundamental concepts in mathematical analysis that are essential for understanding the behavior of functions. These points help determine where a function reaches its highest or lowest values, and they are key to analyzing how a function behaves in different intervals. By identifying critical points, one can gain insights into the function’s increasing or decreasing trends, as well as its concavity and inflection points.
Critical points occur where the first derivative of a function is either zero or undefined. These points are crucial because they often mark locations where the function changes direction or slope, such as peaks, valleys, or flat regions. Analyzing these points can reveal important features, like local maxima or minima, and help sketch the overall shape of the graph.
Identifying Extrema
Extrema refers to the maximum and minimum values of a function, either within a specific range or over the entire domain. Local extrema occur at critical points, where the function attains the highest or lowest value in the immediate neighborhood. To classify these points, the second derivative test is often used. If the second derivative is positive, the point is a local minimum, while a negative value indicates a local maximum. If the second derivative equals zero, further analysis is required to determine the nature of the critical point.
Applying Critical Points in Problem-Solving
Understanding critical points and extrema is essential for solving optimization problems, where the goal is to maximize or minimize a given function. These concepts also play a key role in curve sketching, allowing you to predict where a function changes direction. By effectively identifying and analyzing these points, you can gain a deeper understanding of the function’s behavior and solve a wide range of real-world problems.
Improving Accuracy in Problem Solving
Achieving precision in mathematical problem solving requires careful attention to detail, a solid understanding of concepts, and a methodical approach to each step. By honing certain techniques, you can reduce errors and increase your ability to tackle complex problems with confidence. Whether you’re working through equations, graphs, or optimization tasks, accuracy is key to deriving correct results and achieving success.
One of the most effective ways to enhance accuracy is to break problems down into smaller, manageable parts. This approach allows you to focus on each individual component and avoid overlooking key details. It’s also important to ensure that every step follows logically from the previous one. Skipping steps or rushing through calculations can often lead to mistakes that are hard to catch later on.
Double-Check Your Work
After completing a problem, take time to go back and review your calculations. Even the most experienced problem solvers make occasional errors, so it’s essential to verify each part of your solution. This includes checking for common mistakes such as sign errors, misapplied formulas, or incorrect arithmetic. By developing the habit of reviewing your work, you can catch potential mistakes before finalizing your answers.
Practice with Purpose
Consistent practice is another vital element in improving problem-solving accuracy. However, it’s not just about quantity–it’s about targeted practice. Focus on the areas where you struggle most, and challenge yourself with problems of increasing difficulty. The more you engage with a variety of problem types, the more adept you will become at identifying patterns and applying techniques correctly. Over time, your confidence and precision will improve.
Preparing for Multiple-Choice Questions

Multiple-choice questions often present a unique challenge because they require both understanding of the material and the ability to apply that knowledge quickly. Unlike open-ended problems, where you can show your work step-by-step, multiple-choice questions typically demand precision and efficiency in decision-making. The key to excelling in this format is a solid strategy that allows you to both eliminate incorrect options and zero in on the right answer.
One of the most effective techniques is to first read through the entire question carefully, paying attention to details and ensuring that you fully understand what is being asked. After that, it’s often helpful to mentally solve the problem before reviewing the answer choices. This can prevent you from being misled by seemingly plausible but incorrect options. If you’re unsure of the solution, try to eliminate the most obviously incorrect answers to improve your chances of guessing correctly.
Use Process of Elimination
The process of elimination is an essential strategy for multiple-choice questions. Start by reviewing each answer choice and removing any that are clearly wrong. Often, you can spot common mistakes or misinterpretations in the choices, which can help you narrow down the list. Once you’ve eliminated the choices you’re sure are incorrect, your odds of choosing the right answer increase significantly.
Don’t Rush–Take Your Time
While it’s tempting to answer quickly, rushing through multiple-choice questions can lead to unnecessary mistakes. Take your time to think through each option, double-check your reasoning, and make sure you’re confident in your final choice. Even if you’re unsure of the answer, avoid making snap decisions. Instead, use logical reasoning and any knowledge you have to make an educated guess.