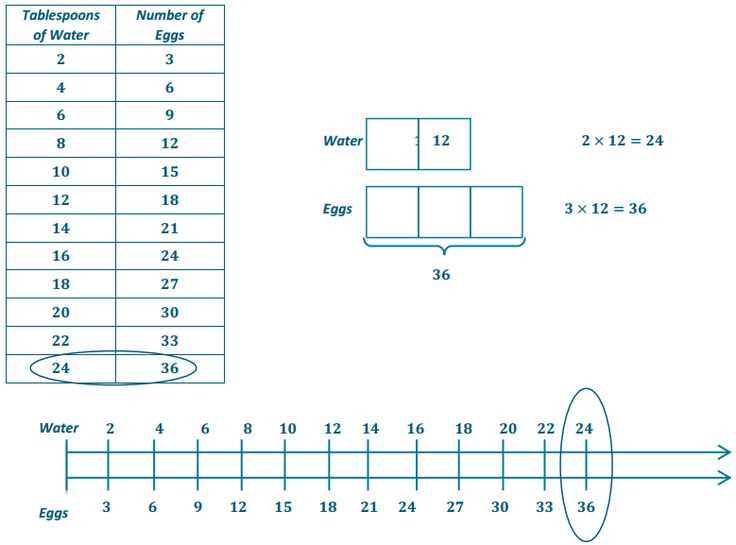
In this section, we explore essential ideas and provide clear methods to tackle the challenges presented in this specific part of the curriculum. Students often face difficulties in grasping complex problems, and having the right approach can make a significant difference in their understanding.
Breaking down problems step by step is vital for mastering the material. By following systematic procedures and practicing common strategies, learners can strengthen their skills and improve their confidence in solving related tasks.
Throughout this guide, focus will be placed on practical techniques and helpful tips that simplify complicated concepts. With the right guidance, students can overcome obstacles and achieve a deeper comprehension of the subject at hand.
Eureka Math Lesson 15 Answers
In this section, we delve into the key solutions and methods necessary for tackling the exercises presented in this unit. The goal is to break down complex problems into manageable steps, allowing students to confidently approach each task and apply the concepts learned.
Through clear explanations and detailed steps, this guide will provide the necessary tools to work through the various challenges. Understanding the underlying principles behind the exercises will ensure a stronger grasp of the material and improve problem-solving skills in future tasks.
By following the outlined steps, learners will develop both the ability and the confidence to complete similar problems independently, ensuring lasting comprehension of the topic.
Overview of Eureka Math Lesson 15
This section focuses on the essential skills and concepts introduced in this part of the curriculum. It provides students with the foundation needed to understand more complex material by simplifying the core ideas into practical steps. The aim is to equip learners with both the knowledge and the techniques necessary to solve various related problems.
Key Topics Covered
The main areas of focus in this section include foundational concepts that are critical for success in subsequent exercises. These core topics help build a deeper understanding that supports further learning.
| Topic | Key Concept | Application |
|---|---|---|
| Basic Operations | Understanding how to apply core principles | Used to solve routine tasks |
| Advanced Techniques | Applying strategies for more complex problems | Enhances accuracy and efficiency |
Building Confidence Through Practice
Repetition and gradual progress are key to mastering the skills needed. By consistently practicing the techniques covered in this section, students will gain the confidence required to tackle more difficult challenges with ease.
Step-by-Step Solutions for Lesson 15
This section provides detailed guidance on how to approach and solve the problems presented in this unit. By breaking down each problem into manageable steps, students can better understand the process and apply the correct methods for finding solutions. The goal is to simplify complex tasks and ensure a clear, logical progression towards the correct answer.
Each step is explained thoroughly, with clear instructions on what actions to take and why they are important. This approach ensures that learners grasp the reasoning behind each solution, helping them to build strong problem-solving skills for similar tasks in the future.
Following this structured method allows for greater clarity, helping students build confidence as they move through each stage of the problem-solving process. By the end of this section, students will have a deeper understanding of how to approach challenges independently, equipped with the skills needed to succeed in subsequent tasks.
Common Challenges in Lesson 15
While tackling the exercises in this section, students often encounter specific obstacles that can hinder their progress. These challenges typically arise from misunderstandings of key concepts or difficulties in applying the appropriate methods to solve problems effectively. Identifying these common struggles early can help students address them and improve their overall understanding.
Typical Struggles Students Face
Some of the most frequent challenges include:
- Difficulty in recognizing patterns and applying them correctly
- Confusion when dealing with multi-step problems
- Misinterpreting word problems and instructions
- Not applying foundational concepts consistently
How to Overcome These Challenges
To help overcome these hurdles, students should:
- Practice breaking down complex problems into smaller, manageable steps
- Review previous exercises to strengthen understanding of basic principles
- Use visual aids, such as diagrams and charts, to clarify tricky concepts
- Seek clarification when instructions or steps seem unclear
By addressing these challenges proactively, students can build the confidence and skills necessary to complete more advanced tasks with ease.
Key Concepts Explained in Lesson 15
This section covers the fundamental ideas that are central to solving the problems presented in this unit. Understanding these core principles is essential for successfully navigating the tasks ahead. By breaking down the concepts and offering clear explanations, students will gain a deeper understanding and be better equipped to approach complex problems.
Understanding Core Principles
The key concepts introduced in this section build on previous material, reinforcing essential skills while introducing new strategies. These include:
- Recognizing relationships between numbers and operations
- Applying formulas to solve multi-step problems
- Understanding how to manipulate variables within equations
- Breaking down complex word problems into simpler components
How to Apply These Concepts
Once these concepts are understood, students can apply them by following a step-by-step approach. This method ensures that all components of a problem are addressed, leading to accurate and reliable solutions. Regular practice of these ideas will help solidify the concepts and build problem-solving confidence.
How to Approach Eureka Math Problems
Successfully tackling problems in this section requires a methodical approach that breaks down each task into manageable steps. Understanding the structure of a problem and identifying the necessary techniques can simplify complex challenges and lead to accurate solutions. Developing a systematic strategy will help students feel more confident when working through similar exercises in the future.
Step-by-Step Strategy
Here’s a general approach to solve problems effectively:
- Read the problem carefully: Understand the context and identify key information.
- Break the problem into smaller parts: Separate the task into manageable steps to avoid feeling overwhelmed.
- Choose the right method: Based on the problem type, select the appropriate technique to apply.
- Double-check calculations: Ensure accuracy at each step to prevent small mistakes from affecting the final result.
- Review the solution: Make sure the answer is reasonable and aligns with the question.
Tips for Success
To maximize success, keep these additional tips in mind:
- Practice regularly to become more comfortable with the techniques.
- Use diagrams or visual aids to clarify complex relationships.
- Don’t hesitate to ask for help when a concept or method is unclear.
- Work through example problems to reinforce your understanding of each concept.
Examples and Solutions for Practice
In this section, we provide a set of example problems along with their solutions to help reinforce the key concepts covered. Working through these examples allows students to apply what they’ve learned in a practical context, strengthening their problem-solving skills and ensuring they can approach similar tasks with confidence.
Example Problems
Below are several example problems that illustrate different types of tasks you may encounter:
- Problem 1: Solve for x in the equation 3x + 7 = 22.
- Problem 2: Simplify the expression 4(2 + 5) – 3.
- Problem 3: Calculate the area of a rectangle with length 6 units and width 8 units.
- Problem 4: Determine the total cost if one item costs $15 and you purchase 4 items.
Step-by-Step Solutions
Here’s how to solve the above problems:
- Solution to Problem 1:
- Start with the equation: 3x + 7 = 22
- Subtract 7 from both sides: 3x = 15
- Divide both sides by 3: x = 5
- Solution to Problem 2:
- Distribute the 4: 4(2 + 5) = 4 × 2 + 4 × 5 = 8 + 20
- Simplify: 8 + 20 – 3 = 25
- Solution to Problem 3:
- Area = length × width = 6 × 8 = 48 square units
- Solution to Problem 4:
- Cost = 4 × $15 = $60
By practicing these examples, students can become more familiar with the steps required to solve similar problems and improve their overall skills.
Understanding Lesson 15 Problem Types
This section explores the various types of problems encountered in this unit, providing a clear understanding of their structure and how to approach them. By familiarizing yourself with the different problem types, you can develop strategies to solve them efficiently and accurately. Each problem requires a distinct method, and recognizing these patterns early will lead to more successful outcomes.
Common Problem Categories
There are several problem types that frequently appear in this section. Each type involves unique concepts and methods, and understanding them is crucial for mastering the material. Below is a breakdown of these common categories:
| Problem Type | Description | Method |
|---|---|---|
| Arithmetic Calculations | Problems that require basic operations such as addition, subtraction, multiplication, and division. | Apply appropriate arithmetic operations in a step-by-step manner. |
| Word Problems | Problems presented in a real-world context requiring interpretation and mathematical application. | Extract key information, set up an equation, and solve. |
| Pattern Recognition | Problems focused on identifying and extending numerical or geometric patterns. | Observe and identify the rule governing the pattern, then extend it. |
| Geometry-Based | Problems related to shapes, measurements, and spatial reasoning. | Apply geometric formulas and principles, such as area and perimeter, to solve. |
Approaching Each Problem Type

For each problem type, it is important to develop a methodical approach. Here are some general strategies:
- For arithmetic calculations, ensure each operation is carried out correctly, one step at a time.
- For word problems, carefully read the problem, identify the given data, and formulate an equation to solve.
- For pattern recognition, look for consistency or repetition in the numbers or shapes, and use this to predict the next element.
- For geometry problems, always recall the relevant formulas and apply them to the given dimensions.
Understanding the different problem types and how to approach them will significantly enhance your ability to solve them efficiently and correctly.
Quick Tips for Solving Lesson 15
In this section, we provide a collection of quick and effective tips that will help you tackle the problems presented in this unit. These tips focus on streamlining the problem-solving process, ensuring that you can approach each task with confidence and clarity. By following these strategies, you can improve both your efficiency and accuracy when solving different types of problems.
Essential Tips for Success
Here are several tips to keep in mind as you work through the exercises:
| Tip | Description |
|---|---|
| Read the Problem Carefully | Always take a moment to understand the problem before jumping into calculations. This ensures you don’t overlook important details. |
| Identify Key Information | Highlight or underline numbers and keywords to identify what is being asked and the data you need to use. |
| Break It Down | Divide the problem into smaller, manageable steps to make it less overwhelming and easier to solve. |
| Check Your Work | After solving the problem, revisit each step to confirm the calculations and reasoning are correct. |
| Practice Regularly | Frequent practice reinforces concepts, making it easier to recall methods and strategies during assessments. |
Using Visual Aids
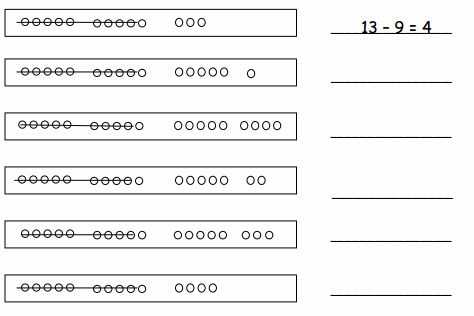
For many problems, using diagrams, number lines, or tables can help visualize relationships and guide you to the correct solution. Drawing out a problem can sometimes reveal patterns or insights that may not be immediately apparent in the text alone.
By applying these tips, you will not only improve your problem-solving skills but also increase your confidence in handling complex tasks.
Strategies for Mastering Eureka Math
Mastering complex problems requires more than just memorizing formulas–it involves understanding the underlying concepts and developing effective strategies to solve various challenges. In this section, we will explore some key approaches that can help students excel in tackling the tasks presented in this unit. With consistent practice and strategic thinking, anyone can improve their proficiency and confidence.
Approach to Problem-Solving
To become proficient in solving the exercises, it’s essential to follow a systematic approach to each problem:
- Understand the Question: Always read the problem thoroughly to identify what is being asked before jumping into calculations.
- Plan the Steps: Break down the problem into smaller parts. This allows you to tackle each segment one at a time, reducing confusion.
- Check for Patterns: Many problems follow recognizable patterns. Look for repeating structures that can simplify the solution process.
- Use Resources: Don’t hesitate to refer to your notes, textbooks, or online resources when you’re unsure about a specific concept.
- Practice Regularly: Consistent practice is key to reinforcing concepts and building the confidence needed to handle more complex problems.
Time Management and Focus
Time management plays a crucial role in mastering this material. Here are a few strategies to manage your study time effectively:
- Set Specific Goals: Break your study sessions into focused blocks of time with clear objectives for each session.
- Practice Timed Tests: Simulate exam conditions by setting a timer to complete problems, helping you improve your time management and focus under pressure.
- Review Mistakes: After completing exercises, take the time to review errors and understand where you went wrong. This will help you avoid repeating the same mistakes.
By incorporating these strategies into your study routine, you’ll be able to develop a deeper understanding of the material, build your problem-solving skills, and increase your chances of mastering the concepts in this unit.
Visual Aids to Help with Lesson 15
Incorporating visual tools into your study routine can significantly improve your understanding and retention of complex concepts. By using diagrams, charts, and other visual aids, you can better visualize relationships and patterns, making it easier to approach and solve problems. In this section, we will discuss some of the most effective visual resources to support learning in this unit.
Types of Visual Aids
There are several types of visual aids that can help simplify and clarify the concepts being taught:
| Visual Aid | Purpose |
|---|---|
| Number Lines | Great for understanding sequences, operations, and relative positioning of numbers. Helps to visualize addition, subtraction, and comparisons. |
| Bar Charts | Ideal for comparing quantities, displaying data, and understanding ratios or percentages. |
| Diagrams | Useful for illustrating geometric shapes, relationships, and transformations. Helps students visualize the problem’s structure. |
| Tables | Organizing information into tables helps to clearly display sets of data and relationships, making them easier to analyze. |
How to Use Visual Aids Effectively
To maximize the benefits of visual tools, it’s essential to use them strategically:
- Refer to visuals regularly: Keep visual aids nearby and reference them while solving problems to reinforce your understanding.
- Draw your own visuals: Whenever possible, try drawing diagrams or charts yourself. This helps reinforce the material and makes the concepts more tangible.
- Combine visuals with written steps: Use visual aids in conjunction with written explanations to create a clearer, more comprehensive solution approach.
By integrating these visual tools into your study approach, you can enhance your problem-solving skills and improve your ability to grasp abstract concepts in this unit.
Common Mistakes to Avoid in Lesson 15
When tackling complex problems, it’s easy to make errors that can hinder progress and understanding. Identifying and avoiding these common pitfalls can help improve accuracy and ensure better problem-solving results. In this section, we will highlight the frequent mistakes students encounter in this unit and offer suggestions on how to avoid them.
Common Errors in Problem-Solving
Here are some typical mistakes to watch out for while working through exercises:
- Misreading the Question: Failing to fully comprehend the problem can lead to incorrect approaches. Always read the instructions carefully and identify key information.
- Skipping Steps: Rushing through the solution process can lead to missed steps. It’s important to break the problem into smaller parts and follow the logical sequence.
- Forgetting to Double-Check: Small mistakes in calculations or reasoning can easily be overlooked. Always take a moment to review your work before finalizing answers.
- Overcomplicating the Problem: Some problems appear more complicated than they really are. Look for simple solutions and avoid unnecessary steps or assumptions.
- Not Using Resources: Many students overlook the value of referring to notes, diagrams, or examples. Make sure to use all available resources to clarify concepts and solve problems effectively.
Strategies to Overcome Mistakes
To prevent these errors, it’s important to adopt certain strategies:
- Practice Active Reading: Before attempting a solution, read through the problem multiple times to ensure you understand what is being asked.
- Break Problems into Small Parts: Tackling complex tasks in smaller, manageable chunks can help you stay organized and avoid missing crucial details.
- Review Your Work: After solving, double-check each step for accuracy. Reviewing ensures that no small mistake has been overlooked.
- Ask for Help: Don’t hesitate to ask a teacher, tutor, or peer for clarification if you’re stuck or confused about any part of the process.
By staying mindful of these common mistakes and applying these strategies, you’ll be better equipped to navigate challenges and enhance your understanding of the material.
Resources for Additional Help
When tackling challenging concepts, having access to additional resources can make a significant difference in mastering the material. Whether it’s extra practice, clarification of complex topics, or seeking guidance on tricky problems, these tools can help you strengthen your understanding. In this section, we’ll explore various options available for further support and learning.
Online Platforms and Tutorials
There are numerous online resources that offer video tutorials, practice exercises, and step-by-step explanations. Some of the most effective platforms include:
- Khan Academy: A comprehensive educational website offering free lessons and practice exercises across various subjects. It breaks down topics into easy-to-understand videos and activities.
- IXL Learning: A personalized learning platform that provides interactive exercises and feedback, allowing students to work through topics at their own pace.
- Coursera: Offering courses and tutorials from universities and institutions, Coursera allows learners to access structured content on a wide variety of subjects.
- Desmos: A digital calculator tool that helps visualize mathematical concepts through interactive graphs and charts, making abstract ideas more accessible.
Study Groups and Peer Assistance
Collaborating with peers can provide insights and explanations that help clarify challenging material. Joining a study group or asking for peer assistance can be invaluable:
- Study Groups: Form or join a study group to discuss problems, exchange ideas, and tackle difficult exercises together. Working with others can help reinforce your understanding.
- Online Forums: Websites like Stack Exchange and Reddit have communities where students can post questions and receive answers from other learners and educators.
- Peer Tutoring: Some schools or learning centers offer peer tutoring programs, where fellow students can help you understand difficult concepts in a more relatable way.
By leveraging these resources, you can supplement your learning and address any challenges you face more effectively, ensuring you’re well-prepared to succeed.
How Lesson 15 Builds on Previous Lessons
The concepts explored in this section are designed to expand upon the foundational ideas introduced earlier in the course. By revisiting key skills and applying them in new contexts, learners can deepen their understanding and strengthen their ability to solve more complex problems. This approach ensures that each new topic feels familiar, yet challenges students to refine their existing knowledge and build on it progressively.
Throughout this section, students will notice how earlier principles are revisited in a way that reinforces both their previous learning and their growth. By working through increasingly difficult problems that rely on prior knowledge, learners can make stronger connections between concepts, improving retention and problem-solving skills. Additionally, the introduction of new techniques often ties back to simpler methods, which makes it easier for students to grasp more advanced material.
In the following parts of this section, key ideas such as basic operations, logical reasoning, and strategic problem-solving techniques are expanded upon. Each concept in this unit will build on the skills practiced in earlier parts of the course, ensuring a smooth transition and continuous development. By recognizing the patterns and relationships between the topics, students are better equipped to tackle more complex challenges and apply their learning with confidence.
Why Lesson 15 is Crucial for Success
The focus of this section plays a vital role in ensuring long-term academic achievement by providing students with the tools to tackle progressively more challenging material. The concepts and strategies introduced here are designed to serve as a cornerstone for understanding more complex ideas in future topics. Without mastering the skills covered, learners may struggle to keep up with subsequent lessons, making it harder to grasp more advanced principles.
Mastering the material in this section is essential because it reinforces critical thinking and problem-solving abilities that will be applied throughout the course. The lessons taught here build confidence in applying learned techniques to unfamiliar problems, setting a strong foundation for success in later units. When students fully engage with the material in this part of the course, they not only solidify their current understanding but also prepare themselves for future challenges, ensuring their academic progression is smooth and steady.
In essence, this section is a key milestone in a student’s learning journey. It ensures that they are not just absorbing information but are also able to apply it effectively in a variety of contexts, laying the groundwork for continued success in both this course and beyond.
Benefits of Using Eureka Math Methods
The approach used in this curriculum emphasizes a deep understanding of concepts, enabling students to build strong problem-solving skills. By focusing on foundational principles, learners gain a better grasp of the material, which enhances their ability to tackle complex challenges later on. The methods prioritize critical thinking, allowing students to connect ideas and apply them in various scenarios, making learning more meaningful and practical.
One key advantage of this approach is that it promotes long-term retention. Rather than memorizing formulas or methods, students are encouraged to understand the reasoning behind each step. This not only helps them perform better in assessments but also equips them to use their knowledge in real-world situations. Additionally, the structured progression of topics ensures that students are well-prepared for more advanced subjects in the future.
Another benefit is the adaptability of the methods. They are designed to be flexible and cater to various learning styles, allowing students to approach the material in ways that suit them best. This personalized learning experience helps students feel more confident and capable, leading to greater academic success.
Teacher and Parent Support for Lesson 15
Support from both educators and parents is essential for a student’s success, especially when learning complex topics. Teachers play a critical role in guiding students through challenging concepts, providing clear explanations, and offering additional practice when necessary. With the right support, students are more likely to stay engaged, grasp difficult ideas, and build confidence in their abilities.
Parents also play an important part in reinforcing what students learn in the classroom. By creating a positive, supportive environment at home, they can help their children develop a deeper understanding of the material. Simple activities like reviewing homework, discussing key concepts, or encouraging students to ask questions can make a significant difference in the learning process.
Collaboration between teachers and parents ensures that students receive consistent support, both inside and outside of school. When both sides work together, they can identify areas where a student might need extra help and provide the necessary resources or strategies to address those challenges. This partnership ultimately promotes a more successful educational experience for the student.