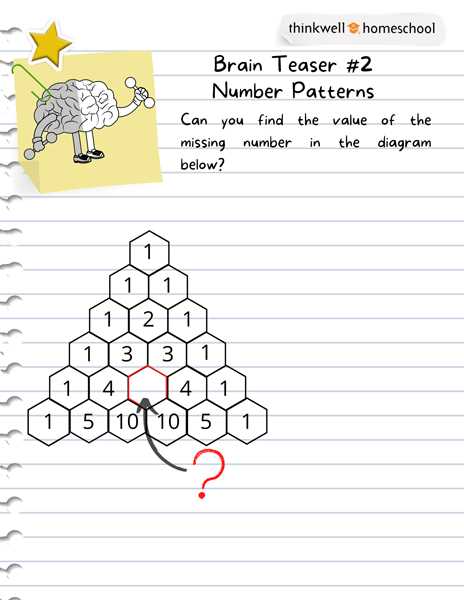
Mastering complex mathematical concepts requires more than just understanding the basics. It involves developing a deeper comprehension of key principles, applying them creatively, and overcoming challenges that often arise in higher-level coursework. By focusing on systematic approaches and targeted practice, students can enhance their problem-solving abilities and achieve success in advanced topics.
In this guide, we explore various methods and resources that help learners tackle difficult questions efficiently. Whether it’s tackling algebraic expressions, geometric proofs, or other advanced exercises, the right strategies can make a significant difference. With step-by-step solutions and helpful tips, students are better equipped to approach complex problems with confidence.
Emphasizing clear logic, structured techniques, and consistent practice can lead to improved understanding and quicker mastery. By avoiding common pitfalls and building strong foundational skills, anyone can excel in more challenging areas of study.
Big Ideas Math Accelerated Answers
When tackling advanced problem-solving tasks in mathematics, having reliable resources and step-by-step solutions is essential. These solutions provide clarity and guide learners through complex equations, ensuring a deeper understanding of the material. By breaking down each problem into manageable steps, students can enhance their logical thinking and problem-solving skills, making challenging topics more accessible.
How Step-by-Step Solutions Aid Learning
Breaking down each mathematical challenge into smaller, understandable components helps students grasp difficult concepts more easily. This approach not only improves comprehension but also fosters confidence when tackling similar problems in the future. Detailed explanations are key to mastering more complex topics, as they reveal the underlying logic behind each solution.
Common Problem Types and Strategies
Advanced coursework often includes a variety of problem types, each requiring a different approach. From algebraic equations to geometric proofs, understanding the best method for each type of problem can significantly speed up the learning process. Below is a table summarizing common problem types and suggested strategies for solving them:
| Problem Type | Suggested Strategy |
|---|---|
| Linear Equations | Use substitution or elimination methods to simplify and solve. |
| Quadratic Equations | Apply factoring, completing the square, or the quadratic formula. |
| Geometric Proofs | Use properties of shapes and theorems to logically prove statements. |
| Word Problems | Translate the problem into an equation and solve step-by-step. |
Overview of Big Ideas Math Program
The educational program designed for advanced learners focuses on providing a comprehensive approach to mastering challenging concepts. It aims to guide students through the learning process with structured lessons, interactive activities, and clear explanations. By incorporating a range of techniques, the program ensures that learners develop a deeper understanding and the ability to apply complex ideas in practical situations.
At its core, the program combines theoretical instruction with hands-on practice, allowing students to engage with material in meaningful ways. It places a strong emphasis on developing problem-solving skills, logical reasoning, and critical thinking, which are essential for success in higher-level studies. The carefully organized content helps learners progress at their own pace while reinforcing key concepts.
Understanding the Accelerated Math Approach
The approach designed for advanced learners focuses on fast-tracking the mastery of complex topics. It allows students to progress more quickly through foundational material and dive deeper into higher-level concepts, often covering topics in less time than traditional curriculums. The key to this method is efficiency: it helps learners grasp essential principles quickly while ensuring a thorough understanding of the core material.
Core Principles of the Approach
This method revolves around building a solid foundation and gradually increasing the complexity of the material. It challenges students to apply critical thinking and solve problems independently, promoting deeper engagement with the subject. By focusing on both speed and comprehension, it aims to develop a balanced skill set, where students can tackle advanced problems confidently and with ease.
Key Benefits for Students
One of the main advantages of this approach is its ability to foster rapid development without sacrificing quality. Students are encouraged to think critically, adapt quickly, and solve complex problems efficiently. This method not only helps in mastering the subject at hand but also prepares learners for future academic challenges. Below is a table outlining the benefits of the approach:
| Benefit | Description |
|---|---|
| Faster Progression | Students advance more quickly through topics, covering more ground in less time. |
| Stronger Problem-Solving Skills | Encourages learners to think critically and independently to solve challenges. |
| Better Conceptual Understanding | Ensures deep comprehension of core ideas and principles. |
| Preparation for Future Success | Prepares students for more advanced academic pursuits and problem-solving tasks. |
How to Use Big Ideas Math Effectively
To achieve success with this advanced learning program, it’s essential to approach the material in a structured and strategic way. The key to mastering complex topics is understanding the logical flow of lessons and applying the techniques consistently. By following a clear plan, students can make the most of the resources available, ensuring a deeper comprehension of the subject and quicker problem-solving skills.
Effective Strategies for Learning
Here are some strategies to help students make the most of their study sessions:
- Break Down Each Concept: Tackle each lesson in manageable sections to ensure full understanding of the core material.
- Use Practice Problems Regularly: Reinforce learning by solving different types of problems to build familiarity and confidence.
- Review Mistakes: Learn from errors by revisiting problems and understanding where mistakes were made.
- Stay Consistent: Set aside regular time for study to ensure continuous progress and avoid overwhelming yourself.
Maximizing Resources
Take full advantage of available tools to improve learning efficiency:
- Interactive Exercises: Use interactive features to apply what you’ve learned and receive instant feedback.
- Teacher or Peer Support: Don’t hesitate to ask for clarification when concepts aren’t fully understood.
- Online Resources: Supplement learning with online tutorials, videos, and forums to gain additional insights and explanations.
Key Concepts in Big Ideas Math
Understanding the core principles behind advanced problem-solving is crucial for success in higher-level coursework. These fundamental concepts provide the foundation for tackling a wide range of challenges and enable students to approach each topic with a deeper understanding. By mastering these key ideas, learners are better equipped to solve complex equations and apply theoretical knowledge in practical scenarios.
Core Principles for Solving Problems
The foundation of any advanced learning program is based on key principles that guide the problem-solving process. Some of these principles include:
- Logical Reasoning: Developing a clear and structured approach to analyzing and solving problems.
- Pattern Recognition: Identifying patterns within problems to simplify complex calculations and make predictions.
- Critical Thinking: Questioning assumptions and exploring different methods to find the most efficient solution.
- Application of Theorems: Using established rules and theorems to solve mathematical challenges and prove solutions.
Building a Strong Foundation in Advanced Topics
As students progress through more advanced topics, a solid understanding of basic principles becomes essential. Key areas of focus include:
- Algebra: Mastering variables, equations, and inequalities to solve for unknowns.
- Geometry: Understanding shapes, angles, and proofs to develop spatial reasoning skills.
- Statistics and Probability: Analyzing data and making predictions using mathematical models.
- Calculus: Exploring concepts of change, motion, and rates to solve problems involving continuous variables.
Mastering Algebra with Big Ideas
Algebra is a critical branch of mathematics that forms the foundation for higher-level topics. Mastering this area requires not only understanding the basic operations and properties but also developing the ability to apply them in complex situations. By using a systematic approach, students can improve their problem-solving skills and gain the confidence needed to handle challenging algebraic expressions.
Key Techniques for Solving Algebraic Equations
To excel in algebra, it’s important to grasp the fundamental techniques that are commonly used to simplify and solve equations. Some essential methods include:
- Simplifying Expressions: Combining like terms and applying the distributive property to make equations more manageable.
- Isolating Variables: Using inverse operations to isolate unknown values and solve for them.
- Factoring: Breaking down complex expressions into simpler factors to make solving easier.
- Using Substitution and Elimination: Applying these methods to solve systems of equations and find solutions.
Building Confidence Through Practice
Practice is the key to becoming proficient in algebra. Regularly solving problems helps reinforce concepts and allows students to apply techniques in different scenarios. Working through a variety of exercises–ranging from simple to complex–builds a stronger grasp of algebraic principles. Repetition, combined with understanding the logic behind each step, leads to mastery.
Exploring Geometry with Accelerated Answers
Geometry is a branch of mathematics that focuses on the properties, measurements, and relationships of shapes and figures. It plays a crucial role in understanding spatial relationships and applying these concepts to solve real-world problems. By mastering geometric principles, students can develop stronger reasoning skills and enhance their ability to approach both theoretical and practical challenges.
When exploring this field, it’s essential to begin with a solid understanding of basic concepts such as points, lines, angles, and shapes. Once these fundamentals are clear, more complex topics, like proofs and transformations, can be tackled with greater confidence. A structured approach to learning ensures that each new concept builds upon the last, creating a strong foundation for more advanced material.
Key Concepts in Geometry
Several key ideas form the backbone of geometry studies. Some of the most important topics include:
- Points, Lines, and Angles: Understanding the basic building blocks of geometric figures and how they interact.
- Triangles and Polygons: Exploring the properties of various shapes and their angles, sides, and relationships.
- Circles and Their Properties: Analyzing the relationship between radius, diameter, and circumference, as well as arc measures and central angles.
- Geometric Proofs: Using logical reasoning to demonstrate the validity of statements based on given conditions.
Applying Geometry to Real-World Problems
One of the greatest benefits of studying geometry is its wide range of applications. Whether it’s in architecture, engineering, or even art, geometric principles are everywhere. By mastering these concepts, students can not only solve abstract problems but also apply their knowledge to practical situations, improving their problem-solving skills and critical thinking abilities.
Important Tips for Solving Problems Faster
Efficient problem-solving is a skill that can be developed with the right strategies. By applying specific techniques and maintaining focus, you can increase your speed while ensuring accuracy. Learning to approach problems with a clear plan and avoiding common pitfalls can significantly enhance your ability to work through challenges quickly and effectively.
Effective Strategies for Speedy Solutions
There are several key strategies that can help you solve problems more quickly:
- Understand the Problem First: Before jumping into calculations, take time to fully understand the problem. Identify what is being asked and the information provided.
- Break It Down: Divide complex problems into smaller, more manageable parts. Solve each section individually to avoid feeling overwhelmed.
- Use Shortcuts and Patterns: Recognize common patterns and mathematical shortcuts that can simplify the problem-solving process.
- Eliminate Unnecessary Steps: Focus on the most efficient method and avoid redundant calculations or steps that do not contribute to the solution.
Building Speed Through Practice
The more problems you solve, the faster you will become. Regular practice helps you identify solutions more quickly and boosts your confidence. Try to challenge yourself with a variety of problems and time yourself to track improvements. Over time, you’ll develop both the speed and accuracy needed to tackle even the most complex challenges with ease.
Challenges Students Face in Accelerated Math
Students in advanced courses often face a unique set of difficulties that require both strong problem-solving skills and effective time management. The complexity and pace of the material can be overwhelming for some learners, especially when the content progresses quickly and demands a deep understanding of previous concepts. As the challenges increase, students must develop strategies to manage the workload and maintain a steady grasp of the subject matter.
One of the most significant challenges is the pressure to keep up with more advanced topics while also ensuring a firm understanding of foundational concepts. As the difficulty level rises, gaps in earlier learning can become more pronounced, making it harder to stay on track. Additionally, the fast-paced nature of accelerated programs may lead to feelings of stress or frustration, particularly if students struggle with a particular concept or problem-solving method.
Common Difficulties in Advanced Courses
Some of the typical challenges that students encounter in these courses include:
- Understanding Complex Concepts: Higher-level topics often require a deeper level of abstract thinking, which can be difficult for students who are still mastering basic principles.
- Time Management: With a faster curriculum, students may struggle to balance their studies, assignments, and extracurricular activities, leading to stress and burnout.
- Overcoming Frustration: When faced with difficult problems, students may experience frustration, especially if they are unable to grasp a concept right away.
- Maintaining Consistency: The rapid pace of advanced courses can sometimes cause students to skip over vital steps, leading to gaps in their understanding.
Strategies for Overcoming These Challenges
To succeed in advanced courses, it is essential to develop strategies that address these challenges. Consistent review of foundational material, seeking help when needed, and breaking down complex problems into simpler steps are just a few methods that can help students stay on track. It’s also important to maintain a balanced approach to studying, setting aside time for regular practice and self-care to avoid burnout.
How Big Ideas Math Enhances Problem-Solving Skills
Developing strong problem-solving abilities is a crucial aspect of any academic pursuit, especially in subjects that require critical thinking and logical reasoning. An effective approach to learning allows students to break down complex challenges into smaller, more manageable steps. By focusing on key strategies and gradually building their knowledge, learners can improve their ability to solve problems efficiently and confidently.
Through a well-structured curriculum, students are encouraged to engage with mathematical concepts in ways that foster a deeper understanding. This not only helps them apply what they’ve learned to different scenarios but also enhances their overall ability to think analytically and solve problems independently.
Key Strategies for Improving Problem-Solving
There are several approaches that can be particularly helpful in strengthening problem-solving skills:
- Step-by-Step Breakdown: Encouraging students to divide problems into smaller, more manageable tasks allows them to focus on one part of the problem at a time, making it easier to find solutions.
- Logical Reasoning: Building a strong foundation in logical thinking helps students recognize patterns, deduce relationships, and apply mathematical rules accurately.
- Real-World Applications: Linking abstract concepts to real-world situations helps students understand the practical value of their skills and motivates them to approach problems with greater confidence.
- Practice with Diverse Problems: Exposing students to a wide range of problem types allows them to develop flexibility in their approach and become more adaptable in different situations.
Developing Critical Thinking through Problem-Solving

As students progress through increasingly challenging material, their problem-solving skills naturally improve. This development isn’t just limited to mathematical concepts–it extends to critical thinking and analytical reasoning in other subjects as well. By consistently practicing and refining these skills, learners become more adept at tackling complex problems and finding effective solutions in various contexts.
Step-by-Step Guide to Solving Complex Problems

When faced with a challenging problem, breaking it down into manageable steps is the key to finding a solution. A structured approach helps you maintain focus, organize your thoughts, and apply the appropriate methods at each stage. By following a systematic process, you can simplify even the most difficult tasks and ensure you don’t overlook crucial details.
Understanding the Problem
The first step in solving any problem is to clearly understand what is being asked. Take time to read through the problem carefully, highlighting important information and identifying what needs to be determined. This initial step sets the foundation for the entire problem-solving process.
- Read the problem carefully: Make sure you know exactly what is being asked.
- Identify key information: Highlight numbers, variables, or conditions provided in the problem.
- Determine what is unknown: Figure out what you need to solve for or find.
Breaking Down the Solution
Once you understand the problem, the next step is to break it into smaller parts. This makes it easier to tackle and reduces the feeling of being overwhelmed by a complex task. Consider these substeps for solving the problem:
- Plan your approach: Decide which method or formula will be most effective.
- Work through each step: Solve one part of the problem at a time, checking your work as you go.
- Verify your solution: After reaching an answer, review the steps and ensure the solution makes sense in the context of the original problem.
By following this methodical process, you can build confidence and improve your ability to solve even the most challenging problems. Regular practice with different types of problems will further enhance your problem-solving skills, making you more adept at handling complexity in the future.
Common Mistakes and How to Avoid Them
When tackling complex tasks, it’s easy to make mistakes that can throw off your entire solution. Recognizing these common errors and understanding how to avoid them is crucial for improving your problem-solving skills. By being mindful of typical pitfalls, you can develop better habits and approach each problem with greater accuracy and efficiency.
Common Errors and Their Solutions

Here are some of the most frequently made mistakes, along with tips on how to prevent them:
| Error | How to Avoid It |
|---|---|
| Misinterpreting the Problem | Always read the problem multiple times and highlight key details before starting. Ensure you understand the goal before proceeding. |
| Skipping Steps | Take your time to work through each part of the problem. Skipping steps may save time initially but can lead to bigger mistakes later. |
| Making Simple Calculation Errors | Double-check your arithmetic, especially when dealing with multiple operations. Use a calculator if necessary to verify results. |
| Forgetting to Check the Final Answer | After solving, always revisit the problem and your solution. Ask yourself if the result makes sense in the context of the question. |
| Overcomplicating the Problem | Keep it simple. Break the problem into smaller, manageable steps and avoid overthinking or adding unnecessary complexity. |
By staying vigilant and following these tips, you can reduce the frequency of errors and improve your problem-solving efficiency. As you gain more experience, you’ll develop a better intuition for identifying potential mistakes early in the process, allowing for quicker and more accurate solutions.
Utilizing Practice Exercises for Better Results

Consistent practice is a crucial component of mastering any skill, especially when it comes to solving complex problems. By engaging in targeted exercises, you can reinforce your understanding, improve accuracy, and develop a deeper mastery of various concepts. The key to success lies in the deliberate practice of problem-solving techniques and the ability to learn from each exercise.
The Benefits of Regular Practice
Practicing regularly helps solidify your knowledge and enhances your ability to apply what you’ve learned under different conditions. Here are some of the key advantages of incorporating practice exercises into your routine:
- Improves retention: Repetition strengthens memory, making it easier to recall key formulas and methods.
- Builds problem-solving speed: The more you practice, the faster and more efficient you become at solving problems.
- Boosts confidence: Completing exercises successfully reinforces your belief in your abilities.
- Identifies weak areas: Practice helps you pinpoint areas where you need more focus and improvement.
Effective Strategies for Practicing
To get the most out of practice exercises, consider the following strategies:
- Start with simpler problems: Begin with basic exercises to build a strong foundation before tackling more difficult tasks.
- Work on variety: Practice a wide range of problems to ensure you are well-rounded in your skills and knowledge.
- Review solutions: After completing each exercise, go over the solution process to identify any mistakes and learn from them.
- Track progress: Keep a log of the problems you’ve solved to see how much you’ve improved over time.
Incorporating these strategies into your study routine will help you optimize your practice sessions and lead to better results over time. With persistence and focus, you’ll find that problem-solving becomes faster, more intuitive, and ultimately more effective.
The Role of Assessments in Accelerated Math
Evaluating progress through assessments plays a vital role in any learning process, especially when it comes to advanced levels of problem-solving. These evaluations provide a clear understanding of a student’s strengths and areas that need improvement, helping both students and educators adjust strategies for more effective learning. Well-structured assessments are designed not only to test knowledge but also to encourage deeper comprehension and critical thinking skills.
Benefits of Assessments

Regular assessments offer multiple benefits that help guide the learning journey. These evaluations are essential for:
- Identifying gaps in understanding: Tests and quizzes highlight specific areas where students may struggle, allowing for targeted interventions.
- Tracking improvement: Assessments serve as a benchmark to measure progress over time, offering insight into how well students are mastering concepts.
- Promoting accountability: Regular checks encourage students to stay on track and take ownership of their learning progress.
- Refining study methods: By analyzing test results, students can adjust their study techniques and focus on the areas that need the most attention.
Effective Assessment Strategies
To ensure that assessments are effective in promoting understanding and growth, the following strategies should be considered:
- Frequent low-stakes assessments: Regular quizzes and short tests help students practice and retain knowledge without the pressure of high-stakes exams.
- Formative assessments: These assessments focus on the learning process rather than the final result, helping students understand their progress and areas for growth.
- Self-assessment: Encouraging students to evaluate their own work fosters self-reflection and helps them become more aware of their strengths and weaknesses.
- Peer assessments: Allowing students to assess each other’s work can enhance understanding by providing different perspectives and promoting collaborative learning.
Incorporating these assessment techniques into the learning process ensures that students are consistently challenged, guided, and supported in their journey toward mastering complex concepts. This approach helps them stay motivated and focused, making it possible to reach higher levels of achievement.
Advantages of Accelerated Math Learning
Advanced learning approaches in mathematics provide students with the opportunity to engage with more complex content at a faster pace. This method encourages deeper understanding and quicker mastery of concepts that would typically take longer to learn. By pushing students to explore topics beyond the usual curriculum, accelerated programs can enhance their problem-solving abilities and critical thinking skills.
Some of the key benefits of this type of learning include:
- Faster mastery of concepts: Students move through material more quickly, allowing them to gain proficiency at an accelerated rate compared to traditional methods.
- Greater academic challenge: More advanced content encourages intellectual growth and fosters a greater love for learning, as students are continually challenged to think critically.
- Increased confidence: Successfully mastering difficult concepts boosts students’ self-esteem and motivation, leading to higher academic achievement.
- Preparedness for future academic pursuits: Accelerated learning prepares students for more advanced coursework in the future, helping them stay ahead of the curve in their educational journey.
- Enhanced problem-solving skills: By tackling complex problems earlier, students develop stronger analytical and logical thinking abilities that will benefit them in other disciplines as well.
With these advantages, students in accelerated learning environments are better equipped to handle advanced academic challenges and pursue higher-level education and careers. As a result, they develop a strong foundation that will support their future success in a variety of fields.
Supporting Students with Math Resources
Providing students with the right tools and resources is crucial for their success in mastering advanced concepts. A well-structured support system not only helps them understand complex topics but also builds their confidence in solving challenging problems. By utilizing a variety of resources, students can engage with material in multiple ways, enhancing their overall learning experience.
Key resources that can support student learning include:
- Interactive Tutorials: Step-by-step guides and video lessons help break down difficult concepts into manageable chunks, making learning more accessible.
- Practice Problems: Providing a wide range of problems for students to solve enables them to apply their knowledge and gain mastery through repetition.
- Study Guides: Comprehensive study guides provide summaries of key concepts, formulas, and strategies, offering students a reference point when preparing for assessments.
- Online Forums and Discussion Groups: Creating spaces where students can ask questions and discuss ideas with peers encourages collaboration and deeper understanding.
- Real-World Applications: Demonstrating how mathematical concepts are used in everyday life can help students connect abstract ideas to tangible outcomes, making learning more meaningful.
By integrating these resources into their study routine, students can develop a well-rounded understanding of the material, improve their problem-solving skills, and feel more prepared for academic challenges. Consistent use of these support tools can make a significant difference in achieving academic success.